Какие свойства у эллипса
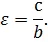
Эллипсом называется геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух заданных точек , и есть величина постоянная , бо́льшая расстояния между этими заданными точками (рис.3.36,а). Это геометрическое определение выражает фокальное свойство эллипса.
Фокальное свойство эллипса
Точки , и называются фокусами эллипса, расстояние между ними — фокусным расстоянием, середина отрезка — центром эллипса, число — длиной большой оси эллипса (соответственно, число — большой полуосью эллипса). Отрезки и , соединяющие произвольную точку эллипса с его фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки эллипса, называется хордой эллипса.
Отношение называется эксцентриситетом эллипса. Из определения следует, что . При , т.е. при , фокусы и , а также центр совпадают, и эллипс является окружностью радиуса (рис.3.36,6).
Геометрическое определение эллипса, выражающее его фокальное свойство, эквивалентно его аналитическому определению — линии, задаваемой каноническим уравнением эллипса:
(3.49)
Действительно, введем прямоугольную систему координат (рис.3.36,в). Центр эллипса примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось или первую ось эллипса), примем за ось абсцисс (положительное направление на ней от точки к точке ); прямую, перпендикулярную фокальной оси и проходящую через центр эллипса (вторую ось эллипса), примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат оказалась правой).
Составим уравнение эллипса, пользуясь его геометрическим определением, выражающим фокальное свойство. В выбранной системе координат определяем координаты фокусов . Для произвольной точки , принадлежащей эллипсу, имеем:
Записывая это равенство в координатной форме, получаем:
Переносим второй радикал в правую часть, возводим обе части уравнения в квадрат и приводим подобные члены:
Разделив на 4, возводим обе части уравнения в квадрат:
Обозначив , получаем . Разделив обе части на , приходим к каноническому уравнению эллипса:
Следовательно, выбранная система координат является канонической.
Если фокусы эллипса совпадают, то эллипс представляет собой окружность (рис.3.36,6), поскольку . В этом случае канонической будет любая прямоугольная система координат с началом в точке , a уравнение является уравнением окружности с центром в точке и радиусом, равным .
Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.49), и только они, принадлежат геометрическому месту точек, называемому эллипсом. Другими словами, аналитическое определение эллипса эквивалентно его геометрическому определению, выражающему фокальное свойство эллипса.
Директориальное свойство эллипса
Директрисами эллипса называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее. При , когда эллипс является окружностью, директрис нет (можно считать, что директрисы бесконечно удалены).
Эллипс с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство эллипса). Здесь и — один из фокусов эллипса и одна из его директрис, расположенные по одну сторону от оси ординат канонической системы координат, т.е. или .
В самом деле, например, для фокуса и директрисы (рис.3.37,6) условие можно записать в координатной форме:
Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению эллипса (3.49). Аналогичные рассуждения можно провести для фокуса и директрисы .
Уравнение эллипса в полярной системе координат
Уравнение эллипса в полярной системе координат (рис.3.37,в и 3.37(2)) имеет вид
где фокальный параметр эллипса.
В самом деле, выберем в качестве полюса полярной системы координат левый фокус эллипса, а в качестве полярной оси — луч (рис.3.37,в). Тогда для произвольной точки , согласно геометрическому определению (фокальному свойству) эллипса, имеем . Выражаем расстояние между точками и (см. пункт 2 замечаний 2.8):
Следовательно, в координатной форме уравнение эллипса имеет вид
Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:
Выражаем полярный радиус и делаем замену :
что и требовалось доказать.
Геометрический смысл коэффициентов в уравнении эллипса
Найдем точки пересечения эллипса (см. рис.3.37,а) с координатными осями (вершины зллипса). Подставляя в уравнение , находим точки пересечения эллипса с осью абсцисс (с фокальной осью): . Следовательно, длина отрезка фокальной оси, заключенного внутри эллипса, равна . Этот отрезок, как отмечено выше, называется большой осью эллипса, а число — большой полуосью эллипса. Подставляя , получаем . Следовательно, длина отрезка второй оси эллипса, заключенного внутри эллипса, равна . Этот отрезок называется малой осью эллипса, а число — малой полуосью эллипса.
Действительно, , причем равенство получается только в случае , когда эллипс является окружностью. Отношение называется коэффициентом сжатия эллипса.
Замечания 3.9
1. Прямые ограничивают на координатной плоскости основной прямоугольник, внутри которого находится эллипс (см. рис.3.37,а).
2. Эллипс можно определить, как геометрическое место точек, получаемое в результате сжатия окружности к ее диаметру.
Действительно, пусть в прямоугольной системе координат уравнение окружности имеет вид . При сжатии к оси абсцисс с коэффициентом координаты произвольной точки , принадлежащей окружности, изменяются по закону
Подставляя в уравнение окружности и , получаем уравнение для координат образа точки :
поскольку . Это каноническое уравнение эллипса.
3. Координатные оси (канонической системы координат) являются осями симметрии эллипса (называются главными осями эллипса), а его центр — центром симметрии.
Действительно, если точка принадлежит эллипсу . то и точки и , симметричные точке относительно координатных осей, также принадлежат тому же эллипсу.
4. Из уравнения эллипса в полярной системе координат (см. рис.3.37,в), выясняется геометрический смысл фокального параметра — это половина длины хорды эллипса, проходящей через его фокус перпендикулярно фокальной оси ( при ).
5. Эксцентриситет характеризует форму эллипса, а именно отличие эллипса от окружности. Чем больше , тем эллипс более вытянут, а чем ближе к нулю, тем ближе эллипс к окружности (рис.3.38,а). Действительно, учитывая, что и , получаем
где — коэффициент сжатия эллипса, . Следовательно, . Чем больше сжат эллипс по сравнению с окружностью, тем меньше коэффициент сжатия и больше эксцентриситет. Для окружности и .
6. Уравнение при определяет эллипс, фокусы которого расположены на оси (рис.3.38,6). Это уравнение сводится к каноническому при помощи переименования координатных осей (3.38).
7. Уравнение определяет эллипс с центром в точке , оси которого параллельны координатным осям (рис.3.38,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36).
При уравнение описывает окружность радиуса с центром в точке .
Параметрическое уравнение эллипса
Параметрическое уравнение эллипса в канонической системе координат имеет вид
Действительно, подставляя эти выражения в уравнение (3.49), приходим к основному тригонометрическому тождеству .
Пример 3.20. Изобразить эллипс в канонической системе координат . Найти полуоси, фокусное расстояние, эксцентриситет, коэффициент сжатия, фокальный параметр, уравнения директрис.
Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — большая полуось, — малая полуось эллипса. Строим основной прямоугольник со сторонами с центром в начале координат (рис.3.39). Учитывая симметричность эллипса, вписываем его в основной прямоугольник. При необходимости определяем координаты некоторых точек эллипса. Например, подставляя в уравнение эллипса, получаем
Следовательно, точки с координатами — принадлежат эллипсу.
Вычисляем коэффициент сжатия ; фокусное расстояние ; эксцентриситет ; фокальный параметр . Составляем уравнения директрис: .
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Источник
Здравствуйте, уважаемые читатели! В статье “Немного геометрии” я упомянул, что есть такие фигуры, как эллипсы. Сегодня хочу рассказать Вам немного подробнее об этом. Кстати, эллипсы имеют широкое распространение в нашей жизни. И здесь Вы найдёте примеры.
Орбиты планет – это огромные эллипсы
Для начала вспомним определение эллипса с точки зрения математики. Итак, эллипс – это геометрическое место точек на плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, постоянна и больше расстояния между фокусами.
Что-то не совсем понятно, да? Чтобы стало яснее, давайте взглянем на картинку ниже. На ней как раз изображён эллипс. Так вот, сумма расстояний от фокусов А и B до кривой, которая и есть эллипс, постоянна, не зависимо от того, какую точку мы возьмём.
Свойство эллипса
Интересным занятием является построение эллипса. Самый простой способ – это взять лист бумаги, две булавки, нить и карандаш. Втыкаете булавки в лист, отмеряете кусок нити так, чтобы он был больше расстояния между булавками и привязываете её концы к обеим булавкам. Затем берёте карандаш, натягиваете им нить и ведёте круговым движением карандашом по бумаге, следя, чтобы нить была всё время натянута. Рисуете половинку эллипса, затем вторую. Вот и готово:
Таким способом раньше садовники делали овальные клумбы. Может, и сейчас где-то делают. 🙂 А вообще, есть специальный чертёжный прибор для рисования эллипсов, который называется эллипсограф. Он состоит из двух ползунков, двигающихся по двум взаимно перпендикулярным осям. Ползунки соединены друг с другом рейкой. На конце рейки есть отверстие для того, чтобы туда можно было вставлять карандаш или ручку. Расстояние между ползунками, а также длину рейки можно изменять. Таким образом получаются эллипсы разной формы. Вот как выглядит одна из разновидностей эллипсографа:
Эллипсограф
У любого эллипса есть свойства. Их много и я не буду перечислять здесь их все, расскажу только об дном, на мой взгляд, самом интересном. Заключается оно вот в чём: если взять любую точку на эллипсе, соединить её с фокусами двумя отрезками, после этого построить биссектрису угла, заключённого между отрезками, затем в вершине угла построить перпендикуляр к биссектрисе, то построенный перпендикуляр будет являться касательной к эллипсу в данной точке:
Свойство эллипса
И что это даёт? – спросите Вы. Так вот, с точки зрения оптики или акустики это свойство имеет очень интересное проявление. Если взять источник света и поместить его в один из фокусов эллиса с внутренней зеркальной поверхностью, то все отражённые лучи сфокусируются в другом фокусе. Из школьного курса оптики мы знаем, что угол падения луча равен углу отражения. А благодаря вышеизложенному свойству эллипса можно наблюдать как раз такую интересную картину. То же самое касается и акустики. Если в фокус эллипса поместить уже источник не света, а звука, то все звуковые волны, отражаясь от внутренней поверхности эллипса сфокусируются во втором фокусе. Если построить помещение, стены которого будут эллипсом и затем поместить двух человек в фокусы этого эллипса, то они будут отлично слышать друг друга, общаясь шёпотом, даже если размеры помещения будут очень большими. Это на самом деле так. 🙂 Вот такое интересное свойство у эллипсов.
А где мы можем встретить эллипсы в нашем окружении? Возьмите любой стакан цилиндрической или конической формы, налейте туда воды, затем немного наклоните стакан – готово. Поверхность воды ограничивается стенками стакана в форме эллипса:
Поверхность воды в стакане – это эллипс
А ещё, эллипсы очень хорошо знакомы всем астрофизикам, ведь любая орбита планеты, вращающейся вокруг своей звезды – это эллипс, причём звезда обязательно находится в одном из фокусов. Так что, эллипс – одна из самых распространённых кривых в мире.
Надеюсь, Вам понравилась статья, и Вы узнали что-то новое и интересное.
Спасибо, что прочитали. Буду благодарен Вашим лайкам, комментариям и подпискам.
Впереди ещё много интересного!
Предыдущая статья
Следующая статья
Источник
Что такое эллипс и фокусное расстояние
Эллипс – это множество точек плоскости, сумма расстояний которых от двух заданных точек, что называются фокусами, есть постоянная величина и равна
.
Обозначим фокусы эллипса
и . Допустим, что расстояние = – фокусное расстояние.
Рис. 1
– фокусы .; , – половина расстояния между фокусами; – большая полуось; – малая полуось.
Теорема:
Фокусное расстояние и полуоси связаны соотношением:
Если точка
находится на пересечении эллипса с вертикальной осью, (теорема Пифагора). Если же точка находится на пересечении его с горизонтальной осью, . Так как по определению сумма – постоянная величина, то приравнивая получается:.
Уравнение эллипса
Уравнение элиппса бывает двух видов:
- Каноническое уравнение эллипса.
- Параметрическое уравнение эллипса.
Сначала рассмотрим каноническое уравнение эллипса:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa
в начале системы координат, а большая ось лежит на абсциссе, то эллипс описывается уравнением:
Если центр эллипсa
смещен в точку с координатами тогда уравнение:
Чтобы получить каноническое уравнение эллипса, разместим
и на оси симметричной к началу координат. Тогда у фокусов будут такие координаты и (см. рис. 2).
Пусть
– произвольная точка эллипса. Обозначим через и – расстояние от точки к фокусам. Согласно с определением эллипса:
(1)
Рис. 2
Подставим в (1)
, и освободимся от иррациональности, подняв обе части к квадрату, получим:
(подносим к квадрату обе части):
,
Обозначим:
, получаем каноническое уравнение эллипса:
(2)
Отметим, что по известному свойству треугольника (сумма двух сторон больше третьей) из
у нас получается . Так как , тогда , и поэтому .
Для построения эллипса обратим внимание, что если точка
принадлежит эллипсу, то есть удовлетворяет уравнение (2), тогда точки тоже удовлетворяют это уравнение: из.
Точки
– расположены симметрично относительно осей координат. Значит, эллипс – фигура, симметричная относительно координатных осей. Поэтому достаточно построить график в первой четверти, а тогда симметрично продолжить его.
Из уравнения (2) находим
, для первой четверти .
Если
, тогда . Если же , тогда . Точки и , а также симметричные с ними , – вершины эллипса, точка – центр эллипса, = большая ось, – малая ось эллипса.
Если
первой четверти, тогда из получается, что при возрастании от к значение падает от к . (рис. 3)
Параметрическое уравнение выглядит так:
Основные свойства эллипса
Рассмотрим основные свойства эллипса, которые необходимы для решения многих задач.
1. Угол между касательной к эллипсу и фокальным радиусом
равен углу между касательной и фокальным радиусом .
2. Уравнение касательной к эллипсу в точке
с координатами :.
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, который соединяет середины отрезков образовавшихся при пересечении прямых и эллипса, всегда проходит через середину (центр) эллипсa. (При помощи данного свойства можно построить эллипс при помощи циркуля и линейка, а также найти центр эллипса).
4. Эволюта эллипсa – это астероида, которая растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами
и у треугольника , тогда выполняется соотношение: =
Эксцентриситет эллипса
Эксентриситет эллипса – это величина отношения межфокусного расстояния к большей оси и после сокращения на обозначается
Значения эксентриситета характеризует степень “сплющенность” эллипса. Если
, тогда – получается круг. Если же , тогда – эллипс превращается в отрезок. В некоторых случаях . Для фокальных радиусов приведём без доказательства такие формулы:
Рис. 3
Эллипс можно построить механическим способом. Из канонического уравнения нужно найти полуоси
и , тогда вычислим – полуфокусное расстояние.
Строим фокусы
и на расстоянии один от другого Концы не растянутой нити длиной закрепляем в точках и . Натягивая остриём карандаша нитку, водим остриём по плоскости таким образом, чтобы нитка скользила по острию. Карандаш при этом опишет полуось. Оттягивая нить в противоположную сторону, начертим вторую половину эллипса.
Примеры решения задач
Задача
Задан эллипс уравнением
и точки . Необходимо:
- убедиться, что точки и лежат на эллипсе;
- найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки к фокусам;
- убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты
точки в левую часть уравнения эллипса:
– точка лежит на эллипсе. Аналогично для :
точка лежит на эллипсе.
2. С канонического
и данного уравнения эллипса выходит: Из равенства получается:
– полуфокусное расстояние. Координаты фокусов и .
3. Найдём фокальные радиусы точки
:
4. Найдём сумму
, что отвечает определению эллипса.
5. Эксцентриситет находится по формуле
.
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
, . Вершины эллипса в точках , , , . Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае больше, чем , то эллипс, который вытянут вдоль оси , находим полуфокусное расстояние .
Фокусы в точках
и . (см. рис. 3)
Рис. 4
Найти оси, вершины и фокусы эллипса
или . Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
, . Откуда находим оси эллипса: , и координаты вершин: , , , . Дальше из формулы:
. Значит, фокусами эллипса есть точки: и . Для построения эллипса отложим на осях и вершины соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении
большей полуосью будет , тогда фокусы эллипса будут расположены на оси и тогда .
Источник
Среди центральных кривых второго порядка особое место занимает эллипс, близкий к окружности, обладающий похожими свойствами, но всё же уникальный и неповторимый.
Определение и элементы эллипса
Множество точек координатной плоскости, для каждой из которых выполняется условие: сумма расстояний до двух заданных точек (фокусов) есть величина постоянная, называется эллипсом.
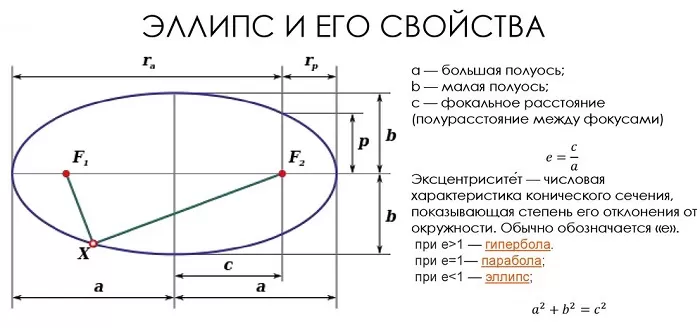
По форме график эллипса представляет замкнутую овальную кривую:
Наиболее простым случаем является расположение линии так, чтобы каждая точка имела симметричную пару относительно начала координат, а координатные оси являлись осями симметрии.
Отрезки осей симметрии, соединяющие две точки эллипса, называются осями. Различаются по размерам (большая и малая), а их половинки, соответственно, считаются полуосями.
Точки эллипса, являющиеся концами осей, называются вершинами.
Расстояния от точки на линии до фокусов получили название фокальных радиусов.
Расстояние между фокусами есть фокальное расстояние.
Отношение фокального расстояния к большей оси называется эксцентриситетом. Это особая характеристика, показывающая вытянутость или сплющенность фигуры.
Основные свойства эллипса
Их несколько:
имеются две оси и один центр симметрии;
при равенстве полуосей линия превращается в окружность;
все точки фигуры лежат внутри прямоугольника со сторонами, равными большой и малой осям эллипса, проходящими через вершины параллельно осям.
Уравнение эллипса
Пусть линия расположена так, чтобы центр симметрии совпадал с началом координат, а оси – с осями координат.
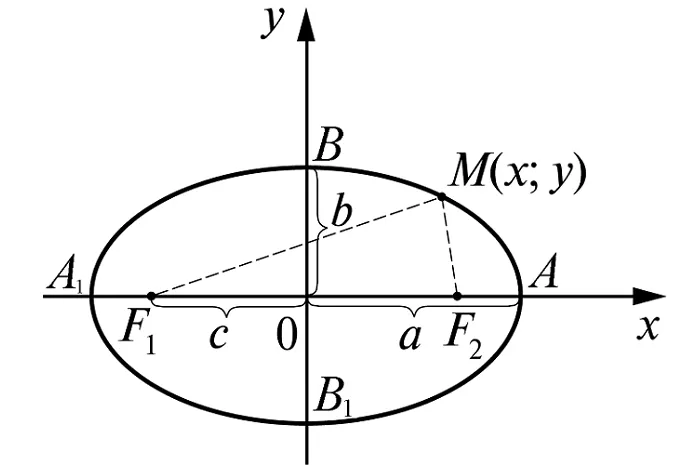
Для составления уравнения достаточно воспользоваться определением, введя обозначение:
а – большая полуось (в наиболее простом виде её располагают вдоль оси Оx) (большая ось, соответственно, равна 2a);
c – половина фокального расстояния;
M(x;y) – произвольная точка линии.
В этом случае фокусы находятся в точках F1(-c;0); F2(c;0)
Согласно определению,
MF1 + MF2 = 2a,
поэтому
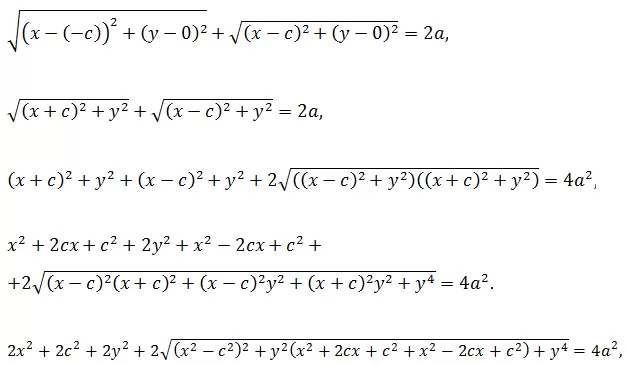
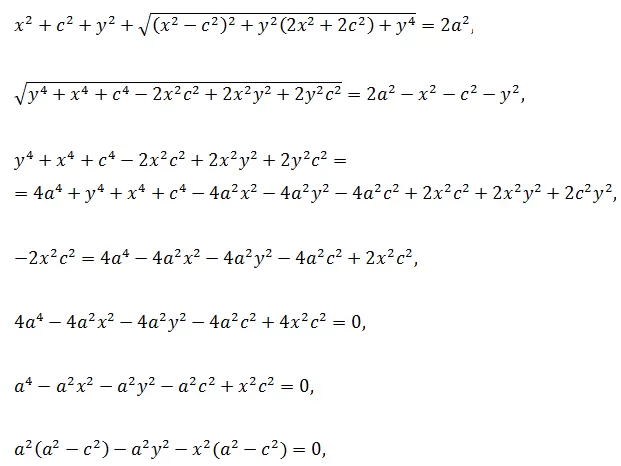
После ввода ещё одного обозначения
b2 = a2 – c2
получается наиболее простой вид уравнения:
a2b2 – a2y2 – x2b2 = 0,
a2b2 = a2y2 + x2b2,
![]()
Параметр b численно равен полуоси, расположенной вдоль Oy (a > b).
В случае (b < a) уравнение не изменится, однако, будет выполняться условие
Такое уравнение называется каноническим, то есть наиболее простым.
Каждое слагаемое в левой части не превосходит единицу.
При возрастании значения lxl уменьшается lyl и наоборот.
В случае (a > b) формула эксцентриситета (ε) принимает вид:
![]()
если b > a, то
![]()
Чем меньше эксцентриситет, тем более сжатым будет эллипс.
Площадь эллипса
Площадь фигуры (овала), ограниченной эллипсом, можно вычислить по формуле:
![]()
a – большая полуось, b – малая.
Площадь сегмента эллипса
Часть эллипса, отсекаемая прямой, называется его сегментом.
![]()
, где
(xo;y0) – крайняя точка сегмента.
Длина дуги эллипса
Длина дуги находится с помощью определённого интеграла по соответствующей формуле при введении параметра:
![]()
Радиус круга, вписанного в эллипс
В отличие от многоугольников, круг, вписанный в эллипс, касается его только в двух точках. Поэтому наименьшее расстояние между точками эллипса (содержащее центр) совпадает с диаметром круга:
r = b.
Радиус круга, описанного вокруг эллипса
Окружность, описанная около эллипса, касается его также только в двух точках. Поэтому наибольшее расстояние между точками эллипса совпадает с диаметром круга:
R = a.
Онлайн калькулятор позволяет по известным параметрам вычислить остальные, найти площадь эллипса или его части, длину дуги всей фигуры или заключённой между двумя заданными точками.
Как построить эллипс
Построение линии удобно выполнять в декартовых координатах в каноническом виде.
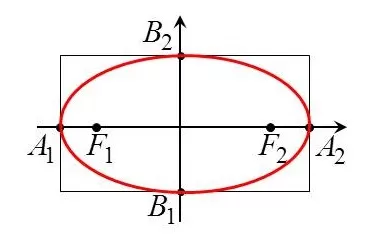
Отмечаются вершины:
![]()
Строится прямоугольник. Для этого проводятся прямые:
![]()
Сглаживая углы, проводится линия по сторонам прямоугольника.
Полученная фигура есть эллипс. По координатам отмечается каждый фокус.
При вращении вокруг любой из осей координат образуется поверхность, которая называется эллипсоид.
Источник
