Какие свойства трапеции являются существенными

В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует знания ее свойств.

Выясним, какими же интересными и полезными для решения задач свойствами обладает трапеция.

После изучения свойства средней линии трапеции можно сформулировать и доказать свойство отрезка, соединяющего середины диагоналей трапеции. Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.

MO – средняя линия треугольника ABC и равна 1/2ВС (рис. 1).

MQ – средняя линия треугольника ABD и равна 1/2АD.

Тогда OQ = MQ – MO, следовательно, OQ = 1/2AD – 1/2BC = 1/2(AD – BC).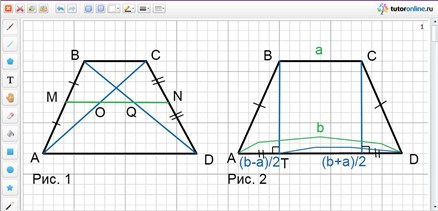

При решении многих задач на трапецию одним из основных приемов является проведение в ней двух высот.

Рассмотрим следующую задачу.

Пусть BT – высота равнобедренной трапеции ABCD с основаниями BC и AD, причем BC = a, AD = b. Найти длины отрезков AT и TD.

Решение.

Решение задачи не вызывает затруднения (рис. 2), но оно позволяет получить свойство высоты равнобедренной трапеции, проведенной из вершины тупого угла: высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.

При изучении свойств трапеции нужно обратить внимание на такое свойство, как подобие. Так, например, диагонали трапеции разбивают ее на четыре треугольника, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики. Это утверждение можно назвать свойством треугольников, на которые разбивается трапеция ее диагоналями. Причем первая часть утверждения доказывается очень легко через признак подобия треугольников по двум углам. Докажем вторую часть утверждения.

Треугольники BOC и COD имеют общую высоту (рис. 3), если принять за их основания отрезки BO и OD. Тогда SBOC/SCOD = BO/OD = k. Следовательно, SCOD = 1/k · SBOC.

Аналогично, треугольники BOC и АОВ имеют общую высоту, если принять за их основания отрезки CO и OA. Тогда SBOC/SAOB = CO/OA = k и SАOВ = 1/k · SBOC.

Из этих двух предложений следует, что SCOD = SАOВ.

Не будем останавливаться на сформулированном утверждении, а найдем связь между площадями треугольников, на которые разбивается трапеция ее диагоналями. Для этого решим следующую задачу.

Пусть точка O – точка пересечения диагоналей трапеции АBCD с основаниями BC и AD. Известно, что площади треугольников BOC и AOD равны соответственно S1 и S2. Найти площадь трапеции.

Так как SCOD = SАOВ, то SАВСD = S1+ S2 + 2SCOD.

Из подобия треугольников BОC и AOD следует, что ВО/OD = √(S₁/S2).

Следовательно,  S₁/SCOD= BO/OD =  √(S₁/S2), а значит SCOD= √(S1 · S2).

Тогда SАВСD = S1 + S2 + 2√(S1 · S2) = (√S1 + √S2)2.

С использованием подобия доказывается и свойство отрезка, проходящего через точку пересечения диагоналей трапеции параллельно основаниям.

Рассмотрим задачу:

Пусть точка O – точка пересечения диагоналей трапеции ABCD с основаниями BC и AD. BC = a, AD = b. Найти длину отрезка PK, проходящего через точку пересечения диагоналей трапеции параллельно основаниям. На какие отрезки делится PK точкой О (рис. 4)?

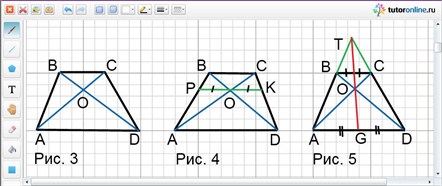
Из подобия треугольников AOD и BOC следует, что АO/OС = AD/BC = b/a.

Из подобия треугольников AOР и ACB следует, что АO/AС = PO/BC = b/(a + b).

Отсюда PO = BC · b / (a + b) = ab/(a + b).

Аналогично, из подобия треугольников DOK и DBC, следует, что OK = ab/(a + b).

Отсюда PO = OK и PK = 2ab/(a + b).

Итак, доказанное свойство можно сформулировать так: отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции.

Следующее свойство четырех точек: в трапеции точка пересечения диагоналей, точка пересечения продолжения боковых сторон, середины оснований трапеции лежат на одной линии.

Треугольники BSC и ASD подобны (рис. 5) и в каждом из них медианы ST и SG делят угол при вершине S на одинаковые части. Следовательно, точки S, T и G лежат на одной прямой.

Точно так же на одной прямой расположены точки T, O и G. Это следует из подобия треугольников BOC и AOD.

Значит, все четыре точки S, T, O и G лежат на одной прямой.

Так же можно найти длину отрезка разбивающего трапецию на две подобных.

Если трапеции ALFD и LBCF подобны (рис. 6), то a/LF = LF/b.

Отсюда LF = √(ab).

Таким образом, отрезок разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому длин оснований.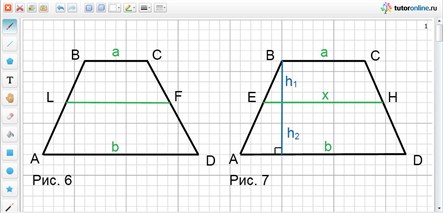

Докажем свойство отрезка, делящего трапецию на две равновеликие.

Пусть площадь трапеции равна S (рис. 7). h1 и h2 – части высоты, а х – длина искомого отрезка.

Тогда S/2 = h1 · (a + x)/2 = h2 · (b + x)/2 и

S = (h1 + h2) · (a + b)/2.

Составим систему

{h1 · (a + x) = h2 · (b + x)
{h1 · (a + x) = (h1 + h2) · (a + b)/2.

Решая данную систему, получим х = √(1/2(а2 + b2)).

Таким образом, длина отрезка, делящего трапецию на две равновеликие, равна√((а2 + b2)/2) (среднему квадратичному длин оснований).

Итак, для трапеции ABCD с основаниями AD и BC (BC = a, AD = b) доказали, что отрезок:

1) MN, соединяющий середины боковых сторон трапеции, параллелен основаниям и равен их полусумме (среднему арифметическому чисел a и b);

2) PK, проходящий через точку пересечения диагоналей трапеции параллельно основаниям, равен
2ab/(a + b) (среднему гармоническому чисел a и b);

3) LF, разбивающий трапецию на две подобные трапеции, имеет длину равную среднему геометрическому чисел a и b, √(ab);

4) EH, делящий трапецию на две равновеликие, имеет длину √((а2 + b2)/2) (среднее квадратичное чисел a и b).

Признак и свойство вписанной и описанной трапеции.

Свойство вписанной трапеции: трапеция может быть вписана в окружность в том и только в том случае, когда она равнобедренная.

Свойства описанной трапеции. Около окружности можно описать трапецию тогда и только тогда, когда сумма длин оснований равна сумме длин боковых сторон.

Полезные следствия того, что в трапецию вписана окружность:

1. Высота описанной трапеции равна двум радиусам вписанной окружности.

2. Боковая сторона описанной трапеции видна из центра вписанной окружности под прямым углом.

Первое очевидно. Для доказательства второго следствия необходимо установить, что угол COD прямой, что так же не составляет большого труда. Зато знание этого следствия позволяет при решении задач использовать прямоугольный треугольник.

Конкретизируем следствия для равнобедренной описанной трапеции:

Высота равнобедренной описанной трапеции есть среднее геометрическое оснований трапеции
h = 2r = √(ab).

Рассмотренные свойства позволят более глубоко познать трапецию и обеспечат успешность в решении задач на применение ее свойств.

 Остались вопросы? Не знаете, как решать задачи на трапецию?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.

Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.

Трапеция и все-все-все

Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.

Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.

В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.

Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.

Свойства диагоналей трапеции

Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.

1. Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2.
2. Перед нам?