Какие свойства точек серединного перпендикуляра к отрезку

Серединный перпендикуляр

Общие сведения

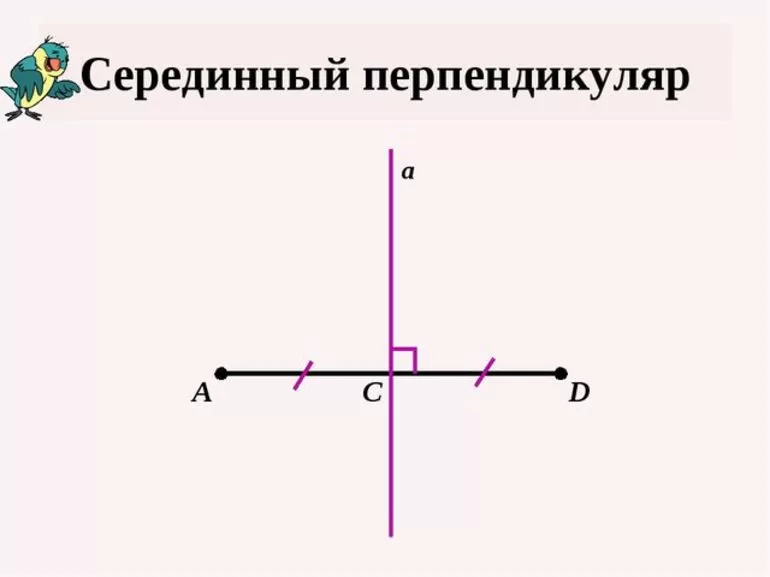
Серединным перпендикуляром отрезка называют прямую, которая проходит под прямым углом через среднюю точку, т. е. середину отрезка. Для полного понимания материала следует остановиться на базовых элементах геометрии.

Общие сведения о серединном перпендикуляре

Точка — единица, при помощи которой строятся прямые, отрезки, лучи и фигуры. Прямая — простая фигура в форме бесконечной линии, состоящей из множества точек, лежащих в одной плоскости. Луч — базовая геометрическая фигура в виде бесконечной линии с одной стороны и точки-ограничителя — с другой. Иными словами, луч имеет начало, но не имеет конца. Отрезок — некоторая часть прямой (луча или другого отрезка), ограниченная двумя точками.

Кроме того, в геометрии серединный перпендикуляр встречается в треугольниках. Из определения можно сделать вывод, что им может быть прямая, отрезок и даже луч.

Аксиомы геометрии Евклида

Евклидовой геометрией называется наука о фигурах на плоскости, основанная на аксиомах и теоремах. Аксиома — базовое утверждение, не требующее доказательства. Оно используется для доказательства каких-либо теорем. Математики выделяют пять аксиом:

Доказательство теоремы

Принадлежности.
Порядка.
Конгруэнтности.
Параллельности прямых.
Непрерывности.

Формулировка первой имеет такой вид: если существует в геометрическом пространстве плоскость, состоящая из множества точек, то через любые из них можно провести только одну прямую. Иными словами, можно взять произвольные две точки и провести через них одну прямую. Чтобы начертить еще одну прямую, следует взять две другие точки.

Следующее утверждение называется аксиомой порядка. Она гласит, что существует точка, которая лежит между двумя другими на прямой. Значение слова “конгруэнтность” не совсем понятно для новичка, однако нужно постепенно привыкать к терминологии. Оно обозначает “равенство”. Третий геометрический факт формулируется таким образом: когда два отрезка или угла конгруэнтны третьему, тогда они равны между собой. Аксиома касается только отрезков и углов.

Чтобы убедиться в ее правильности, нужно разобрать следующий пример: длина первого отрезка составляет 10 см, второго — тоже, а третий равен первому. Необходимо доказать, что они равны между собой. Это делается очень просто:

Вводятся обозначения: первый — MN, второй — OP и третий — RS.
Устанавливаются значения по условию: MN = 10 см, ОР = 10 см, а RS = MN.
Доказательство строится таким образом: MN = RS = 10 (см). Следовательно, отрезки равны, поскольку MN = ОР = RS = 10 (см).

Евклидова геометрия и основные определения базовых понятий

Следует отметить, что данные действия оказались лишними — было потрачено время на понимание простой “истины”. Параллельность прямых является также аксиомой и формулируется таким образом: если существует некоторая прямая на плоскости и точка, не лежащая на ней, то через последнюю можно провести только одну параллельную ей прямую.

И последняя аксиома называется Архимедовой. Ее формулировка имеет такой вид: для произвольных отрезков, лежащих на одной прямой, существует некоторая последовательность базовых элементов (точек), лежащих на одном и другом отрезках, таких, что заданные их части равны между собой. Иными словами, на одной прямой могут быть расположены равные между собой отрезки.

Информация о треугольниках

Треугольником является любая фигура, состоящая из трех вершин (точек) соединенных отрезками (сторонами), причем точки не лежат на одной прямой в одной плоскости. Они классифицируются по такому типу:

Пример решения сложной задачи

Углам.
Сторонам.
Подобию.

В первом случае фигуры делятся на остроугольные, тупоугольные и прямоугольные. Остроугольным называется треугольник, у которого все углы острые (меньше 90 градусов). У тупоугольного — один угол тупой (> 90), а в прямоугольном — один из углов равен 90 градусам. Следует отметить, что сумма градусных мер углов любого треугольника эквивалентна 180.

Когда стороны у треугольника неравны между собой, тогда его называют разносторонним. При равенстве двух боковых сторон он считается равнобедренным, у которого третья сторона — основание. Если все стороны равны, то значит, фигура является равносторонней или правильной.

У треугольника есть еще и другие параметры. Их называют медианой, биссектрисой и высотой. Первый параметр является отрезком, который проводится из любой вершины на среднюю точку стороны. Высота — часть прямой, которая проводится из произвольной вершины и перпендикулярна противоположной стороне. Биссектрисой называется прямая, делящая угол на две равные части.

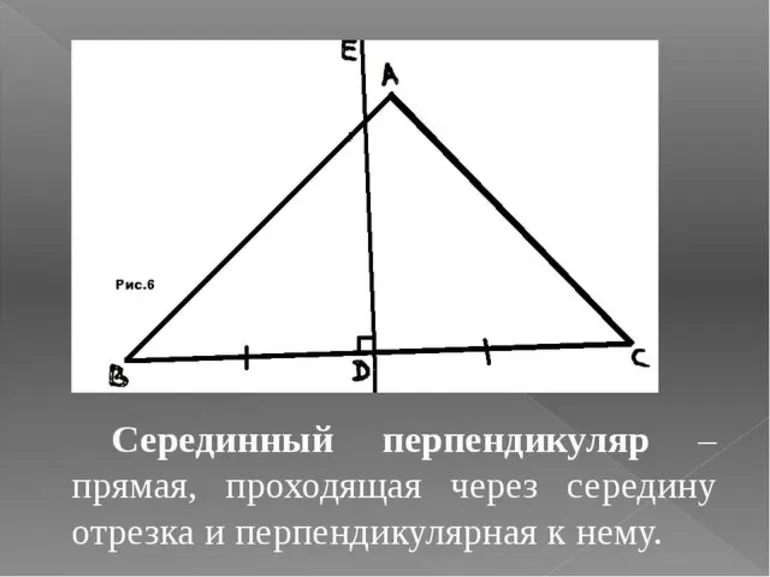
Медиана, высота и биссектриса, проведенные из вершины к основанию, совпадают и эквивалентны серединному перпендикуляру в треугольниках равнобедренного и равностороннего типов. Это очень важно при решении задач. Еще одним признаком, по которому выполняется классификация — подобность треугольников. У них могут быть равными только углы и некоторые стороны. Они отличаются между собой по определенному параметру, который называется коэффициентом подобия. Последний влияет только на размерность сторон. Говорят, что фигуры подобны по определенному признаку (их всего три).

Основные теоремы

Свойства и соотношения

Теорема — гипотеза (предположение), которую нужно доказать. Они применяются для оптимизации расчетов и вычисления отдельных параметров заданной фигуры. Кроме того, существуют следствия, полученные при доказательстве таких научных предположений. Эти аспекты упрощают и автоматизируют вычисления. Например, при вычислении площади треугольника нет необходимости выводить формулу, достаточно воспользоваться уже готовой.

Математики выделяют всего три теоремы о СП, которые могут значительно упростить расчеты. К ним можно отнести следующие:

Прямая.
Обратная.
Пересечение в треугольнике.

Первая теорема называется прямой о СП. Она показывает, каким свойством обладают точки серединного перпендикуляра. Ее формулировка следующая: произвольная точка, которая взятая на перпендикуляре, удалена на равные расстояния от конечных точек отрезка, ограничивающих его на плоскости.

Чертеж к задаче

Для доказательства следует рассмотреть два прямоугольных треугольника с общей вершиной (искомая точка), общей стороной — катетом и равными катетами (по определению). Фигуры равны по одному из признаков равенства треугольников. Следовательно, их гипотенузы (стороны, равенство которых нужно доказать), равны между собой. Первая теорема доказана.

Следующая теорема — обратная: если точка удалена на равные расстояния от концов отрезка, то значит, она лежит на СП. В этом случае следует рассматривать равнобедренный треугольник, вершиной которого она является. Удалена точка на одинаковые расстояния от вершин основания по условию. Следовательно, этот факт доказывает, что полученный треугольник является равнобедренным, а в нем медиана, проведенная к основанию, является биссектрисой и высотой. Значит, она лежит на серединном перпендикуляре. Утверждение доказано.

Следующую теорему нет необходимости доказывать, поскольку известно, что в равнобедренном и равностороннем треугольниках высоты (медианы и биссектрисы) имеют общую точку пересечения. Они являются также и СП. Следовательно, это утверждение справедливо для них.

Важные свойства

Иногда трех теорем недостаточно для решения какой-либо сложной задачи. В этом случае необходимо знать еще и некоторые свойства СП:

Центр описанной окружности вокруг треугольника соответствует точке их пересечения.
Точка, взятая на СП, равноудалена от конечных точек отрезка и образует равнобедренный или равносторонний треугольник.
В треугольниках равнобедренного и равностороннего типов им является высота, медиана и биссектриса.

В первом случае все зависит от типа треугольника. Если он является остроугольным, то центр лежит внутри него. Для тупоугольного — во внешнем пространстве, а в прямоугольном — на середине гипотенузы.

Следует отметить, что есть формулы для его расчета. Если предположить, что существует некоторый произвольный треугольник со сторонами а, b и с. Кроме того, для них выполняется условие a >= b >= c. Исходя из полученных данных, можно записать формулы перпендикуляров (Р), проведенных к определенной стороне:

а: Pa = (2 * а * S) / (a^2 + b^2 – c^2).
b: Pb = (2 * b * S) / (a^2 + b^2 – c^2).
c: Pc = (2 * c * S) / (a^2 – b^2 + c^2).

Иными словами, Р является отношением удвоенного произведения стороны на площадь треугольника к сумме квадратов смежных сторон без квадрата противоположной. Кроме того, справедливы неравенства: Pa >= Pb и Pс >= Pb. Стороны — известные параметры, а вот площадь находится по некоторым соотношениям, которые выглядят следующим образом:

Основание и высоту, проведенную к нему: S = (1/2) * a * Ha = (1/2) * b * Hb = (1/2) * c * Hc.
Через радиус вписанной окружности: S = (1/2) * r * (a + b + c).
Формулу Герона через полупериметр (р) и без него: S = [p * (p – a) * (p – b) * (p – c)]^(1/2) и S = 1/4 * [(a + b + c) * (b + c – a) * (а + c – b) * (a + b – c)]^(1/2).

В основном по таким соотношениям и нужно определить площадь. Полупериметр вычисляется таким образом: р = (а + b + с) / 2.

Бывают задачи, в которых необходимо просто подставить значения в формулу. Они называются простейшими. Однако встречаются и сложные. К ним относятся все виды без некоторых промежуточных параметров фигуры.

Пример решения задачи

В интернете попадаются примеры решения простых задач, а сложные приходится решать самостоятельно, просить помощи у кого-нибудь или покупать на сайтах готовое решение. Для примера нужно решить задание с такими данными:

Понятие о серединном перпендикуляре

Прямоугольник, изображенный на рисунке 1 с диагональю равной d.
Серединный перпендикуляр, проведенный к диагонали прямоугольника.
Точка Е делит сторону на отрезки а и 2а.

Нужно найти: углы, указанные на рисунке, стороны и ОЕ. Кроме того, дополнительные данные можно узнать из чертежа, который используется для решения задачи (рис. 1). К любому заданию нужно делать графическое представление, поскольку оно позволяет избежать ошибок при вычислении

Рисунок 1. Чертеж для решения задачи.

Числовых значений нет, тогда необходимо решать в общем виде. Углы можно найти по такому алгоритму:

Нужно рассмотреть треугольник ВДЕ. Он является равнобедренным, поскольку ОЕ — СП, а диагональ — отрезок. Следовательно, ВЕ = ДЕ = 2а.
Необходимо найти угол ЕВО. Сделать это проблемно. Рекомендуется обратить внимание на треугольник АВЕ.
При помощи тригонометрической функции синуса можно вычислить значение угла АBE: sin(АBE) = a/2а = 0,5. Следовательно, arcsin(0,5) = 30 (градусов).
Угол СВЕ вычисляется следующим образом: 90 – 30 = 60 (градусов).
Следовательно, искомый угол равен 30, поскольку 90 – 30 – 30 = 30.
В равнобедренном треугольнике углы при основании равны между собой: ЕДО = ЕВО = 30 (градусов).

Для нахождения сторон нужно составить уравнение в общем виде, обозначив неизвестную величину АВ литерой “х”. Рассмотрев прямоугольный треугольник АВЕ, по теореме Пифагора можно вычислить АВ: x = [4a^2 + a^2]^(1/2) = a * [5]^(1/2). Следовательно, АВ = a * [5]^(1/2) и ВС = 3а. ОЕ находится по формуле: ОЕ = (2 * 2 * а * S) / (8 * a^2 – d^2). Можно править соотношение таким образом через прямоугольный треугольник ДОЕ: ОЕ = [4 * a^2 – (d^2) / 4]^(1/2).

Таким образом, нахождение серединного перпендикуляра позволяет значительно уменьшить объемы вычислений. Однако для этого нужно знать не только основные теоремы, но и его свойства.

Источник

Серединный перпендикуляр к отрезку

На этом уроке мы узнаем, какими свойствами обладают точки, лежащие на серединном перпендикуляре к отрезку. А также познакомимся со второй замечательной точкой треугольника.

Мы с вами уже знакомы со свойствами точек, лежащих на биссектрисе угла. А точнее, мы знаем, что каждая точка биссектрисы неразвернутого угла равноудалена от его сторон. И знаем, что биссектрисы треугольника пересекаются в одной точке. Эту точку называют замечательной точкой треугольника.

Перейдем к рассмотрению отрезка, его серединного перпендикуляра и свойства точки, которая лежит на серединном перпендикуляре.

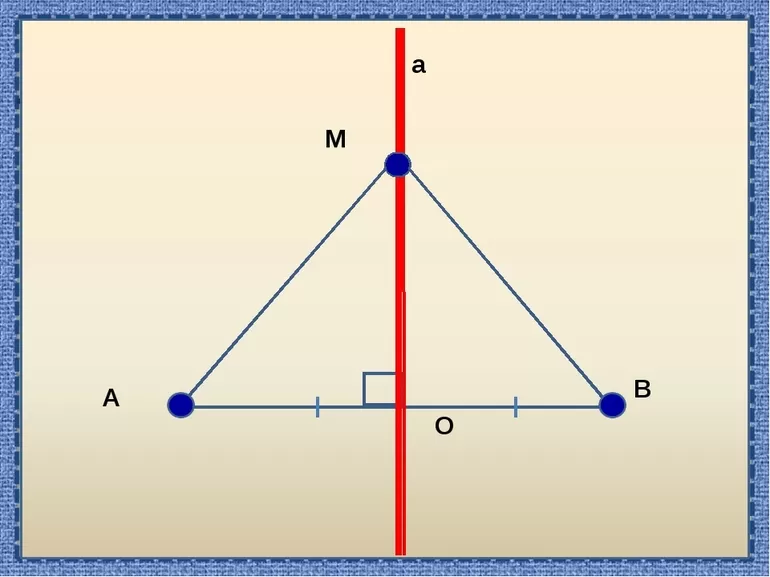
Итак, пусть дан отрезок AB. Прямая l – есть серединный перпендикуляр к отрезку AB.

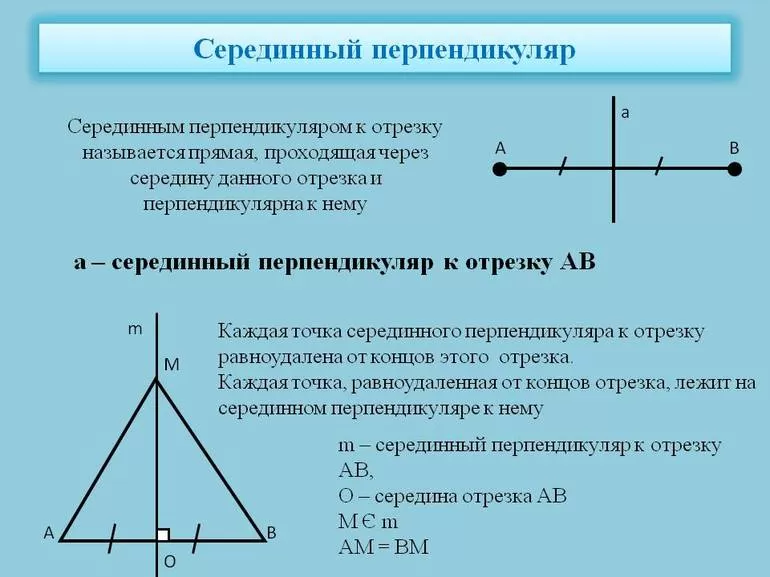
Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

Это означает, что наша прямая l проходит через середину отрезка AB и перпендикулярна ему.

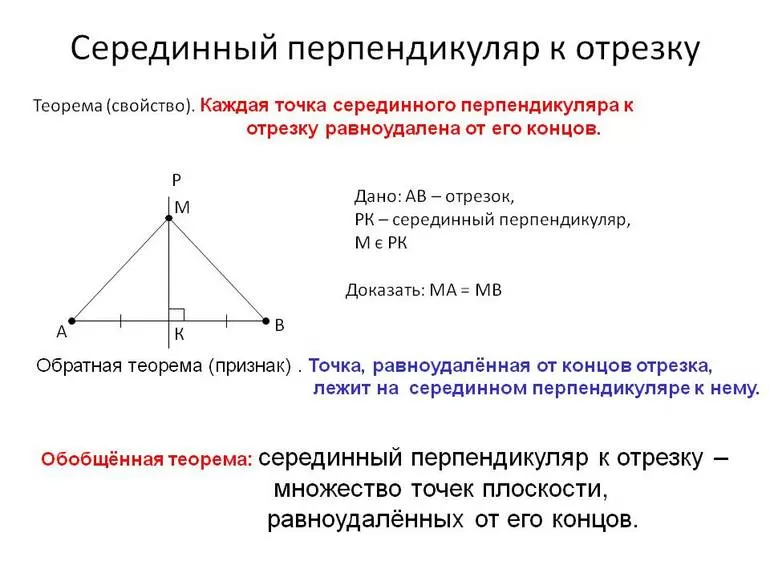
Теорема. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка.

Доказательство.

Докажем, что .

, т.к. середина отрезка по условию.

Рассмотрим и .

,т.к. – общий катет, катеты равны по условию.

равны по двум катетам.

Если точка лежит на серединном перпендикуляре к отрезку, то она равноудалена от концов отрезка.

Теорема доказана.

Обратная теорема. Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

Доказательство.

Докажем, что точка лежит на прямой .

Рассмотрим .

– равнобедренный,

т.к. по условию.

Отрезок – медиана .

– высота

Значит, прямые и совпадают.

Точка лежит на прямой .

Теорема доказана.

Прямую и обратную теоремы можно обобщить. Тогда справедлива теорема: Серединный перпендикуляр к отрезку есть геометрическое место точек, равноудаленных от его концов.

Задача. Серединный перпендикуляр к стороне равнобедренного пересекает сторону в точке . Найдите , если см и периметр см.

Решение.

– по условию.

(см).

Рассмотрим .

– серединный перпендикуляр по условию.

Значит, .

(см).

Ответ: (см).

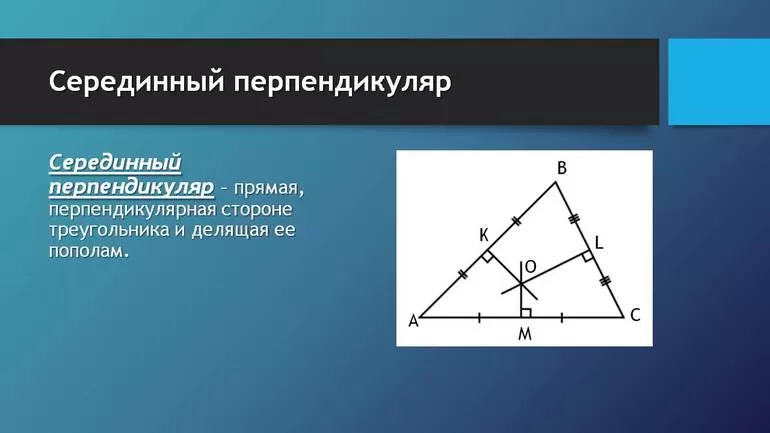
Как вы уже знаете, треугольник состоит из трех отрезков, значит, в нем можно провести три серединных перпендикуляра. Оказывается, эти перпендикуляры пересекаются в одной точке. Эту точку называют второй замечательной точкой треугольника.

Следствие. Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

Следовательно, все три серединных перпендикуляра , и к сторонам пересекаются в точке .

Таким образом, точка – точка пересечения трех серединных перпендикуляров .

Что и требовалось доказать.

Повторим главное:

На этом уроке мы узнали, какими свойствами обладают точки, лежащие на серединном перпендикуляре к отрезку. А именно, каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему. А также узнали, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. И это есть вторая замечательная точка треугольника.

Источник

Холодова Оксана Евгеньевна, учитель математики МАОУ СОШ №19 5 класс, 2016

План-конспект урока по ФГОС в 5 классе «Серединный перпендикуляр»

Холодова Оксана Евгеньевна

учитель математики

МАОУ СОШ №19

Мытищинский район

Учебник для 5 класса общеобразовательных учреждений:

“Математика”, Зубарева И.И., Мордкович А.Г. – М.: Мнемозина, 2015

Цель урока: ввести понятие серединного перпендикуляра, свойства точек, лежащих на серединном перпендикуляре.

Цели:

– обучающие: формировать навыки построения геометрических чертежей с помощью линейки и чертёжного треугольника.

-развивающие: развивать внимание, мышление, самостоятельность;

-воспитательные: воспитывать умение работать в коллективе, самостоятельность, дисциплинированность;

Задачи урока:

Личностные:

Развивать критичность мышления, способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.

Предметные:

Учиться проводить логические обоснования, доказательство математических утверждений, овладение геометрическим языком, уметь использовать его для описания предметов окружающего мира, развивать пространственные представления и изобразительные умения, приобретать навыки геометрических построений.

Метапредметные:

Учиться видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни, уметь осуществлять деятельность, направленную на решение задач исследовательского характера.

Тип урока: объяснение нового материала с применением технологии проблемного обучения, ЭОР.

Формы работы учащихся: фронтальная, коллективная, работа в парах, групповая, индивидуальная.

Необходимое оборудование: компьютер, мультимедийный проектор, линейка, угольник, мел, раздаточный материал.

Структура и ход урока:

Технологическая карта урока

Этапы урока

Задачи этапа

УУД

1. Организационный момент

Создать благоприятный психологический настрой на работу

Личностные: самоопределение.

Регулятивные: целеполагание.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками.

2.Целеполагание и мотивация

Обеспечение мотивации учения детьми, принятие ими целей урока.

Регулятивные: целеполагание.

Коммуникативные: постановка вопросов.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические – формулирование проблемы.

3. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии.

Актуализация опорных знаний и способов действий.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстником.

Познавательные: логические – анализ объектов с целью познания его свойств.

4. Усвоение новых знаний и способов усвоения

Обеспечение восприятия, осмысления и первичного запоминания детьми изученной темы.

Коммуникативные: постановка вопросов, инициативное сотрудничество.

Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство.

Регулятивные: планирование, прогнозирование.

5.Первичное закрепление

Установление правильности и осознанности изучения темы.

Выявление пробелов первичного осмысления изученного материала, коррекция выявленных пробелов, обеспечение закрепления в памяти детей знаний и способов действий, которые им необходимы для самостоятельной работы по новому материалу.

Регулятивные: контроль, оценка, коррекция.

Познавательные: умение структуризировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Коммуникативные: управление поведением партнера, контроль, коррекция, оценка действий партнера.

6. Организация первичного контроля

Выявление качества и уровня усвоения знаний и способов действий, а также выявление недостатков в знаниях и способах действий, установление причин выявленных недостатков.

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения;

Личностные: самоопределение.

7. Подведение итогов урока.

Дать качественную оценку работы класса и отдельных обучаемых

Регулятивные: оценка-осознание уровня и качества усвоения; контроль

8. Информация о домашнем задании

Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.

9. Рефлексия

Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе.

Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли;

Познавательные: рефлексия.

Ход урока:

1. Организационный момент .

Учитель. Добрый день ребята.

Я рада приветствовать вас сегодня на нашем уроке. Надеюсь, что на уроке нас ждёт и успех и радость, и мы, работая в коллективе, покажем свою одарённость. Будьте внимательны в течение урока, думайте, спрашивайте, предлагайте, к истине будем идти вместе.

(Слайд 1)

Эпиграфом к нашему уроку будут эти строки: “ Учиться можно только весело! Чтобы переваривать знания, надо поглощать их с аппетитом. Анатоль Франс…”. Что значит, поглощать с аппетитом? Сегодня, изучая новую тему, мы не сделаем таких великих открытий, как например – Пифагор, но значимые для себя открытия вы совершите обязательно. Для этого надо быть настойчивым и внимательным.

У каждого из вас на столе лежит оценочный лист, в котором вы в течение урока будете оценивать свою работу.

Считал устно

(0-3)

Фронтальный опрос

(0-3)

Практическая работа

(0-3)

Задание

(0-3)

Активность на уроке

(0-3)

Всего баллов

13-15 баллов -5,

9-12 баллов – 4.

оценка

Рефлексия

Откройте тетради, запишите число. Какой самый главный навык в математике? (счет)

Чтобы определить тему, а потом и цели урока, выполним устные вычисления. Но устные вычисления необычные. В них заключено слово, определяющее нашу тему. У вас на столах разноцветные карточки-сигналы. Если ответ неправильный, поднимаем красную карточку, если правильный – зелёную.

2. Устная работа. (Слайд 2)

53-46 (Н) 52+28 (К) 4*9-34 (Л) 27:9+2 (И) 16*2-32 (Д)

60:4-48:4 (Я) (28+26):6 (Е)

Дети устно решают примеры, и в таблице появляется геометрический термин: ПЕРПЕНДИКУЛЯР

—- Оцените свою устную работу (0-3 балла) —-

Итак, определили наше ключевое слово, определяющее часть нашей темы. Но перпендикуляр необычный, какой мы с вами научились строить. А для того, чтобы узнать, какой перпендикуляр, выполним небольшое задание.

-Начертите в тетради любой отрезок и разделите его пополам. Поставьте точку О. Как называется эта точка? (середина отрезка) А теперь соотнесем слово середина со словом перпендикуляр. Какой получится перпендикуляр? (серединный)

Читайте также: Какие свойства у льда

Запишите тему урока. Сегодня на уроке мы продолжим изучать геометрические фигуры: вспомним то, что вы уже знаете, познакомимся с новым понятием и свойством, а так же потренируемся решать задачи. Какие инструменты нам сегодня понадобятся? (угольник, линейка) Сформулируем цели нашего урока относительно темы. (обучающиеся определяют)

(слайд 3) Цели нашего урока: ввести понятие серединного перпендикуляра к отрезку; рассмотреть свойство серединного перпендикуляра; учиться применять известные знания, анализировать, обобщать. (прикрепить на доске)

3. Актуализация опорных знаний. (фронтальный опрос) (Слайд 4)

Какие геометрические фигуры вы видите на слайде? (Прямые, отрезки, и точки)

Сколько здесь прямых? (Две)

Назовите их. (AB и NR)

Можно ли их назвать иначе? (BA и RN)

Назовите отрезок.(CF или FC)

А теперь попробуем сравнить отрезки CF и AB. С помощью чего это можно сделать? (С помощью линейки)

Как? (Измерить длины отрезков и сравнить их друг с другом)

А если у нас нет линейки? (Циркулем)

Как? (Измерить длину одного отрезка, затем приложить циркуль к другому и сравнить с его длиной)

Итак, когда же отрезки будут равны? (Когда у них будет одинаковая длина)

А если у нас нет не только линейки, но и циркуля? Как можно сравнить длины отрезков?

(Существует следующий способ. Для него потребуется прозрачная плёнка и маркер. Накладываем плёнку на один из отрезков и рисуем на ней маркером этот отрезок. Затем накладываем плёнку на другой отрезок, стараясь совместить эти отрезки).

Когда же отрезки будут равны? (Когда они совпадут)

Итак, когда два отрезка будут равны друг другу? (Когда у них будут одинаковые длины или они совпадут при наложении друг на друга)

(Слайд 5) Какой угол видите на рисунке? Назовите его. Сколько градусов составляет прямой угол?

(Слайд 6) Что вы видит на рисунке? Какие прямые называются перпендикулярными? Как узнать, что прямые перпендикулярны?

(Слайд 7) Как построить перпендикулярные прямые с помощью угольника?

(Слайд 8) Как построить перпендикулярные прямые с помощью транспортира?

(Слайд 9) Назовите по рисунку перпендикулярные прямые? Как узнать, что они перпендикулярны?

(Слайд 10) Приведите пример из окружающей вас обстановки, где будут присутствовать перпендикулярные прямые?

—— Поставьте баллы в оценочный лист – фронтальный опрос. (0-3 балла) ———-

4. Изучение новой темы.

(Слайд 11) Ребята, возьмите листочки. Начертите любой отрезок. Отметьте концы отрезка жирными точками.

Перегните лист так, чтобы чертеж был сверху, и точки А и В совместились. Что произошло с отрезком.

Линия перегиба – называется серединным перпендикуляром. Попробуйте сформулировать, что же такое серединный перпендикуляр?

(Слайд 12)

Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.

(Слайд 13)

Назовите на каком рисунке изображён серединный перпендикуляр? Почему?

(Слайд 14)Подумайте, какая буква алфавита содержит серединный перпендикуляр?

(Слайд 15) Физминутка. (видео)

(Слайд 16)

А как же построим серединный перпендикуляр с помощью угольника? (обсуждение).

Строим в тетради и на доске.

(Слайд 17) Отметьте т.М на серединном перпендикуляре. Соедините её с концами отрезка.

Сравните отрезки АМ и ВМ. Какой мы сделаем вывод? (т.М находится на одинаковом расстоянии от концов отрезка)

5. Решение задач (применение полученных знаний). (10 мин)

Практическая работа. Учитель делит класс на группы.

Выдаёт группам задание. (Приложение 1) Помогает сравнить и скорректировать определения. Помогает скорректировать полученные свойства. (Наблюдает за работой каждого учащегося, задаёт проблемные вопросы: «Как разделить отрезок пополам?», «Как приложить треугольник для построения перпендикулярной прямой?» и т. д., оказывает помощь учащимся, испытывающим затруднения в построении.)

– Какой мы сделаем вывод, глядя на ваши чертежи?

————–(оценка в баллах)———————-

(Слайд 18) Вывод: Любая точка, лежащая на серединном перпендикуляре равноудалена от концов этого отрезка.

6. (Слайд 19) Индивидуальная и парная работа. (с взаимопроверкой).

Выдаётся каждому ученику карточка (Приложение 4), в которой необходимо сделать отметки на чертеже и заполнить пропуски в тексте.

На слайде – выполненное задание. Контролирует выполнение задания.

—————Баллы в оценочный лист (0-3)————————–

—————Добавляем баллы за активность на уроке (0-3).——————

Ставим оценки: 13-15 баллов – «5», 9-12 баллов -«4».

Итог

(Слайд 20) Домашнее задание.
(Слайд 21) Подводим итог урока.

Ребята, мы с вами сегодня очень дружно и хорошо поработали. Скажите, пожалуйста, что мы с вами узнали нового (ответы учащихся). Что мы с вами делали (строили, формулировали новое свойство, искали решение задачи).

(Слайд 22) Выберите фразеологизм или пословицу, которые характеризуют вашу работу сегодня и запишите:

Шевелить мозгами
Краем уха
Хлопать ушами

(Слайд 23) Урок окончен. Спасибо. Вы все отлично справились.

Пояснительная записка.

Предметная область – математика, 5класс.

Данная тема относится к блоку «Геометрические тела», которая призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Обучает использовать геометрический язык для описания предметов окружающего мира в простейших случаях; способствует формированию универсальных учебных действий: логическому развитию и формированию умения на практике применять знания, полученные на уроке, добывать их и делать выводы.

Тип урока: урок формирования новых знаний. Формы организации учебной деятельности: индивидуальная, фронтальная, развивающая, личностно-деятельностная.

Технологии: использование презентации, работа с бумагой, с чертёжными принадлежностями. Работа с бумагой позволяет развивать практические, прикладные навыки, позволяет усвоить сложные математические понятия легко и просто. Изучение геометрических фигур становится наглядным и доступным даже для слабых учащихся. Кроме того, позволяет развивать коммуникативные и личностные умения и действия учащихся. Осуществляется деятельно-личностный, развивающий подход к обучению. В результате применения мультимедийных средств оптимизируется процесс преподавания предмета.

Соответствует учебнику «Математика. 5 класс» для образовательных учреждений, И.И. Зубарева, А.Г. Мордкович. – М. Мнемозина, 2015.

Приложение 1.

Задания для групповой работы.

Задание 1

1. Разделите отрезок АВ пополам.

Середину назовите точкой D.

2. Через точку D проведите прямую n, перпендикулярную отрезку АВ.

3. Выполните задание 2.

Задание 1

1. Разделите отрезок FС пополам.

Середину назовите точкой К.

2. Через точку К проведите прямую