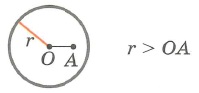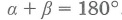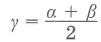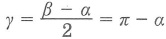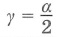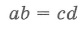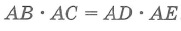Какие свойства точек окружности
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
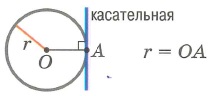
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
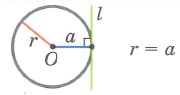
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
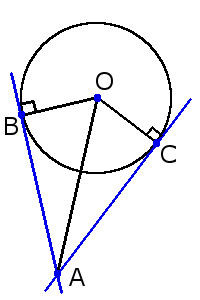
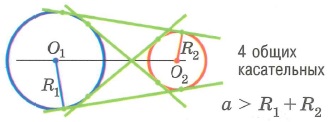
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

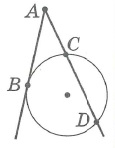
1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
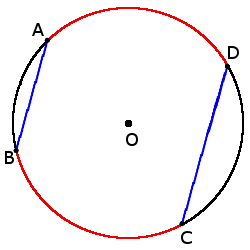
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
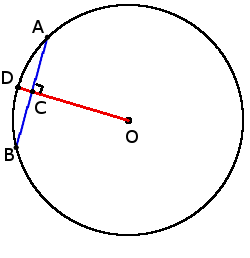
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
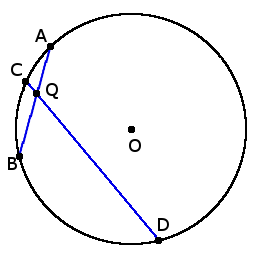
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
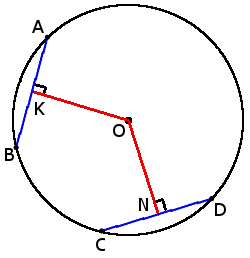
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
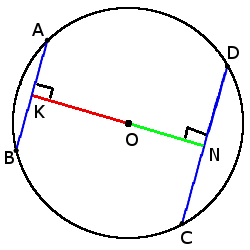
6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
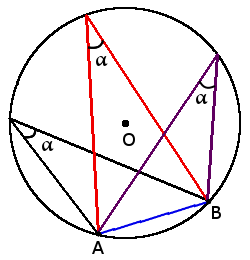
1. Все вписанные углы, которые опираются на одну дугу – равны.
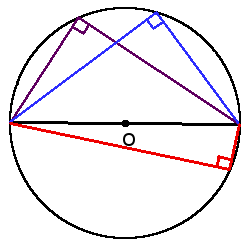
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
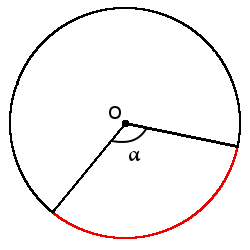
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
Что такое окружность?
Окружность — одна из самых важных кривых линий на плоскости, её можно начертить циркулем или даже натянутой верёвкой, если закрепить один из концов верёвки в данной точке. В любом случае расстояние от всех точек окружности до данной закреплённой точки будет одинаково. Эту точку называют центром окружности, а любой отрезок, который соединяет точку на окружности с её центром, называется радиусом. В переводе с латыни слово радиус означает “спица колеса”. Это не удивительно, ведь можно сказать, что окружность — это математическая модель колеса. Если две любые точки окружности соединить отрезком, то получится хорда. Хорда же в переводе с греческого языка означает “струна”. Если хорда проходит через центр окружности, то её называют диаметром и обычно обозначают буквой . Понятно, что длина диаметра окружности должна быть равна двум её радиусам, то есть . Давайте повторим ещё раз.
Определения.
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки.
Радиус окружности — отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны.
Хорда окружности — отрезок, соединяющий две любые её точки.
Диаметр окружности — это хорда, которая проходит через центр окружности.
Свойство диаметра.
Легко доказать, что диаметр окружности — это самая длинная её хорда. Да, и само слово диаметр в переводе означает “поперечник”. В технике измеряют диаметры колёс, труб, винтов и гвоздей и обозначают их таким значком .
Давайте сформулируем данное свойство диаметра как теорему.
Теорема.
Любая хорда окружности не превышает её диаметра.
Доказательство. Возьмём на окружности с центром в точке и радиусом любые две точки и . Если хорда проходит через центр окружности, то по определению она будет её диаметром и равна . Если же хорда не содержит центра окружности, то образуется треугольник . Тогда для него должно выполняться неравенство треугольника: . Значит, в любом случае хорда не может быть больше диаметра окружности. Что и требовалось доказать.
Полезно знать, что в геометрии диаметр можно определить не только для окружности или круга. Он есть у квадрата, треугольника, да и вообще у многих других геометрических фигур. А знаете, что называют диаметром фигуры? Так же, как и у окружности, диаметр фигуры — это самая длинная её хорда.
Определение.
Диаметр геометрической фигуры — это самое большое расстояние между любыми двумя точками этой фигуры.
Что такое круг?
Чем круг отличается от окружности? Каждый человек интуитивно понимает, что круг — это то, что находится “внутри ” окружности. Можно даже сказать, что для окружности круг — это её внутренняя область. Правда, работать с таким определением не очень удобно.
Как же можно удобно определить круг? Предположим, что один фермер выпустил пастись свою козу на луг, а чтобы она далеко не ушла, привязал её к колышку в точке с помощью верёвки длины . В течение дня коза выщипала траву везде, куда она смогла дотянуться. Как выглядит та часть луга, где паслась коза, и где теперь не стало травы?
Ясно, что коза не сможет отойти от колышка, к которому она привязана, дальше чем на длину своей верёвки. И она сможет дотянуться до любого места, которое ближе находится к этому колышку, чем длина её верёвки. Таким образом, коза выщиплет траву внутри круга с центром в точке и радиусом , равным длине её натянутой верёвки. Теперь мы с вами уже можем дать следующее определение.
Определение.
Круг — это множество всех точек плоскости, удалённых от данной точки не более, чем на длину данного отрезка.
Данная точка называется центром круга, а указанный отрезок — радиусом круга.
Круг с центром в точке и радиусом обозначают так: круг .
Разберём несколько примеров решения задач.
Пример 1. В окружности провели две хорды и , равные радиусу этой окружности. Найдите угол .
Решение. Отметим центр данной нам окружности и проведем радиусы в точки , и . Тогда треугольники и будут равносторонними. Значит, их углы и будут равны . Искомый угол равен их сумме, поэтому он будет равен .
Ответ: .
Пример 2. В окружность радиуса вписан квадрат. Найдите площадь этого квадрата.
Решение. Отметим центр данной нам окружности и проведем из него радиусы во все вершины квадрата .
Поскольку у квадрата все стороны равны, а радиусы окружности равны по определению, треугольники , , и будут равны по трём сторонам. Значит, равны все их углы при вершинах в точке . Сумма этих четырёх углов равна , поэтому каждый угол равен .
Запишем теорему Пифагора для треугольника : . Значит, сторона квадрата равна , а его площадь равна квадрату стороны. То есть, она равна .
Ответ: .
Пример 3. В окружность радиуса вписан равносторонний треугольник. Найдите расстояние от центра окружности до стороны этого треугольника.
Решение. Соединим центр окружности с вершинами равностороннего треугольника , который вписан в эту окружность. Поскольку все стороны треугольника равны, а радиусы окружности равны по определению, то равнобедренные треугольники , и будут равны по трём сторонам. Поэтому будут равны шесть углов при основаниях этих треугольников. Обозначим величину каждого из них через и запишем сумму всех углов треугольника : . Откуда .
Расстояние от точки до прямой линии — это длина перпендикуляра, опущенного из этой точки на данную прямую. Давайте опустим из точки перпендикуляр на сторону нашего треугольника и найдём его длину. Треугольник будет прямоугольным, причём его угол при вершине будет равен . Значит, по известному свойству катет против угла равен половине гипотенузы. То есть, .
Ответ: .
Источник
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. Взаимное расположение окружности и прямой, окружности и точки, двух окружностей. Свойства углов, связанных с окружностью. Метрические соотношения в окружности
Свойства окружностей. Прямые, отрезки и углы, связанные с окружностью. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Прямые, отрезки и углы, связанные с окружностью: | |||
 | Центральный угол измеряется дугой, на которую он опирается. Если отнести длину этой дуги к радиусу окружности то получится радианная мера угла. | ||
Взаимное расположение окружности и прямой: | |||
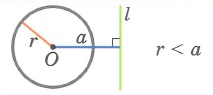
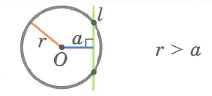
1. Окружность и прямая не имеют общих точек |
2. Окружность и прямая имеют 2 общие точки (l – секущая) |
3. Окружность и прямая имеют 1 общую точку (l – касательная) | |
Взаимное расположение окружности и точки: | |||
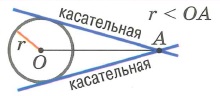
1. Точка лежит вне окружности (2 касательные через точку А) |
2. Точка лежит внутри окружности (нет касательных через точку А) |
3. Точка лежит на окружности (1 касательная через точку А) | |
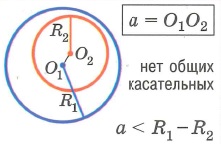
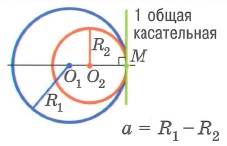
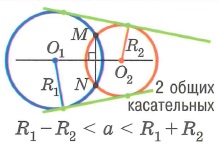
Взаимное расположение двух окружностей: | |||
1. Одна окружность лежит внутри другой. |
2. Одна окружность касается другой изнутри. |
3. Окружности пересекаются. | |
4. Одна окружность касается другой снаружи или одна окружность лежит вне другой. | |||
Свойства углов, связанных с окружностью: | |||
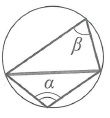
Вписанный угол равен половине центрального, опирающегося на ту же дугу:
|  | Все вписанные углы, опирающиеся на одну и ту же дугу равны: | 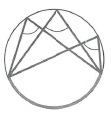 |
| Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны: | 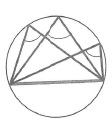 | Любые два вписанных угла, опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°=π
|  |
| Все вписанные углы, опирающиеся на диаметр, прямые: | 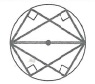 | Угол между пересекающимися хордами:
| 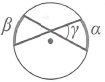 |
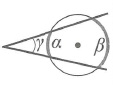
Угол между секущими, пересекающимися вне окружности:
|  | Угол между касательной и секущей: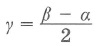 | 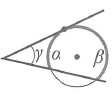 |
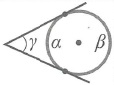
Угол между касательными:
|  | Угол между касательной и хордой:
|  |
Метрические соотношения в окружности (длины отрезков): | |||
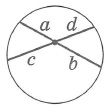
Отрезки пересекающихся хорд связаны соотношением:
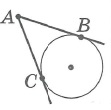
|  | Отрезки касательных, проведенных из общей точки, равны:
|  |
Квадрат длины отрезка касательной равен произведению длин отрезков секущей, проведенной из той же точки:
|  | Произведения длин отрезков секущих, проведенных из общей точки, равны:
|  |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Источник
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности.

Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
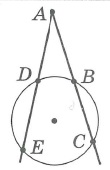
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности (d=2R).
OA – радиус, DE – хорда, BC – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны (AC=BC).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Часть окружности, заключенная между двумя точками, называется дугой окружности.
Например, хорда AB стягивает две дуги: ∪AMB и ∪ALB.
Теорема 4:
Равные хорды стягивают равные дуги.
Если AB=CD, то ∪AB=∪CD
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠AOB – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается. ∪AB=∠AOB=α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360°.
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ACB – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается. ∠ACB=∪AB2=α2∪AB=2⋅∠ACB=α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
∠MAN=∠MBN=∠MCN=∪MN2=α2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90°.
MN – диаметр.
∠MAN=∠MBN=∪MN2=180°2=90°
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α.
Градусная мера дуги ∪AB равна градусной мере дуги ∪CD и равна α.
∪AB=∪CD=α
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
l=2πR
Длина дуги окружности, на которую опирается центральный угол α равна:
lα=πR180∘⋅α
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S=πR2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: Sα=πR2360°⋅α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S=πR2360°⋅α−12R2sinα
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
asin∠A=bsin∠B=csin∠C=2R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Модуль геометрия: задания, связанные с окружностями.
Источник