Какие свойства сложения векторов вы знаете

Предварительные сведения
Перед тем как вводить свойства векторов, введем, непосредственно, понятие вектора, а также понятия их сложения, умножения на число и их равенства.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу – его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ – (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Чтобы ввести определение равенства двух векторов, сначала нужно разобраться с такими понятиями, как коллинеарность, сонаправленность, противоположная направленность двух векторов, а также длину вектора.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Осталось ввести понятие сложения векторов, а также их умножения на число.
Определение 8
Суммой векторов $overline{a+b}$ будем называть вектор $overline{c}=overline{AC}$, который построен следующим образом: От произвольной точки A отложем $overline{AB}=overline{a}$, далее от точки $B$ отложем $overline{BC}=overline{b}$ и соединим точку $A$ c точкой $C$ (рис. 6).
Определение 9
Произведением вектора $overline{a}$ на $k∈R$ будем называть вектор $overline{b}$ который будет удовлетворять условиям:
- $|overline{b}|=|k||overline{a}|$;
- $overline{a}↑↑overline{b}$ при $k≥0$ и, $overline{a}↑↓overline{b}$ при $k
Свойства сложения векторов
Введем свойства сложения для трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$:
Коммутативность сложения векторов:
$overline{α}+overline{β}=overline{β}+overline{α}$
Ассоциативность трех векторов по сложению:
$(overline{α}+overline{β})+overline{γ}=overline{α}+(overline{β}+overline{γ})$
Сложение с нулевым вектором:
$overline{α}+overline{0}=overline{α}$
Сложение противоположных векторов
$overline{α}+(overline{-α})=overline{0}$
Все эти свойства можно легко проверить с помощью построений таких векторов с помощью определения 8. В двух первых сравнением построенных векторов с правой и левой частей равенства, а в третьем и четвертом с помощью построения вектора с левой стороны.
Свойства умножения вектора на число
Введем свойства умножения для двух векторов $overline{α}$, $overline{β}$ и чисел $a$ и $b$.
- $a(overline{α}+overline{β})=aoverline{α}+aoverline{β}$
- $overline{α}(a+b)=overline{α}a+overline{α}b$
- $(ab)overline{α}=a(boverline{α})=b(aoverline{α})$
- $1cdot overline{α}=overline{α}$
Все эти свойства можно легко проверить с использованием определений 8 и 9. В двух первых сравнением построенных векторов с правой и левой частей равенства, в третьем сравнением всех векторов, входящих в равенство, и в четвертом с помощью построения вектора с левой стороны.
Пример задачи
Пример 1
Провести сложение векторов
$2overline{AB}+(2overline{BC}+3overline{AC})$
Решение.
Используя свойство сложения 2, получим:
$2overline{AB}+(2overline{BC}+3overline{AC})=(2overline{AB}+2overline{BC})+3overline{AC}$
Используя свойство умножения на число 1, получим:
$(2overline{AB}+2overline{BC})+3overline{AC}=2(overline{AB}+overline{BC})+3overline{AC}=2overline{BC}+3overline{AC}=5overline{AC}$
Ответ: $5overline{AC}$.
Источник
Отрезок, который имеет направление, называется вектором. По сути, эта линия, характеризующаяся определённой длиной. Так как с математической точки зрения это выражение, то с ним можно выполнять различные операции. Простейшими являются действия вычитания двух и более векторов и их сложение. Выполняются они по правилам геометрии и алгебры.
Общие сведения
Понятие вектор используется как в физике, так и в математике. С его помощью обозначают действие различных сил, указывают их направление, определяют движение. По сути, это величина, противопоставляемая массе, объёму, плотности, температуре, то есть «скалярам». Согласно определению вектор — это отрезок, имеющий строгое направление. Точку, из которой он выходит, называют начальной, а в которой заканчивается — конечной.
Обозначают отрезок помощью заглавных латинских букв, сверху которых ставится чёрточка. Рисуют же его с помощью прямой ограниченной линии.
Например, запись AB обозначает, что точка A является началом, а B концом. В некоторых случаях для кратности отрезки допустимо обозначать одной маленькой буквой, так: AB = a.
Векторная запись используется тогда, когда невозможно величины описать с помощью одного числа. Численное значение выражение определяется длиной отрезка или его модулем. Эта величина является скалярной. В том случае если начало и конец ограниченной линии совпадают, то говорят о нулевой линии. Обозначают её цифрой 0.
Векторы, расположенные на плоскости или в пространстве, по отношению друг к другу могут быть:
- коллинеарными — отрезки лежат на одной линии или ей параллельны;
- соноправленными — замкнутые линии направление которых одинаковое;
- противоположными — вектора направлены в разные стороны;
- ортогональными — перпендикулярными друг другу;
- компланарными — лежащими на одной плоскости или ей параллельные;
- равными — ограниченными прямыми, совпадающими как по направлению, так и по величине.
Так как вектора — это выражения, то с ними можно выполнять различные действия. Их возможно складывать, вычитать, умножать на число. При работе с векторными величинами используют декартовую систему координат. В ней прямую замкнутую линию раскладывают по базису и определяют координаты её точек. Другими словами, выполняют проекции отрезков на оси. Непосредственно за базис берут орты.
Если известны начальные координаты и конечные, то текущие вычисляют путём вычитания из последних первые. Существующая возможность записать любое геометрическое свойство, используя координаты, позволяет отойти от геометрии и использовать для вычислений алгебру.
Сложение координат
Существует простое правило применимое для направленных отрезков и позволяющее найти их сумму. Заключается оно в следующем: если необходимо прибавить один вектор к другому описывающийся каждый своими координатами, достаточно сложить соответствующие их орты. Например, предположим есть два вектора a и b. Первый отрезок имеет координаты (ax; ay), а второй (bx;by). При их сложении получится новый вектор c. В результате действия его координаты будут c (ax + bx; ay + by).
Это теорема доказывается просто. Пусть даны отрезки f (x 1; y 1) и g (x 2; y 2). В системе координат относительно рассматриваемых векторов получится: f = x 1 a + y 1 b; g = x 2 a + y 2 b. Тогда искомая сумма будет: f + g = x1a + y1b + x2a + y2b = a (x 1 + x 2) + b (y 1 + y 2). Что и нужно было доказать. Это правило применимо к векторам имеющим любые координаты. Например, пусть есть a (1; 2), b (-3; 1). Нужно найти их сумму. С помощью формулы сложения получится новый направленный отрезок с координатами a + b = (1 — 3; 2 + 1) = (-2; 3).
Как и при операциях с простыми числами при работе с векторными выражениями используют различные их свойства. Существует три правила сложения векторов:
Приведённые свойства соответственно называют переместительным, сочетательным, нулевым законом. Например, предположим есть два направленных отрезка a (2; 2) и b (-4; 1). Согласно первому свойству, очерёдность значения не имеет, поэтому что при прибавлении b к a, что при a к b результат будет одинаковый: a + b = (2 -4; 2 + 1) = (-2; 3), b + a = (-4 + 2; 1 +2) = (-2; 3). По аналогии можно проверить правильность утверждения и двух оставшихся свойств.
Следует отметить, что при сложении двух противоположных ограниченных прямых сумма будет равняться нуль-вектору: a + (-a) = 0. Это утверждение не требует доказательства, так как здесь используется фундаментальный закон алгебры — правило знаков.
Правило параллелограмма
По сути, все операции с векторными выражениями сводятся к их приращению или уменьшению. Если координаты точек неизвестны, то алгебраический метод складывания не подходит. В таком случае используют геометрические операции. Одним из способов, позволяющих сложить два неколлинеарных вектора, является правило параллелограмма или прямоугольника при перпендикулярном направлении складываемых отрезков.
Сформулировать способ можно следующим образом: если имеются два отрезка не лежащие на параллельной прямой и не принадлежащие ей, то нужно достроить данные вектора до параллелограмма. Для этого необходимо взять произвольную точку и отложить от неё отрезок AB равный первому вектору, и AD совпадающий со вторым. При этом необходимо придерживаться соотношения геометрии наклона. Затем достроить необходимые параллельные прямые таким образом, чтобы образовался параллелограмм ABCD. Если в такой фигуре провести диагональ, то её длина и будет равняться сумме складываемых отрезков.
Доказать правильность утверждения можно следующими доводами. Пусть имеются две ограниченные линии a и b. От точки A можно отложить первый отрезок конец, которого обозначить как B, и второй, с точкой D. Теперь через D и B возможно провести соответственно параллельные прямые AB и AD. Место, в которой они пересекутся, пусть будет обозначено как С. Тогда используя признак параллельности двух пар прямых в фигуре ABCD, можно утверждать, что это параллелограмм. Вектор AC = a + b. Это следует из равенства отрезков AD = BC и теоремы о подобных треугольниках.
Пример задания. Определить, чему равна сумма двух отрезков длиной 2 см и 1 см расположенные друг к другу под углом 45. Для того чтобы воспользоваться правилом, нужно взять листочек в клеточку и построить два вектора, исходящие из одной точки O. Тогда первый отрезок будет OA, а второй OB. Затем достроить прямые таким образом, чтобы на рисунке получился параллелограмм. Новая полученная точка пусть будет D. Теперь с помощью линейки можно измерить диагональ фигуры, длина которой и будет искомой суммой. В ответе должно получиться, что OA + OB = OD = 3 см.
Простыми словами это правило можно рассказать так: сумма двух отрезков будет равняться диагонали параллелограмма, построенного на исходных векторах. Эта теорема чаще используется не в геометрии, а физике, например, при сложении сил.
Альтернативные методы
Операцию по сложению двух векторов можно выполнить и с помощью правила треугольника. Делается это так. Выбирается любая точка на плоскости, от которой откладываются два вектора. При этом необходимо соблюдать их размерность и наклон по отношению друг к другу. Затем две конечные точки соединяют прямой. Её длина и будет искомой величиной. То есть в итоге должна получиться равнобедренная фигура.
Применение метода сложения векторов по правилу треугольника позволяет довольно легко находить сумму для трёх и более отрезков. Для этого сначала вычисляют результат сложения для двух любых линий, а после прибавляют к полученной ограниченной прямой третью и так далее.
При сложении нескольких векторов удобно выполнять следующую последовательность построений:
- от выбранной точки пространства рисуется вектор, равняющийся первому слагаемому;
- от конечной точки откладывается вектор, совпадающий со вторым слагаемым;
- приведённая последовательность потеряется необходимое число раз;
- прямой линией соединяется точка, с которой началось построение с конечной последнего вектора;
- длина полученного отрезка и будет являться результатом сложения.
Этот способ получил название метод многоугольника. Он довольно часто применяется на практике, позволяя, довольно просто выполнить нахождение суммы. Из правила треугольника, а, следовательно, и многоугольника, вытекает следствие, которое подтверждает, что если складывается отрезок с нулевым векторным выражением, то в ответе получится длина, совпадающая со значимым слагаемым.
Следует отметить, что методы используются только, если направление отрезков является сонаправленным.
Если же отрезки неколлинеарные, то от конца одного откладывается другой. Тогда искомая сумма будет равняться длине линии, первой точкой которой будет начало одной векторной прямой, а конец совпадать с точкой, завершающей другую. То есть сумма — это отрезок, начало которого совпадает с началом обеих линий, а длина равна разности их длин, при этом направление его будет совпадать с тем что больше по длине.
Предыдущая
ГеометрияПлощадь треугольника по координатам вершин – формулы для расчета
Следующая
ГеометрияПлощадь прямоугольной трапеции через угол и основания
Источник
- Главная
- Справочник
- Геометрия
- Вектора
- Сложение и вычитание векторов
Векторы: ( vec{a} ), ( vec{b} ), ( vec{c} ), ( vec{u_1} ), ( vec{u_2},;ldots; )
Нулевой вектор: ( vec{0} )
Координаты векторов: ( {X_1} ), ( {Y_1} ), ( {Z_1} ), ( {X_2} ), ( {Y_2} ), ( {Z_2} )
Определение 1 Если точка ( A ) начала какого-либо вектора ( overrightarrow{a} ), то говорят, что вектор ( overrightarrow{a} ) отложен от точки ( A ) (рис. 1).

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow{a} ).
Существование: Имеем два следующих случая:
Вектор ( overrightarrow{a} ) – нулевой.
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow{KK} ).
Вектор ( overrightarrow{a} ) не является нулевым.
Пусть точка ( A ) является началом вектора ( overrightarrow{a} ), а точкой ( B ) – конец вектора ( overrightarrow{a} ). Проведем через точку ( K ) прямую ( b ) параллельную вектору ( overrightarrow{a} ). Будем откладывать на прямой отрезки ( left|KLright|=|AB| ) и ( left|KMright|=|AB| ). Рассмотрим векторы ( overrightarrow{KL} ) и ( overrightarrow{KM} ). Из этих двух векторов нужный нам вектор — вектор, сонаправленный с вектором ( overrightarrow{a} ) (рис.2)

Рисунок 2.
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Суммой двух векторов ( vec{a} ) и ( vec{b} ) называется третий вектор ( vec{c} ), проведенный из начала ( vec{a} ) к концу ( vec{b} ), если начало вектора ( vec{b} ) совпадает с концом вектора ( vec{a} ).
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
( vec{c} = vec{a} + vec{b} )

Суммой нескольких векторов ( vec{a_1} ),( vec{a_2} ), ( vec{a_3},;ldots ) называется вектор ( vec{c} ), получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
( vec{c} = vec{a_1} + vec{a_2} + vec{a_3} + ldots + vec{a_n} )

Коммутативный закон сложения
( vec{a} + vec{b} = vec{b} + vec{a} )
Ассоциативный закон сложения
( left( {vec{a} + vec{b}} right) + vec{c} = vec{a} + left( {vec{b} + vec{c}} right) )
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec{a} + vec{b} = left( {{X_1} + {X_2},{Y_1} + {Y_2},{Z_1} + {Z_2}} right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow{a} ) выполняется равенство
[ overrightarrow{a}+overrightarrow{0}=overrightarrow{a} ]
Для произвольных точек ( A, B и C ) справедливо следующее равенство
[ overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC} ]
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов
Разностью двух векторов ( vec{a} ) и ( vec{b} ) называется вектор ( vec{c} ) при условии:
( vec{c} = vec{a} – vec{b} ), если ( vec{c} + vec{b} = vec{a} )
Разность векторов ( vec{a} ) и ( vec{b} ) равна сумме вектора ( vec{a} ) и противоположного вектора ( -vec{b} ):
( vec{a} – vec{b} = vec{a} + left( -vec{b} right) )

Разность двух одинаковых векторов равна нулевому вектору :
( vec{a} – vec{a} = vec{0} )
Длина нулевого вектора равна нулю:
( left| vec{0} right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec{a} – vec{b} = left( {{X_1} – {X_2},{Y_1} – {Y_2},{Z_1} – {Z_2}} right) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow{a } ) и действительное число ( k ).
Определение Произведением вектора ( overrightarrow{a } ) на действительное число ( k ) называется вектор ( overrightarrow{b } ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow{b } ) равна ( left|overrightarrow{b }right|=left|kright||overrightarrow{a }| );
Векторы ( overrightarrow{a } ) и ( overrightarrow{b } ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow{b }=koverrightarrow{a } ).
Пусть даны векторы ( overrightarrow{a} ) и ( overrightarrow{b} ). Построить вектор ( overrightarrow{a}-overrightarrow{b} ).
Построим произвольную точку ( O ) и отложим от нее векторы ( overrightarrow{OA}=overrightarrow{a} ) и ( overrightarrow{OB}=overrightarrow{b} ). Соединив точку ( B ) с точкой ( A ), получим вектор ( overrightarrow{BA} ).

По правилу треугольника для построения суммы двух векторов видим, что
[ overrightarrow{OB}+overrightarrow{BA}=overrightarrow{OA} ]
То есть
[ overrightarrow{b}+overrightarrow{BA}=overrightarrow{a} ]
Из определения 2, получаем, что
[ overrightarrow{a}-overrightarrow{b}=overrightarrow{BA} ]
( overrightarrow{a}-overrightarrow{b}=overrightarrow{BA} ).
Уровень8 класс ПредметМатематика СложностьПростая
Дан прямоугольный параллелепипед ( ABCDA_1B_1C_1D_1 ). Доказать, что ( overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1}=overrightarrow{AC_1} )
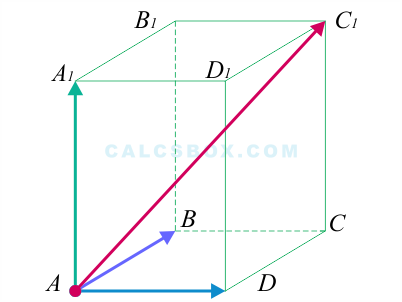
Воспользуемся свойством правила треугольника ( overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC} ), получим:
[ overrightarrow{AC_1}=overrightarrow{AD}+overrightarrow{DC}+overrightarrow{CC_1} ]
Так как ( overrightarrow{DC}=overrightarrow{AB}, overrightarrow{CC_1}=overrightarrow{AA_1} )
То есть
[ overrightarrow{AC_1}=overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1} ]
ч. т. д.
Уровень8 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Вектор – это направленный отрезок, то есть отрезок, имеющий длину и определенное направление.
Координатами вектора называются проекции вектора на оси координат
Декартовы координаты – система координат, состоящая из двух перпендикулярных осей.
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Создать бесплатно пароль любой длины и уровня сложности для ваших приложений, аккаунтов, соц. сетей, паролей к Windows, зашифрованным архивам и т.д.
Морскую милю приравняли к 1862 метрам, сухопутная американская миля равна 1.609344 километра.
Невозможно создать круговой процесс, результатом которого станет исключительно превращение теплоты, которое получено от нагревателя, в работу.
Ведро́ — сосуд для хранения жидких и сыпучих материалов и транспортировки их на небольшие расстояния.
Источник
