Какие свойства сложения применялись

Математика, 2 класс
Урок № 16. Свойства сложения. Применение переместительного и сочетательного свойств сложения
Перечень вопросов, рассматриваемых в теме:
– Что такое сочетательное свойство сложения?
-В каких случаях можно использовать свойства сложения?
Глоссарий по теме:
Переместительное свойство сложения: слагаемые можно переставлять местами, при этом значение суммы не изменится.
Сочетательное свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.44-47
2. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций/ Глаголева Ю.И., Волкова А.Д.-М.: Просвещение, Учлит, 2017, с.18, 19
3. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.- с.28, 29
Теоретический материал для самостоятельного изучения
Сравним выражения и их значения:
6+9 *9+6
45+5*5+45
Сумма чисел шесть и девять равна сумме чисел девять и шесть.
Сумма чисел сорок пять и пять равна сумме чисел пять и сорок пять.
6+9 =9+6
45+5=5+45
Что заметили?
Значения выражений равны, так как от перестановки слагаемых значение суммы не меняется. Вспомним, как в математике называется данное свойство сложения?
Правильно, оно называется переместительным свойством сложения.
Решим задачу.
В школьном спортзале 3 волейбольных мяча, 5 баскетбольных мячей и 4 футбольных мяча. Сколько всего мячей в спортзале?
Первый способ решения.
Сначала узнаем, сколько волейбольных и баскетбольных мячей, затем прибавим число футбольных мячей. Запишем: к сумме чисел три и пять прибавить четыре, получится двенадцать.
(3+5)+4=12 (м.)
Второй способ решения.
Прибавим к числу волейбольных мячей сумму баскетбольных и футбольных мячей. Запишем: к трем прибавить сумму чисел пять и четыре равно двенадцать.
3+(5+4)=12 (м.)
В обоих случаях получили одинаковый результат, значит, выражения равны между собой. Можем записать так: (3+5)+4=3+(5+4)
Теперь ты знаешь еще одно свойство сложения: результат сложения не изменится, если соседние слагаемые заменить их суммой. Это свойство называется сочетательным свойством сложения.
Знание этих двух свойств сложения позволит нам решать примеры на сложение удобным способом.
Решим выражение: 1+7+9+3=?
Мы знаем, что слагаемые можно менять местами и соседние слагаемые заменять их суммой. Воспользуемся свойствами сложения и найдем сумму.
1+7+9+3= (1+9)+(7+3)=10+10=20
В данном случае удобно сложить попарно 1 и 9, 7 и 3. А затем сложить полученные результаты. Получим 20.
Делаем вывод: используя переместительное и сочетательное свойства сложения можно складывать числа в любом порядке, как удобнее.
Тренировочные задания.
1. Вычислите суммы удобным способом
30 + 3 + 7 + 40 = _________ 4 + 10 + 6 + 70=_______________
Правильный ответ:
1. 30 + 3 + 7 + 40 = (3+7)+(30+40)=80 2. 4 + 10 + 6 + 70= (10+70)+(4+6)
2. Совместите название математического свойства с его значением и выражением
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
9+5+1+5 = (9+1) + (5+5)
9+6 = 6 + 9
Правильный ответ:
Результат сложения не изменится, если соседние слагаемые заменить их суммой.
Слагаемые можно переставлять местами, при этом значение суммы не изменится.
9+5+1+5 = (9+1) + (5+5)
9+6 = 6 + 9
Источник

Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

- Найти наименьшее общее кратное для исходных знаменателей дробей.
- Определить дополнительные множители для числителей (наименьшее общее кратное поделить на знаменатели).
- Найти произведение числителей на дополнительные множители.
- Сложить получившиеся дроби с одинаковым знаменателем.
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
- Найти произведение знаменателя и целой части смешанного числа.
- Прибавить к получившемуся числу числитель дробной части.
- Результат измерений записать в качестве числителя, а число, стоящее под знаком дроби, оставить без изменений.
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
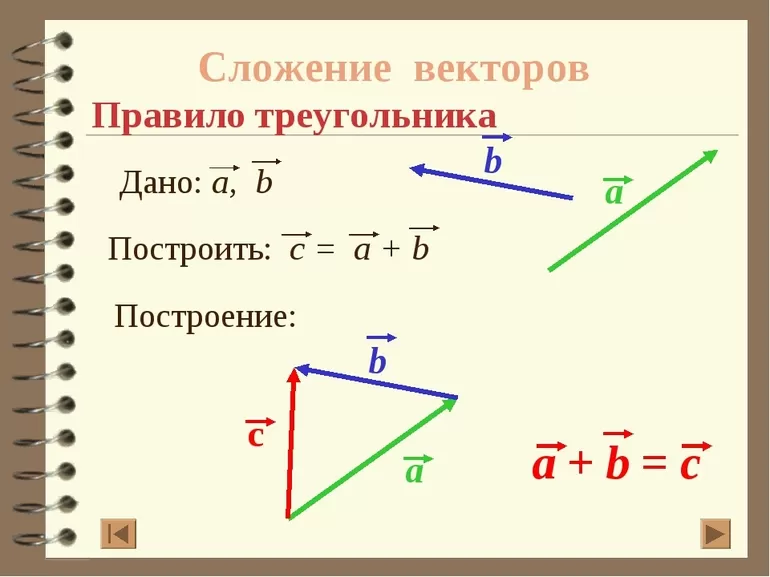
- Метод треугольников: на плоскости необходимо отметить произвольную точку и отложить от нее первый вектор. От конца первого отрезка откладывается второй. Начало первого вектора и конец второго нужно соединить. Полученный отрезок является их суммой. Этот способ используется только для нахождения суммы коллинеарных векторов, не лежащих на параллельных прямых.
- Правило параллелограмма: нужно отметить на плоскости произвольную точку и отложить от нее оба вектора. Фигура достраивается до параллелограмма. Диагональ этого многоугольника является суммой векторов.
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Источник
Сложение натуральных чисел.
Прибавить одно число к другому довольно просто. Рассмотрим пример, 4+3=7. Это выражение означает, что к четырем единицам добавили три единицы и в итоге получили семь единиц. Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.
Числа 3 и 4, которые мы сложили называется слагаемыми. А результат сложение число 7 называется суммой.
Сумма — это сложение чисел. Знак плюс “+”. В буквенном виде этот пример будет выглядеть так:
В буквенном виде этот пример будет выглядеть так:
a+b=c
Компоненты сложения:
a — слагаемое, b — слагаемые, c – сумма.
Если мы к 3 единицам добавим 4 единицы, то в результате сложения получим тот же результат он будет равен 7.
Из этого примера делаем вывод, что как бы мы не меняли местами слагаемые ответ остается неизменным:
4+3=3+4
Называется такое свойство слагаемых переместительным законом сложения.
Переместительный закон сложения.
От перемены мест слагаемых сумма не меняется.
В буквенной записи переместительный закон выглядит так:
a+b=b+a
Если мы рассмотрим три слагаемых, например, возьмем числа 1, 2 и 4. И выполним сложение в таком порядке, сначала прибавим 1+2, а потом выполним сложение к получившейся сумме 4, то получим выражение:
(1+2)+4=7
Можем сделать наоборот, сначала сложить 2+4, а потом к полученной сумме прибавить 1. У нас пример будет выглядеть так:
1+(2+4)=7
Ответ остался прежним. У обоих видов сложения одного и того же примера ответ одинаковый. Делаем вывод:
(1+2)+4=1+(2+4)
Это свойство сложения называется сочетательным законом сложения.
Переместительный и сочетательный закон сложения работает для всех неотрицательных чисел.
Сочетательный закон сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего числа.
(a+b)+c=a+(b+c)
Сочетательный закон работает для любого количества слагаемых. Этот закон мы используем, когда нам нужно сложить числа в удобном нам порядке. Например, сложим три числа 12, 6, 8 и 4. Удобнее будет сначала сложить 12 и 8, а потом прибавить к полученной сумме сумму двух чисел 6 и 4.
(12+8)+(6+4)=30
Свойство сложения с нулем.
При сложении числа с нулем, в результате сумма будет тем же самым числом.
3+0=3
0+3=3
3+0=0+3
В буквенном выражение сложение с нулем будет выглядеть так:
a+0=a
0+a=a
Вопросы по теме сложение натуральных чисел:
Таблица сложения, составьте и посмотрите как работает свойство переместительного закона?
Таблица сложения от 1 до 10 может выглядеть так:
 Второй вариант таблицы сложения.
Второй вариант таблицы сложения.
 Если посмотрим на таблицы сложения, видно как работает переместительный закон.
Если посмотрим на таблицы сложения, видно как работает переместительный закон.
В выражении a+b=c суммой, что будет являться?
Ответ: сумма — это результат сложения слагаемых. a+b и с.
В выражении a+b=c слагаемыми, что будет являться?
Ответ: a и b. Слагаемые – это числа, которые мы складываем.
Что произойдет с числом если к нему прибавить 0?
Ответ: ничего, число не поменяется. При сложении с нулем, число остается прежнем, потому что нуль это отсутствие единиц.
Сколько слагаемых должно быть в примере, чтобы было можно применить сочетательный закон сложения?
Ответ: от трех слагаемых и больше.
Запишите переместительный закон в буквенном выражении?
Ответ: a+b=b+a
Примеры на задачи.
Пример №1:
Запишите ответ у представленных выражений: а) 15+7 б) 7+15
Ответ: а) 22 б) 22
Пример №2:
Примените сочетательный закон к слагаемым: 1+3+5+2+9
1+3+5+2+9=(1+9)+(5+2)+3=10+7+3=10+(7+3)=10+10=20
Ответ: 20.
Пример №3:
Решите выражение:
а) 5921+0 б) 0+5921
Решение:
а) 5921+0 =5921
б) 0+5921=5921
Источник
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Как в равенстве а + b = с называют число а? Число b? Число с? Выражение а + b?
- a — слагаемое
- b — слагаемое
- c — сумма
- a+b — сумма
2. Сформулируйте переместительное свойство сложения.
От перестановки слагаемых сумма не меняется.
3. Как записывают в буквенном виде переместительное свойство сложения?
а + b = b + а
4. Сформулируйте сочетательное свойство сложения.
Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего.
5. Как записывают в буквенном виде сочетательное свойство сложения?
(a + b) + c = a + (b + c)
6. Каким свойством обладает число 0 при сложении?
Если одно из двух слагаемых равно 0, то сумма равна другому слагаемому.
Решаем устно
1. Вычислите:
- 23 + 17 = 40
- 230 + 17 = 247
- 23 + 170 = 193
- 30 — 13 = 17
- 300 — 130 = 170
- 300 — 13 = 287
- 12 • 4 = 48
- 12 • 40 = 480
- 120 • 40 = 4800
- 72 : 8 = 9
- 720 : 8 = 90
- 720 : 80 = 9
2. Назовите два последовательных натуральных числа, сумма которых равна 91.
Любые два последовательных натуральных числа различаются между собой на 1.
1) 90 — 1 = 90 — сумма искомых натуральных чисел без различающих их 1.
2) 90 : 2 = 45 — наименьшее из искомых натуральных чисел.
3) 45 + 1 = 46 — наибольшее из искомых натуральных чисел.
Ответ: 45 и 46.
3. Назовите двузначное число, сумма цифр которого равна наибольшему однозначному числу. Сколько существует таких чисел?
Наибольшее двузначное число — 9.
Значит условию удовлетворяют следующие двузначные числа: 18, 81, 27, 72, 36, 63, 45, 54, 90. Значит существует 9 таких чисел.
Упражнения
167. Найдите сумму:

168. Выполните сложение:

169. Аня и Коля решали задачи. Коля решил 26 задач, а Аня — на 16 задач больше. Сколько задач решили Коля и Аня вместе?

1) 26 + 16 = 42 (задачи) — решила Аня.
2) 42 + 26 = 68 (задач) — решили Коля и Аня вместе.
Ответ: 68 задач.
170. Миша купил книгу за 170 р., что на 12 р. меньше, чем заплатил Петя за свою новую книгу. Сколько рублей заплатили за книги Миша и Петя вместе?

1) 170 + 12 = 182 (рубля) — заплатил за книгу Петя.
2) 170 + 182 = 352 (рубля) — заплатили за свои книги Петя и Миша вместе.
Ответ: 352 рубля.
171. Выполните сложение, выбирая удобный порядок вычислений:
- (42 + 37) + 58 = (42 + 58) + 37 = 100 + 37 = 137
- 29 + (98 + 71) = (29 + 71) + 98 = 100 + 98 = 198
- (215 + 818) + 785 = (215 + 785) + 818 = 1 000 + 818 = 1 818
- 634 + (458 + 166) = (634 + 166) + 458 = 800 + 458 = 1 258
- 183 + 732 + 268 + 317 = (183 + 317) + (732 + 268) = 500 + 1 000 = 1 500
- 339 + 584 + 416 + 661 = (339 + 661) + (584 + 416) = 1 000 + 1 000 = 2 000
- (15 083 + 1 458) + (4 917 + 6 542) = (15 083 + 4 917) + (1 458 + 6 542) = 20 000+ 8 000 = 28 000
- (1 654 + 18 135) + (7 346 + 11 865) = (1 654 + 7 346) + (18 135 + 11 865) = 9 000 + 30 000 = 39 000
172. Используйте свойства сложения при вычислении суммы:
- (146 + 322) + 178 (322 + 178) + 146 = 500 + 146 = 646
- 784 + (179 + 116) = (784 + 116) + 179 = 900 + 179 = 1 079
- 625 + 481 + 75 + 219 = (625 + 75) + (481 + 219) = 700 + 700 = 1 400
- 427 + 88 + 273 + 112 = (427 + 273) + (88 + 112) = 700 + 200 = 900
173. Стена Московского Кремля состоит из трёх участков: южного, восточного и западного. Длина южного участка составляет 685 м, что на 45 м меньше длины восточного. Длина западного участка на 135 м больше длины южного. Сколько метров составляет общая длина стен Московского Кремля?

1) 685 + 45 = 730 (метров) — длина восточной стены Кремля.
2) 685 + 135 = 820 (метров) — длина Западной стены Кремля.
3) 685 + 730 + 820 = 2 235 (метров) — общая длина стен Кремля.
Ответ: 2 235 метров.
174. У Иры в коллекции есть 26 марок, посвящённых историческим событиям, а также марки, посвящённые архитектуре и спорту. Марок по архитектуре у неё на 15 больше, чем по истории, и на 14 меньше, чем на спортивную тему. Сколько марок в коллекции у Иры?

1) 26 + 15 = 41 (марки) — по архитектуре.
2) 41 + 14 = 55 (марок) — посвящённых спорту.
3) 26 + 41 + 55 = 122 (марки) — всего в коллекции Иры.
Ответ: 122 марки.
175. На одной полке было 17 книг, на второй — на 18 книг больше, чем на первой, а на третьей — на 6 книг больше, чем на первой и второй вместе. Сколько всего книг было на трёх полках?

1) 17 + 18 = 35 (книг) — на второй полке.
2) 35 + 17 = 52 (книги) — на первой и второй полке вместе.
3) 52 + 6 = 58 (книг) — на третьей полке.
4) 52 + 58 = 110 (книг) всего на трёх полках.
Ответ: 110 книг.
176. Отправившись в велосипедный поход, группа туристов в первый день проехала 42 км, что на 12 км меньше, чем во второй, а в третий — на 4 км больше, чем в первый и второй вместе. Сколько километров проехали туристы за три дня?

1) 42 + 12 = 54 (км) — туристы проехали во второй день.
2) 42 + 54 = 96 (км) — туристы проехали всего за первый и второй день.
3) 96 + 4 = 100 (км) — туристы проехали в третий день.
4) 96 + 100 = 196 (км) — туристы проехали за три дня всего.
Ответ: 196 км.
177. Упростите выражение:
- (74 + x) + 38 = (74 + 38) + x = 112 + x
- 238 + (а + 416) = (238 + 416) + a = 654 + a
- у + 324 + 546 = y + (325 + 546) = y + 870
- 2 753 + m + 4 199 = (2 753 + 4 199) + m = 6 952 + m
- (b + 457) + (143 + 872) = b + (457 + 143) + 872 = b + 600 + 872 = b + 1 472
- (2 235 + с) + (4 671 + 1 765) = (2 235 + 1 765) + c + 4 671 = (4 000 + 4 671) + c = 8 671 + c
- (1 696 + 3 593) + (р + 1 304) = (1 696 + 1 304) + 3 593 + p = (3 000 + 3 593) + p = 6 593 + p
- (5 432 + 8 951) + (4 568 + а + 1 049) = (5 432 + 4 568) + (8 951 + 1 049) + a = (10 000 + 10 000) + a = 20 000 + a
178. Упростите выражение:
- (56 + а) + 14 = (56 + 14) + a = 70 + a
- 342 + (b + 58) = (342 + 58) + b = 400 + b
- 805 + х + 195 = (805 + 195) + x = 1 000 + x
- m + 4 563 + 1 837 = m + (4 563 + 1 837) = m + 6 400
179. Дядя Фёдор выехал из города в Простоквашино в 15 ч 40 мин и потратил на дорогу 3 ч 50 мин. В котором часу дядя Фёдор приехал в Простоквашино?
1) 15 ч 40 мин + 3 ч 50 мин = (15 ч + 3 ч) + (40 мин + 50 мин) = 18 ч + 90 мин = 18 ч + (60 мин + 30 мин) = (18 ч + 1 ч) + 30 мин = 19 ч 30 мин
Ответ: дядя Фёдор приехал в Простоквашино в 19 часов 30 минут.
180. Поезд отправляется от станции А в 9 ч 57 мин и прибывает на станцию В через 2 ч 36 мин. В котором часу поезд прибывает на станцию В?
1) 9 ч 57 мин + 2 ч 36 мин = (9 ч + 2 ч) + ( 57 мин + 36 мин) = 11 ч + 93 мин = 11 ч + (60 мин + 33 мин) = (11 ч + 1 ч) + 33 мин = 12 ч 33 мин
Ответ: поезд прибывает на станцию В в 12 часов 33 минуты.
181. Найди:
- Как изменится сумма, если одно из слагаемых увеличить на 12? Сумма увеличится на 12.
- Как изменится сумма, если одно из слагаемых увеличить на 23, а второе — на 17? Сумма увеличится на 40 (23 + 17 = 40).
- Как изменится сумма, если одно из слагаемых уменьшить на 34? Сумма уменьшится на 34.
- Как изменится сумма, если одно из слагаемых уменьшить на 16, а второе — на 9? Сумма уменьшится на 25 (16 + 9 = 25).
- Как изменится сумма, если одно из слагаемых увеличить на 28, а второе уменьшить на 15? Сумма увеличится на 13 (28 — 15 = 13).
- Одно из слагаемых увеличили на 3. На сколько надо увеличить второе слагаемое, чтобы сумма увеличилась на 14? Второе слагаемое надо увеличить на 11 (14 — 3 = 11).
- Одно из слагаемых увеличили на 8. Как надо изменить второе слагаемое, чтобы сумма:
- а) увеличилась на 3 — Надо второе слагаемое уменьшить на 5 (8 — 5 = 3).
- б) уменьшилась на 5 — Надо второе слагаемое уменьшить на 13 (13 — 8 = 5).
182. Найдите сумму:
- 76 м 39 см + 41 м 58 см = (76 м + 41 м) + (39 см + 58 см) = 117 м + 97 см = 117 м 97 см
- 4 км 238 м + 3 км 474 м = (4 км + 3 км) + (238 м + 474 м) = 7 км + 712 м = 7 км 712 м
- 64 м 86 см + 27 м 45 см = (64 м + 27 м) + (86 см + 45 см) = 91 м + 131 см = 91 м + (100 см + 31 см) = (91 м + 1 м) + 31 см = 92 м 31 см
- 16 км 527 м + 37 км 783 м = (16 км + 37 км) + (6 527 м + 783 м) = 53 км + 1 310 м = 53 км + (1 000 м + 310 м) = (53 км + 1 км) + 310 м = 54 км 310 м
- 12 ч 24 мин + 9 ч 18 мин = (12 ч + 9 ч) + (24 мин + 18 мин) = 21 ч + 42 мин = 21 ч 42 мин
- 35 мин 17 с + 16 мин 35 с = (35 мин + 16 мин) + (17 с + 35 с) = 51 мин + 52 с = 51 мин 52 с
- 18 ч 42 мин + 14 ч 29 мин = (18 ч + 14 ч) + (42 мин + 29 мин) = 32 ч + 71 мин = 32 ч + (60 мин + 11 мин) = (32 ч + 1 ч) + 11 мин = 33 ч 11 мин
- 53 мин 32 с + 44 мин 56 с = (53 мин + 44 мин) + (32 с + 56 с) = 97 мин + 88 с = (60 мин + 37 мин) + (60 с + 28 с) = 1 ч + (37 мин + 1 мин) + 28 с = 1 ч 38 мин 28 с
183. Найдите сумму:
- 4 дм 6 см + 5 дм 8 см = (4 дм + 5 дм) + (6 см + 8 см) = 9 дм + 14 см = 9 дм + (10 см + 4 см) = (9 дм + 1 дм) + 4 см = 10 дм 4 см
- 8 м 5 см + 6 м 96 см = (8 м + 6 м) + (5 см + 96 см) = 14 м + 101 см = 14 м + (100 см + 1 см) = (14 м + 1 м) + 1 см = 15 м 1 см
- 12 км 29 м + 24 км 92 м = (12 км + 24 км) + (29 м + 92 м) = 36 км 121 м
- 2 т 4 ц 56 кг + 9 т 6 ц 48 кг = (2 т + 9 т) + (4 ц + 6 ц) + (56 кг + 48 кг) = 11 т + 10 ц +104 кг = (11 т + 1 т) + (100 кг + 4 кг) = 12 т + 1 ц + 4 кг = 12 т 1 ц 4 кг
- 3 ч 48 мин + 2 ч 26 мин = (3 ч + 2 ч) + (48 мин + 26 мин) = 5 ч + 74 мин = 5 ч + (60 мин + 14 мин) = (5 ч + 1 ч) + 14 мин = 6 ч 14 мин
- 25 мин 17 с + 7 мин 54 с = (25 мин + 7 мин) + (17 с + 54 с) =32 мин + 71 с = 32 мин + (60 с + 11 с) = (32 мин + 1 мин) + 11 с = 33 мин + 11 с
184. Вместо звёздочек поставьте цифры так, чтобы сложение было выполнено верно:

185. Вместо звёздочек поставьте цифры так, чтобы сложение было выполнено верно:

186. Не выполняя вычислений, расположите данные суммы в порядке возрастания:
- 129 + 288
- 288 + 659
- 782 + 659
- 782 + 943
- 943 + 1 105
- 1 105 + 2 563
187. Найдите сумму наиболее удобным способом:
1) 1 + 2 + 3 + … + 9 + 10
1 + 2 + 3 + … + 9 + 10 = (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5 + 10 = 10 + 10 + 10 + 10 + 5 + 10 = 10 • 4 + 5 + 10 = 40 + 5 + 10 = 55
Комментарий: В данном примере надо сложить 11 чисел. из них:
- есть один десяток
- четыре пары образуют десяток
- число 5
В результате получаем 5 десятков плюс 5, то есть число 55.
2) 1 + 2 + 3 + … + 99 + 100
1 + 2 + 3 + … + 99 + 100 = (1 + 99) + (2 + 98) + (3 + 97) + … + (49 + 51) + 50 + 100 = 100 • 49 + 50 + 100 = 4900 + 50 + 100 = 5 500.
188. Найди:
1) На сколько сумма 1 + 3 + 5 + … + 99 меньше, чем сумма 2 + 4 + 6 + … + 100?
1) 1 + 3 + 5 + … + 99 = (1 + 99) + (3 + 97) + (5 + 95) + … + (49 + 51) = 100 • 25 = 2 500 — слагаемыми являются только нечётные числа, а от 1 до 49 их 25 штук.
2) 2 + 4 + 6 + … + 100 = (2 + 98) + (4 + 96) + (6 + 94) + … + (48 + 52) + 50 + 100 = 100 • 24 + 50 + 100 = 2 400 + 50 + 100 = 2 550 — слагаемыми являются только нечётные числа, а их 24 пары по 100 плюс число 50 плюс число 100.
3) 2 550 — 2 500 = 50
Ответ: на 50.
2) Какая из сумм 1 + 3 + 5 + … + 2 001 и 2 + 4 + 6 + … + 2 000 больше и на сколько?
1) 1 + 3 + 5 + … + 2 001 = (1 + 1 999) + (3 + 1997) + (5 + 1995) + … + (999 + 1 001) + 2 001 = 2 000 • 500 + 2 001 = 1 000 000 + 2 001 = 1 002 001
2) 2 + 4+ 6 + … + 2 000 = (2 + 1998) + (4 + 1996) + (6 + 1994) + … + (998 + 1 002) + 1 000 + 2 000 = 2 000 • 490 + 1 000 + 2 000 = 2 000 + 500 + 1 000 = 1 000 000 + 1 000 = 1 001 000
3) 1 002 001 — 1 001 000 = 1 001
Ответ: сумма 1 + 3 + 5 + … + 2 001 больше суммы 2 + 4 + 6 + … + 2 000 на 1 001.
189. В записи 4 4 4 4 4 4 4 4 поставьте между некоторыми цифрами знак «+» так, чтобы получилось выражение, значение которого равно 500.
444 + 44 + 4 + 4 + 4 = (444 + 44) + (4 + 4 + 4) = 488 + 12 = 500
Ответ: 444 + 44 + 4 + 4 + 4
190. Замените звёздочки числами так, чтобы сумма любых трёх соседних чисел была равна 20: 7, *, *, *, *, *, *, 9.
7, 9 , 4, 7, 9, 4, 7, 9
7 + 9 + 5 = 20; 9 + 4 + 7 = 20; 4 + 7 + 9 = 20 и т.д.
Ответ: 7, 9 , 4, 7, 9, 4, 7, 9.
191. Слава разрезал проволоку на кусочки и составил фигуру, изображённую на рисунке 65. Мог ли Слава разрезать эту же проволоку так, чтобы составить фигуру, изображённую на рисунке 66?
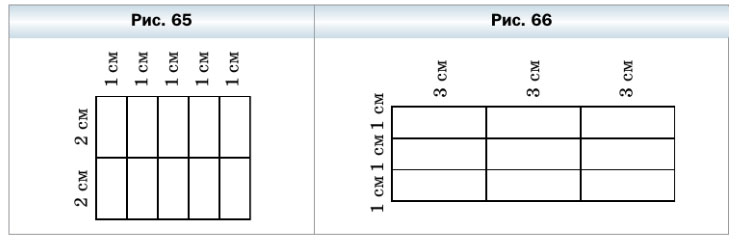
Посчитаем, сколько проволоки Слава потратил на составление первой фигуры:
- 15 кусочков по 1 см
- 12 кусочков по 2 см
1) 15 • 1 + 12 • 2 = 15 + 24 = 39 (см) — проволоки использовано на первую фигуру.
Посчитаем, сколько проволоки Славе потребуется для составления второй фигуры:
- 12 кусочков по 3 см
- 12 кусочков по 1 см
2) 12 • 3 + 12 • 1 = 36 + 12 = 48 (см) — проволоки потребуется для второй фигуры.
3) 39 < 48, значит проволоки с первой фигуры не хватит для изготовления второй фигуры.
Ответ: нет, длины проволоки, использованной для первой фигуры, не хватит для изготовления второй фигуры.
Упражнения для повторения
192. Отметьте на координатном луче натуральные числа, которые больше 6, но меньше 12.

193. Запишите все шестизначные числа, которые больше 999 888 и оканчиваются цифрой 5.
- 999 895
- 999 905
- 999 915
- 999 925
- 999 935
- 999 945
- 999 955
- 999 965
- 999 975
- 999 985
- 999 995
194. Скороход прошёл 24 км за 4 ч. На обратном пути он увеличил скорость на 2 км/ч. Сколько времени он потратил на обратный путь?

1) 24 : 4 = 6 (км/ч) — скорость движения скорохода по пути туда.
2) 6 + 2 = 8 (км/ч) — скорость движения скорохода по пути обратно.
3) 24 : 8 = 3 (часа) — скороход потратил на обратный путь.
Ответ: 3 часа.
195. Вася старше своей сестры Светы на 5 лет. На сколько лет он будет старше Светы через 7 лет?
И через 7 лет, и через 10, и через любое количество лет разница в возрасте между Васей и Светой останется одинаковой — 5 лет. Это происходит потому, что с количество лет прибавляется с каждым годом для всех с одинаковой скоростью.
Ответ: Вася будет старше своей сестры Светы на 5 лет.
Задача от мудрой совы
196. Можно ли таблицу из пяти строк и шести столбцов заполнить натуральными числами так, чтобы сумма чисел каждой строки была равна 30, а сумма чисел каждого столбца — 20?

