Какие свойства сложения и вычитания применены в этом примере
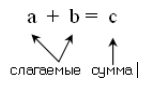
Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
Источник
Сложение натуральных чисел
Для получения числа, которое следует за натуральным, нужно прибавить к нему единицу.
Пример 1
$5 + 1 = 6;$
$48 + 1 = 49$
Для сложения чисел $9$ и $3$ нужно к числу $9$ прибавить $3$ раза единицу.
Получим:
$9 + 3 = 9 + 1 + 1 + 1 = 10 + 1 +1 = 11 + 1 = 12.$
Записывают короче:
$9 + 3 = 12.$
Числа, которые складывают, называют слагаемыми, а результат их сложения — суммой.
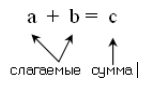
Рисунок 1.
В примере $9 + 3 = 12$:
$9$ и $3$ — слагаемые, $6$ — сумма.
Свойства сложения
Переместительное свойство (коммутативность):
При перестановке слагаемых сумма не меняется
$1 + 5 = 5 + 1 = 6.$
В общем виде переместительное свойство записывается так:
$a + b = b + a$.
Сочетательное свойство (ассоциативность):
Сумма трех и более слагаемых не изменится, если изменить порядок их сложения
$2 + ( 8 + 3 ) = ( 2 + 8 ) + 3 = 13.$
В общем виде сочетательное свойство записывается так:
$a + ( b + c ) = ( a + b ) + c.$
Свойство прибавления нуля:
Если к числу прибавить нуль, то сумма будет равна самому числу
$7 + 0 = 7.$
К этому свойству можно применить переместительное свойство, получим:
Если к нулю прибавить число, то сумма будет равна прибавляемому числу
$0 + 7 = 7.$
В общем виде:
$a + 0 = 0 + a = a.$
Если точкой $C$ разделить отрезок $AB$, то сумма длин отрезков $AC$ и $CB$ будет равна длине отрезка $AB$.

Рисунок 2.
Записывается: $AB = AC + CB$.
Сложение чисел можно удобно выполнять «в столбик»:

Рисунок 3.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Вычитание натуральных чисел
Вычитание — операция, обратная сложению.
Пример 2
На тарелке лежало $7$ яблок, съели $3$ яблока. Сколько яблок осталось на тарелке?
Очевидно, что если к оставшемуся числу яблок $(x)$ добавить $3$ яблока, то их станет $7$:
$x + 3 = 7.$
Таким образом, известно одно слагаемое и сумма, нужно найти второе слагаемое.
Для этого используется вычитание:
$x = 7 – 3 = 4$, т.к. $3 + 4 = 7.$
Число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, — вычитаемым. Результат вычитания называется разностью.
Из данной задачи получаем:
$7$ — уменьшаемое, $3$ — вычитаемое, $8$ — разность.
В общем виде
Если $b + c = a$, то
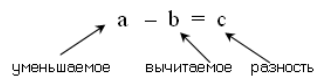
Рисунок 4.
При вычитании натуральных чисел уменьшаемое обязательно должно быть больше вычитаемого:
$11 – 3 = 8; 8 > 3.$
Разность двух чисел находят, чтобы узнать на сколько уменьшаемое больше вычитаемого или на сколько вычитаемое меньше уменьшаемого:
$11$ больше $3$ на $8$.
Свойства вычитания
Свойство вычитания суммы из числа:
$a – ( b + c ) = a – b – c.$
Например, нужно найти значение выражения:
$123 – ( 23 + 45 ) = 123 – 68 = 55.$
Однако намного удобнее считать так:
$123 – ( 23 + 45 ) = 123 – 23 – 45 = 100 – 45 = 55.$
В этом выражении нужно вычесть сумму из числа, а можно сначала вычесть из уменьшаемого одно слагаемое, а потом из полученной разности вычесть второе слагаемое.
Например, найдем результат выражения:
$217 – 33 – 27 = 184 – 27 = 157.$
Но гораздо легче найти сумму вычитаемых и вычесть ее из уменьшаемого:
$217 – 33 – 23 = 217 – ( 33 + 27 ) = 217 – 60 = 157.$
Свойство вычитания числа из суммы:
если $c
если $c
Рассмотрим три примера с одинаковыми результатами.
$( 6 + 5 ) – 4=11 – 4=7;$
$6 + ( 5 – 4 )=6 + 1=7;$
$( 6 – 4 ) + 5=2 + 5=7.$
Откуда получаем: $( 6 + 5 ) – 4=6 + ( 5 – 4 )=( 6 – 4 ) + 5.$
Если нужно вычесть число из суммы, можно вычесть его из любого слагаемого и к полученной разности прибавить другое слагаемое.
Вычитаемое обязательно должно быть меньше слагаемого, из которого его вычитают, или равным ему.
Пример 3
$( 234 + 123 ) – 134=357 – 134=223.$
Но намного удобнее считать так:
$( 234 + 123 ) – 134=234 – 134+ 123=100+ 123=223.$
Если из числа вычесть нуль, оно не изменится:
$a – 0 = a.$
Если из числа вычесть это же число, получим нуль:
$a – a = 0.$
Т.к. $9 + 0 = 9$, то по смыслу вычитания имеем:
$9 – 9 = 0$ или $9 – 0 = 9.$
Результат вычитания удобно находить «в столбик»:
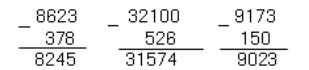
Рисунок 5.
Если точкой $C$ разделяется отрезок $AB$, то разность длин отрезков $AB$ и CB$ равна длине отрезка $AC.$

Рисунок 6.
Записывается: $AB – CB = AC$ или $AB – AC = CB.$
Если $AB = 7$ см, а $CB = 4$ см, то $AC = 7 – 4 = 3$ см.
Пример 4
Решить уравнение $63 – x = 55.$
Решение:
$x = 63 – 55$, откуда $x = 8.$
Число $8$ называется корнем уравнения $63 – x = 55$, т.к. получаем верное равенство $63 – 8 = 55.$
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Источник
КСП по математике в 1 классе
2 четверть 8 урок
*В контексте тем:
«Моя семья и друзья», «Мир вокруг нас»
Школа:
Дата: «____»____________20___г.
ФИО учителя:
Класс: 1 «____» класс.
Количество присутствующих:
отсутствующих:
Тема урока:
Связь сложения и вычитания
Цели обучения, которые достигаются на данном уроке (ссылка на учебную программу):
1.1.2.4 составлять, знать и применять таблицу сложения однозначных чисел без перехода через десяток
1.1.2.3 применять переместительное свойство сложения;
1.2.1.1 составлять, читать, записывать и распознавать числовые выражения (суммы, разности)
1.5.2.2 использовать знаки «+», «-», «=»
Цели урока:
применять переместительное свойство сложения; свойство 0 и 1;
составлять, знать и применять таблицу сложения однозначных чисел без перехода через десяток;
использовать знаки «+», «-», «=».
Критерии успеха
Установить зависимость между действиями сложения и вычитания на основе взаимосвязи компонентов.
Этот урок является обобщающим по теме взаимосвязи между результатами действий сложения и вычитания и изменением компонентов. Урок подготавливает первоклассников к введению понятия «переместительное свойство сложения». В ходе урока ребята в игровой форме научатся составлять примеры на сложение и вычитание, установят, что эти действия являются взаимосвязанными. Вот, допустим, к примеру 8 + 2 = 10 можно составить обратные:
10-2 = 8.
10-8 = 2.
Привитие
ценностей
Ценности, основанные на национальной идее «Мәңгілік ел»: казахстанский патриотизм и гражданская ответственность; уважение; сотрудничество; труд и творчество; открытость; образование в течение всей жизни.
Межпредметные
связи
Навыки
использования
ИКТ
На данном уроке учащиеся используют
Предварительные
знания
Ход урока
Этапы урока
Запланированная деятельность на уроке
Ресурсы
Начало урока
Решение задач (устно)
На столе стояло 6 тарелок. Мама поставила еще 4. сколько тарелок стало?
Мальчик в сентябре прочитал 2 книги, а в октябре 3 книги. В ноябре он прочитал столько книг, сколько за сентябрь и октябрь вместе. Сколько книг прочитал мальчик за ноябрь?
На новогодней елке висело 5 шариков, 4 шишки, а зайчиков столько, сколько шариков и шишек вместе. Сколько было на елке зайчиков?
В школьном парке росло 4 клена и 2 карагача, а тополей столько, сколько кленов и карагачей вместе. Сколько росло кленов?
У Саши было 7 открыток. 3 открытки он подарил. Сколько открыток у него осталось?
В магазине было 5 ящиков яблок. 2 ящика продали. Сколько ящиков осталось?
Вводное задание. Предложите детям поиграть в настольные игры. Разделите класс на группы по четыре человека. Используйте для начала урока
«волшебный» мешочек с числами. Каждая группа вытягивает карточки, на которых написаны три однозначных числа, с помощью которых можно составить примеры.
Спросите:
Какие примеры можно составить, используя эти числа? (примеры на сложение и вычитание)
Как взаимосвязаны сложение и вычитание? Выслушайте предположения школьников. Сообщите, что целью урока является поиск ответа на эти вопросы.
Ход игры: по сигналу учителя каждый человек в группе составляет и записывает один пример. Дальше передвигает карточку следующему игроку. Игра считается законченной, если на карточке записано четыре примера. Первоклассники, закончившие работу в группе, должны взяться за руки и поднять их вверх, сообщив таким образом преподавателю о завершении работы. Составленные примеры прикрепляются к доске для обсуждения.
Например, если ребята вытянули числа 7,2,9, то они могут составить примеры:
7+ 2 = 9;
2+ 7 = 9;
9-7 = 2;
9-2 = 7.
Побеждает группа, которая быстрее справилась с заданием.
Важно обращать внимание учащихся на ведение диалога в группах:
каждый человек в группе должен иметь право голоса;
важно мнение каждого;
при обсуждении нельзя повышать голос и громко спорить;
необходимо уметь договариваться.
Вывод: действия сложения и вычитания взаимосвязаны. К примеру на сложение можно составить обратный пример на вычитание.
Повторите названия компонентов сложения (слагаемое, слагаемое, значение суммы) и вычитания (уменьшаемое, вычитаемое, значения разности).
Критерии успеха
Середина урока
Рассмотри примеры, составленные по таблице сложения. Работа проводится фронтально. Задание направлено на закрепление полученного вывода. Ребята еще раз анализируют таблицу сложения под руководством учителя, определяют, как по таблице составить примеры на сложение и обратные примеры на вычитание. При выполнении данного задания следует обратить особое внимание на развитие навыков моделирования. Схематичное изображение компонентов действий направлено на то, чтобы наглядно продемонстрировать, как взаимосвязаны действия сложения и вычитания. Эти знания в дальнейшем будут использоваться при решении уравнений и задач.
Реши пример: 4 + 3 = ? Задание закрепляет правило: к примеру на сложение можно составить два обратных примера на вычитание. Учащиеся в парах смогут составить примеры, опираясь на образец, приведенный в учебнике. К примеру 8 + 2 = 10 можно составить обратные примеры:
10-2 = 8.
10-8 = 2.
Гусеницы. Дети будут составлять взаимообратные примеры. При выполнении задания учащиеся смогут пользоваться таблицей сложения и применять знания о взаимосвязи действий сложения и вычитания.
Ответы
4,4;
2, 7;
10, 6, 4.
Попробуй. Задание направлено на развитие наблюдательности при составлении и решении четырех взаимосвязанных примеров.
Учебник:
Связь сложения и вычитания, с. 82—83.
Рабочая тетрадь:
Рабочий лист 79 «Связь сложения и вычитания», с. 81.
Рабочий лист 80 «Взаимообратные действия», с. 82.
Ресурсы:
«волшебный» мешочек;
для каждой группы из четырех человек: карточки размером 14 формата А4 с отмеченными на них тремя взаимосвязанными числами для составления примеров и карточка для записи примеров;
для каждого учащегося: картонные карточки домино с точками.
Критерии успеха
Ответ
Один пример, так как складываются одинаковые числа.
5+ 5 = 10
10-5 = 5
Конец урока
Реши. В задание включены примеры на сложение и вычитание однозначных чисел с переходом через десяток. Данное задание дано в качестве дифференциации, его выполнение предложите высокомотивированным учащимся. Применяя знания о взаимосвязи действий сложения и вычитания, первоклассникам необходимо будет решить предложенные примеры.
Критерии успеха
Ответы
11-2 = 9;
11-9 = 2.
Дифференциация
Каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?
Оценивание
Как Вы планируете проверить уровень усвоения материала учащимися?
Используйте данный раздел для записи методов, которые Вы будете использовать для оценивания того, чему учащиеся научились во время урока.
Здоровье и соблюдение техники безопасностиЗдоровьесберегающие технологии.
Используемые физминутки и активные виды деятельности.
Собери пазлы. Задание основано на принципе игры в пазлы и направлено на отработку навыка составления четырех взаимосвязанных примеров. Ребята должны собрать пазл из частей, соединяя части головоломки с помощью стрелок, как показано на образце. Рядом с пазлом нужно записать четыре взаимосвязанных примера, соответствующих изображениям на пазлах.
Заполни кости домино. Задание основано на принципе игры в лото. В ходе выполнения задания дети должны установить взаимосвязь между записанными на карточках выражениями и дописать недостающие выражения. В итоге на каждой карточке должно быть записано по четыре примера: два на сложение и два обратных — на вычитание.
Рассмотри узор мозаики. Учащиеся смогут составить по четыре примера с опорой на количество цветных квадратов для составления узора мозаики. Вторая часть задания направлена на развитие творческих способностей. В этом случае школьники смогут составить свой узор мозаики, используя два цвета, затем записать к нему четыре примера.
Для закрепления вывода о взаимосвязи действий сложения и вычитания продолжите работу в парах. Познакомьте детей с игрой в домино. Предупредите, что на уроке правила игры будут немного изменены.
Каждая пара получает по одной кости домино и составляет четверки взаимосвязанных примеров (два на сложение и два на вычитание). Взаимопроверка осуществляется между парами в группе. Если в ходе работы учащиеся допустили ошибки, состав пар меняется внутри одной группы, и работа повторяется. Если группа успешно справляется с работой, ребята поднимают руки вверх, что является сигналом о завершении работы.
К концу урока учащиеся научатся:
—устанавливать взаимосвязь действий сложения и вычитания;
—составлять четверки взаимосвязанных примеров. Чтобы оценить, как школьники усвоили тему урока, дайте им следующие задания:
—Дан пример: 3 + 2 = 5. Составьте к нему обратные примеры.
—Дан пример: 9-6 = 3. Составьте к нему обратные примеры.
Задайте вопрос: «Как связаны действия сложения и вычитания?».
Организуйте самооценивание учащихся с помощью «Лестницы успеха» в рабочей тетради.
Динамическая пауза.
Мы шли, шли, шли
Землянику нашли.
Раз, два, три, четыре, пять
Мы идём искать опять.
Источник
- Главная
- Вопросы & Ответы
- Вопрос 3842996
более месяца назад
Просмотров : 9
Ответов : 1
Лучший ответ:

А) 168-(х+47)=168-х-47=168-47-х=121-х
б) 384-m-137=384-137-m=247-m
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи:































Другие вопросы:
1)чем объясняется превращение Западной Европы в крупнейший в мире регион притяжения рабочей силы извне?2)почему именно Роттердам стал одним из крупнейших портов мира по грузообороту?
более месяца назад
Смотреть ответ
Просмотров : 11
Ответов : 1
Помогите еще решить пожалуйста С1
более месяца назад
Смотреть ответ
Просмотров : 8
Ответов : 1
7 Клас математика решите пожалуйста
более месяца назад
Смотреть ответ
Просмотров : 6
Ответов : 1
Почему водоемы не промерзают до дна?
более месяца назад
Смотреть ответ
Просмотров : 11
Ответов : 1
Сочинение о верблюде по английскому языку
более месяца назад
Смотреть ответ
Просмотров : 11
Ответов : 1
Источник
