Какие свойства сложение ответ

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта

Вопросы к параграфу

1. Как в равенстве а + b = с называют число а? Число b? Число с? Выражение а + b?

• a — слагаемое
• b — слагаемое
• c — сумма
• a+b — сумма

2. Сформулируйте переместительное свойство сложения.

От перестановки слагаемых сумма не меняется.

3. Как записывают в буквенном виде переместительное свойство сложения?

а + b = b + а

4. Сформулируйте сочетательное свойство сложения.

Чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего.

5. Как записывают в буквенном виде сочетательное свойство сложения?

(a + b) + c = a + (b + c)

6. Каким свойством обладает число 0 при сложении?

Если одно из двух слагаемых равно 0, то сумма равна другому слагаемому.

Решаем устно

1. Вычислите:

1. 23 + 17 = 40
2. 230 + 17 = 247
3. 23 + 170 = 193
4. 30 — 13 = 17
5. 300 — 130 = 170
6. 300 — 13 = 287
7. 12 • 4 = 48
8. 12 • 40 = 480
9. 120 • 40 = 4800
10. 72 : 8 = 9
11. 720 : 8 = 90
12. 720 : 80 = 9

2. Назовите два последовательных натуральных числа, сумма которых равна 91.

Любые два последовательных натуральных числа различаются между собой на 1. 

1) 90 — 1 = 90 — сумма искомых натуральных чисел без различающих их 1.

2) 90 : 2 = 45 — наименьшее из искомых натуральных чисел.

3) 45 + 1 = 46 — наибольшее из искомых натуральных чисел.

Ответ: 45 и 46.

3. Назовите двузначное число, сумма цифр которого равна наибольшему однозначному числу. Сколько существует таких чисел?

Наибольшее двузначное число — 9.

Значит условию удовлетворяют следующие двузначные числа: 18, 81, 27, 72, 36, 63, 45, 54, 90. Значит существует 9 таких чисел.

Упражнения

167. Найдите сумму:

168. Выполните сложение:

169. Аня и Коля решали задачи. Коля решил 26 задач, а Аня — на 16 задач больше. Сколько задач решили Коля и Аня вместе?

1) 26 + 16 = 42 (задачи) — решила Аня.

2) 42 + 26 = 68 (задач) — решили Коля и Аня вместе.

Ответ: 68 задач.

170. Миша купил книгу за 170 р., что на 12 р. меньше, чем заплатил Петя за свою новую книгу. Сколько рублей заплатили за книги Миша и Петя вместе?

1) 170 + 12 = 182 (рубля) — заплатил за книгу Петя.

2) 170 + 182 = 352 (рубля) — заплатили за свои книги Петя и Миша вместе.

Ответ: 352 рубля.

171. Выполните сложение, выбирая удобный порядок вычислений:

1. (42 + 37) + 58 = (42 + 58) + 37 = 100 + 37 = 137
2. 29 + (98 + 71) = (29 + 71) + 98 = 100 + 98 = 198
3. (215 + 818) + 785 = (215 + 785) + 818 = 1 000 + 818 = 1 818
4. 634 + (458 + 166) = (634 + 166) + 458 = 800 + 458 = 1 258
5. 183 + 732 + 268 + 317 = (183 + 317) + (732 + 268) = 500 + 1 000 = 1 500
6. 339 + 584 + 416 + 661 = (339 + 661) + (584 + 416) = 1 000 + 1 000 = 2 000
7. (15 083 + 1 458) + (4 917 + 6 542) = (15 083 + 4 917) + (1 458 + 6 542) = 20 000+ 8 000 = 28 000
8. (1 654 + 18 135) + (7 346 + 11 865) = (1 654 + 7 346) + (18 135 + 11 865) = 9 000 + 30 000 = 39 000

172. Используйте свойства сложения при вычислении суммы:

1. (146 + 322) + 178 (322 + 178) + 146 = 500 + 146 = 646
2. 784 + (179 + 116) = (784 + 116) + 179 = 900 + 179 = 1 079
3. 625 + 481 + 75 + 219 = (625 + 75) + (481 + 219) = 700 + 700 = 1 400
4. 427 + 88 + 273 + 112 = (427 + 273) + (88 + 112) = 700 + 200 = 900

173. Стена Московского Кремля состоит из трёх участков: южного, восточного и западного. Длина южного участка составляет 685 м, что на 45 м меньше длины восточного. Длина западного участка на 135 м больше длины южного. Сколько метров составляет общая длина стен Московского Кремля?

1) 685 + 45 = 730 (метров) — длина восточной стены Кремля.

2) 685 + 135 = 820 (метров) — длина Западной стены Кремля.

3) 685 + 730 + 820 = 2 235 (метров) — общая длина стен Кремля.

Ответ: 2 235 метров.

174. У Иры в коллекции есть 26 марок, посвящённых историческим событиям, а также марки, посвящённые архитектуре и спорту. Марок по архитектуре у неё на 15 больше, чем по истории, и на 14 меньше, чем на спортивную тему. Сколько марок в коллекции у Иры?

1) 26 + 15 = 41 (марки) — по архитектуре.

2) 41 + 14 = 55 (марок) — посвящённых спорту.

3) 26 + 41 + 55 = 122 (марки) — всего в коллекции Иры.

Ответ: 122 марки.

175. На одной полке было 17 книг, на второй — на 18 книг больше, чем на первой, а на третьей — на 6 книг больше, чем на первой и второй вместе. Сколько всего книг было на трёх полках?

1) 17 + 18 = 35 (книг) — на второй полке.

2) 35 + 17 = 52 (книги) — на первой и второй полке вместе.

3) 52 + 6 = 58 (книг) — на третьей полке.

4) 52 + 58 = 110 (книг) всего на трёх полках.

Ответ: 110 книг.

176. Отправившись в велосипедный поход, группа туристов в первый день проехала 42 км, что на 12 км меньше, чем во второй, а в третий — на 4 км больше, чем в первый и второй вместе. Сколько километров проехали туристы за три дня?

1) 42 + 12 = 54 (км) — туристы проехали во второй день.

2) 42 + 54 = 96 (км) — туристы проехали всего за первый и второй день.

3) 96 + 4 = 100 (км) — туристы проехали в третий день.

4) 96 + 100 = 196 (км) — туристы проехали за три дня всего.

Ответ: 196 км.

177. Упростите выражение:

1. (74 + x) + 38 = (74 + 38) + x = 112 + x
2. 238 + (а + 416) = (238 + 416) + a = 654 + a
3. у + 324 + 546 = y + (325 + 546) = y + 870
4. 2 753 + m + 4 199 = (2 753 + 4 199) + m = 6 952 + m
5. (b + 457) + (143 + 872) = b + (457 + 143) + 872 = b + 600 + 872 = b + 1 472
6. (2 235 + с) + (4 671 + 1 765) = (2 235 + 1 765) + c + 4 671 = (4 000 + 4 671) + c = 8 671 + c
7. (1 696 + 3 593) + (р + 1 304) = (1 696 + 1 304) + 3 593 + p = (3 000 + 3 593) + p = 6 593 + p
8. (5 432 + 8 951) + (4 568 + а + 1 049) = (5 432 + 4 568) + (8 951 + 1 049) + a = (10 000 + 10 000) + a = 20 000 + a

178. Упростите выражение:

1. (56 + а) + 14 = (56 + 14) + a = 70 + a
2. 342 + (b + 58) = (342 + 58) + b = 400 + b
3. 805 + х + 195 = (805 + 195) + x = 1 000 + x
4. m + 4 563 + 1 837 = m + (4 563 + 1 837) = m + 6 400

179. Дядя Фёдор выехал из города в Простоквашино в 15 ч 40 мин и потратил на дорогу 3 ч 50 мин. В котором часу дядя Фёдор приехал в Простоквашино?

1) 15 ч 40 мин + 3 ч 50 мин = (15 ч + 3 ч) + (40 мин + 50 мин) = 18 ч + 90 мин = 18 ч + (60 мин + 30 мин) = (18 ч + 1 ч) + 30 мин = 19 ч 30 мин

Ответ: дядя Фёдор приехал в Простоквашино в 19 часов 30 минут.

180. Поезд отправляется от станции А в 9 ч 57 мин и прибывает на станцию В через 2 ч 36 мин. В котором часу поезд прибывает на станцию В?

1) 9 ч 57 мин + 2 ч 36 мин = (9 ч + 2 ч) + ( 57 мин + 36 мин) = 11 ч + 93 мин = 11 ч + (60 мин + 33 мин) = (11 ч + 1 ч) + 33 мин = 12 ч 33 мин

Ответ: поезд прибывает на станцию В в 12 часов 33 минуты.

181. Найди:

1. Как изменится сумма, если одно из слагаемых увеличить на 12? Сумма увеличится на 12.
2. Как изменится сумма, если одно из слагаемых увеличить на 23, а второе — на 17? Сумма увеличится на 40 (23 + 17 = 40).
3. Как изменится сумма, если одно из слагаемых уменьшить на 34? Сумма уменьшится на 34.
4. Как изменится сумма, если одно из слагаемых уменьшить на 16, а второе — на 9? Сумма уменьшится на 25 (16 + 9 = 25).
5. Как изменится сумма, если одно из слагаемых увеличить на 28, а второе уменьшить на 15? Сумма увеличится на 13 (28 — 15 = 13).
6. Одно из слагаемых увеличили на 3. На сколько надо увеличить второе слагаемое, чтобы сумма увеличилась на 14? Второе слагаемое надо увеличить на 11 (14 — 3 = 11).
7. Одно из слагаемых увеличили на 8. Как надо изменить второе слагаемое, чтобы сумма:
   • а) увеличилась на 3 — Надо второе слагаемое уменьшить на 5 (8 — 5 = 3).
   • б) уменьшилась на 5 — Надо второе слагаемое уменьшить на 13 (13 — 8 = 5). 

182. Найдите сумму:

1. 76 м 39 см + 41 м 58 см = (76 м + 41 м) + (39 см + 58 см) = 117 м + 97 см = 117 м 97 см
2. 4 км 238 м + 3 км 474 м = (4 км + 3 км) + (238 м + 474 м) = 7 км + 712 м = 7 км 712 м
3. 64 м 86 см + 27 м 45 см = (64 м + 27 м) + (86 см + 45 см) = 91 м + 131 см = 91 м + (100 см + 31 см) = (91 м + 1 м) + 31 см = 92 м 31 см
4. 16 км 527 м + 37 км 783 м = (16 км + 37 км) + (6 527 м + 783 м) = 53 км + 1 310 м = 53 км + (1 000 м + 310 м) = (53 км + 1 км) + 310 м = 54 км 310 м
5. 12 ч 24 мин + 9 ч 18 мин = (12 ч + 9 ч) + (24 мин + 18 мин) = 21 ч + 42 мин = 21 ч 42 мин
6. 35 мин 17 с + 16 мин 35 с = (35 мин + 16 мин) + (17 с + 35 с) = 51 мин + 52 с = 51 мин 52 с
7. 18 ч 42 мин + 14 ч 29 мин = (18 ч + 14 ч) + (42 мин + 29 мин) = 32 ч + 71 мин = 32 ч + (60 мин + 11 мин) = (32 ч + 1 ч) + 11 мин = 33 ч 11 мин
8. 53 мин 32 с + 44 мин 56 с = (53 мин + 44 мин) + (32 с + 56 с) = 97 мин + 88 с = (60 мин + 37 мин) + (60 с + 28 с) = 1 ч + (37 мин + 1 мин) + 28 с = 1 ч 38 мин 28 с

183. Найдите сумму:

1. 4 дм 6 см + 5 дм 8 см = (4 дм + 5 дм) + (6 см + 8 см) = 9 дм + 14 см = 9 дм + (10 см + 4 см) = (9 дм + 1 дм) + 4 см = 10 дм 4 см
2. 8 м 5 см + 6 м 96 см = (8 м + 6 м) + (5 см + 96 см) = 14 м + 101 см = 14 м + (100 см + 1 см) = (14 м + 1 м) + 1 см = 15 м 1 см
3. 12 км 29 м + 24 км 92 м = (12 км + 24 км) + (29 м + 92 м) = 36 км 121 м
4. 2 т 4 ц 56 кг + 9 т 6 ц 48 кг = (2 т + 9 т) + (4 ц + 6 ц) + (56 кг + 48 кг) = 11 т + 10 ц +104 кг = (11 т + 1 т) + (100 кг + 4 кг) = 12 т + 1 ц + 4 кг = 12 т 1 ц 4 кг
5. 3 ч 48 мин + 2 ч 26 мин = (3 ч + 2 ч) + (48 мин + 26 мин) = 5 ч + 74 мин = 5 ч + (60 мин + 14 мин) = (5 ч + 1 ч) + 14 мин = 6 ч 14 мин
6. 25 мин 17 с + 7 мин 54 с = (25 мин + 7 мин) + (17 с + 54 с) =32 мин + 71 с = 32 мин + (60 с + 11 с) = (32 мин + 1 мин) + 11 с = 33 мин + 11 с

184. Вместо звёздочек поставьте цифры так, чтобы сложение было выполнено верно:

185. Вместо звёздочек поставьте цифры так, чтобы сложение было выполнено верно:

186. Не выполняя вычислений, расположите данные суммы в порядке возрастания:

1. 129 + 288
2. 288 + 659
3. 782 + 659
4. 782 + 943
5. 943 + 1 105
6. 1 105 + 2 563

187. Найдите сумму наиболее удобным способом:

1) 1 + 2 + 3 + … + 9 + 10

1 + 2 + 3 + … + 9 + 10 = (1 + 9) + (2 + 8) + (3 + 7) + (4 + 6) + 5 + 10 = 10 + 10 + 10 + 10 + 5 + 10 = 10 • 4 + 5 + 10 = 40 + 5 + 10 = 55

Комментарий: В данном примере надо сложить 11 чисел. из них:

• есть один десяток
• четыре пары образуют десяток
• число 5

В результате получаем 5 десятков плюс 5, то есть число 55.

2) 1 + 2 + 3 + … + 99 + 100

1 + 2 + 3 + … + 99 + 100 = (1 + 99) + (2 + 98) + (3 + 97) + … + (49 + 51) + 50 + 100 = 100 • 49 + 50 + 100 = 4900 + 50 + 100 = 5 500.

188. Найди:

1) На сколько сумма 1 + 3 + 5 + … + 99 меньше, чем сумма 2 + 4 + 6 + … + 100?

1) 1 + 3 + 5 + … + 99 = (1 + 99) + (3 + 97) + (5 + 95) + … + (49 + 51) = 100 • 25 = 2 500 — слагаемыми являются только нечётные числа, а от 1 до 49 их 25 штук.

2) 2 + 4 + 6 + … + 100 = (2 + 98) + (4 + 96) + (6 + 94) + … + (48 + 52) + 50 + 100 = 100 • 24 + 50 + 100 = 2 400 + 50 + 100 = 2 550 — слагаемыми являются только нечётные числа, а их 24 пары по 100 плюс число 50 плюс число 100.

3) 2 550 — 2 500 = 50

Ответ: на 50.

2) Какая из сумм 1 + 3 + 5 + … + 2 001 и 2 + 4 + 6 + … + 2 000 больше и на сколько?

1) 1 + 3 + 5 + … + 2 001 = (1 + 1 999) + (3 + 1997) + (5 + 1995) + … + (999 + 1 001) + 2 001 = 2 000 • 500 + 2 001 = 1 000 000 + 2 001 = 1 002 001

2) 2 + 4+ 6 + … + 2 000 = (2 + 1998) + (4 + 1996) + (6 + 1994) + … + (998 + 1 002) + 1 000 + 2 000 = 2 000 • 490 + 1 000 + 2 000 = 2 000 + 500 + 1 000 = 1 000 000 + 1 000 = 1 001 000

3) 1 002 001 — 1 001 000 = 1 001

Ответ: сумма 1 + 3 + 5 + … + 2 001 больше суммы 2 + 4 + 6 + … + 2 000 на 1 001.

189. В записи 4 4 4 4 4 4 4 4 поставьте между некоторыми цифрами знак «+» так, чтобы получилось выражение, значение которого равно 500.

444 + 44 + 4 + 4 + 4 = (444 + 44) + (4 + 4 + 4) = 488 + 12 = 500

Ответ: 444 + 44 + 4 + 4 + 4

190. Замените звёздочки числами так, чтобы сумма любых трёх соседних чисел была равна 20:  7,  *,  *,  *,  *,  *,  *,  9.

7, 9 , 4, 7, 9, 4, 7, 9

7 + 9 + 5 = 20; 9 + 4 + 7 = 20; 4 + 7 + 9 = 20 и т.д.

Ответ: 7, 9 , 4, 7, 9, 4, 7, 9.

191. Слава разрезал проволоку на кусочки и составил фигуру, изображённую на рисунке 65. Мог ли Слава разрезать эту же проволоку так, чтобы составить фигуру, изображённую на рисунке 66?

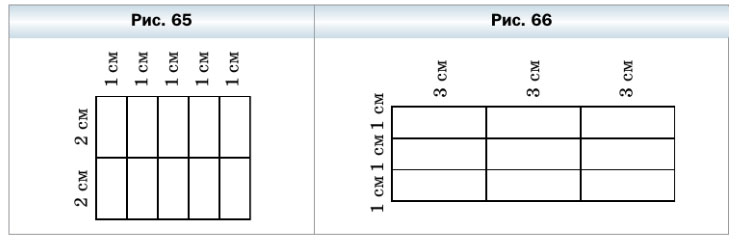
Посчитаем, сколько проволоки Слава потратил на составление первой фигуры:

• 15 кусочков по 1 см
• 12 кусочков по 2 см

1) 15 • 1 + 12 • 2 = 15 + 24 = 39 (см) — проволоки использовано на первую фигуру.

Посчитаем, сколько проволоки Славе потребуется для составления второй фигуры:

• 12 кусочков по 3 см
• 12 кусочков по 1 см

2) 12 • 3 + 12 • 1 = 36 + 12 = 48 (см) — проволоки потребуется для второй фигуры.

3) 39 < 48, значит проволоки с первой фигуры не хватит для изготовления второй фигуры.

Ответ: нет, длины проволоки, использованной для первой фигуры, не хватит для изготовления второй фигуры.

Упражнения для повторения

192. Отметьте на координатном луче натуральные числа, которые больше 6, но меньше 12.

193. Запишите все шестизначные числа, которые больше 999 888 и оканчиваются цифрой 5.

• 999 895
• 999 905
• 999 915
• 999 925
• 999 935
• 999 945
• 999 955
• 999 965
• 999 975
• 999 985
• 999 995

194. Скороход прошёл 24 км за 4 ч. На обратном пути он увеличил скорость на 2 км/ч. Сколько времени он потратил на обратный путь?

1) 24 : 4 = 6 (км/ч) — скорость движения скорохода по пути туда.

2) 6 + 2 = 8 (км/ч) — скорость движения скорохода по пути обратно.

3) 24 : 8 = 3 (часа) — скороход потратил на обратный путь.

Ответ: 3 часа.

195. Вася старше своей сестры Светы на 5 лет. На сколько лет он будет старше Светы через 7 лет?

И через 7 лет, и через 10, и через любое количество лет разница в возрасте между Васей и Светой останется одинаковой — 5 лет. Это происходит потому, что с количество лет прибавляется с каждым годом для всех с одинаковой скоростью.

Ответ: Вася будет старше своей сестры Светы на 5 лет.

Задача от мудрой совы

196. Можно ли таблицу из пяти строк и шести столбцов заполнить натуральными числами так, чтобы сумма чисел каждой строки была равна 30, а сумма чисел каждого столбца — 20?

Мы знаем, что строк в таблице должно быть 5 и сумма натуральных чисел в каждой строке должна равняться 30. Значит сумма натуральных числе во всех пяти строках таблицы должна равняться:

1) 30 • 5 = 150

Мы знаем, что столбцов с таблице должно быть 6 и сумма всех натуральных чисел в каждом столбце таблицы должна равняться 20. Значит сумма натуральных числе во всех шести столбцах таблицы должна равняться:

2) 20 • 6 = 120

Получается, что сумма натуральных чисел в таблице, если считать по строкам и если считать по столбцам, не совпадает:

3) 150 ≠ 120

Значит таблицу с указанными условиями невозможно заполнить натуральными числами.

Ответ: нет, такую таблицу заполнить невозможно.

• Ответы к учебнику для 5 класса. А. Г. Мерзляк
• Переход на главную страницу сайта