Какие свойства синус косинус
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство – знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство – периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: “угол первой, второй, третьей или четвертой координатной четверти”. Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
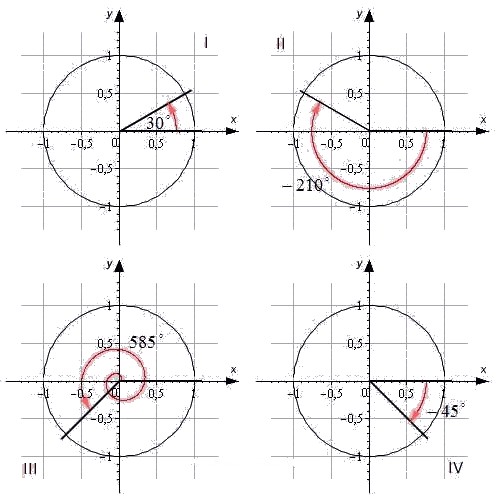
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° – угол третьей четверти. Угол -45° – это угол четвертой четверти.
При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
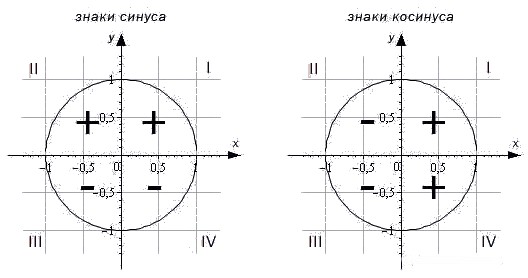
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус – это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной – отрицательна.
Косинус – это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
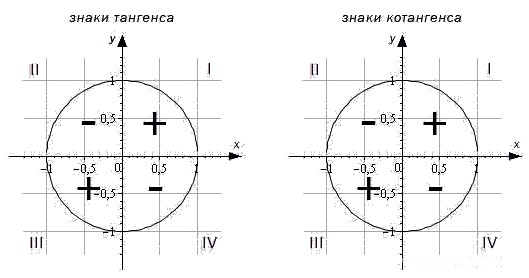
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс – отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки – отрицательным. Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус – в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус – в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус – в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус – в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности – одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin13π5=sin3π5+2π=sin3π5
tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
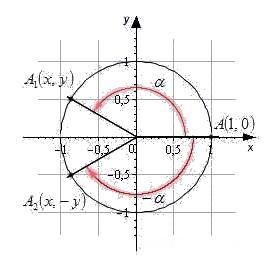
Точка A1(x, y) – результат поворота начальной точки A0(1, 0) вокруг центра окружности на угол α. Точка A2(x, -y) – результат поворота начальной точки на угол -α.
Точки A1и A2 симметричны относительно оси абсцисс. В случае, когда α=0°, ±180°, ±360° точки A1и A2 совпадают. Пусть одна точка имеет координаты (x, y), а вторая – (x, -y). Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α=y, cos α=x, tg α=yx, ctg α=xysin-α=-y, cos-α=x, tg-α=-yx, ctg-α=x-y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin-α=-sin αcos-α=cos αtg-α=-tg αctg-α=-ctg α
Согласно этому свойству, справедливы равенства
sin-48°=-sin 48°, ctgπ9=-ctg-π9, cos 18°=cos-18°
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Источник
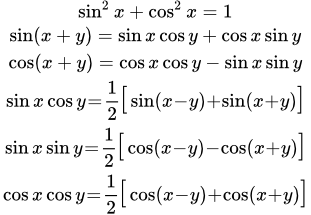
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Содержание
Геометрическое определение синуса и косинусаПринятые обозначенияГрафики функций синус, y = sin x, и косинус, y = cos xСвойства синуса и косинусаПериодичностьЧетностьОбласть определения и значений, экстремумы, возрастание, убываниеОсновные формулыСумма квадратов синуса и косинусаФормулы синуса и косинуса от суммы и разностиФормулы произведения синусов и косинусовФормулы суммы и разностиВыражение синуса через косинусВыражение косинуса через синусВыражение через тангенсТаблица синусов и косинусов, тангенсов и котангенсовВыражения через комплексные переменныеФормула ЭйлераВыражения через гиперболические функцииПроизводныеИнтегралыРазложения в рядыСеканс, косекансОбратные функцииАрксинус, arcsinАрккосинус, arccosСм. также: Тангенс, котангенс, свойства, графики, формулы
Обратные тригонометрические функции, их графики и формулы
Геометрическое определение синуса и косинуса
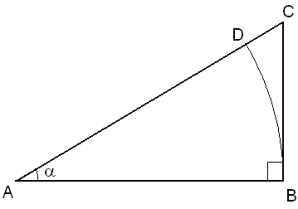Прямоугольный треугольник.
|BD| – длина дуги окружности с центром в точке A.
α – угол, выраженный в радианах.
Синус (sin α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
Графики функций синус, y = sin x, и косинус, y = cos x
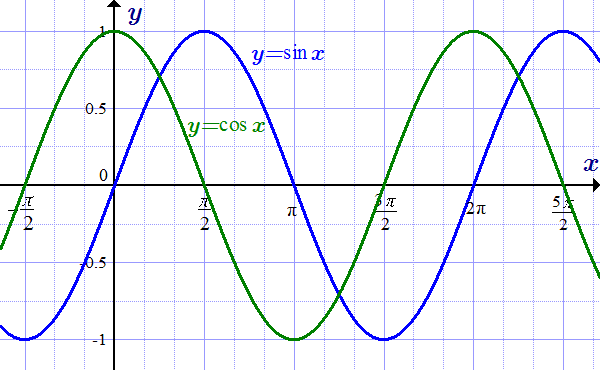Графики функций y=sin(x) и y=cos(x).
Графики синуса и косинуса смещены по оси x друг относительно друга на :
.
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
Четность
Функция синус – нечетная. Функция косинус – четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n – целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | –1 ≤ y ≤ 1 | –1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = –1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
Далее мы полагаем, что – целое число.
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При , имеем:
; .
При :
; .
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.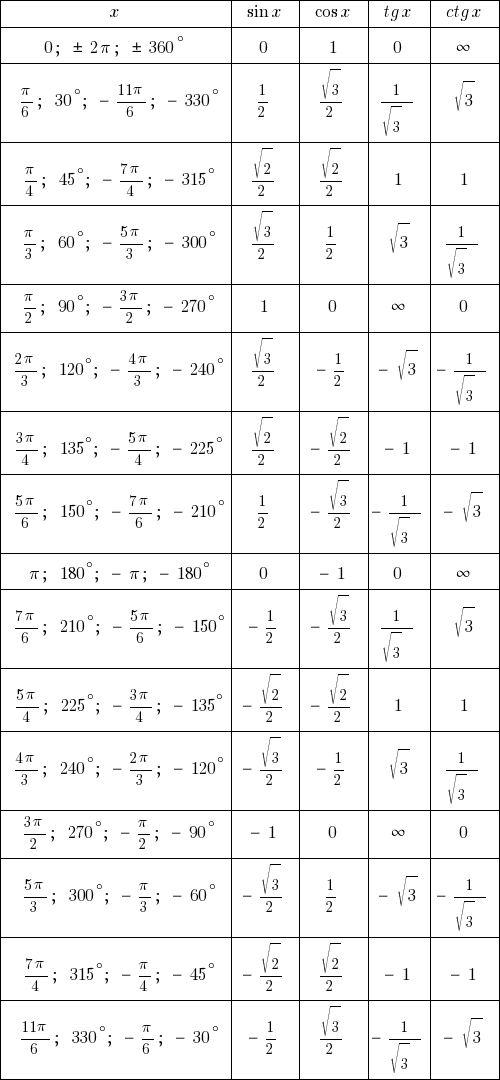 
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
; .
Интегралы
;
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
{ –∞ < x < +∞ }
{ –∞ < x < +∞ }
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: 15-02-2014 Изменено: 10-05-2020
См. также: Тангенс, котангенс, свойства, графики, формулы
Обратные тригонометрические функции, их графики и формулы
Источник
- Главная
- Справочник
- Тригонометрия
- Синус (sin x) и косинус (cos x) – свойства, графики, формулы
Геометрическое определение синуса и косинуса
( sin alpha = dfrac{|BC|}{|AB|} ), ( cos alpha = dfrac{|AC|}{|AB|} )
α – угол, выраженный в радианах.
Синус (sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AB|.
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AC| к длине гипотенузы |AB|.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла – это абсцисса точки. Синус угла – это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
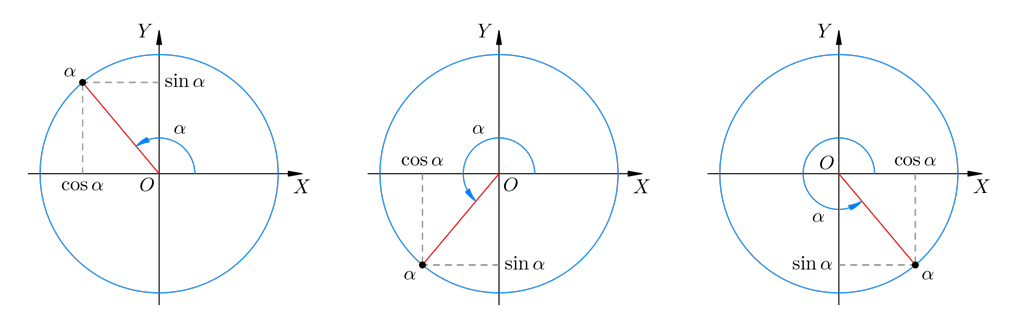
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Нулевой угол ( LARGE 0^{circ } )
Абсцисса точки 0 равна 1, ордината точки 0 равна 0. Следовательно,
cos 0 = 1 sin 0 = 0
Рис 4. Нулевой угол
Угол ( LARGE frac{pi}{6} = 30^{circ } )
Мы видим прямоугольный треугольник с единичной гипотенузой и острым углом 30°. Как известно, катет, лежащий напротив угла 30°, равен половине гипотенузы1; иными словами, вертикальный катет равен 1/2 и, стало быть,
[ sin frac{pi}{6} =frac{1}{2} ]
Горизонтальный катет находим по теореме Пифагора (или, что то же самое, находим косинус по основному тригонометрическому тождеству):
[ cos frac{pi}{6} = sqrt{1 – left(frac{1}{2} right)^{2} } =frac{sqrt{3} }{2} ]
1 Почему так получается? Разрежьте равносторонний треугольник со стороной 2 вдоль его высоты! Он распадётся на два прямоугольных треугольника с гипотенузой 2, острым углом 30° и меньшим катетом 1.
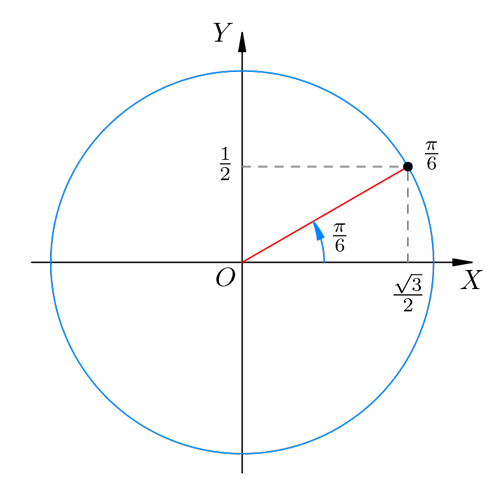
Рис 5. Угол π / 6
Угол ( LARGE frac{pi}{4} = 45^{circ } )
В данном случае прямоугольный треугольник является равнобедренным; синус и косинус угла 45° равны друг другу. Обозначим их пока через x. Имеем:
[ x^{2} + x^{2} = 1 ]
откуда ( x=frac{sqrt{2} }{2} ). Следовательно,
[ cos frac{pi}{4} = sin frac{pi}{4} =frac{sqrt{2} }{2} ]
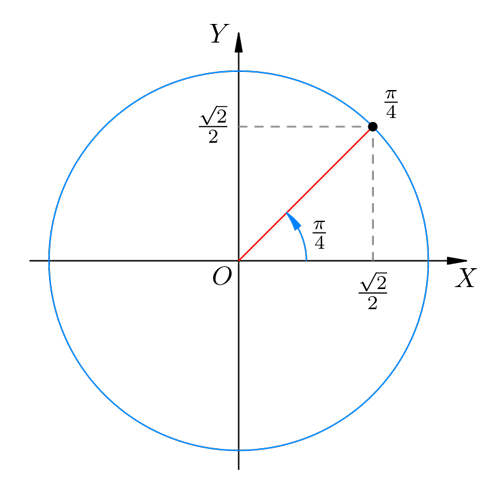
Рис 5. Угол π / 4
Свойства синуса и косинуса
Принятые обозначения
( sin^2 x equiv (sin x)^2; )( quad sin^3 x equiv (sin x)^3; )( quad sin^n x equiv (sin x)^n )( sin^{-1} x equiv arcsin x )( (sin x )^{-1} equiv dfrac1{sin x} equiv cosec x ).
( cos^2 x equiv (cos x)^2; )( quad cos^3 x equiv (cos x)^3; )( quad cos^n x equiv (cos x)^n )( cos^{-1} x equiv arccos x )( (cos x )^{-1} equiv dfrac1{cos x} equiv sec x ).
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
( sin(x + 2pi) = sin x; quad )( cos(x + 2pi) = cos x )
Четность
Функция синус – нечетная. Функция косинус – четная.
( sin( -x ) = – sin x; quad )( cos( -x ) = cos x )
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n – целое).
| ( small -dfrac{pi}2 + 2pi n )( small < x < )( small dfrac{pi}2 + 2pi n ) | ( small -pi + 2pi n )( small < x < )( small 2pi n ) | |
| Убывание | ( small dfrac{pi}2 + 2pi n )( small < x < )( small dfrac{3pi}2 + 2pi n ) | ( small 2pi n )( small < x < )( pi + small 2pi n ) |
| Максимумы, ( small x = )( small dfrac{pi}2 + 2pi n ) | ( small x = 2pi n ) | |
| Минимумы, ( small x = )( small -dfrac{pi}2 + 2pi n ) | ( small x = )( small pi + 2pi n ) | |
| Нули, ( small x = pi n ) | ( small x = dfrac{pi}2 + pi n ) | |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы, содержащие синус и косинус
Сумма квадратов
( sin^2 x + cos^2 x = 1 )
Формулы синуса и косинуса суммы и разности
( sin(x + y) = sin x cos y + cos x sin y )
( sin(x – y) = sin x cos y – cos x sin y )
( cos(x + y) = cos x cos y – sin x sin y )
( cos(x – y) = cos x cos y + sin x sin y )
( sin( 2x ) = 2 sin x cos x )
( cos( 2x ) = cos^2 x – sin^2 x = )( 2 cos^2 x – 1 = 1 – 2 sin^2 x )
( cosleft( dfrac{pi}2 – x right) = sin x ) ; ( sinleft( dfrac{pi}2 – x right) = cos x )
( cos( x + pi ) = – cos x ) ; ( sin( x + pi ) = – sin x )
Формулы произведения синусов и косинусов
( sin x cos y = )( dfrac12 {Large [} sin( x – y ) + sin( x + y ) {Large ]} )
( sin x sin y = )( dfrac12 {Large [} cos( x – y ) – cos( x + y ) {Large ]} )
( cos x cos y = )( dfrac12 {Large [} cos( x – y ) + cos( x + y ) {Large ]} )
( sin x cos y = dfrac12 sin 2x )
( sin^2 x = dfrac12 {Large [} 1 – cos 2x {Large ]} )
( cos^2 x = dfrac12 {Large [} 1 + cos 2x {Large ]} )
Формулы суммы и разности
( sin x + sin y = 2 , sin dfrac{x+y}2 , cos dfrac{x-y}2 )
( sin x – sin y = 2 , sin dfrac{x-y}2 , cos dfrac{x+y}2 )
( cos x + cos y = 2 , cos dfrac{x+y}2 , cos dfrac{x-y}2 )
( cos x – cos y = 2 , sin dfrac{x+y}2 , sin dfrac{y-x}2 )
Выражение синуса через косинус
Далее мы полагаем, что ( n ) – целое число.
( sin x = cosleft( dfrac{pi}2 – x right) = )( cosleft( x – dfrac{pi}2 right) = – cosleft( x + dfrac{pi}2 right) )( sin^2 x = 1 – cos^2 x )( sin x = sqrt{1 – cos^2 x} ) ( { 2 pi n leqslant x leqslant pi + 2 pi n } )( sin x = – sqrt{1 – cos^2 x} ) ( { -pi + 2 pi n leqslant x leqslant 2 pi n } ).
Выражение косинуса через синус
( cos x = sinleft( dfrac{pi}2 – x right) = )( – sinleft( x – dfrac{pi}2 right) = sinleft( x + dfrac{pi}2 right) )( cos^2 x = 1 – sin^2 x )( cos x = sqrt{1 – sin^2 x} ) ( { -pi/2 + 2 pi n leqslant x leqslant pi/2 + 2 pi n } )( cos x = – sqrt{1 – sin^2 x} ) ( { pi/2 + 2 pi n leqslant x leqslant 3pi/2 + 2 pi n } ).
Выражение через тангенс
( sin^2 x = dfrac{tg^2 x}{1+tg^2 x} )( cos^2 x = dfrac1{1+tg^2 x} ).
При ( – dfrac{pi}2 + 2 pi n < x < dfrac{pi}2 + 2 pi n )( sin x = dfrac{tg x}{ sqrt{1+tg^2 x} } )( cos x = dfrac1{ sqrt{1+tg^2 x} } ).
При ( dfrac{pi}2 + 2 pi n < x < dfrac{3pi}2 + 2 pi n ) :
( sin x = – dfrac{tg x}{ sqrt{1+tg^2 x} } )( cos x = – dfrac1{ sqrt{1+tg^2 x} } ).
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style=”max-width:500px;max-height:1080px;” src=”tablitsa.png” alt=”Таблица синусов и косинусов” title=”Таблица синусов и косинусов” ]
Выражения через комплексные переменные
( i^2 = -1 )
( sin z = dfrac{e^{iz} – e^{-iz}}{2i} )( cos z = dfrac{e^{iz} + e^{-iz}}{2} )
Формула Эйлера
( e^{iz} = cos z + i sin z )
Выражения через гиперболические функции
( sin iz = i sh z )( cos iz = ch z )
( sh iz = i sin z )( ch iz = cos z )
Производные
( ( sin x )’ = cos x )( ( cos x )’ = – sin x ). Вывод формул > > >
Производные n-го порядка:
( left( sin x right)^{(n)} = sinleft( x + ndfrac{pi}2 right) )( left( cos x right)^{(n)} = cosleft( x + ndfrac{pi}2 right) ).
Интегралы
( int sin x , dx = – cos x + C )( int cos x , dx = sin x + C )
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
( sin x = sum_{n=0}^{infty} dfrac{ (-1)^n x^{2n+1} }{ (2n+1)! } = )( x – dfrac{x^3}{3!} + dfrac{x^5}{5!} – dfrac{x^7}{7!} + … ) ( {- infty < x < infty } )
( cos x = sum_{n=0}^{infty} dfrac{ (-1)^n x^{2n} }{ (2n)! } = )( 1 – dfrac{x^2}{2!} + dfrac{x^4}{4!} – dfrac{x^6}{6!} + … ) ( { – infty < x < infty } )
Секанс, косеканс
( sec x = dfrac1{ cos x } ; ) ( cosec x = dfrac1{ sin x } )
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
( y = arcsin x ) ( left{ -1 leqslant x leqslant 1; ; – dfrac{pi}2 leqslant y leqslant dfrac{pi}2 right} )
( sin( arcsin x ) = x ) ( { -1 leqslant x leqslant 1 } )
( arcsin( sin x ) = x ) ( left{ – dfrac{pi}2 leqslant x leqslant dfrac{pi}2 right} )
Арккосинус, arccos
( y = arccos x ) ( left{ -1 leqslant x leqslant 1; ; 0 leqslant y leqslant pi right} )
( cos( arccos x ) = x ) ( { -1 leqslant x leqslant 1 } )
( arccos( cos x ) = x ) ( { 0 leqslant x leqslant pi } )
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Источник
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cosα) – отношение прилежащего катета к гипотенузе.
Тангенс угла (tg α) – отношение противолежащего катета к прилежащему.
Котангенс угла (ctg α) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от -∞ до +∞.
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1, 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A1. Определение дается через координаты точки A1(x , y).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A1(x , y). sin α=y
Косинус (cos) угла поворота
Косинус угла поворота α – это абсцисса точки A1(x , y). cos α=х
Тангенс (tg) угла поворота
Тангенс угла поворота α – это отношение ординаты точки A1(x , y) к ее абсциссе. tg α=yx
Котангенс (ctg) угла поворота
Котангенс угла поворота α – это отношение абсциссы точки A1(x , y) к ее ординате. ctg α=xy
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0, 1) и (0, -1). В таких случаях выражение для тангенса tg α=yx просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α.
Тангенс определен для всех углов, кроме α=90°+180°·k, k∈Z (α=π2+π·k, k∈Z)
Котангенс определен для всех углов, кроме α=180°·k, k∈Z (α=π·k, k∈Z)
При решении практических примеров не говорят “синус угла поворота α”. Слова “угол поворота” просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10π равен синусу угла поворота величиной 10π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами (1, 0).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t.
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t=y
Косинус (cos) числа t
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t=x
Тангенс (tg) числа t
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. tg t=yx=sin tcos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α, cos α, tg α, ctg α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A(1,0) на угол величиной до 90 градусов и проведем из полученной точки A1(x,y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A1OH равен углу поворота α, длина катета OH равна абсциссе точки A1(x,y). Длина катета, противолежащего углу, равна ординате точки A1(x,y), а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α=A1HOA1=y1=y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α, при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Синус, косинус, тангенс и котангенс: основные формулы
Источник