Какие свойства силы бывают
 Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Сила характеризует количественную сторону механического взаимодействия. Таким образом, когда говорят, что на тело действуют силы, то это значит, что на него воздействуют другие тела (или физические поля). Не всегда, впрочем, сила действительно приводит к изменению движению тела; такое изменение может блокироваться действием других сил. С учетом сказанного запишем:
Сила (ньютонова) – мера механического воздействия на некото- рое материальное тело со стороны другого материального тела (или физического поля); она характеризует интенсивность и направление этого воздействия. Это, разумеется, не определение, а лишь пояснение к понятию силы. Поскольку понятие силы – фундаментальное, то его точный смысл раскрывается в аксиомах механики.
Пока же мы отметим вот что. Оговорка “ньютонова” сделана потому, что в динамике мы встретимся с другими величинами, также именуемыми силами, которые, однако, не являются мерами механического взаимодействия. В этом же семестре речь будет идти именно о ньютоновых силах, и мы для краткости будем называть их просто силами.
Далее, под словом “мера” в механике и в физике понимается физическая величина, которая служит для количественного описания какого-либо свойства или отношения. В данном случае речь идет об описании именно механического взаимодействия (а бывают еще, как Вы знаете, и другие взаимодействия – тепло- вые, химические и прочие).
В физике элементарных частиц выделяют четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. Эти четыре взаимодействия лежат в основе всех наблюдаемых явлений – относящихся как к механике, так и к другим разделам естествознания.
Однако в макромире фундаментальные взаимодействия проявляются, как правило, опосредованно, и нам приходится иметь дело со значительно более широким перечнем взаимодействий (уже не обязательно фундаментальных). Если говорить о механических взаимодействиях, то речь может идти о силах различного происхождения.
Примеры сил: силы тяжести, силы упругости, архимедовы силы, силы сопротивления среды и др. В большинстве задач механики, впрочем, физическая природа тех или иных сил обычно интереса не представляет.
Ещe мы, поясняя понятие силы, говорили об интенсивности и направлении воздействия. Это означает, что сила является векторной величиной. Именно, это – вектор, приложенный к определeнной точке материального тела. Поэтому можно говорить о таких характеристиках силы.
Сила характеризуется:
1) величиной (модулем);
2) направлением;
3) точкой приложения.
К сожалению, на экзамене нередко приходится встречаться с полным пренебрежением к этому правилу. В лучшем случае экзаменатор в этой ситуации поступит так: вздохнет и попросит студента быстренько проставить обозначения векторов в тексте ответа на поставленный вопрос. Если студент не сумеет правильно проставить обозначения – это первый шаг на пути к получению “двойки”. Поэтому, пожалуйста, не игнорируйте в своих конспектах черту, если она написана на доске.
Круглые скобки с запятой в середине обозначают скалярное произведение векторов (запятая при этом разделяет сомножители). Обратите внимание: во многих книгах скалярное произведение обозначается иначе – точкой между век- торами, причем точку обычно можно опустить.
Но мы будем придерживаться именно таких обозначений (они тоже достаточно распространены). Помимо всего прочего, они позволяют избежать путаницы (ведь скалярное произведение векторов нужно отличать от обычного произведения двух скаляров).
Пока мы говорили только о векторе силы. Но понятие силы не сводится к понятию ее вектора. Важна еще и точка приложения силы: ведь если тот же по величине и направлению вектор силы приложить в другой точке тела, то его движение может измениться.
В геометрии принята следующая терминология. Свободный вектор (или просто вектор) – вектор, характеризуемый только модулем и направлением. Связанный вектор – вектор, характеризуемый еще и точкой приложения. Иногда используют такие обозначения.
Через u—.A обозначается связанный вектор, получаемый, если свободный вектор u— приложить в точке A. Обратите внимание: здесь точка пишется не в середине строки (как при умножении чисел), а на ее нижней линии. Таким образом, можно сделать следующий вывод. Итак, сила – связанный вектор (полное обозначение: F—-.A).
Там, где нам потребуется подчеркнуть наличие у силы определенной точки приложения, мы будем пользоваться именно этим полным обозначением. Там, где точка приложения силы будет заранее оговорена, мы будем применять сокращенное обозначение, обозначая силу просто F—- (т.е. так же, как и вектор силы). О точке приложения силы нужно сказать следующее: Если сила действует на материальную точку, то точкой приложения служит сама эта точка.
Если сила действует на материальное тело, то точкой приложения служит точка тела (она может меняться с течением времени). В общем случае точка приложения силы не может лежать вне тела. Если тело – абсолютно твердое, то данное ограничение можно снять; но об этом мы будем говорить позже.
Возникает вопрос: а как можно на практике задать точку приложения силы? Любую точку можно задать, например, ее радиус-вектором, проведенным из некоторого полюса. Полюс – произвольно выделенная точка (положение которой обычно предполагается известным).
Раз здесь говорится “обычно”, то текст в скобках Вы вполне можете игнорировать. Часто бывает так: взяли некоторую точку и объявили ее полюсом (и будет она с этого времени считаться таковым). Но для задания положения точки приложения силы нам как раз нужно знать положение полюса. Можно – но не обязательно – принять за полюс начало системы координат.
Употребляют оба обозначения, но первое предпочтительнее: вектор обозначается одной буквой, а буква “r” напоминает, что речь идет именно о радиус- векторе, или шестью скалярами (Fx , Fy , Fz , xA , yA , zA ). Это – удобно, и так поступают часто. Но задать силу можно также иным способом, который мы рассмотрим в следующем пункте.
Источник

В физике сила может быть определена как толчок или тяга на любой объект, который имеет массу. Это меняет движение объекта.
Другими словами, сила заставляет объект с массой изменить свое направление и скорость.
Два великих физика Исаак Ньютон и Галилео Галилей описали поведение сил математически. В 1638 году Галилей провел эксперимент на наклонной плоскости, который произвел революцию в способе измерения силы. Пять десятилетий спустя Ньютон разработал законы движения, которые заложили основу классической механики.
Поскольку сила имеет и величину, и направление, она является векторной величиной. Она представлена символом F и измеряется в единице СИ Ньютона (N).
Силы можно разделить на две группы в зависимости от их применения:
- Контактная сила: действует на тело напрямую или через среду.
- Бесконтактная сила: действует через пространства без прямого контакта с телом.
Чтобы лучше объяснить это явление, мы описали все различные типы сил на примерах. Давайте начнем с четырех фундаментальных сил в природе.
1. Гравитационная сила
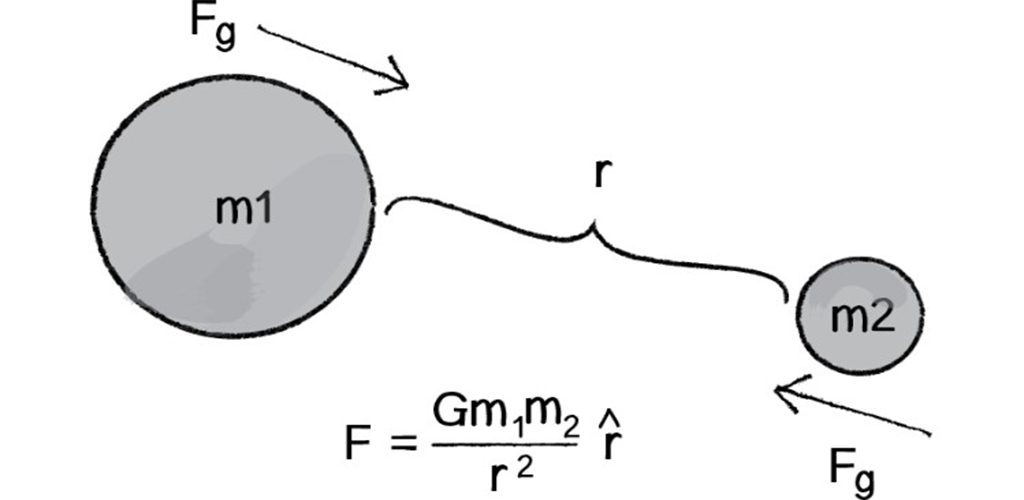
Тип: бесконтактная сила
Гравитационная сила – это то, что притягивает два объекта с массой. Она действует на каждый объект, включая вас, во Вселенной.
Величина гравитационной силы, оказываемой объектами друг на друга, “прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними”. Чем массивнее объекты и меньше расстояние между ними, тем выше сила.
Это самая слабая из четырех фундаментальных сил, обнаруженных в природе.
Хотя гравитационная сила не оказывает существенного влияния на субатомном масштабе, она является доминирующим взаимодействием на макроскопическом масштабе и существенно влияет на формирование, строение и траекторию небесных тел.
Пример: гравитация заставляет яблоко падать с дерева; она заставляет Луну вращаться вокруг Земли; она удерживает газы на Солнце.
2. Электромагнитная сила
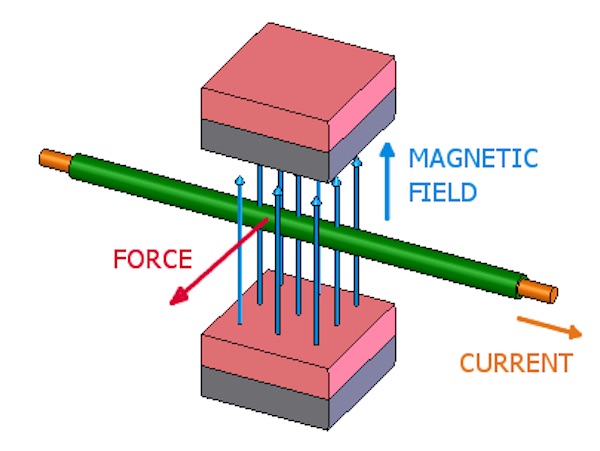
Тип: Бесконтактная сила
Это вид взаимодействия, которое происходит между электрически заряженными частицами. Электромагнитные поля (создаваемые движущимися электрическими зарядами) несут в себе электромагнитную силу.
Электричество и магнетизм связаны друг с другом: текущие электроны создают магнетизм, а движущиеся магниты генерируют электричество. Отношения между ними очень хорошо объяснены Джеймсом Клерком Максвеллом и количественно определены в его уравнениях.
Пример: Наиболее распространенным примером электромагнетизма является свет, поскольку он распространяется (излучается) в пространстве, перенося энергию электромагнитного излучения.
Следующим наиболее распространенным примером могут быть силы, действующие между электрически заряженными атомными ядрами и электронами атомов.
3. Сильная ядерная сила
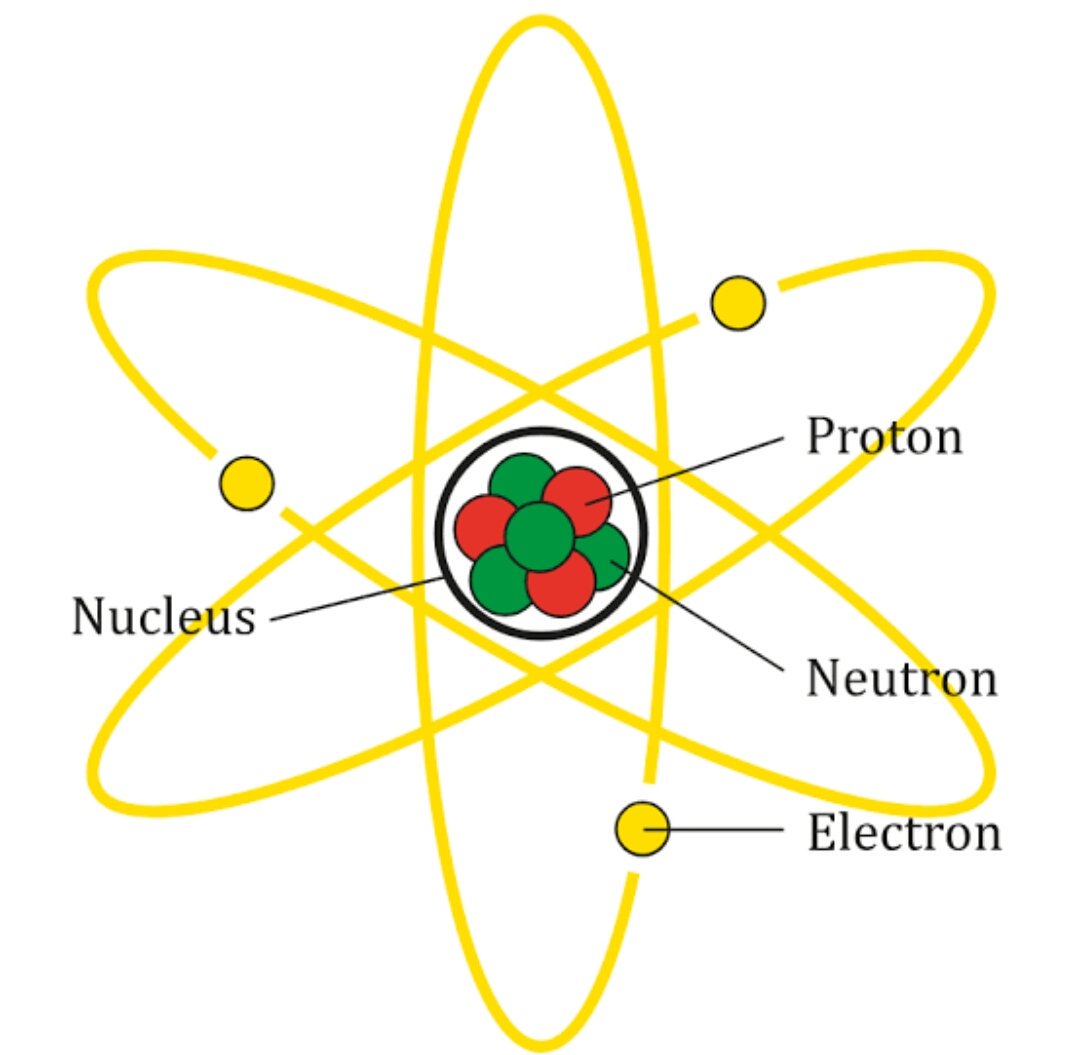
Тип: Бесконтактная сила
В ядерной физике и физике элементарных частиц сильное взаимодействие отвечает за структурную целостность атомных ядер. Поскольку все протоны имеют положительный заряд, они отталкиваются друг от друга. Сильное ядерное взаимодействие удерживает эти отталкивающие протоны вместе, так что они могут образовать атомное ядро.
Около 99% массы нейтрона или протона является результатом энергии сильного силового поля.
Это самая сильная сила в природе, действующая на расстоянии 1 фемтометра ( 10–15 м). Он почти в 137 раз сильнее электромагнетизма и в 100 миллиардов (10 38) раз сильнее, чем сила гравитации.
Пример: Сильная ядерная сила связывает кварки с адронными частицами, такими как протон и нейтрон, для создания атомного ядра. Это сила, которая соединяет обычную материю.
В более широком масштабе она используется на атомных электростанциях для производства тепла с целью выработки электроэнергии. Она также ответственна за огромную разрушительную мощь ядерного оружия. Из-за этой силы ядерное оружие при взрыве высвобождает экстремальное количество энергии.
4. Слабая ядерная сила
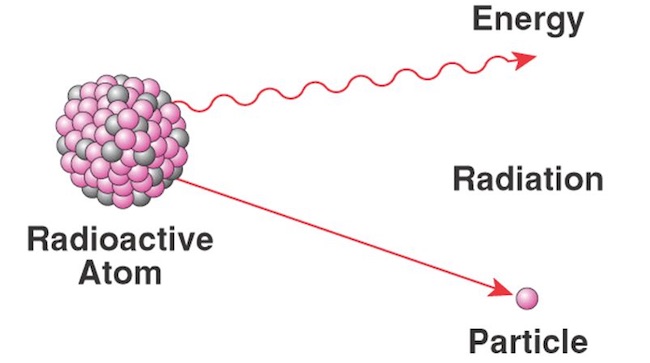
Тип: Бесконтактная сила
В ядерной физике слабое взаимодействие относится к взаимодействию между субатомными частицами, которое вызывает радиоактивный распад атомов. Более конкретно, он отвечает за распад некоторых нуклонов на лептоны и другие типы адронов.
Его напряженность поля примерно в 10 13 раз меньше, чем у сильной ядерной силы. Тем не менее, он значительно сильнее, чем гравитационная сила на коротких расстояниях.
Пример: Наиболее известным эффектом действия слабой силы является бета-распад (нейтронов) и связанная с ним радиоактивность. Она возникает в нескольких различных реакциях, включая сжигание Солнца и радиоуглеродное датирование.
Это четыре фундаментальные (бесконтактные) силы, из которых происходит все остальное. Они поддерживают горение звезд и вращение планет. Без них вселенная, которую мы знаем, не существовала бы, и даже если бы она существовала, это было бы совершенно другое место.
Теперь давайте перейдем к неосновным силам, которые возникают в результате прямого физического взаимодействия между двумя объектами.
5. Прикладная сила
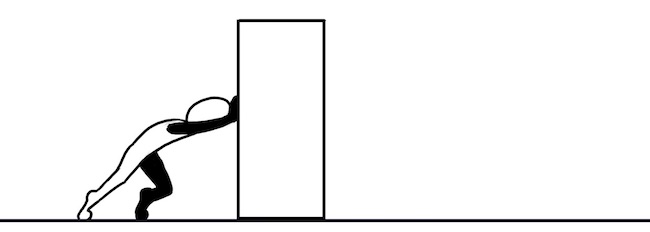
Тип: Контактная сила
Как следует из названия, это сила, которую вы применяете к объекту. Объект начинает двигаться, когда величина силы преодолевает инерцию объекта.
Тело остается в покое или в равномерном движении по прямой линии, если к ним не приложена внешняя сила, которая изменяет состояние движения и направление тела. Ускорение тела прямо пропорционально приложенной силе.
Пример: Сила, приложенная к ящику человеком.
6. Сила трения
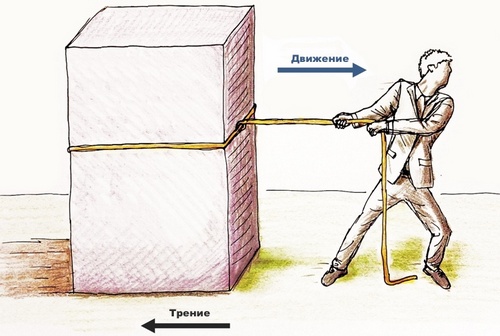
Тип: Контактная сила
Поверхностная сила, противостоящая относительному движению тела, называется силой трения. Поскольку в реальном мире ни один объект не является абсолютно гладким, всегда существует некоторое трение между двумя поверхностями. Его величина пропорциональна коэффициенту трения материала поверхности.
Двумя основными типами сил трения являются статические (сила трения о неподвижный объект) и кинетические (сила трения о движущийся объект). Сопротивление воздуха также является силой трения, которая действует на объекты, когда они перемещаются по воздуху.
Оно всегда действует в направлении, противоположном движению, и преобразует кинетическую энергию в тепловую энергию (работа в тепло). В целом, трение является критической и желательной силой, которая обеспечивает сцепление для облегчения движения по суше.
Пример: Примером трения является скольжение каботажа по столу, скольжение двух карт в колоде друг о друга и трение руки для получения тепла.
7. Нормальная сила
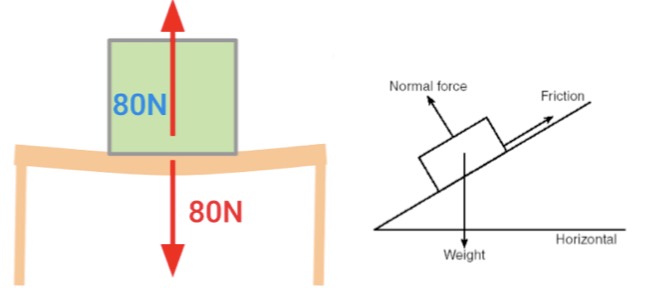
Тип: Контактная сила
Когда две поверхности находятся в контакте, они оказывают нормальное воздействие друг на друга. Термин «нормальный» относится к перпендикулярному. Это означает, что сила направлена перпендикулярно двум контактирующим поверхностям.
Пример: когда ноутбук стоит на столе, обычная сила удерживает его от падения через стол. Гравитационная сила Земли тянет ноутбук вниз, но поскольку он на самом деле не падает, должна быть сила, постоянно толкающая его вверх. Это то, что мы называем нормальной силой.
Она исходит от электромагнитной силы: электроны ноутбука толкают электроны стола. Поскольку все электроны отрицательно заряжены, они не становятся намного ближе друг к другу, и ноутбук опирается на верхнюю часть стола.
8. Сила натяжения

Сила натяжения обычно передается через провод, кабель, струну или веревку, когда она плотно натягивается силами, действующими с противоположных концов. Усилие направлено вдоль длины кабеля.
Натяжение можно также определить как действие-реакция пары сил, действующих на каждом конце кабеля. Это противоположность сжатия.
Пример: веревка, тянущая коробку или коробку, висящую на веревке, будет отличным примером натяжения (в веревке).
9. Сила упругости
Тип: Контактная сила
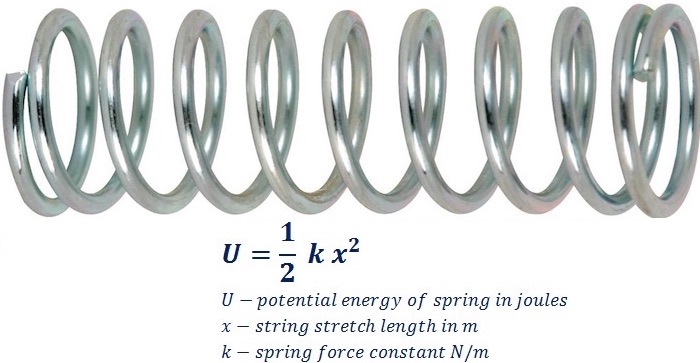
Сила упругости – это сила, прилагаемая натянутой или сжатой струной к объекту, который к ней прикреплен.
Способность пружины противостоять искажающему воздействию и возвращаться в исходное состояние при снятии воздействия зависит от ее материала, количества витков и диаметра проволоки, образующей витки. Как правило, эти характеристики количественно выражаются в параметре, называемом постоянной пружины “k”.
Для всех пружин, подчиняющихся закону Гука, величина силы прямо пропорциональна постоянной пружины (k) и сжатой/растянутой длине (x).
Пример: Автомобильные амортизаторы изготовлены из пружин. Они предназначены для поглощения ударных импульсов путем преобразования кинетической энергии удара в другую форму энергии (например, тепло), которая затем рассеивается.
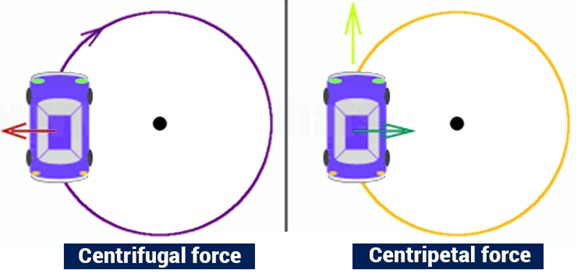
10. Центростремительная сила
Тип: Бесконтактная сила
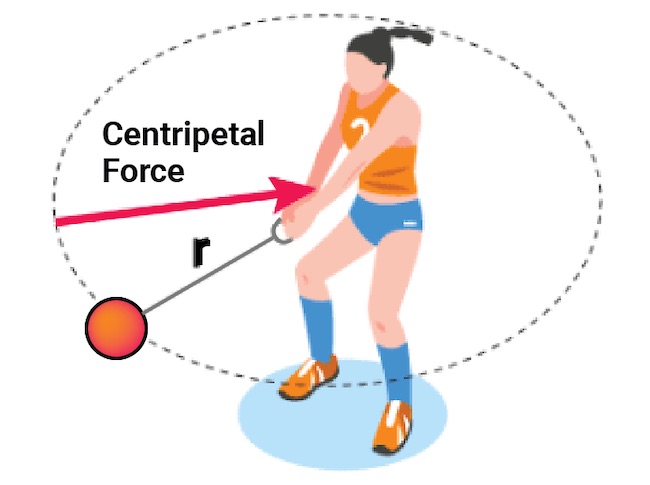
Центростремительная сила действует на объекты, ускоряющиеся в круговом движении. Это сила, которая заставляет объект следовать по изогнутому пути.
Направление этой силы всегда направлено к фиксированной точке мгновенного центра кривизны траектории и ортогонально движению объекта.
Пример: Два наиболее распространенных примера центростремительной силы – это вращение автомобиля и Земля, вращающаяся вокруг Солнца. В первом случае центростремительная сила обеспечивается за счет трения между колесами и землей, а во втором – за счет силы тяжести.
11. Сила инерции

Тип: Бесконтактная сила
Сила инерции (также называемые инерционная сила) являются очевидными силами, действующими на массы, движение которых описывается с использованием неинерциальной системы отсчета , включая вращающуюся систему отсчета.
Это вступает в силу, когда система отсчета начала ускорение. Термин «инерционная сила» имеет точное значение для ньютоновской механики – фактически он всегда пропорционален массе объекта, на который он действует.
Пример: силы, которые вы испытываете в движущемся автомобиле, являются повседневными примерами сил инерции. Когда автомобиль разгоняется в переднем направлении, он толкает вас обратно на сиденье. Когда автомобиль делает резкие повороты, он бросает вас из стороны в сторону. Эти влияния возникают из-за того, что естественная система отсчета для данной ситуации сама ускоряется.
Источник
Статика
В статике изучают свойства сил и определяют условия равновесия тел.
Свойства силы и пар сил.
Сила есть мера механического действия одного тела на другое, которая проявляется в виде деформации или изменения движения тела.
Сила есть приложенный вектор, изображаемый из точки приложения силы, определяемый двумя векторами: вектором и радиус-вектором точки её приложения.
Силу можно задавать в декартовой системе отсчета шестью скалярами: тремя проекциями силы на оси координат X, Y, Z и тремя координатами x,y,z точки приложения силы.
Силу, приложенную к абсолютно твердому телу можно считать скользящим вектором, т.е. силу можно перемещать вдоль линии её действия, минуя точку приложения, поскольку известно, что при этом механическое действие силы на тело, способность разгонять и раскручивать тело не меняются. Параллельный перенос силы не допустим – при переносе силы на параллельную линию, изменяется её вращательная способность. Силу можно раскладывать на составляющие, т.е. – заменять несколькими силами, приложенными в прежней точке тела.
Нередко, заменяют тремя составляющими:
.
Пару сил можно считать приложенной в любом месте твердого тела, момент пары есть свободный вектор, который обычно изображается из точки приложения одной из двух сил, либо – из середины плеча пары.
Внешние силы, приложенные к телу, разделяют на неизвестные силы (реакции опор, связей) и известные силы (приложенные нагрузки). В некоторых случаях известно направление реакции опоры, тогда имеем только одну неизвестную – модуль реакции опоры.
Применяется следующий прием: если в каком-либо направлении связь не препятствует бесконечно малому перемещению тела, то реакция этой связи перпендикулярна этому направлению. Система сил, приложенных к телу, называется плоской, если все неизвестные и известные силы расположены в некоторой одной плоскости 0xy.
Скалярным моментом силы относительно точки O называется произведение модуля силы и плеча силы со знаком, определяющим направление кажущегося вращения силы вокруг точки
Теорема. Если тело находится в состоянии равновесия ( не движется ), то система всех приложенных к нему внешних сил удовлетворяет трем алгебраическим уравнениям равновесия, а именно, равны нулю сумма моментов всех приложенных сил и суммы проекций сил на две оси координат :
Пример 1
| Рис.1 Рисунок к задаче |
Криволинейный стержень ОАВ, опирающийся на каток и шарнир находится в состоянии равновесия. Определить реакции связей. Задан линейные размеры, и величины сосредоточенной силы и интенсивность распределенной нагрузки , а также – момент пары приложенных сил (Рис.1)
Решение.
Освободим тело от связей, но сохраним действие связей и заменим нагрузку интенсивностью на равнодействующую , приложенную к середине участка приложения распределенной нагрузки (рис. 2). Неизвестные реакции связей направляем в положительную сторону. Продолжим пунктиром линии действия сил и покажем плечи сил относительно точки О, отметим знаком (±) направления вращения силы вместе с плечом вокруг точки О. А также перенумеруем все силы, в частности переобозначим :
| Рис.1 Реакции опор и плечи сил |
плечо силы
– плечо силы , знак (-)
– плечо , знак (+)
– плечо , знак (+), где
– плечо , знак (-)
Составим в табличной форме два уравнения проекций и уравнение моментов относительно точки :
Далее, выражая длину плеч сил через известные размеры и углы, получим систему трех линейных алгебраических уравнений относительно трех неизвестных реакций опор
Замечание: момент любой силы можно также находить и методом разложения на составляющие, что упрощает вычисление плеч сил.
Например, имеем (рис. 3)
| Рис. 3 Момент силы как сумма моментов ее проекций |
Пример 2
| Рис. 4 Рисунок к задаче |
Консольная балка, закрепленная в стене. (рис. 4), нагруженная растягивающей силой F и поперечной расперделенной нагрузкой q (например – собственным весом).
Решение
В заделке возникает реакция в виде составляющих , а так же – пара сил с неизвестным моментом удерживающие балку от вращения. Относительно О имеем плечи сил (со знаком) и уравнения равновесия в табличной форме:
В результате получаем систему уравнений вида
Отсюда окончательно получаем неизвестные реакции опоры:
Источник
