Какие свойства счетных множеств

Понятие равномощности
множеств и его свойства позволяют
выделить классы равномощных множеств.
Интересно знать, как много существует
неравномощных множеств и иметь в
некотором смысле «эталонные множества»,
чтобы, сравнивая с ними другие, было
легче устанавливать равномощность
множеств или её отсутствие.

1. Конечных,
но не равномощных множеств, бесконечно
много. Их классов столько же, сколько
натуральных чисел.

2. Бесконечных,
но не равномощных множеств, также
бесконечно много.

Возникает
вопрос: есть ли среди бесконечных
множеств множество наименьшей мощности?
Да. Это счётные множества.

Определение 1.ПустьN– множество
натуральных чисел. МножествоSназываетсясчётным
множеством,если оно равномощноN, то естьSN.

Мощность
счётного множества имеет специальное
обозначение:
(первая буква алфавита иврит, читается
«алеф-нуль»). Мы будем обозначать мощность
счётного множества буквойа:

m(S)=a.

Примеры счётных множеств

1. 2N;

2. Q;

3.
Z;

4. Множество
квадратов натуральных чисел.

Основные свойства счётных множеств

Теорема 1.Для
того чтобы множествоSбыло счётным необходимо и достаточно,
чтобы его элементы можно было занумеровать
в последовательность, члены которой
попарно различны:

.

Доказательство:

1. Необходимость.

Пусть S– счётное множество, тогда существует
биекцияf: NS.
В этой биекции образ элементаnобозначимаn,
тем самым будут занумерованы все элементы
множестваS, то есть.
Так как все элементы множестваSразличны, то и все члены последовательностипопарно различны.

2.
Достаточность.

Пусть
,аnпопарно различны. Сопоставим элементуаnего
номерn.Полученное
соответствие изSвNявляется биекцией. Следовательно, по
определениюS– счётное
множество.

Теорема
2.Во всяком бесконечном множествеА имеется счётное подмножество.

Доказательство:

Возьмём во
множестве Апроизвольный элемент.
Множество
бесконечное (доказывается от противного).
Из множества
выберем элемент.
Множество
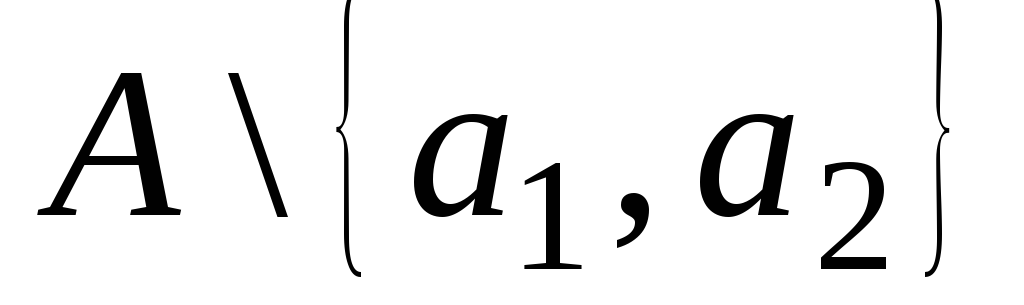– бесконечное. Из множества
выбираем элементи так далее. Так какА– бесконечное
множество, то этот процесс продолжим
до бесконечности. В результате получим
последовательность.
Так как во множествеАвсе элементы
попарно различны, по теореме 1S– счётное множество.

Следствие.
Счётная мощность является
наименьшей из мощностей бесконечных
множеств.

Доказательство:

Пусть А –
произвольное бесконечное множество.
По теореме 2 оно содержит счётное
подмножествоS, то
естьm(S)=а.
Так какS,
тоm(S)m(А)илиаm(А).

Теорема3.Всякое бесконечное подмножествоВсчётного множестваSсчётно:

ВS;
m(S)=а
m(В)=а.

Доказательство:

Так как ВS,тоm(В)m(S)=а.
Но по следствиюm(В)а.Таким образом,m(В)аиm(В)а.
По теореме Кантора-Бернштейнаm(В)=а.

Теорема 4.Бесконечное множествоВсчётно,
если существует сюрьекцияfкакого-нибудь счётного множестваSнаВ.

Доказательство:

Не умоляя
общности доказательства можно считать,
что S=N.
По условиюf: N– сюрьекция (В– это образNпри отображенииf, то
естьf(N)=В).
Возьмём любой элемент,b– образ какого-либо
натурального числа. При отображенииfего прообразом является некоторое
множество натуральных чиселf-1(b),
состоящее из тех элементов, образ которых
равенb, то естьf-1(в)={nN:
f(n)=b}.
В этом множестве существует наименьшее
натуральное число.
Рассмотрим множество– бесконечное множество (От противного:
пустьАконечно. Тогда для бесконечного
числа элементовсуществует один элементN, то есть
одному элементуnNсоответствует бесконечно много элементов.
Это означает, что соответствиеNне является отображением. Получили
противоречие с условием. Следовательно,
предположение не верно.). Так какАNиА– бесконечное множество, то по
теореме 3 множествоАсчётно.
Рассмотрим соответствие,при котором.
Это соответствие является биекцией.
Следовательно,АВиВсчётно.

Определение
2. Кортежемназывается конечное множество элементов.

Теорема
5.МножествоКвсевозможных
кортежей, составленных из натуральных
чисел, счётно.

Доказательство:

Пусть Р– множество всех простых чисел,
расположенных в порядке возрастания:

Р=(рк),
р1=2, р2=3,
р3=5,… .

Возьмём любой
кортеж из натуральных чисел (n1,n2,…,nk)и поставим в соответствие ему число

N.

Например,

.

На основании теоремы
о единственности разложения чисел на
простые множители различным кортежам
соответствуют различные натуральные
числа, то есть если

,
то.

Рассмотрим
соответствие f:KА,
гдеА– некоторое бесконечное
подмножество множестваN,
то естьА– счётно (по теореме 3).
Указанное соответствие является
биекцией. Так какАсчётно и,
тоKтакже счётно.

Определение 3.Декартовым произведением
А1А2…Аmназывается множество, состоящее из
кортежей,
где.

Теорема
6.Декартово произведение
конечного числа счётных множеств счётно.

Доказательство:

Пусть А1,А2,…,Аm– счётные множества. Докажем, чтоА1А2…Аm=А
– счётное множество. Счётные множестваАk,,представим в виде последовательностей

;

;

…………………………………

;

.

Возьмём
,
поставим ему в соответствие кортеж из
натуральных чисел.
Обозначим.
Указанное соответствие является биекциейf:А1.
Но1– бесконечное подмножество счётного
множестваиз
теоремы 5. По теореме 31счётно. Так какf–
биекция, тоА счётно.

Теорема
7. Объединение конечной или
счётной совокупности счётных множеств
счётно.

Доказательство:

Пусть
А1,А2,…,Аm,…
– счётные множества. Докажем, что– счётное множество.

1. Пусть
– объединение счётного числа счётных
множеств. Счётные множестваАmпредставим в виде последовательностей

;

;

…………………………………

;

……………………………………

,

где
– это элемент множествас номером.
Рассмотрим множествоN2=N´N. Оно счётно по теореме 6. Возьмём любой
элемент(p,q)ÎN2.
Сопоставим ему элемент.
Так как любой элементпринадлежит хотя бы одному из множествАpи имеет
в нём определённый номерq,
то указанное соответствие является
сюрьекциейf:N2®A.
Так как множествоN2счётно, то по теореме 4 множествоАсчётно.

2. Пусть
– объединение конечного числа счётных
множеств. Положим

,

тогда
.
По первой части теоремы множествоАсчётно.

Теорема
8.МножествоQрациональных чисел счётно.

Доказательство:

Представим
множество Qв виде

Q
=Q+Q–,

Q+={m/n,
m,nN,
(m,n)=1},

={m/n,
m,n},

Q+,

,

где Qn– множество дробей видас фиксируемым знаменателем.
Очевидно, чтоQn,
то естьQnсчётное множество. Тогда по теореме 7
также счётно. НоQ+является бесконечным подмножеством
счётного множества
.
Тогда по теореме 3 множествоQ+счётно. В силу того, чтоQ+~Q–,
заключаем, что множествоQ–счётно. По теореме 7 множествоQ+Q–счётно, тогда по теореме 1 множествоQсчётно.

Теорема
9.Объединение счётной совокупности
конечных множеств конечно или счётно.

Доказательство:

Пусть
– конечные множества,.

1. Множество
А может быть конечным (например,
если все множестваАkравны:N).

2. Рассмотрим
случай, когда множество А– бесконечно.
Пусть множествоАkимеетnkэлементов. Присоединим к этому множеству
все натуральные числа, большие чемnk,
получим счётное множествоВk.
Проделаем это для всехk.
Рассмотрим множество.
По теореме 7 множествоВсчётно. НоАи является
его бесконечным подмножеством. По
теореме 3 множествоАсчётно.

Теорема 10.Мощность бесконечного множества не
изменяется, если к нему присоединить
конечное или счётное множествоS.

Доказательство:

Случай
конечного множества Sне интересен, так как является следствием
теоремы 1. Рассмотрим случай счётного
множестваS. Не нарушая
общности доказательства будем считать,
что=.
По теореме 2 множествоВможно
представить в виде,
гдеS1–
счётное множество множестваS.
Тогда

.

Так как
множества
иS1– счётные
множества, то существует биекцияf:S1.Рассмотрим отображение,
определяемое следующим образом:

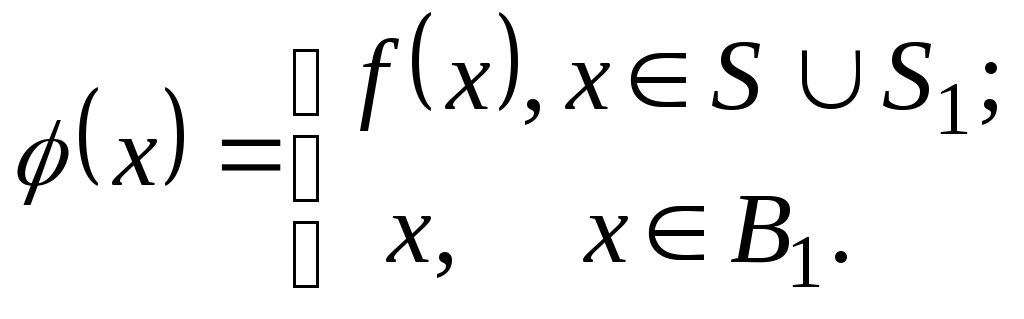
Это отображение
является биекцией
.
Следовательно,,
то есть.

Определение
4.Если бесконечное множество
не является счётным, то оно называетсянесчётным.

Теорема 11. Мощность
несчётного множестваМне изменяется,
если из него удалить конечное или счётное
подмножествоS.

Доказательство:

Пусть М– несчётное множество, тогдаМS– бесконечное множество (доказательство
от противного). Тогда по теореме 10
.

Определение 5.Числоназываетсяалгебраическим,если оно является корнем некоторого
многочлена с целыми коэффициентами.

Теорема
12. МножествоАвсех
алгебраических чисел счётно.

Доказательство:

Пусть М– множество всех многочленов с целыми
коэффициентами,Мn– множество многочленов с целыми
коэффициентами и с фиксированной
степеньюn. Возьмём
любой многочлен,,
из множестваМn.
Этому многочлену сопоставим кортеж из
его коэффициентов(аn
,…,а0). Множество таких
кортежей обозначимТ. Очевидно, чтоТ=(Z{0})Zn. Построенное
соответствие является биекциейf:МnT.
Так как множествоZсчётно, то по теореме 3 множествоZ{0}также счётно. Следовательно, по теореме
6 множествоТсчётно. Так какf– биекция, тоМn~T,
то естьМnсчётно. Так каки все множестваМnсчётны, то по теореме 7 множествоМсчётно. Итак, множество всех многочленов
с целыми коэффициентами счётно и любой
многочлен имеет конечное число корней.
Следовательно, множествоАпредставляет
собой объединение счётного числа
конечных множеств. Так какА–
бесконечное множество, то по теореме 9
оно счётно.