Какие свойства проявляет микрочастица

1923 год ознаменовался событием, значимо ускорившим развитие квантовой физики. Французским физиком Л. де Бройлем была предложена гипотеза, предполагающая универсальность корпускулярно-волнового дуализма.  В своей концепции Де Бройль сформулировал утверждение о том, что, помимо фотонов и электроны, а также прочие частицы материи имеют как корпускулярные, так и волновые свойства.

Описание гипотезы де Бройля

Идеи де Бройля содержали мысль о том, что любой микрообъект имеет, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота v и длина волны λ. При этом количественное соотношение корпускулярных и волновых характеристик аналогично тому же для фотона:

E=hv, p=hvc=hλ.

Как уже было сказано выше, в гипотезе французского физика шла речь о всех видах микрочастиц, соответственно и указанное выше соотношение применимо для любых из них, в том числе, и для обладающих массой m. Любая частица, обладающая импульсом, была сопоставлена с волновым процессом с длиной волны λ=hp.

Для частиц, имеющих массу: λ=hp=h1-v2/c2mv.

В нерелятивистском приближении (υ<<c)

λ=hmv.

Основой идей де Бройля стали размышления о симметрии свойств материи, и в то время, увы, гипотеза не получила опытного подтверждения. Однако, она стала мощнейшим катализатором развития новых идей о природе материальных объектов. На протяжении последующих нескольких лет выдающиеся умы XX века (физики В. Гейзенберг, Э. Шредингер, П. Дирак, Н. Бор и др.) создавали теоретические основы новой науки, названной квантовой механикой.

Дифракция электронов

Впервые гипотеза де Бройля была экспериментально подтверждена в 1927 году, когда американские физики К. Девиссон и Л. Джермер выяснили, что пучок электронов, рассеивающийся на кристалле никеля, дает ясную дифракционную картину, похожую на возникающую тогда, когда на кристалле рассеивается коротковолновое рентгеновское излучение. В исследованиях физиков кристалл служил естественной дифракционной решеткой. По тому, какое положение имели дифракционные максимумы, выяснилась длина волны электронного пучка, и она полностью соответствовала той, что вычислялась по формуле де Бройля.

В 1928 году физик из Англии Г. Томсон (являющийся сыном Дж. Томсона, который открыл за 30 лет до этого электрон) вновь подтвердил гипотезу де Бройля. Эксперименты Томсона позволили наблюдать дифракционную картину, которая возникала, когда пучок электронов проходил через тонкую поликристаллическую фольгу из золота.

Рисунок 5.4.1. Упрощенная схема опытов Г. Томсона по дифракции электронов. K – накаливаемый катод, A– анод, Ф – фольга из золота.

За фольгой установлена фотопластинка, на которой наблюдались явные концентрические светлые и темные кольца. Радиусы этих колец варьировались в зависимости от скорости электронов (т. е. длины волны) согласно де Бройлю (рис. 5.4.2).

Рисунок 5.4.2. Картина дифракции электронов на поликристаллическом образце при длительной экспозиции (a) и при короткой экспозиции (b).

В случае (b) видны точки попадания отдельных электронов на фотопластинку.

В последующие годы эксперимент Г. Томсона многократно повторяли и результат был неизменен даже в тех случаях, когда поток электронов был столь слабым, что через прибор единовременно проходила только одна частица (например, опыт В. А. Фабриканта в 1948 г.). Так была доказана идея, что волновые свойства характерны как для большой совокупности электронов, так и для каждого электрона в отдельности.

В последующем явления дифракции обнаружились и для нейтронов, протонов, атомных и молекулярных пучков. Доказанное экспериментально наличие волновых свойств различных видов микрочастиц позволило сделать вывод об универсальности этого явления в природе, являющегося общим свойством материи. Если продолжать данное рассуждение, волновыми свойствами должны обладать и макроскопические тела. Но из-за больших показателей массы, присущих макроскопическим телам, их волновые свойства затруднительно доказать при помощи экспериментов.

Пример 1

К примеру, пылинка массой 10–9 г, которая движется со скоростью 0,5 м/с, обладает волной де Бройля с длиной примерно 10–21 м, т. е. меньше размера атома на 11 порядков. Подобная длина волны находится за границами области, которая доступна для наблюдения.

Приведенный пример демонстрирует, что для макроскопических тел доступно лишь проявление корпускулярных свойств.

Приведем еще пример.

Пример 2

Резюмируя, еще раз отметим, что гипотеза де Бройля о корпускулярно-волновом дуализме, доказанная экспериментально, глобально поменяла представления о том, какими свойствами обладают микрообъекты.

Определение 1

Эти заключения были сформулированы датским физиком Н.Бором и получили название принципа дополнительности. Упрощенно возможно говорить о том, что микрообъекты распространяются как волны, а обмениваются энергией как частицы.

Если смотреть на вопрос с позиции волновой теории: существует соответствие максимумов в дифракционной картине электронов и максимальной интенсивности волн де Бройля. Наибольшее количество электронов находится в областях максимумов, зарегистрированных на фотопластинке. Однако схема попадания электронов в различные места на фотопластинке не индивидуальна. В принципе нет возможности заранее предположить, куда попадет очередной электрон после рассеяния; допустима только некоторая вероятность попадания электрона в то или иное место. Следовательно, описать состояние микрообъекта и его поведение возможно только, опираясь на понятие вероятности.

Факт, что необходимо использовать вероятностный подход, описывая микрообъекты, является важной отличительной чертой квантовой теории. Квантовая механика для характеристики состояний микрообъектов включает в себя понятие волновой функции Ψ (пси-функции).

Определение 2

Квадрат модуля волновой функции |Ψ|2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства.

Определенный вид волновой функции задается внешними условиями, в которых находится микрочастица. Математический инструментарий квантовой механики дает возможность определять волновую функцию частицы, которая находится в заданных силовых полях. Безграничная монохроматическая волна де Бройля является волновой функцией свободной частицы, на которую не действуют никакие силовые поля.

Максимально четко явление дифракции наблюдается тогда, когда размерность препятствия, на котором происходит дифракция волн, соизмерима с длиной волны. Подобное поведение характерно для волн любой физической природы и, в частности, электронных волн. Для волн де Бройля естественная дифракционная решетка – это упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Нет возможности создать искусственным образом препятствие указанного размера (к примеру, отверстие в непрозрачном экране), однако, чтобы уяснить природу волн де Бройля, возможно проводить, так сказать, мысленные эксперименты.

Для примера разберем дифракцию электронов на одиночной щели шириной D (рис. 5.4.3)

Рисунок 5.4.3. Дифракция электронов на щели. График справа – распределение электронов на фотопластинке.

Из общей массы электронов, проходящих через щель, свыше 85% окажутся в центральном дифракционном максимуме. Угловая полуширина θ1 этого максимума определится из условия

Dsinθ=λ

Указанная формула – часть волновой теории. Если рассуждать, опираясь на корпускулярные свойства, возможно сказать, что, когда электрон проходит через щель, он получает дополнительный импульс в перпендикулярном направлении. Можем пренебречь оставшимися 15% электронов, попадающих на фотопластинку за пределами центрального максимума, и тогда будем считать, что максимальное значение py поперечного импульса равно:

pу=p·sin θ1=hλ·sin θ1

В этой формуле p является модулем полного импульса электрона, равным (по гипотезе де Бройля) hλ. Величина p, когда электрон проходит через щель, неизменна, поскольку неизменной является длина волны λ. Указанные выражения дают возможность записать следующее соотношение:

pу=hD

Для задач квантовой механики это несложное с виду соотношение, служащее следствием волновых свойств микрочастицы, имеет глубочайший смысл. Электроны проходят через щель, что есть эксперимент, где y – координата электрона – определяется с точностью Δy = D.

Определение 3

Величина Δy носит название неопределенности измерения координаты.

Вместе с тем, точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, учитывая побочные максимумы дифракционной картины.

Определение 4

Эта величина носит название неопределенности проекции импульса и обозначается как Δpy.

Определение 5

Величины Δy и Δpy следует уяснить в том смысле, что микрочастицы не обладают одновременно точным значением координаты и соответствующей проекцией импульса. Соотношение неопределенностей не имеет отношения к несовершенству используемых приборов, чтобы одновременно измерить координаты и импульс микрочастицы. Соотношение Гейзенбурга есть проявление той самой дуальной корпускулярно-волновой природы материи микрообъектов. Соотношение дает возможность дать оценку тому, насколько применимы к микрочастицам постулаты классической механики. Оно также демонстрирует, что к микрообъектам невозможно применить понятие траектории в классическом понимании, поскольку характеристикой движения по траектории в любой момент времени являются определенные значения координат и скорости. В принципе нет возможности указать траекторию, по которой в некотором мысленном эксперименте двигался некий определенный электрон после прохождения щели до фотопластинки.

И все же определенные условия создают ситуацию, когда соотношение неопределенностей не является противоречием классическому описанию движения тел, в частности, микрочастиц.

Пример 3

Так, используя соотношение неопределенностей, есть возможность выяснять, насколько справедливы законы классической физики в отдельных случаях.

Проведем еще мысленный эксперимент: это будет дифракция электронного пучка на двух щелях
(рис. 5.4.4).

Структура эксперимента аналогична структуре оптического интерференционного опыта Юнга.

Рисунок 5.4.4. Дифракция электронов на двух щелях.

Проанализировав данный эксперимент, мы можем отметить некоторые трудности логических умозаключений в квантовой теории. Собственно, то же затруднение имеет место быть при попытке объяснить оптический опыт Юнга на основе концепции фотонов.

Если в ходе нашего эксперимента закрыть одну из щелей, мы будем наблюдать исчезновение интерференционных полос, а на фотопластинке будет зарегистрировано распределение электронов, продифрагировавших на одной щели (рис. 5.4.3), т.е. долетая до фотопластинки, электроны проходят через одну щель. Открыв обе щели, мы вновь наблюдаем интерференционные полосы, и становится закономерным вопрос: так сквозь какую из щелей проходит каждый электрон?

Конечно, довольно затруднительно представить с точки зрения присущей нашему мышлению логике, что единственным ответом на указанный выше вопрос является факт, что электрон проходит через обе щели. Нашему мышлению свойственно представлять поток микрообъектов в виде направленного движения, например, маленьких шариков и соответственно описывать это движение, опираясь на законы классической физики. Однако для всех микрочастиц характерны как корпускулярные, так и волновые свойства. Нам легко представится, как электромагнитная световая волна пройдёт сквозь две щели в оптическом эксперименте Юнга, поскольку волна не имеет локализации в пространстве. Но при рассмотрении концепции фотонов приходится принять, что и каждый фотон не имеет локализации. Мы не имеем возможности указать, через какую щель прошел фотон, как и не имеем возможности отследить точную траекторию полета фотона до фотопластинки с указанием точной точки его попадания. Опыты демонстрируют такую картину, что, даже когда фотоны проходят сквозь интерферометр поштучно, интерференционная картина после прохождения многих независимых фотонов все равно имеет место быть. Таким образом, квантовая физика формулирует вывод: фотон интерферирует сам с собой.

Сказанное выше имеет отношение и к эксперименту по дифракции электронов на двух щелях. Все известные экспериментальные факты в своей совокупности могут быть объяснены, если признать, что волна по де Бройлю каждого конкретного электрона проходит одномоментно сквозь обе щели, и, как результат, имеет место явление интерференции.

Определение 6

Поштучный поток электронов также дает интерференцию при длительной экспозиции, т. е. электрон, как и фотон, интерферирует сам с собой.

В заключение приведем иллюстрации:

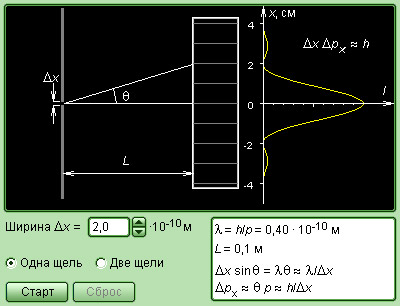
Рисунок 5.4.5. Модель волновых свойств частиц.

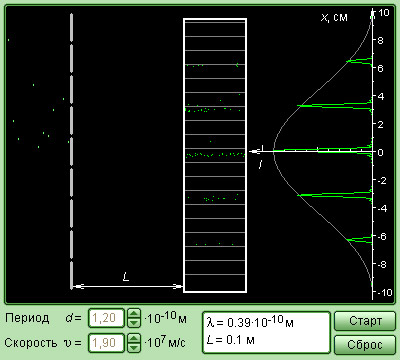
Рисунок 5.4.6. Модель дифракции электронов.