Какие свойства произведения векторов вы знаете
Определение векторного произведения
Перед тем, как дать понятие векторного произведения, обратимся к вопросу о ориентации упорядоченной тройки векторов a→, b→, c→ в трехмерном пространстве.
Отложим для начала векторы a→, b→, c→ от одной точки. Ориентация тройки a→, b→, c→ бывает правой или левой, в зависимости от направления самого вектора c→. От того, в какую сторону осуществляется кратчайший поворот от вектора a→ к b→ с конца вектора c→, будет определен вид тройкиa→, b→, c→.
Если кратчайший поворот осуществляется против часовой стрелки, то тройка векторов a→, b→, c→ называется правой, если по часовой стрелке – левой.
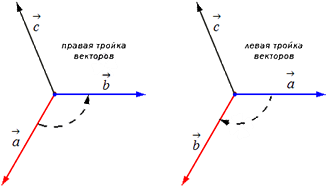
Далее возьмем два не коллинеарных вектора a→ и b→. Отложим затем от точки A векторы AB→=a→ и AC→=b→. Построим вектор AD→=c→, который одновременно перпендикулярный одновременно и AB→ и AC→. Таким образом, при построении самого вектора AD→=c→ мы можем поступить двояко, задав ему либо одно направление, либо противоположное (смотрите иллюстрацию).
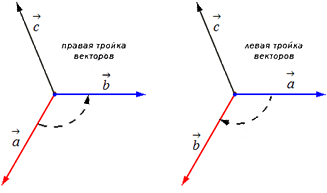
Упорядоченная тройка векторов a→, b→, c→ может быть, как мы выяснили правой или левой в зависимости от направления вектора.
Из вышесказанного можем ввести определение векторного произведения. Данное определение дается для двух векторов, определенных в прямоугольной системе координат трехмерного пространства.
Определение 1
Векторным произведением двух векторов a→ и b→ будем называть такой вектор заданный в прямоугольной системе координат трехмерного пространства такой, что:
- если векторы a→ и b→ коллинеарны, он будет нулевым;
- он будет перпендикулярен и вектору a→ и вектору b→ т.е. ∠a→c→=∠b→c→=π2 ;
- его длина определяется по формуле: c→=a→·b→·sin∠a→,b→;
- тройка векторов a→, b→, c→ имеет такую же ориентацию, что и заданная система координат.
Векторное произведение векторов a→ и b→ имеет следущее обозначение: a→×b→.
Координаты векторного произведения
Так как любой вектор имеет определенные координаты в системе координат, то можно ввести второе определение векторного произведения, которое позволит находить его координаты по заданным координатам векторов.
Определение 2
В прямоугольной системе координат трехмерного пространства векторным произведением двух векторов a→=(ax; ay; az) и b→=(bx; by; bz) называют вектор c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, где i→, j→, k→ являются координатными векторами.
Векторное произведение можно представит как определитель квадратной матрицы третьего порядка, где первая строка есть векторы орты i→, j→, k→, вторая строка содержит координаты вектора a→, а третья – координаты вектора b→ в заданной прямоугольной системе координат, данный определитель матрицы выглядит так: c→=a→×b→=i→j→k→axayazbxbybz
Разложив данный определитель по элементам первой строки, получим равенство: c→=a→×b→=i→j→k→axayazbxbybz=ayazbybz·i→-axazbxbz·j→+axaybxby·k→==a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→
Свойства векторного произведения
Известно, что векторное произведение в координатах представляется как определитель матрицы c→=a→×b→=i→j→k→axayazbxbybz, то на базе свойств определителя матрицы выводятся следующие свойства векторного произведения:
- антикоммутативность a→×b→=-b→×a→;
- дистрибутивность a(1)→+a(2)→×b=a(1)→×b→+a(2)→×b→ или a→×b(1)→+b(2)→=a→×b(1)→+a→×b(2)→;
- ассоциативность λ·a→×b→=λ·a→×b→ или a→×(λ·b→)=λ·a→×b→, где λ – произвольное действительное число.
Данные свойства имеют не сложные доказательства.
Для примера можем доказать свойство антикоммутативности векторного произведения.
Доказательство антикоммутативности
По определению a→×b→=i→j→k→axayazbxbybz и b→×a→=i→j→k→bxbybzaxayaz. А если две строчки матрицы переставить местами, то значение определителя матрицы должно меняется на противоположное,следовательно,a→×b→=i→j→k→axayazbxbybz =-i→j→k→bxbybzaxayaz=-b→×a→, что и доказывает антикоммутативность векторного произведения.
Векторное произведение – примеры и решения
В большинстве случаев встречаются три типа задач.
В задачах первого типа обычно заданы длины двух векторов и угол между ними, а нужно найти длину векторного произведения. В этом случае пользуются следующей формулойc→=a→·b→·sin∠a→,b→ .
Пример 1
Найдите длину векторного произведения векторов a→ и b→, если известноa→=3, b→=5, ∠a→,b→=π4.
Решение
С помощью определения длины векторного произведения векторов a→ и b→ решим данную задач: a→×b→=a→·b→·sin∠a→,b→=3·5·sinπ4=1522.
Ответ: 1522.
Задачи второго типа имеют связь с координатами векторов, в них векторное произведение, его длина и т.д. ищутся через известные координаты заданных векторов a→=(ax; ay; az) и b→=(bx; by; bz).
Для такого типа задач, можно решить массу вариантов заданий. Например, могут быть заданы не координаты векторов a→ и b→, а их разложения по координатным векторам вида b→=bx·i→ +by·j→+bz·k→ и c→=a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→, или векторы a→ и b→ могут быть заданы координатами точек их начала и конца.
Рассмотрим следующие примеры.
Пример 2
В прямоугольной системе координат заданы два вектора a→=(2; 1; -3), b→=(0; -1; 1). Найдите их векторное произведение.
Решение
По второму определению найдем векторное произведение двух векторов в заданных координатах:a→×b→=(ay·bz-az·by)·i→+(az·bx-ax·bz)·j→+(ax·by-ay·bx)·k→==(1·1-(-3)·(-1))·i→+((-3)·0-2·1)·j→+(2·(-1)-1·0)·k→==-2i→-2j→-2k→.
Если записать векторное произведение через определитель матрицы, то решение данного примера выглядит следующим образом: a→×b→=i→j→k→axayazbxbybz=i→j→k→21-30-11=-2i→-2j→-2k→.
Ответ: a→×b→=-2i→-2j→-2k→.
Пример 3
Найдите длину векторного произведения векторов i→-j→ и i→+j→+k→, где i→, j→, k→ – орты прямоугольной декартовой системы координат.
Решение
Для начала найдем координаты заданного векторного произведения i→-j→×i→+j→+k→ в данной прямоугольной системе координат.
Известно, что векторы i→-j→ и i→+j→+k→ имеют координаты (1; -1; 0) и (1; 1; 1) соответственно. Найдем длину векторного произведения при помощи определителя матрицы, тогда имеем i→-j→×i→+j→+k→=i→j→k→1-10111=-i→-j→+2k→.
Следовательно, векторное произведение i→-j→×i→+j→+k→ имеет координаты (-1; -1; 2) в заданной системе координат.
Длину векторного произведения найдем по формуле (см. в разделе нахождение длины вектора): i→-j→×i→+j→+k→=-12+-12+22=6.
Ответ: i→-j→×i→+j→+k→=6..
Пример 4
В прямоугольной декартовой системе координат заданы координаты трех точек A(1,0,1), B(0,2,3), C(1,4,2) . Найдите какой-нибудь вектор, перпендикулярный AB→ и AC→ одновременно.
Решение
Векторы AB→ и AC→ имеют следующие координаты (-1; 2; 2) и (0; 4; 1) соответственно. Найдя векторное произведение векторов AB→ и AC→, очевидно, что оно является перпендикулярным вектором по определению и к AB→ и к AC→, то есть, является решением нашей задачи. Найдем его AB→×AC→=i→j→k→-122041=-6i→+j→-4k→.
Ответ: -6i→+j→-4k→. – один из перпендикулярных векторов.
Задачи третьего типа ориентированы на использование свойств векторного произведения векторов. После применения которых, будем получать решение заданной задачи.
Пример 5
Векторы a→ и b→ перпендикулярны и их длины равны соответственно 3 и 4. Найдите длину векторного произведения 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→.
Решение
По свойству дистрибутивности векторного произведения мы можем записать 3·a→-b→×a→-2·b→=3·a→×a→-2·b→+-b→×a→-2·b→==3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→
По свойству ассоциативности вынесем числовые коэффициенты за знак векторных произведений в последнем выражении: 3·a→×a→+3·a→×-2·b→+-b→×a→+-b→×-2·b→==3·a→×a→+3·(-2)·a→×b→+(-1)·b→×a→+(-1)·(-2)·b→×b→==3·a→×a→-6·a→×b→-b→×a→+2·b→×b→
Векторные произведения a→×a→ и b→×b→ равны 0, так как a→×a→=a→·a→·sin0=0 и b→×b→=b→·b→·sin0=0, тогда 3·a→×a→-6·a→×b→-b→×a→+2·b→×b→=-6·a→×b→-b→×a→..
Из антикоммутативности векторного произведения следует -6·a→×b→-b→×a→=-6·a→×b→-(-1)·a→×b→=-5·a→×b→..
Воспользовавшись свойствами векторного произведения, получаем равенство 3·a→-b→×a→-2·b→==-5·a→×b→.
По условию векторы a→ и b→ перпендикулярны, то есть угол между ними равен π2. Теперь остается лишь подставить найденные значения в соответствующие формулы: 3·a→-b→×a→-2·b→=-5·a→×b→==5·a→×b→=5·a→·b→·sin(a→,b→)=5·3·4·sinπ2=60.
Ответ: 3·a→-b→×a→-2·b→=60.
Геометрический смысл векторного произведения
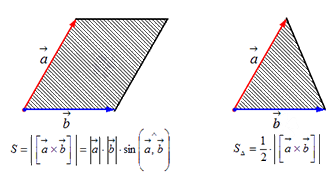
Длина векторного произведения векторов по орпеделению равна a→×b→=a→·b→·sin∠a→,b→. Так как уже известно (из школьного курса), что площадь треугольника равна половине произведения длин двух его сторон умноженное на синус угла между данными сторонами. Следовательно, длина векторного произведения равна площади параллелограмма – удвоенного треугольника, а именно произведению сторон в виде векторов a→ и b→, отложенные от одной точки, на синус угла между ними sin∠a→,b→.
Это и есть геометрический смысл векторного произведения.

Физический смысл векторного произведения
В механике, одном из разделов физики, благодаря векторному произведению можно определить момент силы относительно точки пространства.
Определение 3
Под моментом силы F→, приложенной к точке B, относительно точки A будем понимать следующее векторное произведение AB→×F→.
Источник
Прежде чем приступить к тематике статьи, напомним основные понятия.
Определение 1
Вектор – отрезок прямой, характеризующийся численным значением и направлением. Вектор обозначается строчной латинской буквой со стрелкой сверху. При наличии конкретных точек границ обозначение вектора выглядит как две прописные латинские буквы (маркирующие границы вектора) также со стрелкой сверху.
Определение 2
Нулевой вектор – любая точка плоскости, обозначается как нуль со стрелкой сверху.
Определение 3
Длина вектора – величина, равная или большая нуля, определяющая длину отрезка, составляющего вектор.
Определение 4
Коллинеарные векторы – лежащие на одной прямой или на параллельных прямых. Не выполняющие это условие векторы называют неколлинеарными.
Сложение двух векторов
Определение 5
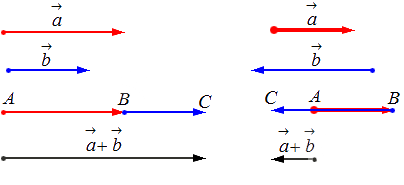
Исходные данные: векторы a→ и b→ . Для выполнения над ними операции сложения необходимо из произвольной точки отложить вектор AB→, равный вектору а→; из полученной точки undefined – вектор ВС→, равный вектору b→. Соединив точки undefined и C, получаем отрезок (вектор) АС→, который и будет являться суммой исходных данных. Иначе описанную схему сложения векторов называют правилом треугольника.
Геометрически сложение векторов выглядит так:
– для неколлинеарных векторов:
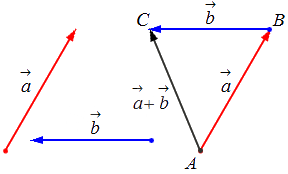
– для коллинеарных (сонаправленных или противоположнонаправленных) векторов:
Сложение нескольких векторов
Взяв за основу описанную выше схему, мы получаем возможность произвести операцию сложения векторов в количестве более 2: поочередно прибавляя каждый последующий вектор.
Определение 6
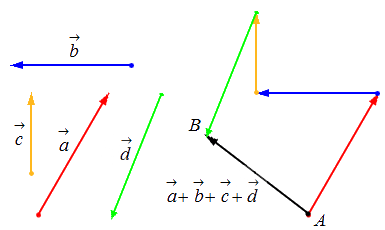
Исходные данные: векторы a→ , b→, c→,d→. Из произвольной точки А на плоскости необходимо отложить отрезок (вектор), равный вектору a→; затем от конца полученного вектора откладывается вектор, равный вектору b→; далее – по тому же принципу откладываются последующие векторы. Конечной точкой последнего отложенного вектора будет точка B, а полученный отрезок (вектор) AB→ – суммой всех исходных данных. Описанную схему сложения нескольких векторов называют также правилом многоугольника .
Геометрически оно выглядит следующим образом:
Определение 7
Отдельной схемы действия по вычитанию векторов нет, т.к. по сути разность векторов a→и b→есть сумма векторов a→ и – b→.
Умножение вектора на число
Определение 8
Чтобы произвести действие умножения вектора на некое число k, необходимо учитывать следующие правила:
– еслиk>1, то это число приведет к растяжению вектора в k раз;
– если 0<k<1, то это число приведет к сжатию вектора в 1k раз;
– если k<0, то это число приведет к смене направления вектора при одновременном выполнении одного из первых двух правил;
– если k=1, то вектор остается прежним;
– если одно из множителей – нулевой вектор или число, равное нулю, результатом умножения будет нулевой вектор.
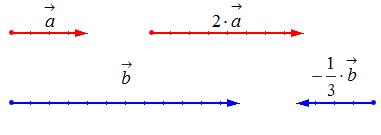
Исходные данные:
1) вектор a→и число k=2;
2) вектор b→и число k=-13.
Геометрически результат умножения в соответствии с указанными выше правилами будет выглядеть следующим образом:
Свойства операций над векторами
Описанным выше операциям над векторами присущи свойства, некоторые из которых очевидны, а прочие можно обосновать геометрически.
Исходные данные: векторы a→, b→, c→и произвольные действительные числа λ и μ.
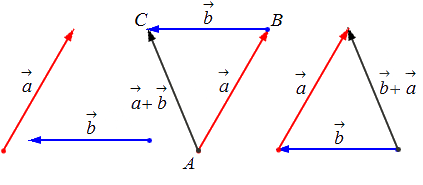
- Свойство коммутативности: a⇀+b→=b→+a→ .
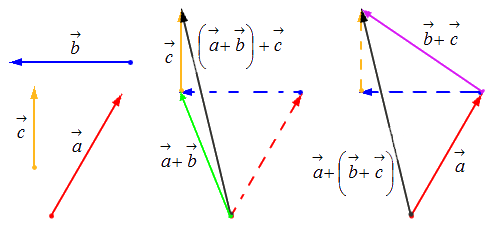
- Свойство ассоциативности: (a→+b→)+c→=a→+(b→+c→) .
- Свойство использования нейтрального элемента по сложению (нулевой вектор 0→ ⃗). Это очевидное свойство: a→+0→=a→
- Свойство использования нейтрального элемента по умножению (число, равное единице): 1·a→=a→. Это очевидное свойство, не предполагающее никаких геометрических преобразований.
- Любой ненулевой вектор a→ имеет противоположный вектор -a→ и верным является равенство: a→+(-a→)=0→. Указанное свойство – очевидное.
- Сочетательное свойство операции умножения: ( λ · µ ) · a→ = λ · ( µ·a→ ). Например, растяжение вектора при умножении на число 10 можно произвести, сначала растянув вектор в 2 раза, а затем полученный результат еще в 5 раз. Также возможен вариант умножения на число 10 при сжатии вектора в 5 раз и последующего растяжения полученного результата в 50 раз.
- Первое распределительное свойство (очевидно): ( λ + µ ) · a→ = λ ·a→ + µ · a→.
- Второе распределительное свойство: λ · (a→ +b→) = λ ·a→ + λ · b→ .
Геометрически это свойство определяется подобием треугольников: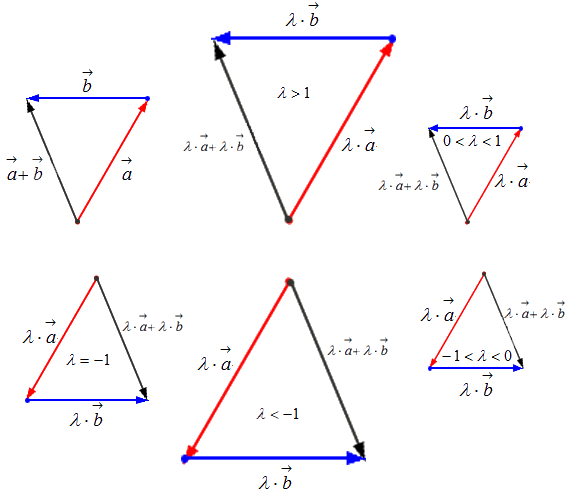
Свойства коммутативности и ассоциативности дают возможность складывать векторы в произвольном порядке.
Перечисленные свойства операций позволяют осуществлять необходимые преобразования векторно-числовых выражений аналогично привычным числовым. Рассмотрим это на примере.
Пример 1
Задача: упростить выражение a→-2·(b→+3·a→)
Решение
– используя второе распределительное свойство, получим: a→-2·(b→+3·a→)=a→-2·b→-2·(3·a→)
– задействуем сочетательное свойство умножения, выражение приобретет следующий вид: a→-2·b→-2·(3·a→)=a→-2·b→-(2·3)·a→=a→-2·b→-6·a→
– используя свойство коммутативности, меняем местами слагаемые:a→-2·b→-6·a→=a→-6·a→-2·b→
– затем по первому распределительному свойству получаем:a→-6·a→-2·b→=(1-6)·a→-2·b→=-5·a→-2·b→Краткая запись решения будет выглядеть так:a→-2·(b→+3·a→)=a→-2·b→-2·3·a→=5·a→-2·b→
Ответ: a→-2·(b→+3·a→)=-5·a→-2·b→
Источник
В данной теме мы подытожим раздел векторы, опишем все действия, которые
можно совершать над векторами и какими свойствами они обладают.
Действия над векторами
Определение
Вектором называется направленный отрезок $overline{A B}$ ,
где точка $A$ – начало, точка
$B$ – конец вектора.
Суммой $overline{a}+overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называют такой третий вектор
$overline{c}$, начало которого совпадает с началом
$overline{a}$, а конец – с концом
$overline{b}$ при условии, что конец вектора
$overline{a}$ и начало вектора
$overline{b}$ совпадают.
Свойства операции сложения:
1° $overline{a}+overline{b}=overline{b}+overline{a}$ – коммутативность
2° $(overline{a}+overline{b})+overline{c}=overline{a}+(overline{b}+overline{c})$ – ассоциативность
3° $overline{a}+overline{0}=overline{a}$
4° $overline{a}+(-overline{a})=overline{0}$
Определение
Разностью $overline{a}-overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называется вектор $overline{c}$
такой, что выполняется условие: $overline{b}+overline{c}=overline{a}$.
Произведением $alpha overline{a}$ вектора
$overline{a}$ на число
$alpha$ называется вектор
$overline{b}$, удовлетворяющий условиям:
- $overline{b} | overline{a}$
- $|overline{b}|=|alpha||overline{a}|$
- $overline{a} uparrow uparrow overline{b}$, если
$alpha>0$,
$overline{a} uparrow downarrow overline{b}$, если
$alpha
Свойства умножения вектора на число:
1° $(alpha pm beta) overline{a}=alpha overline{a} pm beta overline{a}$
2° $alpha(overline{a} pm overline{b})=alpha overline{a} pm alpha overline{b}$
3° $alpha(beta overline{a})=(alpha beta) overline{a}=beta(alpha overline{a})$
4° $1 cdot overline{a}=overline{a}$
5° $-1 cdot overline{a}=-overline{a}$
6° $0 cdot overline{a}=overline{0}$
Определение
Скалярным произведением двух ненулевых векторов $overline{a}$ и
$overline{b}$ называется число, равное произведению
длин этих векторов на косинус угла между ними:
$$bar{a} bar{b}=bar{a} cdot bar{b}=(bar{a}, bar{b})=|bar{a}||bar{b}| cos (bar{a}, bar{b})$$
Свойства скалярного произведения:
1° $(overline{a}, overline{b})=(overline{b}, overline{a})$ – симметричность.
2° $(overline{a}, overline{a})=|overline{a}|^{2}$. Обозначается
$(overline{a}, overline{a})=overline{a}^{2}$ и называется скалярный квадрат.
3° Если $overline{a} neq overline{0}$, то $(bar{a}, bar{b})=|bar{a}| cdot Пр_{bar{a}} bar{b}$
4° Если $overline{a} neq overline{0}$ и $overline{b} neq overline{0}$ и
$(overline{a}, overline{b})=0$, то $overline{a} perp overline{b}$. Верно и обратное утверждение.
5° $(overline{a}+overline{b}, overline{c})=(overline{a}, overline{c})+(overline{b}, overline{c})$
6° $(lambda overline{a}, overline{b})=lambda(overline{a}, overline{b})$
7° $(alpha overline{a}+beta overline{b}, gamma overline{c}+delta overline{d})=alpha gamma(overline{a}, overline{c})+alpha delta(overline{a}, overline{d})+beta gamma(overline{b}, overline{c})+beta delta(overline{b}, overline{d})$
Определение
Векторным произведением ненулевых векторов $overline{a}$ и
$overline{b}$ называется вектор $overline{c}$,
обозначаемый символом $[overline{a}, overline{b}]$ или
$overline{a} times overline{b}$, длина которого
|bar{c}|=|bar{a}||bar{b}| sin (bar{a}, bar{b}).
Свойства векторного произведения:
1° $[overline{a}, overline{b}]=overline{0}$, тогда и только тогда, когда
$overline{a} | overline{b}$
2° $[overline{a}, overline{b}]=-[overline{b}, overline{a}]$
3° Модуль векторного произведения $|[overline{a}, overline{b}]|$
равен площади параллелограмма, построенного на заданных векторах $overline{a}$ и
$overline{b}$ (рис. 2), т.е.
$$S=|[bar{a}, bar{b}]|=|bar{a}||bar{b}| sin (bar{a}, bar{b})$$
4° $[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]$
5° $left[overline{a}_{1}+overline{a}_{2}, overline{b}right]=left[overline{a}_{1}, overline{b}right]+left[overline{a}_{2}, overline{b}right] ;left[overline{a}, overline{b}_{1}+overline{b}_{2}right]=left[overline{a}, overline{b}_{1}right]+left[overline{a}, overline{b}_{2}right]$
Определение
Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$
Свойства смешанного произведения:
1° $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$
2° $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$
3° Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$
4° Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c})
5° $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$
6° $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$
7° $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$
8° $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$
9° $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$
10° Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$
Читать дальше: примеры решения задач с векторами.
Вы поняли, как решать? Нет?
Источник
