Какие свойства параллельных прямых включены в их определение и аксиому

Сначала рассмотрим разницу между понятиями признак, свойство и аксиома.
Определение 1
Признаком называют некий факт, по которому можно определить истинность суждения об интересующем объекте.
Пример 1
Прямые являются параллельными, если их секущая образует равные накрест лежащие углы.
Определение 2
Свойство формулируется в том случае, когда есть уверенность в справедливости суждения.
Пример 2
При параллельных прямых их секущая образует равные накрест лежащие углы.
Определение 3
Аксиомой называют такое утверждение, которое не требует доказательства и принимается как истина без него.
Каждая наука имеет аксиомы, на которых строятся последующие суждения и их доказательства.
Аксиома параллельных прямых
Иногда аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Теорема 1
Через точку, которая не лежит на заданной прямой, на плоскости можно провести лишь одну прямую, которая будет параллельной заданной.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Аксиома доказательства не требует.
Свойства параллельных прямых
Теорема 2
Свойство1. Свойство транзитивности параллельности прямых:
Когда одна из двух параллельных прямых является параллельной третьей, то и вторая прямая будет ей параллельна.
Свойства требуют доказательств.
Доказательство:
Пусть имеются две параллельные прямые $a$ и $b$. Прямая $с$ параллельна прямой $а$. Проверим, будет ли в таком случае прямая $с$ параллельна и прямой $b$.
Для доказательства будем пользоваться противоположным суждением:
Представим, что возможен такой вариант, при котором прямая $c$ параллельна одной из прямых, например, прямой $a$, а другую – прямую $b$ – пересекает в некоторой точке $K$.
Получаем противоречие согласно аксиоме параллельных прямых. Получается ситуация, при которой в одной точке пересекаются две прямые, к тому же параллельные одной и той же прямой $a$. Такая ситуация невозможна, следовательно, прямые $b$ и $c$ пересекаться не могут.
Таким образом, доказано, что если одна из двух параллельных прямых является параллельной третьей прямой, то и вторая прямая параллельна третьей прямой.
Теорема 3
Свойство 2.
Если одна из двух параллельных прямых пересекается третьей, то ею будет пересекаться и вторая прямая.
Доказательство:
Пусть имеются две параллельные прямые $а$ и $b$. Также пусть имеется некоторая прямая $с$, которая пересекает одну из параллельных прямых, например, прямую $а$. Необходимо показать, что прямая $с$ пересекает и вторую прямую – прямую $b$.
Построим доказательство методом от противного.
Представим, что прямая $с$ не пересекает прямую $b$. Тогда через точку $К$ проходят две прямые $а$ и $с$, которые не пересекают прямую $b$, т. е. являются параллельными ей. Но такая ситуация противоречит аксиоме параллельных прямых. Значит, предположение было неверным и прямая $с$ пересечет прямую $b$.
Теорема доказана.
Свойства углов, которые образуют две параллельные прямые и секущая:
накрест лежащие углы равны,
соответственные углы равны,
* сумма односторонних углов равна $180^{circ}$.
Пример 3
Даны две параллельные прямые и третья прямая, перпендикулярная одно из них. Доказать, что эта прямая перпендикулярна и другой из параллельных прямых.
Доказательство.
Пусть имеем прямые $а parallel b$ и $с perp а$.
Поскольку прямая $с$ пересекает прямую $а$, то согласно свойству параллельных прямых она будет пересекать и прямую $b$.
Секущая $с$, пересекая параллельные прямые $а$ и $b$, образует с ними равные внутренние накрест лежащие углы.
Т.к. $с perp а$, то углы будут по $90^{circ}$.
Следовательно, $с perp b$.
Доказательство завершено.
Источник
Геометрия
7 класс
Урок № 20
Аксиома параллельных прямых
Перечень рассматриваемых вопросов:
- Аксиомы и теоремы.
- Исторические сведения об аксиоматическом построении евклидовой геометрии.
- Параллельные и перпендикулярные прямые.
- Признаки параллельности прямых.
- Решение задач на доказательство параллельности прямых.
Тезаурус:
Аксиома – это утверждение, которое принимается в качестве исходного, без доказательства в рамках данной теории.
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые, параллельны третьей прямой, то они параллельны.
Основная литература:
- Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения
Построение геометрии
Геометрия на плоскости изучает фигуры: сначала даются их определения, затем доказываются свойства или отношения в виде теорем.
Однако есть утверждения, которые принимаются в качестве исходных, они не доказываются. Это аксиомы.
Аксиома – происходит от греческого «аксиос», что означает «ценный, достойный». Изначально имело смысл «самоочевидная истина».
Теорема – греческое слово, означает «зрелище, представление». В математике греков употреблялось в смысле «истина, доступная созерцанию».
Аксиома параллельных прямых.
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Следствия из аксиомы.
Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Если две прямые параллельны третьей прямой, то они параллельны.
Впервые аксиоматический подход к изложению геометрии был изложен в знаменитом сочинении Евклида «Начала» в III веке до нашей эры. Геометрию, которую мы изучаем, по сей день, называют евклидовой. Схема изучения геометрии представлена так: задаются начальные понятия (точка, прямая, плоскость), определения фигур (отрезок, луч, треугольник и др.). Затем изучаются свойства или отношения между ними в виде аксиом или теорем.
Приведём примеры аксиом, которые уже встречали в предыдущих параграфах, хотя они не назывались аксиомами.
- Через любые две точки проходит прямая, и притом только одна.
- На любом луче от его начала можно отложить отрезок, равный данному, и притом только один.
- От любого луча можно отложить угол, равный данному неразвёрнутому углу, и притом только один.
Евклид является автором аксиоматического подхода к построению геометрии.

Аксиома параллельных прямых:
через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
На рисунке через точку М проведены две прямые. Но только одна из нихпрямая b параллельна прямой а.

Утверждения, которые выводятся из аксиом или теорем, называются следствиями, и они доказываются.
Следствия из аксиомы параллельных прямых.
1. Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
Доказательство методом от противного.
Пусть a ║b, c пересекает прямую a в точке M. Предположим, что прямая c не пересекает b. Тогда через точку M проходит две прямые a и c параллельные b. Это противоречит аксиоме, значит предположение неверно, т. е. прямая c пересекает b.

2. Если две прямые параллельны третьей прямой, то они параллельны.
Доказательство методом от противного.
Пусть a ║ c, b ║ c.
Предположим, что прямые a и b не параллельны, т. е. пересекаются в точке M. Тогда через точку M проходит две прямые a и b параллельные c. Это противоречит аксиоме, значит, предположение неверно, т. е. прямая a параллельна прямой b.

Разбор заданий тренировочного модуля
№ 1. Доказать существование прямой, параллельной данной.

Объяснение:
Доказательство:
- Проведём через точку М прямую c ┴ а.
- Затем проведём прямую b ┴ c.
- Так как прямые a и b перпендикулярныпрямой c, то они параллельны.
№ 2. Через точку А, не лежащую на прямой р, проведены четыре различные прямые.
Сколько из них пересекает прямую р?

Объяснение.
1 случай. Если одна из прямых параллельна р. Тогда три других пересекают прямую р, согласно следствию 1 из аксиомы параллельных прямых.
2 случай. Если ни одна из прямых не параллельна р. Тогда все четыре пересекают прямую р.
Ответ: 3 или 4.
Источник
Аксиома параллельных прямых это один из постулатов Евклидовой геометрии, на которой построено доказательство всех современных теорем стереометрии. Это определение не только математическое, но и историческое. Именно о формулировке, истории появления и интересном признаке, который следует из этих утверждений и пойдет речь сегодня.

Немного истории
Почти все современные источники приписывают формулировку аксиомы Евклиду, но на самом деле родоначальник геометрии сформулировал немного другую аксиому, а вернее даже не аксиому, а скорее признак. Что интересно, его долгое время пытались опровергнуть, но сегодня перестали.
Пятый постулат или аксиома Евклида звучит так: Если при пересечении двух прямых третьей, сумма односторонних углов менее 180 градусов, то такие прямые пересекаются, при том с той стороны, где сумма углов меньше 180.
Ничего не напоминает? Конечно же, это третий признак параллельности прямых, вывернутый наизнанку: две прямые параллельны, если односторонние углы в сумме дают 180 градусов.
А современная трактовка аксиомы: Через точку в плоскости может быть проведена только и только одна прямая параллельная данной – принадлежит другому древнегреческому математику – Проклу. Вот такая небольшая историческая ошибка.
Формулировка
Но кто бы там ни был автором аксиомы, в любой задаче и при любом доказательстве, нужно иметь в виду: утверждение зовется аксиомой параллельных прямых и формулируется так: через точку на плоскости можно провести только одну прямую параллельную данной.
Следствия
Эта аксиома имеет два следствия, которые еще зовут свойствами параллельных прямых.
На самом деле, следствия 3, но третье в своем доказательстве имеет не только аксиому, а поэтому следствием в полной мере считаться не может. Формулируется третье следствие так: Если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Мы докажем это утверждение чуть позже.
Первое следствие из аксиомы параллельных прямых звучит так: если прямая параллельна одной из параллельных прямых, то она параллельна и третьей.
Рис. 1. Иллюстрация следствия.
Второе следствие: Если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.

Рис. 2. Иллюстрация следствия.
Оба следствия доказываются методом от противного.
Задача
Третье следствие всегда доказывается учениками как задача. Итак, необходимо доказать, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй.
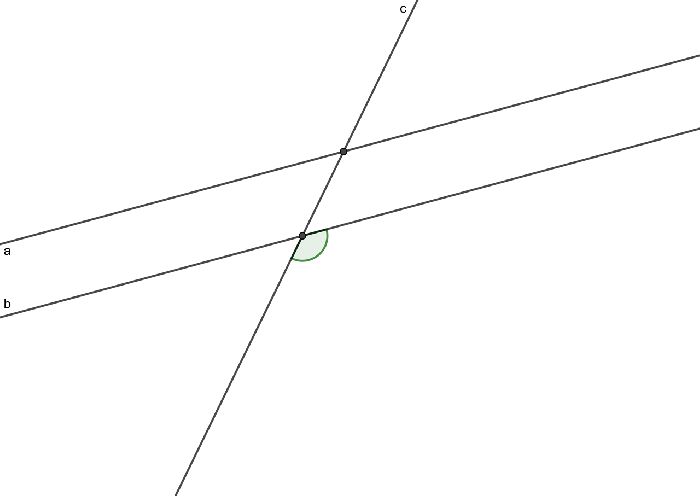
Рис. 3. Рисунок к задаче.
Проведем две параллельные прямые а и b. Прямая с перпендикулярна прямой а. Это значит, что прямая с пересекает прямую а, то есть по следствия 2 из аксиомы о параллельности прямых, прямая с пересечет и прямую b, так как b и а параллельны.
Обратим внимание на углы 1 и 2 – они являются односторонними при параллельных прямых а и b, и секущей с. Значит, сумма этих углов должна равняться 180 по свойству параллельных прямых. Но угол 1 известен, так как а перпендикулярна с, то угол равен 90 по определению перпендикулярности.
Найдем угол 2.
$$<1+<2=180$$
$$<1=90$$
$$<2=180-<1$$
$$<2=180-90=90$$
Значит, прямая с перпендикулярна прямой b по определению перпендикулярности.
Этим следствием можно пользоваться так же, как и остальными, но и забывать о том, что оно не является следствием в полном смысле этого слова не нужно.
Что мы узнали?
Мы поговорили об истории появления формулировки аксиомы параллельных прямых, узнали автора аксиомы и привели три следствия из нее, доказав третье.
Тест по теме
Оценка статьи
Средняя оценка: 4.2. Всего получено оценок: 66.
Источник
Свойства параллельных прямых крайне часто встречаются при решении задач и доказательствах теорем. Произвольные прямые – редкость, но есть такие фигуры, как квадрат или параллелограмм, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.

Что такое свойства параллельных прямых
Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.
Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются
Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.
При пересечении двух прямых секущей, образуются накрест лежащие, соответственные и односторонние углы.
Существует аксиома параллельных прямых, которая крайне важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.
Две группы свойств параллельных прямых
Свойств у параллельных прямых всего 5, но они делятся на две большие группы: следствия из аксиомы параллельных прямых и следствия из признаков параллельности прямых. Начнем с первой группы.
Следствия из параллельности прямых
Следствие 1
Если одна из двух параллельных прямых, параллельна третьей, то и другая прямая ей параллельна.
Кажется, что это логично и не требует доказательства. Но в геометрии количество утверждений не требующих обоснования крайне мало и каждое из них носит название аксиомы.
Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.
Проведем две параллельные прямые а и b. Прямая с параллельная прямой а. Предположим, что при этом с не параллельна прямой b. Тогда у нее должна быть какая-то точка пересечения К. То есть через точку К проходит две прямые с и b. При этом каждая из этих прямых должна быть параллельна прямой а.
То есть, через одну точку на плоскости проведены две прямые, параллельные данной. Это невозможно, потому что противоречит аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямые с и b параллельны.
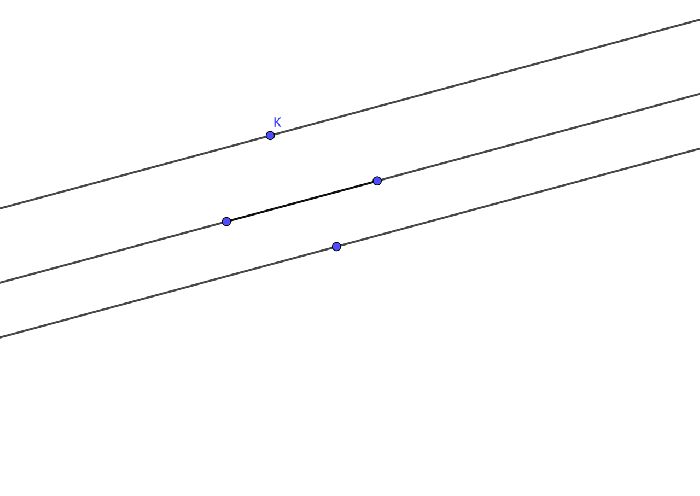
Рис. 1. Иллюстрация следствия.
Следствие 2
Следствие 2 очень важно, так как говорит о секущей двух параллельных прямых. Свойство гласит: если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
Доказательство также ведется методом от противного. Проведем две прямые: а и b. Представим, что прямая с пересекает прямую а, но не пересекает прямую b. Тогда прямые c и b параллельны. При этом с пересекает а, то есть у этих прямых есть общая точка К.
Тогда через точку к проходит прямая а и прямая с, но каждая из них параллельна b. Значит, через одну точку проходит две прямых параллельных прямой b, а это невозможно по аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямая с пересекает каждую из прямых а и b, что и требовалось доказать.
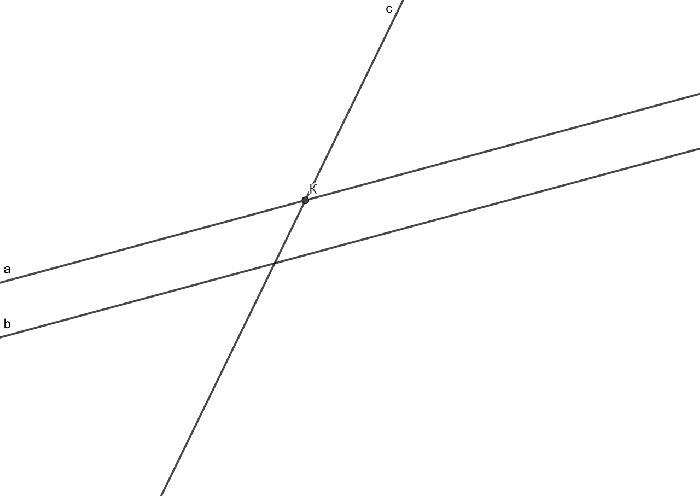
Рис. 2. Рисунок к доказательству.
Следствия из признаков параллельности
Эту группу запомнить проще всего. Свойств параллельности прямых всего 3 и каждому из них соответствует свое следствие.
- Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
- Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180
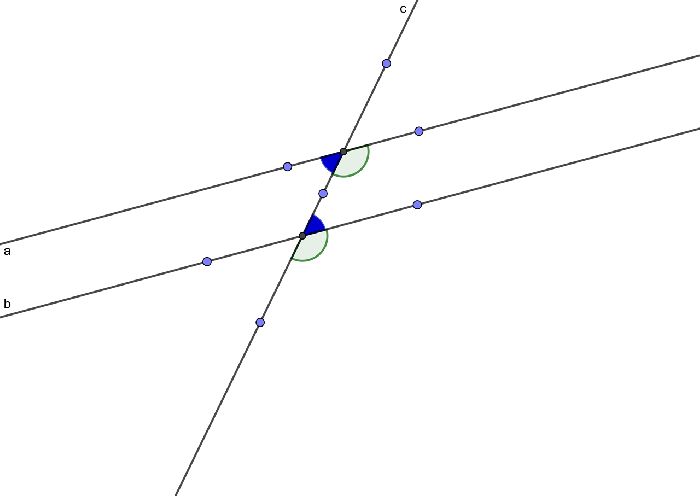
Рис. 3. Иллюстрация признаков.
Что мы узнали?
Мы дали понятие параллельным прямым, выделили две большие группы свойств параллельных прямых и доказали два свойства. Разобрались с использованием аксиомы параллельных прямых при доказательстве теорем в геометрии.
Тест по теме
Оценка статьи
Средняя оценка: 4.3. Всего получено оценок: 94.
Источник
Параллельные прямые – подарок судьбы в решении многих задач.
Они дают тебе множество равных углов! И на них основывается много признаков фигур.
Что, безусловно, будет очень полезно.
Читай эту статью – будешь знать о них все!
И получишь заслуженные баллы на ЕГЭ.
Прямые называются параллельными, если они лежат в одной плоскости и не пересекаются, сколько бы их не продолжали.
Вот, как рельсы

Принято обозначение:
( displaystyle a//b) – читается как ( displaystyle a) параллельна ( displaystyle b).
Самым важным фактом, который нужно принять без доказательства (не только тебе, но и любому математику) для того, чтобы вся геометрия не развалилась и не превратилась в какую-то неузнаваемую теорию, является так называемая «аксиома параллельных прямых».
Часто ее еще называют «пятый постулат Евклида». Формулируем:
Через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.

Смотри: через любую точку ( displaystyle A) проходит только одна прямая ( displaystyle b), которая параллельна ( displaystyle a), все остальные будут пересекать прямую ( displaystyle a).
Казалось бы: чего проще – ну, одна так одна…
Но ты себе просто не представляешь, сколько споров вели математики на протяжении прямо-таки тысячелетий, прежде чем осознали истинную роль этой аксиомы о параллельных прямых.
В конце концов, уже в 19-м веке, после открытий Лобачевского, Гаусса и других ученых стало ясно, что можно построить и другие виды геометрии, в которых не выполняется аксиома параллельных прямых, в которых ее можно выбросить, но эти геометрии уже оказываются не геометриями плоскости, а геометриями на каких-то хитрых поверхностях.
А наша привычная плоскость оттого и называется евклидовой, что при построении геометрии на ней, при решении всех задачек и доказательстве теорем мы считаем этот многострадальный пятый постулат Евклида выполнимым.
Ну вот, а теперь возникает два вопроса:
1
Если где-то в задаче даны или оказались параллельными две какие-то прямые, то что? Как это использовать?
2
А как вообще узнать, что какие-то прямые параллельны?
Ответ на первый вопрос называется «свойства параллельных прямых», а ответ на второй вопрос называется «признаки параллельных прямых».
Но прежде нам понадобится много названий, которые нужно запомнить, как таблицу умножения.
Итак, ситуация: две прямые пересечены третьей (она называется секущей)
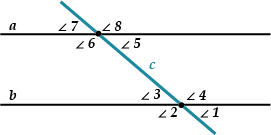
Получается куча углов. Целых ( displaystyle 8) штук.
Приняты такие названия этих углов:
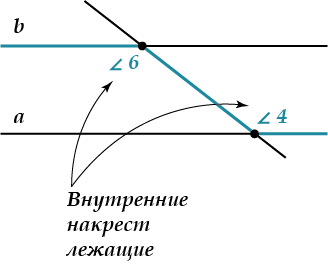
( displaystyle angle 4) и ( displaystyle angle 6) называются внутренними накрест лежащими углами
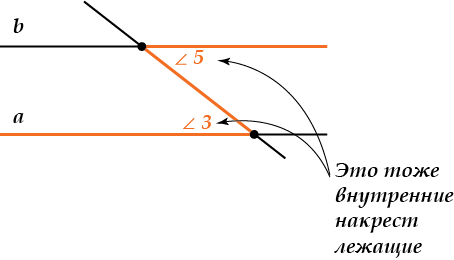
( displaystyle angle 3) и ( displaystyle angle5) – тоже внутренние накрест лежащие углы.
Название говорит само за себя: ( displaystyle angle 4) и ( displaystyle angle 6), так же, как и ( displaystyle angle 3) и ( displaystyle angle5) лежат «накрест» – по разные стороны от секущей и «внутри», между прямыми ( displaystyle a) и ( displaystyle b).
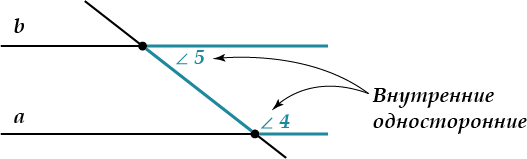
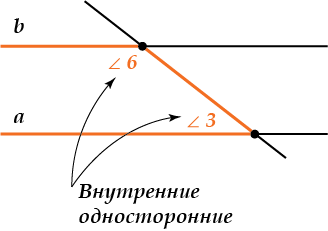
( displaystyle angle 5) и ( displaystyle angle 4) (а еще ( displaystyle angle 6) и ( displaystyle angle 3)) называются внутренними односторонними углами.
Они лежат с одной стороны от секущей и «внутри» между прямыми ( displaystyle a) и ( displaystyle b).
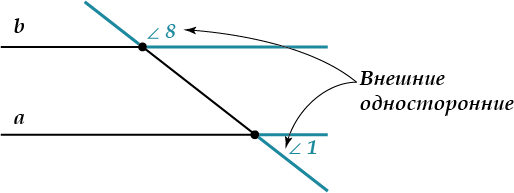
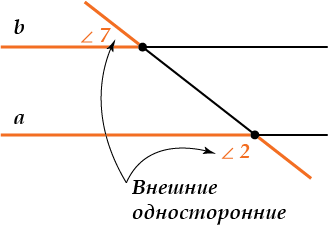
( displaystyle angle 1) и ( displaystyle angle 8) (а еще ( displaystyle angle 2) и ( displaystyle angle 7)) называются внешними односторонними углами (ты уже догадался, почему?)
И последнее название: соответственные углы.
Это пары углов:
- ( displaystyle angle 1) и ( displaystyle angle 5)
- ( displaystyle angle 4) и ( displaystyle angle 8)
- ( displaystyle angle 2) и ( displaystyle angle 6)
- ( displaystyle angle 3) и ( displaystyle angle 7)
Обрати внимание, ( displaystyle angle 1) и ( displaystyle angle 5) лежат в одинаковых «соответственных» местах около точек ( displaystyle A) и ( displaystyle B). То же можно сказать и об остальных перечисленных парах – посмотри на рисунок.
Напоминаем (а то отвлеклись на названия), что пытаемся ответить на вопрос: если ( displaystyle a//b), то что?
И вот что:
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
- Внутренние накрест лежащие углы равны
- Соответственные углы равны
- Сумма любых двух внутренних односторонних равна ( displaystyle 180{}^circ )
Запомни – все задачи с участием слова «параллельность» решаются с помощью этой теоремы о свойствах параллельных прямых.
А теперь, наоборот, признаки параллельных прямых.
То есть, как бы узнать, что прямые параллельны?
Если две прямые (( displaystyle a) и ( displaystyle b)) пересечены третьей и оказалось, что
- Какие-нибудь два накрест лежащих угла равны
ИЛИ - Какие нибудь два соответственных угла равны
ИЛИ - Сумма хоть каких-то двух внутренних односторонних равна ( displaystyle 180{}^circ )
ИЛИ - Сумма хоть каких – то двух внешних односторонних равна ( displaystyle 180{}^circ ),
то прямые ( displaystyle a) и ( displaystyle b) – параллельны
Заметь, что для того, чтобы установить параллельность прямых, достаточно выяснить, скажем, равенство всего двух углов (или накрест лежащих, или соответственных), а уже все остальное окажется , так сказать, бонусом.
Смотри-ка, вот схема:

Параллельные прямые – это прямые, которые лежат в одной плоскости и не пересекаются, сколько бы их не продолжали: ( displaystyle aparallel b).
Секущая – прямая, пересекающая две параллельные прямые: ( displaystyle c).
Аксиома параллельных прямых: через любую точку плоскости, расположенную вне данной прямой, можно провести единственную прямую, параллельную данной.

- ( displaystyle angle 4) и ( displaystyle angle 6), ( displaystyle angle 3) и ( displaystyle angle5)
– внутренние накрест лежащие углы; - ( displaystyle angle 5) и ( displaystyle angle 4), ( displaystyle angle 6) и ( displaystyle angle 3) – внутренние односторонние углы;
- ( displaystyle angle 1) и ( displaystyle angle 8), ( displaystyle angle 2) и ( displaystyle angle 7) – внешние односторонние углы;
- ( displaystyle angle 1) и ( displaystyle angle 5), ( displaystyle angle 4) и ( displaystyle angle 8), ( displaystyle angle 2) и ( displaystyle angle 6), ( displaystyle angle 3) и ( displaystyle angle 7) – соответственные углы.
Свойства параллельных прямых
Если две параллельные прямые пересечены третьей (секущей) прямой, то:
- внутренние накрест лежащие углы равны: ( displaystyle angle 3=angle 5), ( displaystyle angle 4=angle 6);
- соответственные углы равны: ( displaystyle angle 1=angle 5), ( displaystyle angle 4=angle 8), ( displaystyle angle 2=angle 6), ( displaystyle angle 3=angle 7);
- сумма любых двух внутренних односторонних углов равна ( displaystyle 180{}^circ ): ( displaystyle angle 3+angle 6=180{}^circ ), ( displaystyle angle 4+angle 5=180{}^circ );
- сумма любых двух внешних односторонних углов равна ( displaystyle 180{}^circ ): ( displaystyle angle 1+angle 8=180{}^circ ), ( displaystyle angle 2+angle 7=180{}^circ ).
Признаки параллельных прямых

P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Твой час настал!
Параллельные прямые – очень важная тема. Ты будешь встречать их чуть ли не в каждой задаче по геометрии! И они во многом тебе помогут.
А теперь ты знаешь о них все! И справишься с любой задачей!
Как тебе статья? Понравилась? ????
Напиши в комментариях ниже! Все ли было понятно?
Ты можешь задать нам любой вопрос. Мы ответим!
Мы читаем все.
Удачи!
Источник
