Какие свойства параллельных прямых включены в их определение
Свойства параллельных прямых крайне часто встречаются при решении задач и доказательствах теорем. Произвольные прямые – редкость, но есть такие фигуры, как квадрат или параллелограмм, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.

Что такое свойства параллельных прямых
Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.
Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются
Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.
При пересечении двух прямых секущей, образуются накрест лежащие, соответственные и односторонние углы.
Существует аксиома параллельных прямых, которая крайне важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.
Две группы свойств параллельных прямых
Свойств у параллельных прямых всего 5, но они делятся на две большие группы: следствия из аксиомы параллельных прямых и следствия из признаков параллельности прямых. Начнем с первой группы.
Следствия из параллельности прямых
Следствие 1
Если одна из двух параллельных прямых, параллельна третьей, то и другая прямая ей параллельна.
Кажется, что это логично и не требует доказательства. Но в геометрии количество утверждений не требующих обоснования крайне мало и каждое из них носит название аксиомы.
Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.
Проведем две параллельные прямые а и b. Прямая с параллельная прямой а. Предположим, что при этом с не параллельна прямой b. Тогда у нее должна быть какая-то точка пересечения К. То есть через точку К проходит две прямые с и b. При этом каждая из этих прямых должна быть параллельна прямой а.
То есть, через одну точку на плоскости проведены две прямые, параллельные данной. Это невозможно, потому что противоречит аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямые с и b параллельны.
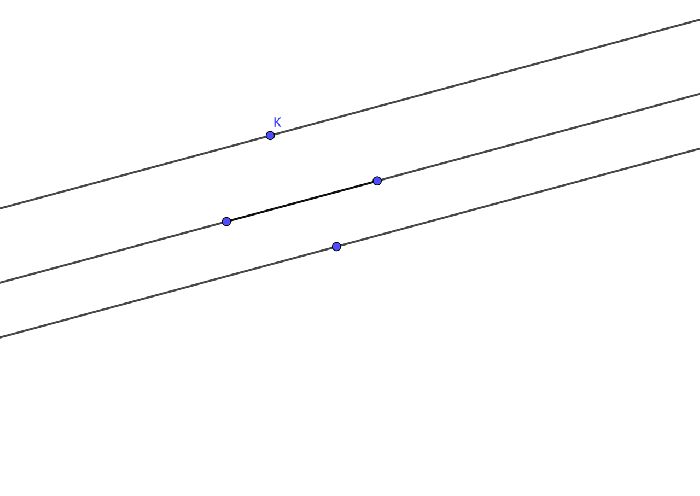
Рис. 1. Иллюстрация следствия.
Следствие 2
Следствие 2 очень важно, так как говорит о секущей двух параллельных прямых. Свойство гласит: если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
Доказательство также ведется методом от противного. Проведем две прямые: а и b. Представим, что прямая с пересекает прямую а, но не пересекает прямую b. Тогда прямые c и b параллельны. При этом с пересекает а, то есть у этих прямых есть общая точка К.
Тогда через точку к проходит прямая а и прямая с, но каждая из них параллельна b. Значит, через одну точку проходит две прямых параллельных прямой b, а это невозможно по аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямая с пересекает каждую из прямых а и b, что и требовалось доказать.
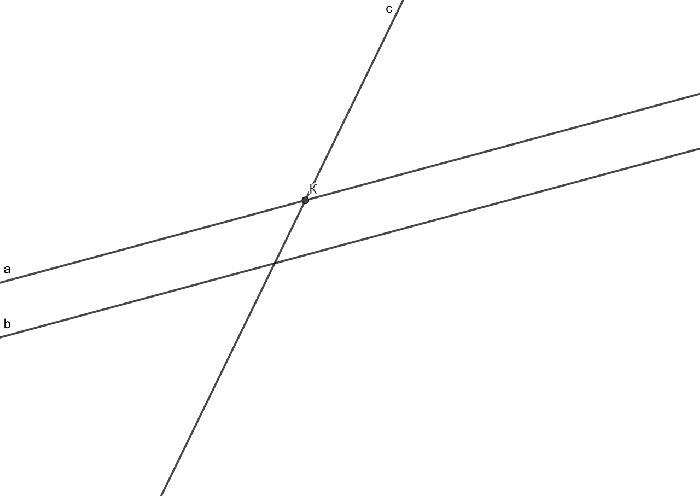
Рис. 2. Рисунок к доказательству.
Следствия из признаков параллельности
Эту группу запомнить проще всего. Свойств параллельности прямых всего 3 и каждому из них соответствует свое следствие.
- Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
- Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180
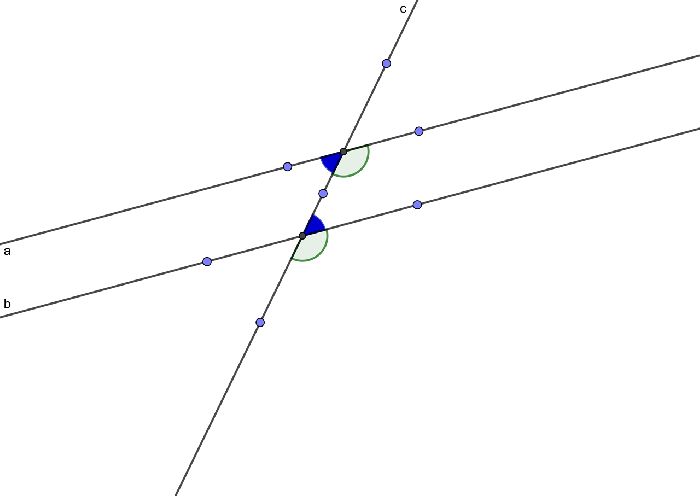
Рис. 3. Иллюстрация признаков.
Что мы узнали?
Мы дали понятие параллельным прямым, выделили две большие группы свойств параллельных прямых и доказали два свойства. Разобрались с использованием аксиомы параллельных прямых при доказательстве теорем в геометрии.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-

Иван Маковецкий
5/5

Иришка Чипрягова
5/5

Елена Иванова
5/5

Константин Никитич
5/5

Манижа Гуломджонова
5/5

Екатерина Лобычева
4/5
Оценка статьи
Средняя оценка: 4.3. Всего получено оценок: 97.
Источник
Сначала рассмотрим разницу между понятиями признак, свойство и аксиома.
Определение 1
Признаком называют некий факт, по которому можно определить истинность суждения об интересующем объекте.
Пример 1
Прямые являются параллельными, если их секущая образует равные накрест лежащие углы.
Определение 2
Свойство формулируется в том случае, когда есть уверенность в справедливости суждения.
Пример 2
При параллельных прямых их секущая образует равные накрест лежащие углы.
Определение 3
Аксиомой называют такое утверждение, которое не требует доказательства и принимается как истина без него.
Каждая наука имеет аксиомы, на которых строятся последующие суждения и их доказательства.
Аксиома параллельных прямых
Иногда аксиому параллельных прямых принимают в качестве одного из свойств параллельных прямых, но вместе с тем на ее справедливости строят другие геометрические доказательства.
Теорема 1
Через точку, которая не лежит на заданной прямой, на плоскости можно провести лишь одну прямую, которая будет параллельной заданной.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Аксиома доказательства не требует.
Свойства параллельных прямых
Теорема 2
Свойство1. Свойство транзитивности параллельности прямых:
Когда одна из двух параллельных прямых является параллельной третьей, то и вторая прямая будет ей параллельна.
Свойства требуют доказательств.
Доказательство:
Пусть имеются две параллельные прямые $a$ и $b$. Прямая $с$ параллельна прямой $а$. Проверим, будет ли в таком случае прямая $с$ параллельна и прямой $b$.
Для доказательства будем пользоваться противоположным суждением:
Представим, что возможен такой вариант, при котором прямая $c$ параллельна одной из прямых, например, прямой $a$, а другую – прямую $b$ – пересекает в некоторой точке $K$.
Получаем противоречие согласно аксиоме параллельных прямых. Получается ситуация, при которой в одной точке пересекаются две прямые, к тому же параллельные одной и той же прямой $a$. Такая ситуация невозможна, следовательно, прямые $b$ и $c$ пересекаться не могут.
Таким образом, доказано, что если одна из двух параллельных прямых является параллельной третьей прямой, то и вторая прямая параллельна третьей прямой.
Теорема 3
Свойство 2.
Если одна из двух параллельных прямых пересекается третьей, то ею будет пересекаться и вторая прямая.
Доказательство:
Пусть имеются две параллельные прямые $а$ и $b$. Также пусть имеется некоторая прямая $с$, которая пересекает одну из параллельных прямых, например, прямую $а$. Необходимо показать, что прямая $с$ пересекает и вторую прямую – прямую $b$.
Построим доказательство методом от противного.
Представим, что прямая $с$ не пересекает прямую $b$. Тогда через точку $К$ проходят две прямые $а$ и $с$, которые не пересекают прямую $b$, т. е. являются параллельными ей. Но такая ситуация противоречит аксиоме параллельных прямых. Значит, предположение было неверным и прямая $с$ пересечет прямую $b$.
Теорема доказана.
Свойства углов, которые образуют две параллельные прямые и секущая:
накрест лежащие углы равны,
соответственные углы равны,
* сумма односторонних углов равна $180^{circ}$.
Пример 3
Даны две параллельные прямые и третья прямая, перпендикулярная одно из них. Доказать, что эта прямая перпендикулярна и другой из параллельных прямых.
Доказательство.
Пусть имеем прямые $а parallel b$ и $с perp а$.
Поскольку прямая $с$ пересекает прямую $а$, то согласно свойству параллельных прямых она будет пересекать и прямую $b$.
Секущая $с$, пересекая параллельные прямые $а$ и $b$, образует с ними равные внутренние накрест лежащие углы.
Т.к. $с perp а$, то углы будут по $90^{circ}$.
Следовательно, $с perp b$.
Доказательство завершено.
Источник
Что такое параллельные прямые в пространстве
Прямые в пространстве могут быть параллельны, пересекаться или скрещиваться. Мы рассмотрим первое свойство.
Впервые теорию о параллельности научно обосновал греческий ученый Евклид в своей работе под названием «Начала».
Определение
Параллельные прямые в пространстве — прямые, лежащие в одной плоскости и не имеющие пересечений друг с другом.

Обозначение параллельных прямых
Сами прямые обозначаются латинскими буквами. Например, l и k. Параллельность обозначается символом: ||
Теорема о параллельных прямых, формулировка
Теорема
Если любая точка в пространстве не расположена на рассматриваемой прямой, то через нее проводима лишь одна прямая, которая будет параллельна рассматриваемой.
Доказательства закона представим в заключительном разделе статьи.

Типы углов при параллельных прямых
Когда прямая пересекает две другие параллельные друг другу прямые, образуется восемь углов. В геометрии они имеют свои названия и свойства. Для дальнейшего разбора темы этой статьи достаточно разобраться в трех видах. Далее при рассмотрении каждого вида в отдельности ориентируйтесь на рисунок ниже:

Односторонние
На рисунке выше это ∠1 и ∠6, а также ∠4 и ∠7. Они расположены с одной стороны относительно прямых.
Соответственные
Углы 2 и 6, 3 и 7, 1 и 5, 4 и 8. Их расположения отличается тем, что они как бы разделены между собой одной из прямых.
Накрест лежащие
На данном рисунке это ∠3 и ∠5, ∠2 и ∠8, ∠1 и ∠7, ∠4 и ∠6. Их расположение легко запомнить, так как они размещаются по принципу «крест-накрест».
Условия параллельности
Чтобы доказать параллельность прямых, нужно знать признаки, по которым она определяется. Достаточно соблюдения хотя бы одного из нижеследующих условий.
Накрест лежащие углы равны

Дано: (a;vertvert b), AB является секущей, углы 1 и 2 — накрест лежащими.
Доказать: равенство ∠1 и ∠2.
Доказательство: допустим, что ∠1 и ∠2 не равные. Тогда проведем угол PAB, причем он будет накрестлежащим с ∠2.

Накрест лежащие углы равны. Из этого следует, что AP (vertvert) b. Но это невозможно, потому что через точку a может проходить только одна прямая, согласно аксиоме, а у нас получилось две — b и A. Поэтому наше предположение неправильное и ∠1=∠2. Ч.т.д.
Соответственные углы равны

∠1 и ∠2 являются соответственными.
Задача

MN (vertvert) AD. Доказать, что( angle NMC=angle BAD).
Решение: (angle NMC=angle DAC) (как соотв.), а (angle DAC=angle BAD) (AD — биссектриса). Следовательно, (angle NMC=angle BAD).
Сумма односторонних углов равна 180 градусов

Сумма ∠1 и ∠2 равна 180º
Доказательство:
a (vertvert) b, поэтому ∠1=∠3 (соотв.). ∠2+∠3=180º (смеж.). Поэтому при сложении получаем 180º.
Если обе прямые параллельны третьей

Этот признак называют также теоремой о трех параллельных прямых на плоскости. Если a (vertvert) b и c (vertvert) b, то a (vertvert) c.
Доказательство
Есть a (vertvert) b. Допустим, что существует еще c (vertvert) a. Согласно условию, a не пересекает b и наоборот.
В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом
Здесь то же самое, что в предыдущем пункте: в случае, когда a и c ||, а b и c также ||, то a и b тоже ||.
Две прямые, перпендикулярные третьей, параллельны

Обозначение перпендикулярных прямых: ⊥
На картинке видно, что a (perp) c и b (perp) c. Отсюда, согласно этому признаку-теореме, следует, что a (vertvert) b.
Доказательство
Допустим, что a (perp) c и b (perp) c, но a не (vertvert;)b. Тогда a и b пересекаются в какой-то точке. Рассмотрим треугольник ABC. Сумма его углов будет равна 180º+∠C. Но так быть не может. Значит, наше предположение неверно, и a (vertvert) b.
Доказательство параллельности прямых
Ниже представлено доказательство теоремы из первого раздела статьи.

- Есть a (прямая) и М (точка, далее — т.). Она не принадлежит a. Через них проходит плоскость альфа ((alpha)). Известно, она единственная.Прямая b проходит через т.М и (vertvert;) а. Она существует, что доказывает аксиома о (;vertvert.)
- Предположим, что существует прямая с, которая тоже проходит через т.М, причем c (vertvert) a. В этом случае потребуется другая плоскость (beta), такая, чтобы прошла через т.М. Такое невозможно, потому что есть теорема, которая говорит, что плоскость только одна. Значит это одна и та же плоскость ((alpha) совпала с (beta)) и одна и та же прямая (b совпал с c). Единственность прямой доказана.
Теорема доказана.
Уравнение параллельной прямой
Если известно, что прямая проходит через какую-то точку с координатами и параллельна другой прямой y=kx+a, то ее уравнение можно найти по формуле:
(gamma-gamma_0=kappaleft(chi-chi_0right))
где k — угловой коэффициент.
Источник
Свойства параллельных прямых крайне часто встречаются при решении задач и доказательствах теорем. Произвольные прямые – редкость, но есть такие фигуры, как квадрат или параллелограмм, где параллельные прямые могут стать основой задачи, а без знания свойств параллельных прямых решить такие задачи невозможно.
Что такое свойства параллельных прямых
Для начала выделим определения, которые необходимо знать для изучения свойств параллельных прямых.
Параллельные прямые это прямые, которые не имеют общих точек, или прямые, которые не пересекаются
Пересечение означает, что у двух объектов есть общая точка или набор точек. Поэтому когда в геометрии говорят, что прямые имеют общую точку, имеется в виду, что они пересекаются.
При пересечении двух прямых секущей, образуются накрест лежащие, соответственные и односторонние углы.
Существует аксиома параллельных прямых, которая крайне важна при доказательстве некоторых свойств и является основным свойством параллельных прямых. Аксиома гласит, что через точку на плоскости можно провести только одну прямую, параллельную данной.
Две группы свойств параллельных прямых
Свойств у параллельных прямых всего 5, но они делятся на две большие группы: следствия из аксиомы параллельных прямых и следствия из признаков параллельности прямых. Начнем с первой группы.
Следствия из параллельности прямых
Следствие 1
Если одна из двух параллельных прямых, параллельна третьей, то и другая прямая ей параллельна.
Кажется, что это логично и не требует доказательства. Но в геометрии количество утверждений не требующих обоснования крайне мало и каждое из них носит название аксиомы.
Аксиомы были выведены еще на заре геометрии и с тех пор мало что изменилось. Большая часть современных теорем выведена на основании аксиом Древней Греции. Эти утверждения единственные, что в математике не требует доказательства.
Проведем две параллельные прямые а и b. Прямая с параллельная прямой а. Предположим, что при этом с не параллельна прямой b. Тогда у нее должна быть какая-то точка пересечения К. То есть через точку К проходит две прямые с и b. При этом каждая из этих прямых должна быть параллельна прямой а.
То есть, через одну точку на плоскости проведены две прямые, параллельные данной. Это невозможно, потому что противоречит аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямые с и b параллельны.
Рис. 1. Иллюстрация следствия.
Следствие 2
Следствие 2 очень важно, так как говорит о секущей двух параллельных прямых. Свойство гласит: если прямая пересекает одну из параллельных прямых, то она пересечет и вторую.
Доказательство также ведется методом от противного. Проведем две прямые: а и b. Представим, что прямая с пересекает прямую а, но не пересекает прямую b. Тогда прямые c и b параллельны. При этом с пересекает а, то есть у этих прямых есть общая точка К.
Тогда через точку к проходит прямая а и прямая с, но каждая из них параллельна b. Значит, через одну точку проходит две прямых параллельных прямой b, а это невозможно по аксиоме параллельных прямых. Значит изначальное предположение было неверным и прямая с пересекает каждую из прямых а и b, что и требовалось доказать.
Рис. 2. Рисунок к доказательству.
Следствия из признаков параллельности
Эту группу запомнить проще всего. Свойств параллельности прямых всего 3 и каждому из них соответствует свое следствие.
- Прямые параллельны, если накрест лежащие углы при секущей равны. Следствие вполне логично: Накрест лежащие углы при двух параллельных прямых и секущей равны.
- Прямые параллельны, если соответственные углы равны. Следствие: соответственные углы при параллельных прямых и секущей равны.
- Прямые параллельны, если сумма односторонних углов равна 180. Следствие: сумма односторонних углов при параллельных прямых и секущей равны 180
Рис. 3. Иллюстрация признаков.
Что мы узнали?
Мы дали понятие параллельным прямым, выделили две большие группы свойств параллельных прямых и доказали два свойства. Разобрались с использованием аксиомы параллельных прямых при доказательстве теорем в геометрии.
Предыдущая
ГеометрияПризнаки параллельных прямых – определение параллельности
Следующая
ГеометрияБиссектриса равнобедренного треугольника, ее свойства
Источник
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Определение 1
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.

Определение 2
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
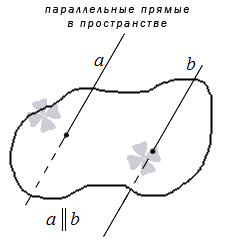
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Чтобы обозначить параллельность прямых, общепринято использовать символ ∥. Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b. Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b, или прямая b параллельна прямой а.
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Аксиома
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Теорема 1
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10-11 классов).
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Определение 3
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:

Теорема 2
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:

Доказательство указанных условий присутствует в программе геометрии за 7-9 классы.
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
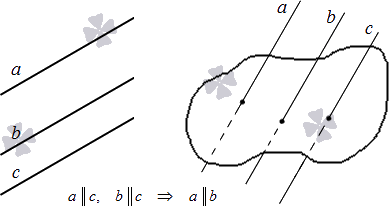
Теорема 3
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
Теорема 4
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
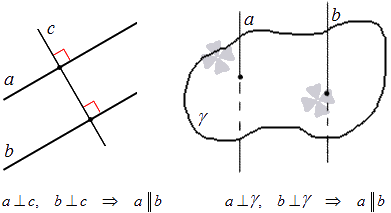
Теорема 5
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
Теорема 6
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Проиллюстрируем:
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Теорема 7
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a→=(ax, ay) и b→=(bx, by) являются направляющими векторами прямых a и b;
и nb→=(nbx, nby) являются нормальными векторами прямых a и b, то указанное выше необходимое и достаточное условие запишем так: a→=t·b→⇔ax=t·bxay=t·by или na→=t·nb→⇔nax=t·nbxnay=t·nby или a→, nb→=0⇔ax·nbx+ay·nby=0, где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
- Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A1x+B1y+C1=0; прямая b – A2x+B2y+C2=0. Тогда нормальные векторы заданных прямых будут иметь координаты (А1, В1) и (А2, В2) соответственно. Условие параллельности запишем так:
A1=t·A2B1=t·B2
- Прямая a описывается уравнением прямой с угловым коэффициентом вида y=k1x+b1. Прямая b – y=k2x+b2. Тогда нормальные векторы заданных прямых будут иметь координаты (k1, -1) и (k2, -1) соответственно, а условие параллельности запишем так:
k1=t·k2-1=t·(-1)⇔k1=t·k2t=1⇔k1=k2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
- Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x-x1ax=y-y1ay и x-x2bx=y-y2by или параметрическими уравнениями прямой на плоскости: x=x1+λ·axy=y1+λ·ay и x=x2+λ·bxy=y2+λ·by.
Тогда направляющие векторы заданных прямых будут: ax, ay и bx, by соответственно, а условие параллельности запишем так:
ax=t·bxay=t·by
Разберем примеры.
Пример 1
Заданы две прямые: 2x-3y+1=0 и x12+y5=1. Необходимо определить, параллельны ли они.
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
x12+y5=1⇔2x+15y-1=0
Мы видим, что na→=(2, -3) – нормальный вектор прямой 2x-3y+1=0, а nb→=2, 15- нормальный вектор прямой x12+y5=1.
Полученные векторы не являются коллинеарными, т.к. не существует такого значения t, при котором будет верно равенство:
2=t·2-3=t·15⇔t=1-3=t·15⇔t=1-3=15
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Пример 2
Заданы прямые y=2x+1и x1=y-42. Параллельны ли они?
Решение
Преобразуем каноническое уравнение прямой x1=y-42 к уравнению прямой с угловым коэффициентом:
x1=y-42⇔1·(y-4)=2x⇔y=2x+4
Мы видим, что уравнения прямых y = 2x + 1 и y = 2x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2x + 1, например, (0, 1), координаты этой точки не отвечают уравнению прямой x1=y-42, а значит прямые не совпадают.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Нормальный вектор прямой y = 2x + 1 это вектор na→=(2, -1), а направляющий вектором второй заданной прямой является b→=(1, 2). Скалярное произведение этих векторов равно нулю:
na→, b→=2·1+(-1)·2=0
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Теорема 8
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a→=(ax, ay, az) и b→=(bx, by, bz)являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t, чтобы выполнялось равенство:
a→=t·b→⇔ax=t·bxay=t·byaz=t·bz
Пример 3
Заданы прямые x1=y-20=z+1-3 и x=2+2λy=1z=-3-6λ. Необходимо доказать параллельность этих прямых.
Решение
Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a→ и b→ заданных прямых имеют координаты: (1, 0, -3) и (2, 0, -6).
Так как:
1=t·20=t·0-3=t·-6⇔t=12, то a→=12·b→.
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
Источник
