Какие свойства определяются при испытании на растяжение

Испытание на растяжение металла заключаются в растяжении образца с построением графика зависимости удлинения образца (Δl) от прилагаемой нагрузки (P), с последующим перестроением этой диаграммы в диаграмму условных напряжений (σ – ε)

Испытания на растяжение проводятся по ГОСТ 1497, по этому же ГОСТу определяются и образцы на которых проводятся испытания.

Образцы для испытания на растяжение Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:

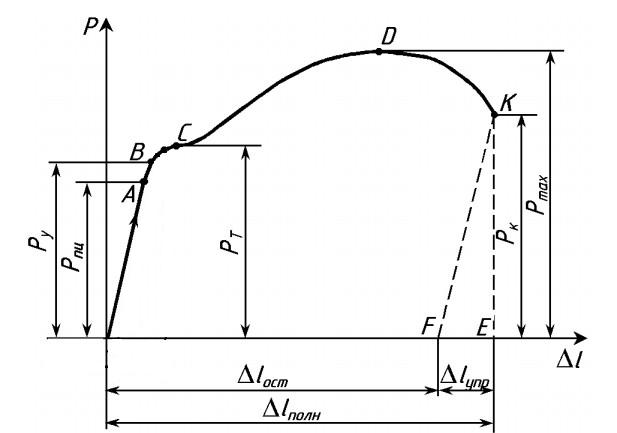
Испытание на растяжение

Участок ОА – участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
Участок ОВ – участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении

Выше точки В диаграмма растяжения отходит от прямой – деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.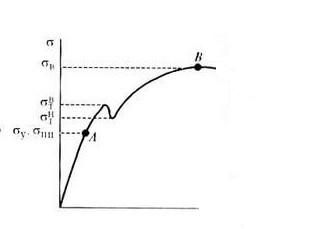
Зуб текучести на диаграмме растяжения металла Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.

После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение – шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.

Прилагаемая нагрузка для растяжения образца зависит от геометрии этого образца. Чем больше площадь сечения, тем более высокая нагрузка необходима для растяжения образца. По этой причине, получаемая машинная диаграмма не дает качественной оценки механических свойств материала. Чтобы исключить влияние геометрии образца, машинную диаграмму перестраивают в координатах σ − ε путем деления ординат P на первоначальную площадь сечения образца A0 и абсцисс ∆l на lо. Перестроенная таким образом диаграмма называется диаграммой условных напряжений. Уже по этой, новой диаграмме, определяют механические характеристики материала.

Определяются следующие механические характеристики:

Предел пропорциональности σпц – наибольшее напряжение, после которого нарушается справедливость закона Гука σ = Еε , где Е – модуль продольной упругости, или модуль упругости первого рода. При этом Е =σ/ε = tgα , т. е. модуль E это тангенс угла наклона прямолинейной части диаграммы к оси абсцисс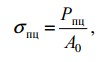 Формула определения предела пропорциональности

Предел упругости σу — условное напряжение, соответствующее появлению остаточных деформаций определенной заданной величины (0,05; 0,001; 0,003; 0,005%); допуск на остаточную деформацию указывается в индексе при σу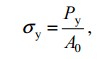 Формула определения предела упругости

Предел текучести σт – напряжение, при котором происходит увеличение деформации без заметного увеличения растягивающей нагрузки

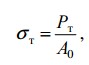Формула расчета предела текучести Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести

Предел прочности (временное сопротивление разрыву) σв – напряжение, соответствующее наибольшей нагрузке Pmax , предшествующей разрыву образца

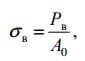
Формула расчета предела прочности

Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности – относительное удлинение δ и относительное сужение ψ

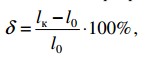
Формула расчета относительного удлинения

где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца

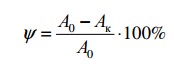
Формула расчета относительного сужения образца

Площади поперечного сечения образца

Изопропиловый спирт цена за тонну оптом – https://www.dcpt.ru

Источник

Лабораторная работа № 1

Цель работы – изучить поведение малоуглеродистой стали при растяжении и определить ее механические характеристики.

Основные сведения

Испытания на растяжение являются основным и наиболее распространенным методом лабораторного исследования и контроля механических свойств материалов.

Эти испытания проводятся и на производстве для установления марки поставленной заводом стали или для разрешения конфликтов при расследовании аварий.

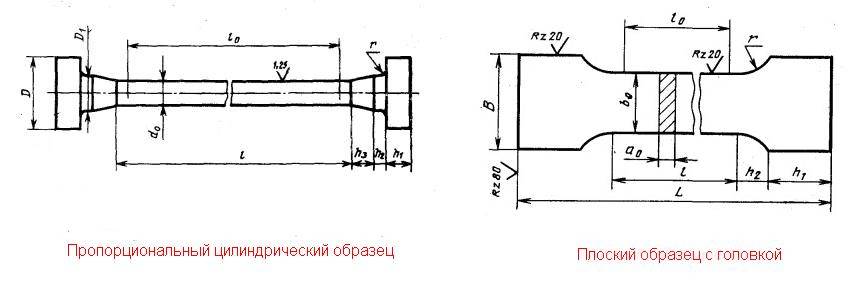
В таких случаях, кроме металлографических исследований, определяются главные механические характеристики на образцах, взятых из зоны разрушения конструкции. Образцы изготавливаются по ГОСТ 1497-84 и могут иметь различные размеры и форму (рис. 1.1).

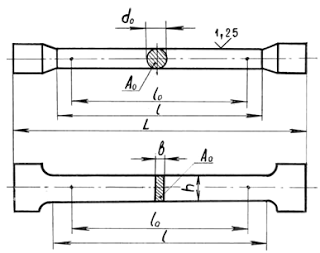
Образцы для испытания на растяжение

Рис. 1.1. Образцы для испытания на растяжение

Между расчетной длиной образца lо и размерами поперечного сечения Ао (или dо для круглых образцов) выдерживается определенное соотношение:

В испытательных машинах усилие создается либо вручную — механическим приводом, либо гидравлическим приводом, что присуще машинам с большей мощностью.

В данной работе используется универсальная испытательная машина УММ-20 с гидравлическим приводом и максимальным усилием 200 кН, либо учебная универсальная испытательная машина МИ-40КУ (усилие до 40 кН).

Порядок выполнения и обработка результатов

Образец, устанавливаемый в захватах машины, после включения насоса, создающего давление в рабочем цилиндре, будет испытывать деформацию растяжения. В измерительном блоке машины есть шкала с рабочей стрелкой, по которой мы наблюдаем рост передаваемого усилия F.

Зависимость удлинения рабочей части образца от действия растягивающей силы во время испытания отображается на миллиметровке диаграммного аппарата в осях F-Δl (рис. 1.2).

В начале нагружения деформации линейно зависят от сил, потому участок I диаграммы называют участком пропорциональности. После точки В начинается так называемый участок текучести II.

На этой стадии стрелка силоизмерителя как бы спотыкается, приостанавливается, от точки В на диаграмме вычерчивается либо прямая, параллельная горизонтальной оси, либо слегка извилистая линия — деформации растут без увеличения нагрузки. Происходит перестройка структуры материала, устраняются нерегулярности в атомных решетках.

Далее самописец рисует участок самоупрочнения III. При дальнейшем увеличении нагрузки в образце происходят необратимые, большие деформации, в основном концентрирующиеся в зоне с макронарушениями в структуре – там образуется местное сужение — «шейка».

На участке IV фиксируется максимальная нагрузка, затем идет снижение усилия, ибо в зоне «шейки» сечение резко уменьшается, образец разрывается.

При нагружении на участке I в образце возникают только упругие деформации, при дальнейшем нагружении появляются и пластические — остаточные деформации.

Если в стадии самоупрочнения начать разгружать образец (например, от т. С), то самописец будет вычерчивать прямую СО1. На диаграмме фиксируются как упругие деформации Δlу (О1О2), так и остаточные Δlост (ОО1). Теперь образец будет обладать иными характеристиками.

Так, при новом нагружении этого образца будет вычерчиваться диаграмма О1CDЕ, и практически это будет уже другой материал. Эту операцию, называемую наклеп, широко используют, например, в арматурных цехах для улучшения свойств проволоки или арматурных стержней.

Диаграмма растяжения (рис. 1.2) характеризует поведение конкретного образца, но отнюдь не обобщенные свойства материала. Для получения характеристик материала строится условная диаграмма напряжений, на которой откладываются относительные величины – напряжения σ=F/A0 и относительные деформации ε=Δl/l0 (рис. 1.3), где А0, l0 – начальные параметры образца.

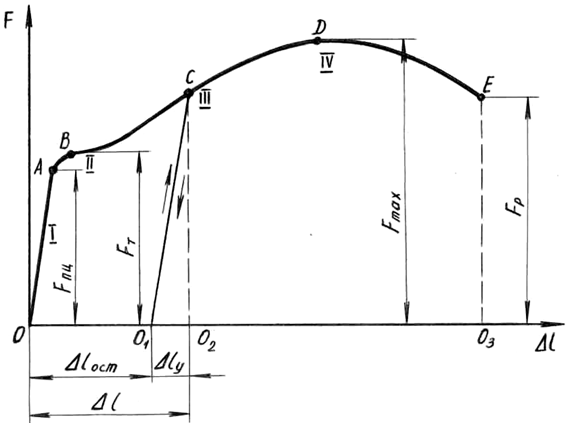
Диаграмма растяжения образца из малоуглеродистой стали

Рис. 1.2. Диаграмма растяжения образца из малоуглеродистой стали

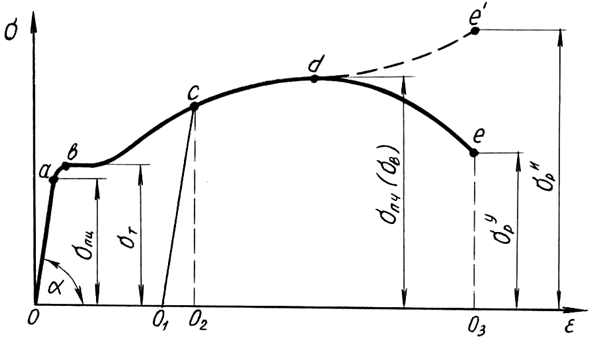
Условная диаграмма напряжений при растяжении

Рис. 1.3. Условная диаграмма напряжений при растяжении

Условная диаграмма напряжений при растяжении позволяет определить следующие характеристики материала (рис. 1.3):

σпц – предел пропорциональности – напряжение, превышение которого приводит к отклонению от закона Гука. После наклепа σпц может быть увеличен на 50-80%;

σу – предел упругости – напряжение, при котором остаточное удлинение достигает 0,05%. Напряжение σу очень близко к σпц и обнаруживается при более тонких испытаниях. В данной работе σу не устанавливается;

σт – предел текучести – напряжение, при котором происходит рост деформаций при постоянной нагрузке.

Иногда явной площадки текучести на диаграмме не наблюдается, тогда определяется условный предел текучести, при котором остаточные деформации составляют ≈0,2% (рис. 1.4);

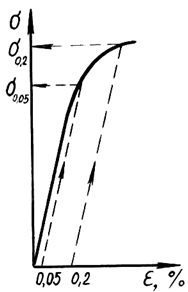
Определение предела упругости и условного предела текучести

Рис. 1.4. Определение предела упругости и условного предела текучести

σпч (σв) – предел прочности (временное сопротивление) – напряжение, соответствующее максимальной нагрузке;

σр – напряжение разрыва. Определяется условное σур и истинное σир=Fр/Аш, где Аш – площадь сечения «шейки» в месте разрыва.

Определяются также характеристики пластичности – относительное остаточное удлинение

δ = (l1 – l0)∙100% / l0,

где l1 – расчетная длина образца после разрыва,
и относительное остаточное сужение

ψ = (А0 — Аш)∙100% / А0.

По диаграмме напряжений можно приближенно определить модуль упругости I рода

E=σпц/ε=tgα,

причем после операции наклепа σпц возрастает на 20-30%.

Работа, затраченная на разрушение образца W, графически изображается на рис. 1.2 площадью диаграммы OABDEO3. Приближенно эту площадь определяют по формуле:
W = 0,8∙Fmax∙Δlmax.

Удельная работа, затраченная на разрушение образца, говорит о мере сопротивляемости материала разрушению w = W/V, где V = A0∙l0 – объем рабочей части образца.

По полученным прочностным и деформационным характеристикам и справочным таблицам делается вывод по испытуемому материалу о соответствующей марке стали

Контрольные вопросы

Изобразите диаграмму растяжения образца из малоуглеродистой стали (Ст.3). Покажите полные, упругие и остаточные абсолютные деформации при нагружении силой, большей, чем Fт.
На каком участке образца происходят основные деформации удлинения? Как это наблюдается на образце? Какие нагрузки фиксируются в этот момент?
Объясните, почему после образования шейки дальнейшее растяжение происходит при все уменьшающейся нагрузке?
Перечислите механические характеристики, определяемые в результате испытаний материала на растяжение. Укажите характеристики прочности и пластичности.
Дайте определение предела пропорциональности.
Дайте определение предела упругости.
Дайте определение предела текучести.
Дайте определение предела прочности.
Как определить предел текучести при отсутствии площадки текучести? Покажите, как это сделать, по конкретной диаграмме.
Какие деформации называются упругими, какие остаточными? Укажите их на полученной в лабораторной работе диаграмме растяжения стали.
Как определяется остаточная деформация после разрушения образца?
Выделите на диаграмме растяжения образца из мягкой стали упругую часть его полного удлинения для момента действия максимальной силы.
Какое явление называется наклепом? До какого предела можно довести предел пропорциональности материалов с помощью наклепа?
Как определяется работа, затраченная на разрушение образца? О каком свойстве материала можно судить по удельной работе, затраченной на разрушение образца?
Как определить марку стали и допускаемые напряжения для нее после проведения лабораторных испытаний?
Чем отличается диаграмма истинных напряжений при растяжении от условной диаграммы?
Можно ли определить модуль упругости материала по диаграмме напряжений?
Как определить работу, затрачиваемую на деформации текучести лабораторного образца?

Испытание материалов на сжатие >
Краткая теория >
Примеры решения задач >

Источник

Отвечает эксперт ЗАО ЦНИИПСК им. Мельникова

Как уже говорилось выше, при испытаниях строится диаграмма растяжения металла. На ней есть несколько характерных участков:

Участок ОА — участок пропорциональности между нагрузкой Р и удлинением ∆l. Это участок, на котором сохраняется закон Гука. Данная пропорциональность была открыта Робертом Гуком в 1670 г. и в дальнейшем получила название закона Гука.
Участок ОВ — участок упругой деформации. Т.е., если к образцу приложить нагрузку, не превышающую Ру, а потом разгрузить, то при разгрузке деформации образца будут уменьшаться по тому же закону, по которому они увеличивались при нагружении

Выше точки В диаграмма растяжения отходит от прямой — деформация начинает расти быстрее нагрузки, и диаграмма принимает криволинейный вид. При нагрузке, соответствующей Рт (точка С ), диаграмма переходит в горизонтальный участок. В этой стадии образец получает значительное остаточное удлинение практически без увеличения нагрузки. Получение такого участка на диаграмме растяжения объясняется свойством материала деформироваться при постоянной нагрузке. Это свойство называется текучестью материала, а участок диаграммы растяжения, параллельный оси абсцисс, называется площадкой текучести.

Иногда площадка текучести носит волнообразный характер. Это чаще касается растяжения пластичных материалов и объясняется тем, что вначале образуется местное утонение сечения, затем это утонение переходит на соседний объем материала и этот процесс развивается до тех пор, пока в результате распространения такой волны не возникает общее равномерное удлинение, отвечающее площадке текучести. Когда имеется зуб текучести, при определении механических свойств материала, вводят понятия о верхнем и нижнем пределах текучести.

После появления площадки текучести, материал снова приобретает способность сопротивляться растяжению и диаграмма поднимается вверх. В точке D усилие достигает максимального значения Pmax. При достижении усилия Pmax на образце появляется резкое местное сужение — шейка. Уменьшение площади сечения шейки вызывает падение нагрузки и в момент, соответствующий точке K диаграммы, происходит разрыв образца.

Определяются следующие механические характеристики:

Также выделяют условный предел текучести — это условное напряжение, при котором остаточная деформация достигает определенной величины (обычно 0,2% от рабочей длины образца; тогда условный предел текучести обозначают как σ0,2). Величину σ0,2 определяют, как правило, для материалов, у которых на диаграмме отсутствует площадка или зуб текучести

Кроме характеристик прочности материала, при испытании на растяжение определяют также характеристики пластичности — относительное удлинение δ и относительное сужение ψ

где lо – первоначальная расчетная длина образца, а lк – конечная расчетная длина образца

Источник

Механических свойств

Механические испытания при кратковременных испытаниях применяются для оценки прочности деталей и конструкций, подвергающихся быстро нарастающим нагрузкам, и для определения механических свойств пластически деформируемых металлов и сплавов. Как правило, основные испытания материалов проводят в соответствии с ГОСТами, которые устанавливают методы испытаний, определяемые механические характеристики, требования к используемому оборудованию, типы и размеры испытываемых образцов и последовательность их нагружения, порядок обработки результатов испытания и оценки достоверности полученных результатов.

Статическое испытание на растяжение – наиболее распространенный метод механических испытаний конструкционных материалов. Это связано с простотой процедуры, наличием большого парка соответствующего оборудования и высокой практической ценностью получаемой при этом информации, используемой для оценки механического поведения материалов при разных видах нагружения. При испытаниях определяют характеристики прочности и характеристики пластичности. Для получения этих характеристик чаще всего используют универсальные испытательные машины, на которых испытывают на растяжение специально изготовленные образцы. Характер испытаний, применяемые образцы и т.д. стандартизированы. Например, испытания на растяжение при комнатной температуре соответствуют требованиям ГОСТ 1497-84.

При осевом растяжении образца реализуется одноосное напряженное состояние, при котором Ϭ1 = Ϭmax, Ϭ2 = Ϭ3 = 0, максимальное касательное напряжение τmax = Ϭmax /2 и действует в площадках, ориентированных под углом 45о к направлению Ϭ1. (Рис. ).

Обобщенной характеристикой сопротивления металлов деформированию является диаграмма деформирования, которая строится в координатах Ϭ – ε(Рис.11. ) и отражает этапы упругого и упругопластического деформирования до полного разрушения образца. При этом Ϭ определяется условно делением нагрузки Р в данный момент нагружения на начальную площадь сечения образца F0, а ε – делением текущего значения абсолютного удлинения образца ∆ℓна начальную его длину ℓ0. Большинство стандартных прочност-

ных характеристик рассчитывают по положению определенных точек на этой диаграмме в виде условных растягивающих напряжений.

На практике же в соответствии с требованиями стандарта при растяжении образца графически фиксируется зависимость между приложенным усилием и абсолютным удлинением образца, т.е. механические свойства обычно определяют по первичным кривым растяжения в координатах Р – ∆ℓ (Рис.11. ), которые автоматически записываются на диаграммной ленте или в памяти компьютера.

Если же нагрузку относить к действительному в данный момент сечению, то получают значения истинных напряжений. Диаграммы истинных напряжений определять сложнее, но они дают представление о физических процессах, протекающих в материале в процессе деформации и имеют особое значение для прочностных расчетов и технологии обработки металлов давлением. Например, истинные напряжения при разрушении различных материалов и разных структурных состояниях весьма значительно отличаются.

При испытаниях на растяжение можно определить несколько характеристик прочности и пластичности.

1. Предел пропорциональности σпц –отвечает напряжению, при котором отклонение от линейной зависимости между нагрузкой и удлинением достигает такой величины, что тангенс угла наклона, образованного касательной к кривой нагрузка – удлинение в точке Рпц с осью нагрузок увеличивается на 50% от своего значения на упругом участке. На рис.12.7 показано определение σпцграфическим способом. Из начала координат диаграммы деформации

2. Предел упругости Ϭ0.05 – напряжение, при котором остаточное удлинение достигает 0.05% длины участка образца, равного базе тензометра. Размер этого участка на стандартных (по ГОСТ 1497-84) образцах Ф10 мм равен пятикратному диаметру, т.е. 50 мм, и при изготовлении образца фиксируется кернами на боковой поверхности (Рис.12.7).

Предел упругости Ϭ0.05 можно определить графическим способом на диаграмме деформации в координатах Р – ∆ℓ. Для этого нужно знать масштаб оси деформаций диаграммы (М). На начальном участке диаграммы деформации (Рис.12.8) откладываем в мм размер, равный 50х0.05%хМ (отрезок ОЕ), и проводим линию ЕР, параллельную упругому участку ОА. Координата точки Р на оси ординат соответствует нагрузке Р0.05. Предел упругости Ϭ0.05 определяют по формуле:

Ϭ0.05 = Р0.05 /F0 ,,

где F0 – площадь первоначального сечения рабочей части образца. Масштаб М можно рассчитать по диаграмме. Для этого необходимо измерить на испытанном образце абсолютное удлинение ∆ℓ и определить на диаграмме длину участка, соответствующую ∆ℓ.Разделив эту длину на ∆ℓ получаем величину масштаба М.

3. Предел текучести ϬТ. Различают физический и условный предел текучести. Физический предел текучести определяют на материалах, диаграммы растяжения которых имеют ярко выраженные зуб и площадку текучести (Кривые 2 и 3 на рис.12.9). На таких материалах определяют: Верхний предел текучести ϬТВ – напряжение, соответствующее верхнему пику нагрузки до начала текучести образца. Нижний предел текучести ϬТН – напряжение, при котором образец деформируется без заметного увеличения нагрузки.

Большинство диаграмм деформации конструкционных сталей и других технических материалов не имеют ярко выраженной площадки текучести. Для них определяют условный предел текучести Ϭ0.2 – напряжение, при котором остаточное удлинение достигает 0.2% длины рабочей части участка между кернами. Ϭ0.2можно определить графически (Рис.12.10) по той же методике, что и Ϭ0.05. При этом условный предел текучести определяется по формуле Ϭ0.2 = Р0.2 /F0.

4. Модуль упругости – физическое свойство материала, характеризующее его упругие свойства. Различают модуль упругости при растяжении– Е и модуль упругости при сдвиге – G. Так как модуль упругости – это фактически приращение напряжения к соответствующему удлинению в пределах упругой области, то Модуль упругости при растяжении – Е можно определить графически на диаграмме деформации. При этом модуль упругости определяют по формуле:

Е = ∆Рх ℓ0 /∆ℓср х F0,

где ∆Р– приращение нагрузки на линейном участке диаграммы, ℓ0– начальная расчетная длина образца (50 мм), ∆ℓср– приращение удлинения (с учетом масштаба М), F0 – площадь первоначального сечения рабочей части образца.

5. Предел прочности (временное сопротивление) – ϬВ – напряжение, соответствующее наибольшей нагрузке Рmax, предшествующей разрыва образца. Временное сопротивление вычисляют по формуле ϬВ = Рmax / F0.

При испытаниях на растяжение можно определить не только характеристики прочности но и пластичность. Характеристиками пластичности являются относительное удлинение δ и относительное сужение ψ.

6. Относительное удлинение (после разрыва) δ – это характеристика пластичности материала, равная отношению удлинения в момент разрушения к начальной расчетной длине образца, выраженная в процентах. Относительное удлинение определяется по формуле:

δ = [(ℓк – ℓ0) / ℓ0]х 100 (%),

где ℓк – длина расчетной части образца (между кернами) в момент разрушения.

7. Относительное сужение (после разрыва) ψ –это отношение разницы между площадью первоначального сечения образца F0 и площадью его минимального сечения в момент разрушения (в шейке) Fкк площади первоначального сечения образца F0, выраженная в процентах. Относительное удлинение определяется по формуле:

ψ = [(F0 – Fк) / F0]х 100 (%).

8. Истинное сопротивление разрушению Sк – определяется путем деления нагрузки, действовавшей непосредственно перед разрывом образца Рк на площадь сечения в шейке Fк. Истинное сопротивление разрушению Sк характеризует максимальное напряжений в соответствии с диаграммой истинных напряжений.

9. Расчет энергии упругой и пластической деформации осуществляется путем подсчета площадей, расположенных под кривой растяжения (т.е. в координатах Р – ∆ℓ). Этот расчет можно провести для любого момента в процессе разрушения. Упругая энергия Аупр , накопленная в образце, определяется как площадь треугольника между вертикалью из заданной точки и линией, идущей из той же точки параллельно линии нагружения (Рис.11. ). Энергия, затраченная на пластическую деформацию в процессе растяжения Апл, располагается под кривой растяжения слева от этого треугольника.

Дата добавления: 2016-11-02; просмотров: 2186 | Нарушение авторских прав | Изречения для студентов