Какие свойства элементов электрической цепи характеризуют параметры r l c

КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Электрическая цепь
Электрическая цепь и ее характеристики
Электрической цепью называется совокупность электротехнических устройств, создающих замкнутый путь электрическому току. Она состоит из источников (генераторов) энергии, приемников энергии (нагрузки) коммутирующей, измерительной аппаратуры и соединительных проводов.
Заметим, что ЭДС, токи и напряжения, изменяющиеся во времени, обозначаются строчными латинскими буквами е, i, u, а ЭДС, токи и напряжения, неизменные во времени, обозначаются заглавными латинскими буквами E, I, U.
Графическое изображение электрической цепи называется электрической схемой. В схеме различают ветви, узлы и контуры. Ветвь – это часть схемы, состоящая из последовательно соединенных источников, приемников и других элементов цепи, и через них протекает одинаковый ток. Узел – точка схемы, в которой соединены не менее трех ветвей (ветви начинаются и заканчиваются на узлах цепи). Контур – замкнутый путь по элементам схемы.
При расчетах электрических цепей необходимо задаться направлениями токов, напряжений и ЭДС. Эти направления указывают на схемах стрелками.
За направление тока принято направление движения положительных зарядов, т. е. стрелка у тока направлена от большего потенциала к меньшему потенциалу. Направление напряжения в приемнике всегда указывают в ту же сторону, что и у тока
Любая электрическая цепь в общем случае может характеризоваться тремя параметрами: сопротивлением R, индуктивностью L и емкостью С.
Сопротивление R характеризует способность цепи преобразовывать электромагнитную энергию в тепловую.
Величина сопротивления любого элемента цепи определяется как отношение постоянного напряжения на этом элементе к постоянному току в нем и измеряется в омах (Ом):
. (1.1)
Величина, обратная сопротивлению, называется проводимостью. Она обозначается G и измеряется в сименсах (См):
.
Индуктивность L характеризует способность цепи накапливать энергию магнитного поля. Такой способностью обладают любой проводник с током или система проводов.
Эта энергия не преобразуется в тепло, а существует в цепи в виде некоторого запаса энергии. Когда ток в цепи равен нулю, запаса энергии магнитного поля в ней нет.
Величина индуктивности определяется как отношение потокосцепления цепи y к току i и измеряется в генри (Гн):
. (1.2)
Потокосцеплением называется сумма магнитных потоков всех витков катушки. В простейшем случае для катушки на замкнутом стальном сердечнике можно считать, что ее потокосцепление есть магнитный поток Ф, умноженный на число витков w: Y = Ф w.
Емкость С характеризует способность цепи накапливать энергию электрического поля.
Эта энергия не преобразовывается в тепловую энергию, а существует в цепи в виде некоторого запаса. Если напряжение между проводами отсутствует, то и запаса энергии электрического поля в цепи нет.
Величина емкости С определяется как отношение электрического заряда q одного из проводов к напряжению u между ними и измеряется в фарадах (Ф):
. (1.3)
Если R, L и С являются постоянными величинами и не зависят от тока (или напряжения), то такие элементы называются линейными,а цепи, их содержащие, называются линейными цепями.
Элементы, параметры которых зависят от тока или напряжения, называются нелинейными, а цепи, их содержащие, также называются нелиней- ными цепями.
Свойства элементов электрической цепи описываются характеристиками. Для сопротивлений это зависимости напряжения от тока (вольт-амперные характеристики); для индуктивностей это зависимости потокосцепления от тока (вебер-амперные характеристики); для емкостей это зависимости электрического заряда от напряжения (кулонвольтные характеристики).
Cоотношения между током и напряжением в каждом из идеальных элементов цепи называются уравнениями элементов:
; ; .
1.2. Линейные электрические цепи постоянного тока
Дата добавления: 2015-06-04; Просмотров: 3977; Нарушение авторских прав?
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Рекомендуемые страницы:
Читайте также:
Источник
Любая электрическая цепь и каждый ее элемент в отдельности обладают тремя параметрами: сопротивлением R, индуктивностью L и емкостью С.
Сопротивление R характеризует способность цепи преобразовывать электромагнитную энергию в тепловую. Количество тепловой энергии WТ , выделяющееся в сопротивлении R при протекании тока i в течение времени t, определяется соотношением (1.3) и измеряется в джоулях (Дж):
Величина сопротивления любого элемента цепи определяется как отношение постоянного напряжения на этом элементе к постоянному току в нем и измеряется в омах (Ом):
Индуктивность L характеризует способность цепи накапливать энергию магнитного поля. Такой способностью обладает любой проводник с током или система проводов. Количество этой энергии WM , накопленной в цепи, зависит от величины тока i и измеряется в джоулях (Дж):
Эта энергия не преобразуется в тепло, а существует в цепи в виде некоторого запаса. Когда ток в цепи равен нулю, запаса энергии магнитного поля в ней нет.
Величина индуктивности определяется как отношение потокосцепления цепик току i и измеряется в генри (Гн):
Потокосцеплением называется сумма магнитных потоков всех витков катушки. В простейшем случае для катушки на замкнутом стальном сердечнике можно считать, что ее потокосцепление есть магнитный поток Ф, умноженный на число витков w: = Ф w.
38
Емкость С характеризует способность цепи накапливать энергию электрического поля. Такой способностью обладают любые два провода, разделенные диэлектриком, например провод, висящий над землей, любые два провода линии передачи.
Количество энергии электрического поля WЭ , накопленной в цепи с емкостью С, зависит от величины напряжения между проводами и измеряется в джоулях (Дж):
Эта энергия не может преобразовываться в тепловую, а существует в цепи в виде некоторого запаса. Если напряжение между проводами отсутствует, то и запаса энергии электрического поля в цепи нет.
Величина емкости С определяется как отношение электрического заряда q одного из проводов к напряжению u между ними и измеряется в фарадах (Ф):
С q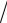 u .
u .
Если R, L и С являются постоянными величинами и не зависят от напряжения), то такие элементы называются линейными, а цепи, содержащие, называются линейными цепями.
Элементы, параметры которых зависят от тока или напряжения, называются нелинейными, а цепи, их содержащие, также называются нелинейными цепями.
Свойства нелинейного элемента электрической цепи не могут быть выражены одним постоянным числом и поэтому описываются его характеристикой. Для сопротивлений это зависимости напряжения от тока (вольтамперные характеристики); для индуктивностей это зависимости потокосцепления от тока (веберамперные характеристики); для емкостей это зависимости электрического заряда от напряжения (кулонвольтные характеристики). На рис. 1.5 показаны примеры характеристик некоторых линейных (ЛЭ) и нелинейных (НЭ) элементов цепи.
Заметим, что характеристики всех линейных элементов цепи являются прямыми линиями, а нелинейных элементов – кривыми.
39
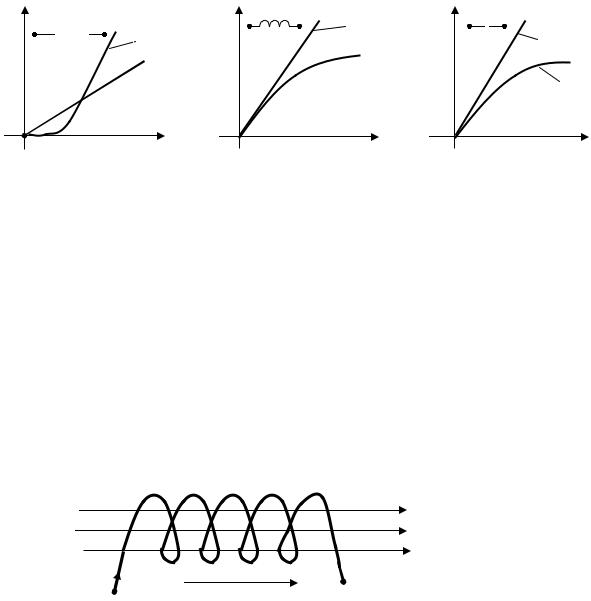
1.6. Идеальные элементы электрической цепи
Любое электротехническое устройство содержит все три параметра: сопротивление R , индуктивность L и емкость С. Рассмотрим (рис. 1.6) катушку, выполненную из провода с конечной проводимостью (это может быть и нить лампы накаливания, и обмотка трансформатора или электродвигателя).
i | R | L | C | q | ||||||||
нэ | лэ | лэ | ||||||||||
нэ | ||||||||||||
лэ | нэ | |||||||||||
u | i | u | ||||||||||
вольтамперная | веберамперная | кулонвольтная | ||||||||||
характеристика | характеристика | характеристика | ||||||||||
сопротивления | индуктивности | емкости | ||||||||||
Рис. 1.5
При подаче на ее зажимы напряжения u на концах катушки появляются разноименные заряды (+)q и ( )q и в обмотке начинает протекать ток i. При этом вокруг витков обмотки возникает магнитное поле, характеризуемое потокосцеплением . Таким образом, в соответствии с формулами (1.4), (1.6) и (1.8) рассматриваемая катушка обладает всеми тремя вышеуказанными параметрами.
R L C
Рис. 1.6
40
Для удобства анализа и расчета электрических цепей вводят в рассмотрение такие элементы, которые при всех условиях обладают только одним параметром: только сопротивлением, только индуктивностью, только емкостью. Они называются идеальными.
Графическое изображение идеальных элементов электрической цепи показано на рис. 1.2 позициями 4, 5 и 6. В природе таких элементов не существует, но есть устройства, по своим свойствам близкие к идеальным. Реостат (резистор) при низких частотах обладает практически только сопротивлением R, а индуктивностью L и емкостью С этого устройства можно пренебречь. Катушка индуктивности на замкнутом ферромагнитном сердечнике с малыми тепловыми потерями в нем обладает на низких частотах практически только индуктивностью L, а сопротивлением R и емкостью С такой катушки можно пренебречь. Конденсатор с малыми внутренними тепловыми потерями обладает практически только емкостью С, а его активной проводимостью G и индуктивностью L можно пренебречь.
Любое реальное электротехническое устройство можно изобразить в виде электрической схемы, состоящей из комбинации идеальных элементов и, следовательно, произвести его электрический расчет.
1.7. Соотношение между током и напряжением в идеальных элементах
цепи
Прежде чем приступать к расчету сколько-нибудь сложных электрических цепей, следует выяснить, каким образом связаны между собой ток и напряжение в каждом из идеальных элементов цепи. Эти соотношения, называемые уравнения элементов, известные из курса физики, приведены
в табл. 1.1. Они имеют всеобщий характер и справедливы для цепей, у которых ток и напряжение изменяются во времени по любому закону.
Из табл. 1.1 видно, что только в сопротивлении R ток и напряжение связаны между собой алгебраическим соотношением. Между током и напряжением в индуктивности и емкости имеют место интегродифференциальные соотношения.
41
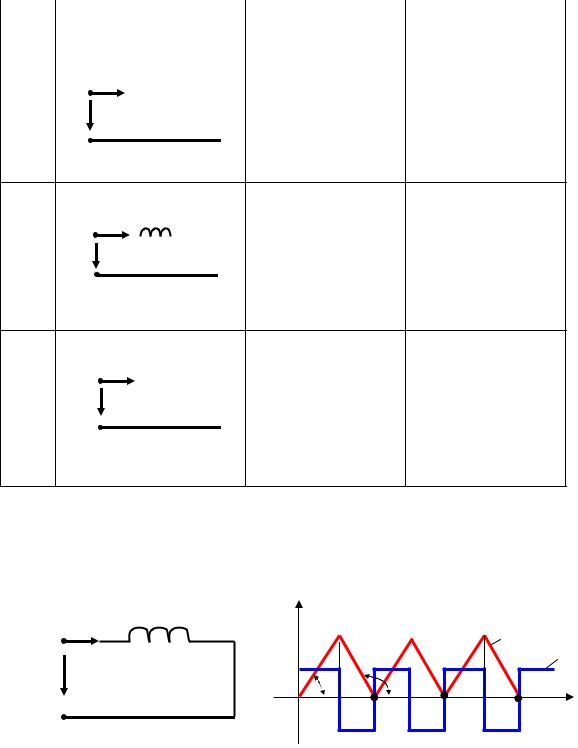
Таблица 1.1
Формулы для определения тока и напряжения в идеальных элементах
№ | Идеальный элемент | Ток | Напряжение | |||||
п/п | ||||||||
i | R | |||||||
i | u | u iR | ||||||
1 | u | |||||||
R | ||||||||
2 | i | L | 1 udt | u L di | ||||
i | ||||||||
dt | ||||||||
u | L | |||||||
3 | i | C | i C du | u 1 idt | ||
u | dt | C | ||||
Пример 1.3. В цепи с идеальной индуктивностью (рис. 1.7,а) действует пилообразный периодический ток (рис. 1.7,б). Требуется определить форму приложенного напряжения.
а) | L | б) | i,u |
i | i | ||
u | |||
u | 1 | 2 | |
t | |||
T | 2T | 3T |
Рис. 1.7
Решение. Для нахождения графика напряжения используем соотношение u L di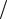 dt , из которого следует, что форма кривой напряжения соответствует производной от тока по времени.
dt , из которого следует, что форма кривой напряжения соответствует производной от тока по времени.
42
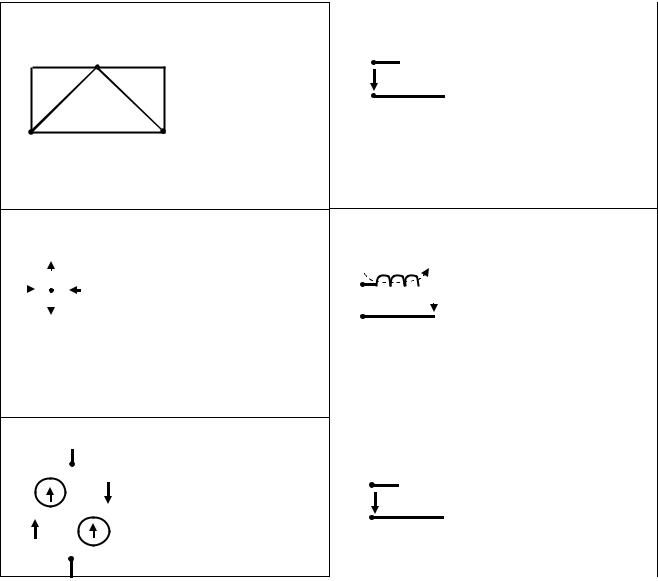
В нашем примере на участке от 0 до T/2 кривая тока представляет собой прямую, проходящую через начало координат под острым углом 1 90 к оси
t, и поэтому производная di / dt на этом участке есть постоянная и положительная конечная величина.
На участке от T/2 до Т ток представляет собой прямую, составляющую тупой угол с осью t 2 90 , и поэтому производная di / dt на этом участке есть постоянная и отрицательная величина. При этом tg 2 tg (180 1 ) tg 1 .
Таким образом, график искомого напряжения представляет собой отрезки прямых, меняющих каждую половину периода свой знак, как это показано на рис. 1.7,б.
Вопросы для самопроверки
1) Дана структурная схема цепи. Сколько ветвей в данной цепи?
2) Найдите правильное уравнение:
1. i1 i2 i3 i4 0 | ||||||||
i4 | i1 | i2 | ||||||
2. i i | i | i 0 | ||||||
1 | 2 | 3 | 4 | |||||
i3 | 3. i1 i2 i3 i4 0 | |||||||
4.i1 i2 i3 i4 0
5.i1 i2 i3 i4 0
3)Выберите правильное уравнение:
1. e1 e2 u1 u2 | ||
e1 | u2 | |
2. e1 e2 u1 u2 | ||
u1 | e2 | 3. e1 e2 u1 u2 |
4. e1 e2 u1 u2 | ||
6)Дано: С = 1000 мкФ; U = 100 В.
С | |||||
U | Определите заряд | ||||
конденсатора q Кл. | |||||
0,1 | 0,2 | 0,3 | 0,4 | 0,5 |
1. | 2. | 3. | 4. | 5. |
7)Дано: L =10 мГн; I = 100 A.
L | Определите | ||||
I | потокосцепление | ||||
катушки | Вб. | ||||
4 | 3 | 2 | 1 | 0,5 | |
1. | 2. | 3. | 4. | 5. | |
8)Дано: WЭ = 0,05 Дж; С = 10 мкФ.
С | Определите напряжение | |||
U | на конденсаторе U В. | |||
43
Источник
Электромагнитные процессы, протекающие
в электротехнических устройствах, как правило, достаточно сложны. Однако во
многих случаях, их основные характеристики можно описать с помощью таких интегральных
понятий, как: напряжение, ток, электродвижущая сила (ЭДС). При таком подходе
совокупность электротехнических устройств, состоящую из соответствующим образом
соединенных источников и приемников электрической энергии, предназначенных для
генерации, передачи, распределения и преобразования электрической энергии и
(или) информации, рассматривают как электрическую цепь. Электрическая
цепь состоит из отдельных частей (объектов), выполняющих определенные функции
и называемых элементами цепи. Основными элементами цепи являются источники
и приемники электрической энергии (сигналов). Электротехнические устройства,
производящие электрическую энергию, называются генераторами или источниками
электрической энергии, а устройства, потребляющие ее – приемниками
(потребителями) электрической энергии.
У каждого элемента цепи можно выделить
определенное число зажимов (полюсов), с помощью которых он соединяется
с другими элементами. Различают двух –и многополюсные элементы.
Двухполюсники имеют два зажима. К ним относятся источники энергии (за исключением
управляемых и многофазных), резисторы, катушки индуктивности, конденсаторы.
Многополюсные элементы – это, например, триоды, трансформаторы, усилители и
т.д.
Все элементы электрической цепи условно
можно разделить на активные и пассивные. Активным называется элемент,
содержащий в своей структуре источник электрической энергии. К пассивным относятся
элементы, в которых рассеивается (резисторы) или накапливается (катушка индуктивности
и конденсаторы) энергия. К основным характеристикам элементов цепи относятся
их вольт-амперные, вебер-амперные и кулон-вольтные характеристики, описываемые
дифференциальными или (и) алгебраическими уравнениями. Если элементы описываются
линейными дифференциальными или алгебраическими уравнениями, то они называются
линейными, в противном случае они относятся к классу нелинейных.
Строго говоря, все элементы являются нелинейными. Возможность рассмотрения их
как линейных, что существенно упрощает математическое описание и анализ процессов,
определяется границами изменения характеризующих их переменных и их частот.
Коэффициенты, связывающие переменные, их производные и интегралы в этих уравнениях,
называются параметрами элемента.
Если параметры элемента не являются функциями
пространственных координат, определяющих его геометрические размеры, то он называется
элементом с сосредоточенными параметрами. Если элемент описывается уравнениями,
в которые входят пространственные переменные, то он относится к классу элементов
с распределенными параметрами. Классическим примером последних является
линия передачи электроэнергии (длинная линия).
Цепи, содержащие только линейные элементы,
называются линейными. Наличие в схеме хотя бы одного нелинейного элемента относит
ее к классу нелинейных.
Рассмотрим пассивные элементы цепи, их
основные характеристики и параметры.
1. Резистивный элемент (резистор)
Условное графическое изображение резистора приведено на рис. 1,а. Резистор
– это пассивный элемент, характеризующийся резистивным сопротивлением. Последнее
определяется геометрическими размерами тела и свойствами материала: удельным
сопротивлением r (Ом´
м) или обратной величиной – удельной проводимостью
(См/м).
В простейшем случае проводника длиной
и сечением S его сопротивление определяется выражением
.
В общем случае
определение сопротивления связано с расчетом поля в проводящей среде, разделяющей
два электрода.
Основной характеристикой резистивного элемента является зависимость
(или ),
называемая вольт-амперной характеристикой (ВАХ). Если зависимость
представляет собой прямую линию, проходящую через начало координат (см.рис.
1,б), то резистор называется линейным и описывается соотношением
или
,
где –
проводимость. При этом R=const.
Нелинейный резистивный элемент, ВАХ которого нелинейна (рис. 1,б), как будет
показано в блоке лекций, посвященных нелинейным цепям, характеризуется несколькими
параметрами. В частности безынерционному резистору ставятся в соответствие статическое
и дифференциальное
сопротивления.
2. Индуктивный элемент (катушка индуктивности)
Условное графическое изображение катушки индуктивности приведено на рис. 2,а.
Катушка – это пассивный элемент, характеризующийся индуктивностью. Для расчета
индуктивности катушки необходимо рассчитать созданное ею магнитное поле.
Индуктивность определяется отношением потокосцепления к току, протекающему
по виткам катушки,
.
В свою очередь потокосцепление равно сумме произведений потока, пронизывающего
витки, на число этих витков ,
где .
Основной характеристикой катушки индуктивности является зависимость ,
называемая вебер-амперной характеристикой. Для линейных катушек индуктивности
зависимость
представляет собой прямую линию, проходящую через начало координат (см. рис.
2,б); при этом
.
Нелинейные свойства катушки индуктивности (см. кривую
на рис. 2,б) определяет наличие у нее сердечника из ферромагнитного материала,
для которого зависимость
магнитной индукции от напряженности поля нелинейна. Без учета явления магнитного
гистерезиса нелинейная катушка характеризуется статической
и дифференциальной
индуктивностями.
3. Емкостный элемент (конденсатор)
Условное графическое изображение конденсатора приведено на рис. 3,а.
Конденсатор – это пассивный элемент, характеризующийся емкостью. Для расчета
последней необходимо рассчитать электрическое поле в конденсаторе. Емкость определяется
отношением заряда q на обкладках конденсатора к напряжению u между ними
и зависит от геометрии обкладок и свойств диэлектрика, находящегося между ними.
Большинство диэлектриков, используемых на практике, линейны, т.е. у них относительная
диэлектрическая проницаемость
=const. В этом случае зависимость
представляет собой прямую линию, проходящую через начало координат, (см. рис.
3,б) и
.
У нелинейных диэлектриков (сегнетоэлектриков) диэлектрическая проницаемость
является функцией напряженности поля, что обусловливает нелинейность зависимости
(рис.
3,б). В этом случае без учета явления электрического гистерезиса нелинейный
конденсатор характеризуется статической
и дифференциальной
емкостями.
Схемы замещения источников электрической энергии
Свойства источника электрической энергии описываются ВАХ ,
называемой внешней характеристикой источника. Далее в этом разделе для
упрощения анализа и математического описания будут рассматриваться источники
постоянного напряжения (тока). Однако все полученные при этом закономерности,
понятия и эквивалентные схемы в полной мере распространяются на источники переменного
тока. ВАХ источника может быть определена экспериментально на основе схемы,
представленной на рис. 4,а. Здесь вольтметр V измеряет напряжение на зажимах
1-2 источника И, а амперметр А – потребляемый от него ток I, величина которого
может изменяться с помощью переменного нагрузочного резистора (реостата) RН.
В общем случае ВАХ источника является нелинейной (кривая 1 на рис. 4,б). Она
имеет две характерные точки, которые соответствуют:
а – режиму холостого хода ;
б – режиму короткого замыкания .
Для большинства источников режим короткого замыкания (иногда холостого хода)
является недопустимым. Токи и напряжения источника обычно могут изменяться в
определенных пределах, ограниченных сверху значениями, соответствующими номинальному
режиму (режиму, при котором изготовитель гарантирует наилучшие условия его
эксплуатации в отношении экономичности и долговечности срока службы). Это позволяет
в ряде случаев для упрощения расчетов аппроксимировать нелинейную ВАХ на рабочем
участке m-n (см. рис. 4,б) прямой, положение которой определяется рабочими интервалами
изменения напряжения и тока. Следует отметить, что многие источники (гальванические
элементы, аккумуляторы) имеют линейные ВАХ.
Прямая 2 на рис. 4,б описывается линейным уравнением
| , | (1) |
где – напряжение на зажимах
источника при отключенной нагрузке (разомкнутом ключе К в схеме на рис. 4,а);
– внутреннее
сопротивление источника.
Уравнение (1) позволяет составить последовательную схему замещения
источника (см. рис. 5,а). На этой схеме символом Е обозначен элемент, называемый
идеальным источником ЭДС. Напряжение на зажимах этого элемента
не зависит от тока источника, следовательно, ему соответствует ВАХ на рис. 5,б.
На основании (1) у такого источника .
Отметим, что направления ЭДС и напряжения на зажимах источника противоположны.
Если ВАХ источника линейна, то для определения параметров
его схемы замещения необходимо провести замеры напряжения и тока для двух
любых режимов его работы.
Существует также параллельная схема замещения источника. Для ее описания разделим
левую и правую части соотношения (1) на .
В результате получим
или
| , | (2) |
где ;
– внутренняя
проводимость источника.
Уравнению (2) соответствует схема замещения источника на рис. 6,а.
На этой схеме символом J обозначен элемент, называемый идеальным источником
тока. Ток в ветви с этим элементом равен
и не зависит от напряжения на зажимах источника, следовательно, ему соответствует
ВАХ на рис. 6,б. На этом основании с учетом (2) у такого источника ,
т.е. его внутреннее сопротивление .
Отметим, что в расчетном плане при выполнении условия
последовательная и параллельная схемы замещения источника являются эквивалентными.
Однако в энергетическом отношении они различны, поскольку в режиме холостого
хода для последовательной схемы замещения мощность равна нулю, а для параллельной
– нет.
Кроме отмеченных режимов функционирования источника, на практике важное значение
имеет согласованный режим работы, при котором нагрузкой RН от источника
потребляется максимальная мощность
| , | (3) |
Условие такого режима
| , | (4) |
В заключение отметим, что в соответствии с ВАХ на рис. 5,б и 6,б идеальные
источники ЭДС и тока являются источниками бесконечно большой мощности.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия, 1972. –240 с. - Каплянский А.Е. и др. Теоретические основы электротехники. Изд. 2-е.
Учеб. пособие для электротехнических и энергетических специальностей вузов.
–М.: Высш. шк., 1972. –448 с.
Контрольные вопросы и задачи
- Может ли внешняя характеристик источника проходить через начало координат?
- Какой режим (холостой ход или короткое замыкание) является аварийным для
источника тока? - В чем заключаются эквивалентность и различие последовательной и параллельной
схем замещения источника? - Определить индуктивность L и энергию магнитного поля WМкатушки, если при
токе в ней I=20А потокосцепление y =2 Вб.Ответ: L=0,1 Гн; WМ=40 Дж.
- Определить емкость С и энергию электрического поля WЭконденсатора, если
при напряжении на его обкладках U=400 В заряд конденсатора q=0,2´
10-3 Кл.Ответ: С=0,5 мкФ; WЭ=0,04 Дж.
- У генератора постоянного тока при токе в нагрузке I1=50Анапряжение на зажимах
U1=210 В,а притоке, равном I2=100А, оно снижается до U2=190 В. - Определить параметры последовательной схемы замещения источника и ток короткого
замыкания.Ответ:
- Вывести соотношения (3) и (4) и определить максимальную мощность, отдаваемую
нагрузке, по условиям предыдущей задачи.Ответ:
Источник
