Какие свойства используют в пропорции

Что такое пропорция
Определение пропорции:
Пропорция — это равенство двух отношения.
Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.
Пропорция всегда содержит равные коэффициенты.
Если выразить определение формулой, то выглядеть оно будет так:
- a : b = c : d
Или вот так:
a и d — крайние члены пропорции
Читается это выражение так: a так относится к b, как c относится к d
Например:
15 : 5 = 3
9 : 3 = 3
Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.
15 и 3 — крайние члены пропорции.
5 и 9 — средние члены пропорции.
Наглядный пример для понимания:
У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.
- Запишем эту непростую ситуацию в виде отношения 8 кусочков к 4 голодным друзьям: 8 : 4
- Далее преобразовываем это отношение в дробь: 8/4
- Выполняем деление: 8/4 = 2
Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!
А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.
Что мы имеем: 4 кусочка и 2 друга, претендующих на них.
- Запишем в виде отношения: 4 : 2
- Преобразовываем получившееся отношение в дробь: 4/2
- Выполняем деление: 4/2 = 2
Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.
Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.
Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным????
Чтобы ребенок понимал, как еще использовать математику в обычной жизни, запишите его на бесплатный вводный урок в онлайн-школу Skysmart.
Ученики занимаются в интерактивном формате, помогают героям комиксов справиться с коварными задачками, отслеживают прогресс в личном кабинете и не боятся школьных контрольных.
Основное свойство пропорции
Запомните основное свойство пропорции:
Произведение крайних членов пропорции равно произведению средних членов этой пропорции.
В виде формулы свойство выглядит так:
a : b = c : d = a * d = b * c
Мы знаем, что a и d — крайние члены пропорции, b и c — средние.
Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.
Давайте проверим несколько пропорций.
Пример 1. Дана пропорция:6/2 = 12/4
- Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
- Далее перемножаем средние члены пропорции: 2 * 12 = 24
- Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
- 6 * 4 = 2 * 12
24 = 24
Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.
Пример 2. Дана пропорция: 10/2 = 16/4
- Перемножаем крайние члены пропорции: 10 * 4 = 40.
- Перемножаем средние члены: 16 * 2 = 32.
- Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32.
- 10 * 4 ≠ 16 * 2
40 ≠ 32
Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.
Примеры решения задач
Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.
Задачка 1. Дана математическая пропорция: 15/3 = x/4
Найдите x.
Как решаем:
- По основному свойству пропорции перемножаем множители:
15 * 4 = 3x - Получаем уравнение: 60 = 3x
- 60/3 = x
x = 20.
Ответ: в пропорции 15/3 = x/4, x = 20
Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.
Как решаем:
- Записываем чиcла в виде дробей: 18/9 = 24/x
Где x — четвертый член пропорции. - По основному свойству пропорции, перемножаем средние члены: 9 * 24 = 216
- Выводим уравнение 18x = 216
- Находим x:
x = 216 : 18
x = 12 - Проверяем: 9 * 24 = 216, 18 * 12 = 216.
Пропорция составлена верно.
Ответ: четвертый член пропорции — 12.
Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?
Как решаем:
- Записываем числа в виде дроби: 18/9 = x/8
- Перемножаем множители по основному свойству пропорции: 18 * 8 = 9x
- Находим х:
144 = 9x
144 : 9 = 16
Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.
Задачка 4. Дана пропорция: 20/2 = y/4
Найдите y.
Как решаем:
- По основному свойству пропорции перемножаем множители:
20 * 4 = 2y - Получаем уравнение: 80 = 2y
- Находим у:
80/2 = y
x = 40. - Проверяем пропорцию: 20 * 4 = 80, 40 * 2 = 80.
Ответ: в пропорции 20/2 = y/4, y = 40
Есть одна проверенная пропорция, которая выглядит вот так: математика так относится к ученику, как ученик относится к математике — полное равенство отношений.
Чтобы ваш ребенок выстроил добрые пропорциональные отношения с математикой, записывайтесь на бесплатный вводный урок в онлайн-школу Skysmart. Наши преподаватели объяснят самые сложные темы и научат ребенка получать настоящее удовольствие от решения задачек.
Источник
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение равно отношению
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Дроби, из которых составлена пропорция, всегда равны. Например, если в пропорции выполнить деление в обеих дробях, то получится число 2 в обеих частях:
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение пропорционально отношению . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение не пропорционально отношению .
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями и знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции крайние члены это 4 и 4, а средние члены это 2 и 8
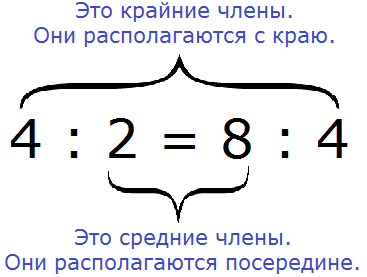
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
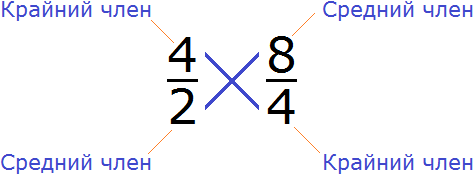
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
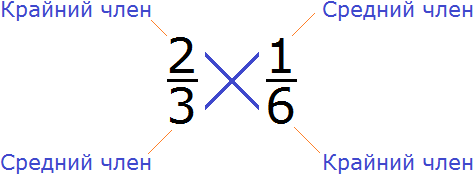
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция составлена неправильно.
Поэтому в пропорции разумнее заменить знак равенства (=) на знак не равно (≠)
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Источник
Здравствуйте, уважаемые читатели! Сегодня хочу с Вами поговорить на такую замечательную тему, как пропорции. Понятия “пропорция, пропорционально” повсеместно используются не только в математике, но и в повседневной жизни. Сначала предлагаю посмотреть на пропорции с математической точки зрения, затем с точки зрения практического применения.
Пропорция
Итак, давайте вспомним, что же такое пропорция? Почему вспомним? – спросите Вы – все и так знают, что это такое. Да, знают и понимают это практически все, но кто сможет сходу дать ей определение? )) В самом широком смысле, пропорция – это равенство соотношений. С точки зрения математики, соотношение может быть арифметическим или геометрическим. Например числа 5, 3 и 6, 4 составляют арифметическую пропорцию, так как разность между 5 и 3 равна разности между 6 и 4. А числа 18, 3 и 24, 4 находятся в пропорции геометрической, потому что отношение 18 к 3 равно отношению 24 к 4. Это как разница между арифметической и геометрической прогрессиями. Есть ещё и пропорция, которая называется гармонической. В отличии от двух предыдущих, в ней участвуют не четыре, а два числа. Но они относятся друг к другу по правилу золотого сечения, о котором я уже писал. Двумя целыми числами, составляющими гармоническую пропорцию, могут быть достаточно большие члены ряда Фибоначчи, например, 987 и 610, так как 987/610=(987+610)/987=1,61803=Ф (с точностью до 5-го знака).
Более пристальное внимание в школьном курсе математики уделяется геометрическим пропорциям, так как у арифметических особых свойств нет, кроме того, что это просто равенство двух разностей. А поскольку о золотом сечении, как говорилось выше, я уже достаточно подробно писал, то далее речь пойдёт о свойствах геометрической пропорции. Дальше для краткости я буду писать просто пропорция, имея ввиду именно геометрическую.
Вспомним, что в пропорции a/b=c/d числа a и d называют крайними членами, b и c – средними членами пропорции. Первое свойство пропорции – это сохранение равенства при перемножении крайних и средних членов:
Свойство пропорции
Второе, на мой взгляд, самое важное, свойство пропорции – это то, что при перемене местами крайних членов, так же как и средних, равенство пропорции сохраняется:
Свойства пропорции
Как видно из этих свойств также следует, что равенство сохраняется и при перемене местами числителей и знаменателей. Честно признаюсь, меня это до сих пор завораживает! ))
Есть также свойство увеличения и уменьшения пропорции:
Свойство пропорции
Но и это ещё не всё! Есть также свойство составления пропорции сложением и вычитанием:
Свойство пропорции
По-моему, это просто поразительно! Четыре числа – и столько равенств!
Теперь о практике. Использование в жизни пропорций настолько велико, что примеры можно перечислять бесконечно. Это, в первую очередь, архитектура; а так же искусство: живопись, скульптура, музыка, и т. д. Применяют пропорции, конечно же, и в самых различных вычислениях. Вспомните мой пример из статьи о подобных треугольниках. Если ещё не читали, обязательно прочитайте. По-моему, свойства пропорций имеют огромное значение в нашей жизни. Часто мы об этом даже не догадываемся ))
Надеюсь, Вам было интересно. Спасибо, что прочитали!
Чтобы не пропустить новых интересных статей о математике, предлагаю Вам подписаться на мой канал.
P.S. Ответ на задачку о гусях из прошлой статьи. Правильное число: 36.
Предыдущая статья
Следующая статья
Источник
Пропорции
Мы достаточно часто в жизни сталкиваемся с понятием «пропорция». Это и пропорция предмета, и пропорция в каком-нибудь кулинарном рецепте, и пропорции в искусстве. Только далеко не все понимают, что это такое. Разберёмся.
Пропорцией называется равенство двух отношений.
То есть, при делении а на b получается такое же число, как и при делении cна d.
Пример 1. Отношение числа 28 к числу 7 равно 4; отношение числа 64 к числу 16 тоже равно 4, значит, является верной пропорцией.
Два числа, которые мы пишем первым и последним, называются крайними членами пропорции; а два числа, которые мы пишем в середине, называются среднимичленами пропорции.
В нашей формуле aиd– крайние члены, а bи c– средние члены.
У пропорции есть замечательное свойство.
Основное свойство пропорции:
Пропорция верна тогда и только тогда, когда произведение её крайних членов равно произведению её средних членов.
Пример 2. Проверить, является ли пропорция верной.
Произведение крайних членов равно:
Произведение средних членов равно:
Эти два произведения равны, значит, данная пропорция верна.
Есть ещё одно свойство пропорции:
Если в верной пропорции поменять местами крайние (или средние) члены, то получившаяся пропорция тоже будет верна.
Пример 3. Пропорция верна. Значит, будут верны и такие пропорции:
Используя основное свойство пропорции, можно задать алгоритм нахождения неизвестного члена пропорции.
Чтобы найти неизвестный крайний член пропорции, нужно перемножить средние члены и разделить на известный крайний член.
Чтобы найти неизвестный средний член пропорции, нужно перемножить крайние члены и разделить на известный средний член.
Пример 4. Найти неизвестный член пропорции:
Ответ: 35
Из чисел 16; 6; 8; 12 составить верную пропорцию.
Из чисел 2,4; 4,2; 7,2; 12,6 составить верную пропорцию.
Из чисел 1,5; 4,9; 2,1; 3,5 составить верную пропорцию.
Из чисел 2,3; 9,3; 3,1; 6,9 составить верную пропорцию.
Верна ли пропорция ?
Верна ли пропорция ?
Верна ли пропорция ?
Верна ли пропорция ?
Решить уравнение:
Масса 15 одинаковых деталей составила 37,5 кг. Какова масса 12 таких деталей?
До обеда скосили 2,8 га, что составляет 24% площади луга. После обеда скосили ещё 2,1 га. Сколько процентов луга скосили за день?
Когда цех выпустил 360 приборов, то он выполнил 120% месячной нормы. Какова месячная норма?
Самолёт пролетел расстояние между двумя аэродромами за 6 ч со скоростью 850 км/ч. За сколько времени пролетит это расстояние другой самолёт, скорость которого на 150 км/ч больше скорости первого?
На 20 км пути автомобиль расходует л горючего. Сколько горючего израсходует этот же автомобиль на 50 км пути?
Для отопления здания заготовлено угля на 180 дней при норме расхода 0,6 т угля в день. На сколько дней хватит этого запаса, если его расходовать ежедневно по 0,5 т?
Краеобмёточная машина 0,6 м ткани обработает за 2,16 мин. Сколько потребуется времени, чтобы обметать 1,25 м такой ткани? Сколько метров можно обметать за 1,44 мин?
Распилили 3,2 м3 дров, что составляет 22,4% привезённых дров. Сколько ещё надо распилить дров, чтобы они составляли 33,6% привезённых дров?
Когда изготовили 756 деталей, то выполнили план на 72%. Сколько деталей должны изготовить по плану?
Теплоход на подводных крыльях прошёл расстояние между двумя пристанями со средней скоростью 60 км/ч за 2,5 ч. За сколько времени пройдёт это расстояние теплоход, если будет идти со скоростью 50 км/ч?
На изготовление 8 деталей требуется г серебра. Сколько серебра потребуется на изготовление 12 таких деталей?
24 человека за 6 дней пропололи участок клубники. За сколько дней выполнят ту же работу 36 человек, если будут работать с той же производительностью?
0,7 кг печенья автомат расфасовывает за 2,03 мин. За сколько минут этот автомат расфасует 1,5 кг печенья? Сколько печенья он может расфасовать за 1,16 минут?
Расфасовали 0,9 т крупы, что составляет 46,8% всей крупы, привезённой в магазин. Сколько крупы надо ещё расфасовать, чтобы она составляла 65% привезённой крупы?
Когда израсходовали 78,4 кг картофеля, то оказалось, что израсходовано 24,5% всего запаса. Сколько кг картофеля было запасено?
Теплоход «Ракета» прошёл расстояние между пристанями со скоростью 50 км/ч за 4,8 ч. С какой скоростью должен идти теплоход, чтобы пройти это расстояние за 3,2 ч?
На изготовление 14 деталей расходуется 16,8 кг металла. Сколько потребуется металла на изготовление 27 таких деталей?
На участке дороги бетонные плиты длиной 6 м заменили новыми длиной 8 м. Сколько нужно новых плит для замены 240 старых?
За 0,7 кг заплатили 280 рублей. Сколько надо заплатить за 1,9 кг такого мяса? Сколько мяса можно купить на 420 рублей?
Рассортировали 13,6 т зерна, что составило 54% имевшегося зерна. Сколько тонн зерна надо ещё рассортировать, чтобы осталось лишь 19% имевшего зерна?
Когда сдали на элеватор 2,1 тыс. т пшеницы, то оказалось, что план сдачи зерна выполнен на 105%. Сколько тонн зерна надо было сдать по плану?
Всадник, двигаясь со скоростью 18 км/ч, преодолел некоторое расстояние за 1,5 ч. За какое время проедет это расстояние экипаж, скорость которого на 3 км/ч меньше скорости всадника?
Для изготовления 10 деталей требуется кг металла. Сколько металла пойдёт на изготовление 12 таких деталей?
Для перевозки груза автомобилю, грузоподъёмностью 6 т надо сделать 10 рейсов. Сколько придётся сделать рейсов автомобилю, грузоподъёмность которого на 2 т меньше, чтобы перевезти этот груз?
4
Источник
