Какие свойства имеют графы
1. Методические рекомендации к теме
“Графы”.
Понятие графа целесообразно вводить после
того, как разобрано несколько задач, подобных
задаче 1, решающее соображение в которых –
графическое представление. Важно, чтобы ученики
сразу осознали, что один и тот же граф может быть
нарисован разными способами. Строгое
определение графа, на мой взгляд, давать не нужно,
т.к. оно слишком громоздко и это только затруднит
обсуждение. На первых порах хватит и
интуитивного понятия. При обсуждении понятия
изоморфизма можно решить несколько упражнений
на определение изоморфных и неизоморфных графов.
Одно из центральных мест темы – теорема о
четности числа нечетных вершин. Важно, чтобы
ученики до конца разобрались в ее доказательстве
и научились применять к решению задач. При
разборе нескольких задач рекомендую не
ссылаться на теорему, а фактически повторять ее
доказательство. Чрезвычайно важно также понятие
связности графа. Содержательным соображением
здесь является рассмотрение компоненты
связности, на это необходимо обратить особое
внимание. Эйлеровы графы – тема почти игровая.
Первая и главная цель, которую нужно
преследовать при изучении графов, –научить
школьников видеть граф в условии задачи и
грамотно переводить условие на язык теории
графов. Не стоят рассказывать обе всем на
нескольких занятиях подряд. Лучше разнести
занятия по времени на 2–3 учебных года. (Прилагается
разработка занятия “Понятие графа. Применение
графов к решению задач” в 6 классе).
2. Теоретический материал к теме
“Графы”.
Введение
Графы – замечательные математические объекты,
с их помощью можно решать очень много различных,
внешне не похожих друг на друга задач. В
математике существует целый раздел – теория
графов, который изучает графы, их свойства и
применение. Мы же обсудим только самые основные
понятия, свойства графов и некоторые способы
решения задач.
Понятие графа
Рассмотрим две задачи.
Задача 1. Между девятью планетами
солнечной системы установлено космическое
сообщение. Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты
изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до
Марса нельзя.
Задача 2. Доска имеет форму двойного
креста, который получается, если из квадрата 4×4
убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и
вернуться на исходную клетку, побывав на всех
клетках ровно по одному разу ?
Решение: Занумеруем последовательно
клетки доски:
А теперь с помощью рисунка покажем, что такой
обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако
решения этих двух задач объединяет общая идея –
графическое представление решения. При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
Такие картинки и называются графами. Точки
при этом называются вершинами, а линии – ребрами
графа. Заметим, что не каждая картинка такого
вида будет называться графом. Например. если вас
попросят нарисовать в тетради пятиугольник, то
такой рисунок графом не будет. Будем называть что
рисунок такого вида, как в предыдущих задачах,
графом, если есть какая-то конкретная задача для
которой такой рисунок построен.
Другое замечание касается вида графа.
Попробуйте проверить, что граф для одной и той же
задачи можно нарисовать разными способами; и
наоборот для разных задач можно нарисовать
одинаковые по виду графы. Здесь важно лишь то,
какие вершины соединены друг с другом, а какие –
нет. Например, граф для задачи 1 можно нарисовать
по-другому:
Такие одинаковые, но по-разному нарисованные
графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины
графа называется количество выходящих из нее
ребер. В связи с этим, вершина, имеющая четную
степень, называется четной вершиной,
соответственно, вершина, имеющая нечетную
степень, называется нечетной вершиной.
С понятием степени вершины связана одна из
основных теорем теории графов –теорема о
честности числа нечетных вершин. Докажем ее мы
немного позднее, а сначала для иллюстрации
рассмотрим задачу.
Задача 3. В городе Маленьком 15
телефонов. Можно ли их соединить проводами так,
чтобы каждый телефон был соединен ровно с пятью
другими ?
Решение: Допустим, что такое соединение
телефонов возможно. Тогда представим себе граф, в
котором вершины обозначают телефоны, а ребра –
провода, их соединяющие. Подсчитаем, сколько
всего получится проводов. К каждому телефону
подключено ровно 5 проводов, т.е. степень каждой
вершины нашего графа – 5. Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.
Ответ. Соединить телефоны таким образом
невозможно.
Теорема: Любой граф содержит четное
число нечетных вершин.
Доказательство: Количество ребер графа
равно половине суммы степеней его вершин. Так как
количество ребер должно быть целым числом, то
сумма степеней вершин должна быть четной. А это
возможно только в том случае, если граф содержит
четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к
графам – понятие связности.
Граф называется связным, если из любые две
его вершины можно соединить путем, т.е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов,
каждый из городов соединен дорогами не менее, чем
с семью другими. Докажите, что из каждого города
модно добраться в любой другой.
Доказательство: Рассмотрим два
произвольных А и В города и допустим, что между
ними нет пути. Каждый из них соединен дорогами не
менее, чем с семью другими, причем нет такого
города, который был бы соединен с обоими
рассматриваемыми городами (в противном случае
существовал бы путь из A в B). Нарисуем часть графа,
соответствующую этим городам:
Теперь явно видно, что мы получили не менее
различных 16 городов, что противоречит условию
задачи. Значит утверждение доказано от
противного.
Если принять во внимание предыдущее
определение, то утверждение задачи можно
переформулировать и по-другому: “Доказать, что
граф дорог страны Семерка связен.”
Теперь вы знаете, как выглядит связный граф.
Несвязный граф имеет вид нескольких “кусков”,
каждый из которых – либо отдельная вершина без
ребер, либо связный граф. Пример несвязного графа
вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой
связности графа. Каждая компонента связности
представляет собой связный граф и для нее
выполняются все утверждения, которые мы доказали
для связных графов. Рассмотрим пример задачи, в
которой используется компонента связности:
Задача 5. В Тридевятом царстве только
один вид транспорта – ковер-самолет. Из столицы
выходит 21 ковролиния, из города Дальний – одна, а
из всех остальных городов, – по 20. Докажите, что
из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если
нарисовать граф ковролиний Царства, то он может
быть несвязным. Рассмотрим компоненту связности,
которая включает в себя столицу Царства. Из
столицы выходит 21 ковролиния, а из любых других
городов, кроме города Дальний – по 20, поэтому,
чтобы выполнялся закон о четном числе нечетных
вершин необходимо, чтобы и город Дальний входил в
эту же самую компоненту связности. А так как
компонента связности – связный граф, то из
столицы существует путь по ковролиниям до города
Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых
требуется нарисовать какую-либо фигуру не
отрывая карандаш от бумаги и проводя каждую
линию только один раз. Оказывается, что такая
задача не всегда разрешима, т.е. существуют
фигуры, которые указанным способом нарисовать
нельзя. Вопрос разрешимости таких задач также
входит в теорию графов. Впервые его исследовал в
1736 году великий немецкий математик Леонард
Эйлер, решая задачу о Кенигсбергских мостах.
Поэтому графы, которые можно нарисовать
указанным способом, называются Эйлеровыми
графами.
Задача 6. Можно ли нарисовать
изображенный на рисунке граф не отрывая карандаш
от бумаги и проводя каждое ребро ровно один раз ?
Решение. Если мы будем рисовать граф так,
как сказано в условии, то в каждую вершину, кроме
начальной и конечной, мы войдем столько же раз,
сколько выйдем из нее. То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не
более двух нечетных вершин.
И в заключение – задача о Кенигсбергских
мостах.
Задача 7. На рисунке изображена схема
мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти
по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так,
как показано на рис.1. Можно ли сделав несколько
ходов конями, переставить их в положение,
показанное на рис.2?
Рис. 1 | Рис. 2 |
Решение. Занумеруем клетки доски, как
показано на рисунке:
Каждой клетке поставим в соответствие точку на
плоскости и, если из одной клетки можно попасть в
другую ходом шахматного коня, то соответствующие
точки соединим линией. Исходная и требуемая
расстановки коней показаны на рисунках:
При любой последовательности ходов конями
порядок их следования, очевидно, измениться не
может. Поэтому переставить коней требуемым
образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2,
3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два
города соединены авиалинией в том и только в том
случае, если двузначное число, образованное
названиями городов, делится на 3. Можно ли
долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому
городу точку и соединив точки линией, если сумма
цифр делится на 3, получим граф, в котором цифры 3,
5, 9 связаны между собой, но не связаны с
остальными. Значит долететь из города 1 в город 9
нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города
выходит 4 дороги. Сколько всего дорог в
государстве.
Решение. Подсчитаем общее количество
выходящих городов дорог – 100 . 4 =
400. Однако при таком подсчете каждая дорога
посчитана 2 раза – она выходит из одного города и
входит в другой. Значит всего дорог в два раза
меньше, т.е. 200.
4. В классе 30 человек. Может ли быть так, что 9
человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5
друзей ?
Ответ. Нет (теорема о четности числа
нечетных вершин).
5. У короля 19 вассалов. Может ли оказаться так,
что у каждого вассала 1, 5 или 9 соседей ?
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого
города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число
дорог равно числу городов х, умноженному на 3
(число выходящих из каждого города дорог) и
разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо
на Земле и сделавших нечетное число рукопожатий,
четно.
Доказательство непосредственно следует из
теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и
из каждого города можно добраться до любого
другого. Одну дорогу закрыли на ремонт. Докажите,
что и теперь из любого города можно добраться до
любого другого.
Доказательство. Рассмотрим компоненту
связности, в которую входит один из городов,
дорогу между которыми закрыли. По теореме о
четности числа нечетных вершин в нее входит и
второй город. А значит по-прежнему можно найти
маршрут и добраться из одного из этих городов в
другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами
так, что от каждого острова можно добраться до
любого другого. Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на
несколько частей заборами. Можно ли прогуляться
по парку и его окрестностям так, чтобы перелезть
через каждый забор розно 1 раз?
Источник
Определение 17.2. Путь (path) в графе -это последовательность вершин, в которой каждая следующая вершина (после первой), является смежной с предыдущей вершиной на этом пути. Простой путь (simple path) -это путь, все вершины и ребра, составляющие, различны. Циклом (cycle) называется путь, у которого первая и последняя вершина одна и та же.
Иногда используется термин циклический путь (cyclic path) -для обозначения пути, у которого совпадают первая и последняя вершина (но который в других отношениях не обязательно является простым); а термин контур (tour) употребляется для циклического пути, который включает каждую вершину. Путь можно определить и как последовательность ребер, которая соединяет соседние вершины. Мы подчеркиваем это в наших обозначениях, соединяя имена вершин в пути так же, как и в обозначениях ребер. Например, на
рис.
17.1 имеются простые пути 3-4-6-0-2 и 9-11-12 и циклы 0-6-4-3-5-0 и 5-4-3-5. Длина (length) пути или цикла определяется как количество составляющих их ребер.
Мы будем считать, что каждая отдельная вершина представляет собой путь длины 0 (путь из некоторой вершины в ту же вершину, не содержащий ребер, отличных от петли на себя). Кроме этого, будем считать, что в графе, не содержащем параллельных ребер и петель, любая пара вершин однозначно определяет некоторое ребро, пути должны состоять по меньшей мере из двух различных вершин, а циклы должны содержать не менее трех различных ребер и трех различных вершин.
Два простых пути называются непересекающимися (disjoint), если они не содержат общих вершин, кроме, возможно, концевых. Это условие несколько слабее, чем требование полного отсутствия в обоих путях общих вершин, и оно более полезно, поскольку в этом случае мы можем соединить простые непересекающиеся пути из s в t и из t в u и получить простой непересекающийся путь из s в u, если вершины s и u различны (и получить цикл, если s и u совпадают). Иногда используется термин непересекающиеся по вершинам (vertex disjoint), чтобы отличить эту ситуацию от более сильного условия непе-ресекающихся по ребрам (edge disjoint) путей, когда пути не должны иметь общих ребер.
Определение 17.3. Граф называется связным графом (connected graph), если существует путь из каждой вершины в любую другую вершину графа. Не связный граф состоит из некоторого множества связных компонентов, которые представляют собой максимальные связные подграфы.
Термин максимальный связный подграф (maximal connected subgraph) означает, что не существует пути из вершины такого подграфа в любую другую вершину графа, который не содержался бы в этом подграфе. Если бы вершины были физическими объектами, как, скажем, узлы или бусинки, а ребра были бы физическими соединениями, такими как, например, нити или провода, то связный граф останется целым, если потянуть за любую его вершину, а несвязный граф распадется на две или больше частей.
Определение 17.4. Ациклический связный граф называется деревом (tree) (см.
“Рекурсия и деревья”
). (Ациклическим называется граф, в котором отсутствуют циклы -прим. перев.) Множество деревьев называется лесом (forest) или бором. Остовное дерево (spanning tree) связного графа -это подграф, который содержит все вершины этого графа и представляет собой единое дерево. Остовный лес (spanning forest) графа -это лес, который содержит все вершины этого графа.
Например, граф на
рис.
17.1 с тремя связными компонентами может иметь остовный лес 7-8 9-10 9-11 9-12 0-1 0-2 0-5 5-3 5-4 4-6 (существует и множество других остовных лесов). На
рис.
17.3 эти и некоторые другие свойства показаны на большем графе.
Деревья уже изучались подробно в
“Абстрактные типы данных”
, а здесь мы рассмотрим различные эквивалентные определения. Например, граф G с Vвершинами является деревом тогда и только тогда, когда он удовлетворяет любому из следующих четырех условий:
- G содержит V-1 ребро и ни одного цикла.
- G содержит V-1 ребро и является связным.
- Каждую пару вершин в G соединяет в точности один простой путь.
- G является связным, а при удалении любого из ребер перестает быть связным.
Любое из указанных выше условий необходимо и достаточно для доказательства остальных трех, и из них можно вывести другие свойства деревьев (см. упражнение 17.1). Формально следовало бы выбрать одно из этих условий в качестве определения; но неформально они могут служить определениями все вместе и свободно заменять, например, слова ” ациклический связный граф ” в определении 17.4.
Графы, у которых присутствуют все ребра (т.е. между каждыми двумя вершинами -прим. перев.), называются полными графами (complete graph) -см.
рис.
17.4. Дополнение (complement) графа G определяется так: берется полный граф с тем же множеством вершин, что и исходный графа G, и из него удаляются все ребра графа G.
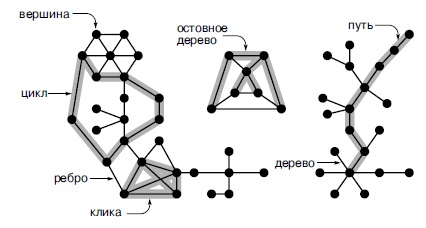
Рис.
17.3.
Терминология, употребляемая в теории графов
Этот граф содержит 55 вершин, 70 ребер и 3 связных компонента. Один из связных компонентов представляет собой дерево (справа). В графе имеется множество циклов, один из них выделен как крупный связный компонент (слева). На диаграмме также показано остовное дерево небольшого связного компонента (в центре). Весь граф не может иметь остовного дерева, поскольку он не является связным.
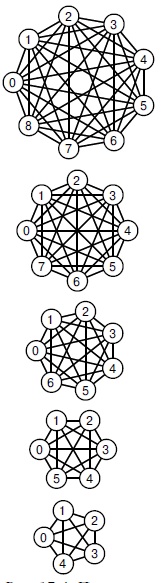
Рис.
17.4.
Полные графы
Здесь показаны полные графы, в которых каждая вершина соединена с любой другой вершиной. Они содержат, соответственно, 10, 15, 21, 28 и 36 ребер (снизу вверх). Каждый граф, содержащий от 5 до 9 вершин (существует более 68 миллиардов таких графов), является подграфом одного из этих графов.
Объединением (union) двух графов является граф, порожденный объединением множеств ребер этих графов. Объединение графа и его дополнения дает полный граф. Все графы, имеющие V вершин, являются подграфами полного графа с V вершинами. Общее количество различных графов с V вершинами равно 2<sup>V(V- 1)/2</sup> (количество различных подмножеств из V( V-1)/2 возможных ребер). Полный подграф называется кликой (clique).
Большинство встречающихся на практике графов содержат лишь небольшую часть всех возможных ребер. Для численного выражения этой концепции определим насыщенность (density) графа равной среднему значению степеней его вершин, т.е. 2E/V. Граф называется насыщенным (dense graph), если средняя степень его вершин близка к V; разреженный граф (sparse graph) есть граф, дополнение которого насыщенно. Другими словами, мы считаем граф насыщенным, если количество его ребер E имеет порядок V2, и разреженным в противном случае. Такое ” асимптотическое ” определение не очень точно характеризует графы, однако различие очевидно: можно с уверенностью утверждать, что граф, состоящий из миллионов вершин и десятков миллионов ребер, является разреженным, а граф, состоящий из нескольких тысяч вершин и миллионов ребер, является насыщенным. Можно браться за обработку разреженного графа с миллиардами вершин, но насыщенный граф с миллиардами вершин содержит несметное количество ребер.
Информация о том, с каким графом мы имеем дело -с насыщенным или разреженным -обычно является главным фактором выбора эффективного алгоритма обработки графа. Например, для решения какой-то задачи мы можем разработать два алгоритма, и первому из них для ее решения понадобится V2 шагов, а другому -E lgE шагов. Эти формулы показывают, что второй алгоритм лучше подходит для разреженных алгоритмов, а первый алгоритм следует применять для насыщенных графов. Например, насыщенный граф с миллионами ребер может иметь всего лишь несколько тысяч вершин: в этом случае величины V2 и E имеют один порядок, а быстродействие алгоритма сложности V2 в 20 раз выше, чем быстродействие алгоритма сложности ElgE. С другой стороны, разреженный граф с миллионами ребер будет иметь и миллионы вершин, следовательно, алгоритм сложности E lgE будет в миллионы раз быстрее алгоритма со сложностью V2. Подробное изучение этих формул может привести к различным вариантам, но для практических целей обычно вполне достаточно терминов разреженный и насыщенный, чтобы можно было получить представление об основных характеристиках производительности.
При анализе алгоритмов обработки графов мы полагаем, что значение V/E ограничено сверху небольшой константой, и поэтому такие выражения, как V(V+E), можно упростить до VE. Это предположение нарушается только если количество ребер гораздо меньше количества вершин, что бывает крайне редко. Как правило, количество ребер намного превосходит количество вершин (V/E намного меньше 1).
Двудольный граф (bipartite graph) -это граф, множество вершин которого можно разбить на два таких подмножества, что любое ребро соединяет вершину из одного подмножества с вершиной из другого подмножества. Пример двудольного графа приведен на
рис.
17.5. Двудольные графы естественным образом возникают во многих ситуациях, таких как задачи поиска сопоставлений, описанные в начале этой главы. Любой подграф двудольного графа сохраняет это свойство.
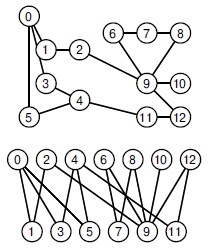
Рис.
17.5.
Двудольный граф
Все ребра данного графа соединяют вершины с нечетными номерами с вершинами с четными номерами -т.е. это двудольный граф. Дву-дольность наглядно видна на нижней диаграмме.
Графы, которые мы рассматривали до сих пор, носят название неориентированных (undirected) графов. В ориентированных (directed) графах, известных еще как орграфы (digraph), ребра имеют направления: пара вершин, определяющая любое ребро, рассматривается как упорядоченная пара, которая определяет направленную смежность -в том смысле, что можно перейти из первой вершины во вторую, но не из второй вершины в первую. Многие приложения (например, графы, представляющие всемирную компьютерную сеть, или расписания действий, или телефонные звонки) естественным образом описываются как раз орграфами.
Ребра в орграфах называются ориентированными ребрами (directed edge), хотя обычно это свойство понятно из контекста (некоторые авторы называют ориентированные ребра дугами -arc). Первая вершина ориентированного ребра называется началом (source), а вторая вершина концом (destination). (Некоторые авторы употребляют, соответственно, термины хвост (tail) и голова (head), чтобы подчеркнуть, что это вершины ориентированного графа, однако мы будем избегать таких обозначений, поскольку употребляем эти же термины в реализациях структур данных.) На диаграммах ориентированные ребра изображаются в виде стрелок, направленных из начала в конец, и часто говорим, что ребро указывает (point) на конечную вершину. Обозначение w-v в орграфе означает, что это ребро, которое указывает из w на v, и оно отличается от ребра v-w, которое указывает из v на w. Мы также говорим о степени выхода (outdegree) и степени захода (indegree) вершины -это, соответственно, количество ребер, для которых она служит началом, и количество ребер, для которых она служит концом.
Иногда неориентированный граф удобнее рассматривать как орграф, у которого вместо каждого неориентированного ребра имеются два ориентированных ребра (по одному в каждом направлении); в других случаях неориентированный граф бывает лучше рассматривать просто как совокупность связей. Как правило, и для ориентированных, и для неориентированных графов мы используем одно и то же представление (см.
рис.
17.6), о чем подробно пойдет речь в разделе 17.4. То есть обычно для неориентированных графов мы поддерживаем два представления каждого ребра -по одному для каждого направления -чтобы иметь возможность сразу же ответить на вопросы типа ” Какие вершины связаны с вершиной v? ”
Изучению структурных свойств орграфов посвящена
“Орграфы и DAG-графы”
; обычно они более сложны, чем соответствующие свойства неориентированных графов. Направленный цикл (directed cycle) в орграфе -это цикл, в котором пары смежных вершин появляются в порядке, указываемом ребрами графа. DAG-граф (Directed Acyclic Graph -ориентированный ациклический граф) представляет собой орграф, который не содержит направленных циклов. DAG-граф (ациклический орграф) не эквивалентен дереву (ациклическому неориентированному графу). Иногда мы рассматриваем базовый неориентированный граф (underlying undirected graph) орграфа, то есть неориентированный граф, определяемый тем же множеством ребер, только эти ребра не рассматриваются как ориентированные.
Главы 20—22 посвящены в основном анализу алгоритмов решения различных вычислительных задач, связанных с использованием графов, в вершинах и ребрах которых хранится дополнительная информация. В случае взвешенного графа (weighted graph) с каждым ребром связано число (weight -вес), которое обычно интерпретируется как расстояние либо стоимость. Можно также присвоить вес каждой вершине, либо несколько весов каждой вершине и каждому ребру. В
“Минимальные остовные деревья”
мы будем изучать взвешенные неориентированные графы, а в
“Кратчайшие пути”
и
“Потоки в сетях”
-взвешенные орграфы, которые называют сетями (network). Алгоритмы, рассматриваемые в
“Потоки в сетях”
, решают классические задачи, которые возникают при особой интерпретации сетей, известной как сетевые потоки (flow network).
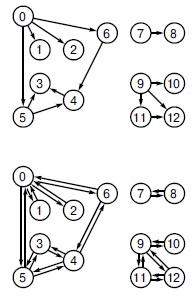
Рис.
17.6.
Два орграфа
Верхний рисунок является представлением графа, приведенного на
рис.
17.1, который интерпретируется как ориентированный граф; при этом ребра считаются упорядоченными парами и изображаются в виде стрелок, ведущих из первой вершины во вторую. Этот граф является также и DAG-графом. Нижний рисунок -это изображение неориентированного графа с
рис.
17.1, которое обычно выбирается нами для представления неориентированных графов: в виде орграфа, в котором каждой связи соответствуют два ребра (по одному в каждом направлении).
Уже в
“Введение”
было понятно, что комбинаторная структура графа получила широкое распространение. Масштаб распространения этой структуры тем более поразителен, если учесть, что в ее основе лежит простая математическая абстракция. Эта простота видна во многих кодах, которые мы разработаем для базовой обработки графов. Однако такая простота часто заслоняет собой сложные динамические свойства, которые требуют глубокого понимания комбинаторных свойств самих графов. Зачастую даже трудно поверить, что алгоритм, записываемый таким компактным кодом, действительно работает.
Упражнения
17.1. Докажите, что любой ациклический связный граф с V вершинами имеет V-1 ребро.
17.2. Приведите все связные подграфы графа 0-1 0-2 0-3 1-3 2-3.
17.3. Составьте список неизоморфных циклов графа, представленного на
рис.
17.1. Например, если в списке содержится цикл 3-4-5-3, то в нем не могут находиться циклы 3-5-4-3 , 4-5-3-4 , 4-3-5-4 , 5-3-4-5 или 5-4-3-5 .
17.4. Пусть дан граф 4-7 1-4 7-8 0-5 5-2 3-8 2-9 0-6 4-9 2-6 6-4
Определите количество связных компонентов, постройте остовный лес, составьте список всех простых путей, содержащих не менее трех вершин, а также список всех неизоморфных циклов (см. упражнение 17.3).
17.5.
Пусть даны графы, определяемые следующими четырьмя наборами ребер:
0-10-20-31-31-42-52-93-64-74-85-85-96-76-97-8
0-10-20-30-31-42-52-93-64-74-85-85-96-76-97-8
0-11-21-30-30-42-52-93-64-74-85-85-96-76-97-8
4-17-96-27-35-00-20-81-63-96-32-81-59-84-54-7
Какие из этих графов изоморфны друг другу? Какие из них планарны?
17.6. Какой процент из более чем 68 миллиардов графов, о которых говорится в подписи к
рис.
17.4, состоит из менее чем девяти вершин?
17.7. Сколько различных подграфов имеется в заданном графе с V вершинами и E ребрами?
17.8. Приведите максимально точные верхние и нижние границы количества связных компонентов графа с V вершинами и E ребрами.
17.9. Сколько существует неориентированных графов, содержащих V вершин и E ребер?
17.10. Сколько существует различных графов, содержащих V вершин и E ребер, если считать графы различными, только когда они не изоморфны?
17.11. Сколько графов, содержащих V вершин, являются двудольными?
Источник
