Какие свойства имеет высота
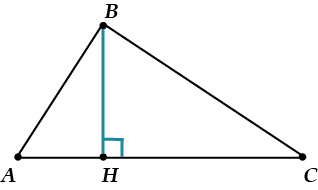
Там, где есть высота, есть и прямой угол.
А значит, и прямоугольный треугольник, который поможет тебе решить массу задач!
И простые подобия, и «хитрые подобия с косинусом», и другие свойства прямоугольных треугольников!
И самое главное – не нужно ничего запоминать.
Научись выводить и никогда не ошибёшься, сможешь всегда себя проверить и решить любую задачу!
Все в этой статье. Читай.
НАЧАЛЬНЫЙ УРОВЕНЬ
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
Давай нарисуем:
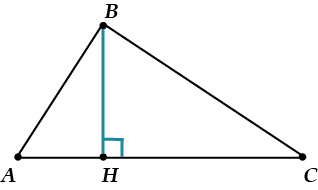
На этом рисунке ( displaystyle BH) – высота.
Но иногда высота ведёт себя, как непослушный ребенок – «выбегает» из треугольника. Это бывает в тупоугольном треугольнике.
И тогда получается так:
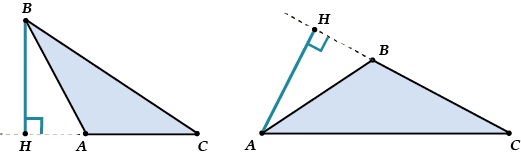
В общем, не нужно пугаться, если основание высоты оказалось не на стороне треугольника, а «за» треугольником, на продолжении стороны. Как же решать задачи, в которых участвует высота?
Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.
Давай попробуем.
Пример решения задачи
Вот есть, скажем, задача:
В треугольнике ( displaystyle ABC) с тупым углом ( displaystyle C) проведена высота ( displaystyle BH). Найти ( displaystyle AC), если ( AB=2sqrt{10}), ( BC=sqrt{13}), ( BH=2).
Решаем:
Это закрытый контент
Оставьте E-mail и получите на почту доступ к нему
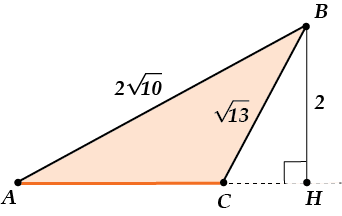
Смотри: из-за того, что угол ( C) – тупой, высота ( BH) опустилась на продолжение стороны ( AC), а не на саму сторону.
Теперь давай увидим во всём этом два прямоугольных треугольника.
Смотри их целых два:
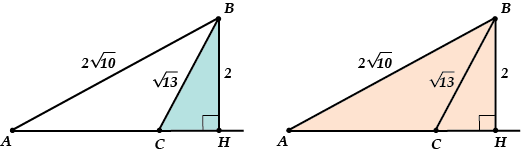
Применяем теорему Пифагора к треугольнику ( BCH):
( B{{C}^{2}}=B{{H}^{2}}+C{{H}^{2}}), то есть ( 13=4+C{{H}^{2}}); ( CH=3).
А теперь теорема Пифагора для ( Delta ABH):
( A{{B}^{2}}=A{{H}^{2}}+B{{H}^{2}}); то есть ( 40=A{{H}^{2}}+4); ( AH=6).
Теперь осталось только заметить, что ( AC=AH-CH=6-3=3).
Нашли!
Пересечение высот
А теперь давай зададимся вопросом: а сколько вообще высот у треугольника? Конечно, три! И вот, есть такое утверждение, доказывать которое мы здесь не будем, но знать его нужно, тем более, что запоминается оно просто:
В любом треугольнике все три высоты (или их продолжения) пересекаются в одной точке.
Смотрим, как это бывает:
a) Сами высоты пересекаются:
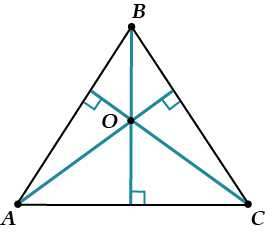
b) Пересекаются продолжения:
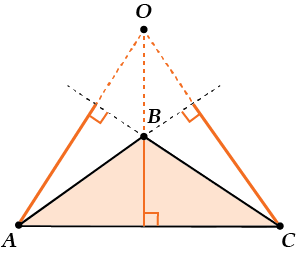
Ну вот, про высоту и запоминать-то нужно всего ничего:
- Задача про высоту часто решается с помощью знаний о прямоугольном треугольнике.
- Три высоты (или три продолжения) пересекаются в одной точке.
(Но! Это НЕ центр НИКАКОЙ окружности)
СРЕДНИЙ УРОВЕНЬ
Высота треугольника –линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, содержащей эту высоту).
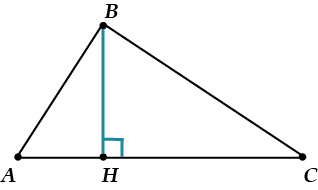
Обрати внимание, что, в отличие от биссектрисы и медианы,высота может находиться вне треугольника. Вот так, например:

Немного о терминологии: основанием высоты называют ту точку, в которой высота пересекает противоположную сторону (или её продолжение).
Задачи, связанные с высотой, часто решаются при помощи знаний о прямоугольном треугольнике. Но попадаются задачи и похитрее, при решении которых лучше обладать дополнительными знаниями заранее, а не выводить их «с нуля». Сейчас мы обсудим некоторые из них.
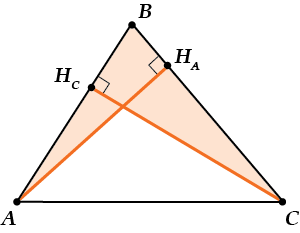
Первый «неожиданный факт»:
( displaystyle Delta AB{{H}_{A}}sim Delta ~CB{{H}_{C}})
Почему бы это? Да очень просто! У них общий угол ( displaystyle B) и оба – прямоугольные. Значит, подобны по двум углам.
Второй «неожиданный» факт:
( Delta A{{H}_{C}}Hsim{ }Delta C{{H}_{A}}H)
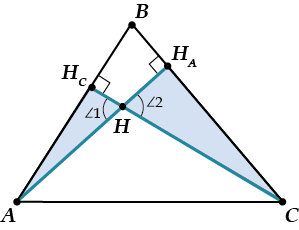
Здесь тоже подобие по двум углам: ( angle 1=angle 2) (как вертикальные) и по прямому углу.
Третий, по-настоящему неожиданный факт:
Это закрытый контент
Оставьте E-mail и получите на почту доступ к нему
( Delta ABCsim Delta {{H}_{A}}B{{H}_{C}})
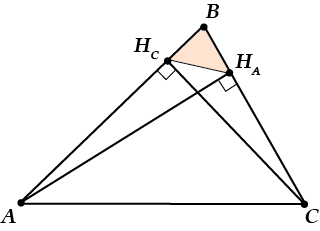
Вот это уже интереснее, правда? Давай разбираться, почему так.
- Во-первых, конечно, у этих треугольников есть одинаковый (и даже общий) угол ( B).
- А во-вторых… Ты помнишь ещё первый “неожиданный” факт? Ну, что ( Delta A{{H}_{A}}Bsim Delta C{{H}_{C}}B)? Вспоминаем и применяем!
Запишем отношения соответствующих сторон.
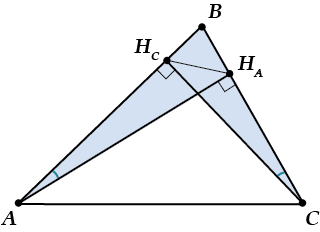
Итак, ( Delta A{{H}_{A}}Bsim Delta C{{H}_{C}}B).
Следовательно, ( frac{{{H}_{C}}B}{{{H}_{A}}B}=frac{BC}{AB})
Перепишем по–другому: ( frac{{{H}_{C}}B}{BC}=frac{{{H}_{A}}B}{AB})
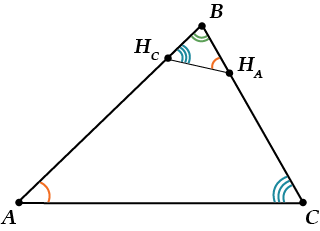
Ух, да это же – отношение сторон для треугольников ( ABC) и ( {{H}_{A}}B{{H}_{C}})!
В итоге мы получили, что у треугольников ( ABC) и ( {{H}_{A}}B{{H}_{C}})
- Угол ( B) – общий;
- Отношение сторон, заключающих этот угол – одинаковы: ( frac{{{H}_{C}}B}{BC}=frac{{{H}_{A}}B}{AB}).
Значит, мы получили, что:
( Delta ABCsim Delta {{H}_{A}}B{{H}_{C}})
Но самое интересное ещё впереди!
Каков же коэффициент подобия этих треугольников? То есть чему же равно это самое отношение ( frac{{{H}_{C}}B}{BC})?
Рисуем:
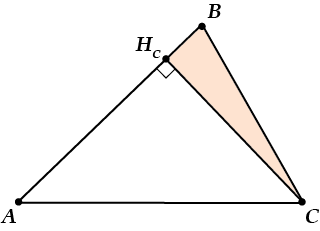
Где наши знания о прямоугольном треугольнике?
Что такое ( {{H}_{C}}B)? Катет, прилежащий к углу ( B).
А что такое ( BC)? Гипотенуза!
Значит, ( frac{{{H}_{C}}B}{BC}=cosangle B).
Потрясающе, не правда ли?
Давай сформулируем ещё раз, чтобы лучше запомнить:

( displaystyle Delta {{H}_{A}}B{{H}_{C}}sim Delta ABC)( k=cos angle B)
Ну вот, две высоты в треугольнике рассмотрены. А теперь…
В треугольнике проведены три высоты
Как и для медиан, и для биссектрис, для высот треугольника верно следующее утверждение:
В любом треугольнике три высоты или их продолжения пересекаются в одной точке.
Доказывать это утверждение мы здесь, пожалуй, не будем.
Давай просто нарисуем, чтобы понять, как это бывает «высоты или их продолжения».
1. Треугольник остроугольный – тогда пересекаются сами высоты:
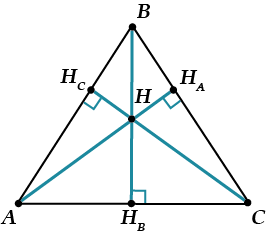
2. Треугольник тупоугольный – тогда пересекаются продолжения высот:
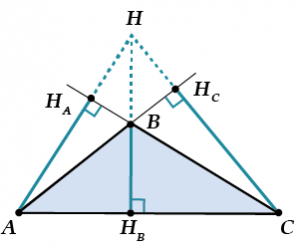
Что же полезного мы ещё не обсудили?
Угол между высотами
Давай узнаем, вдруг угол между высотами можно как–то выразить через углы треугольника? Давай рассмотрим остроугольный треугольник.
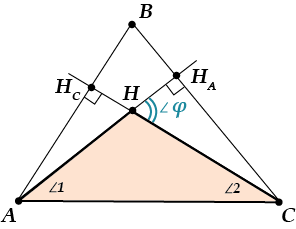
Итак, нам хотелось бы найти ( displaystyle angle varphi ).
Смотрим на ( displaystyle Delta AHC). Замечаем, что наш ( displaystyle angle varphi ) – внешний угол в этом треугольнике.
Значит, ( angle varphi =angle 1+angle 2).
Чему же равны ( displaystyle angle 1) и ( displaystyle angle 2)?
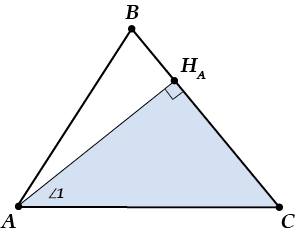
Смотри: из ( Delta A{{H}_{A}}C) выходит, что ( angle 1=90{}^circ -angle C).
Конечно, таким же образом из ( Delta C{{H}_{C}}A) получается, что ( angle 2=90{}^circ -angle A).
Теперь ( angle ~varphi =angle ~1+angle ~2=90{}^circ -angle ~C+90{}^circ -angle ~A=180{}^circ -angle ~A-angle ~C).
Но что же это такое? Ведь сумма угла углов треугольника – ( 180{}^circ )! Значит, ( angle varphi =angle B).
Итак, что получилось?
Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
А как же дело обстоит в тупоугольном треугольнике? Давай смотреть…очень внимательно!
Представим, что у нас «главный» не ( displaystyle Delta ABC), а ( displaystyle Delta AHC).
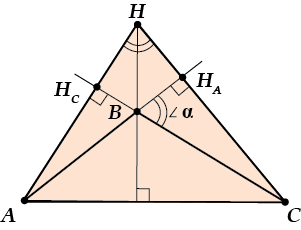
Тогда оказывается, что прямые ( displaystyle AB), ( displaystyle BC) и ( displaystyle HB) – высоты в ( displaystyle Delta AHC).
Но ( displaystyle Delta AHC) уже остроугольный (так как все высоты оказались внутри), а про остроугольный треугольник мы уже всё знаем: ( displaystyle angle alpha =angle H).
НО! ( displaystyle angle alpha =180{}^circ -angle B)
Значит, для тупоугольного треугольника:
( angle ~H=180{}^circ -angle ~B).
И ещё кое–что…
Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:
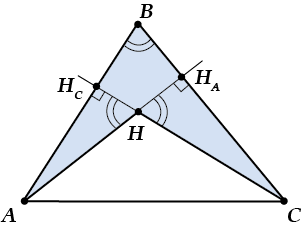
Что видим теперь? Ещё подобные треугольники!
Как от двух линий вообще могут получиться столько подобных треугольников?!
Но тем не менее…
( Delta C{{H}_{C}}Bsim Delta C{{H}_{A}}Hsim Delta A{{H}_{A}}Bsim Delta A{{H}_{C}}H)
Видишь, какое богатство? И всё это может быть использовано в задачах!
Ну вот, теперь ты узнал что-то новенькое про высоты треугольника. Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее – которое с косинусом, и то, что угол между высотами равен углу между сторонами…
Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести. И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
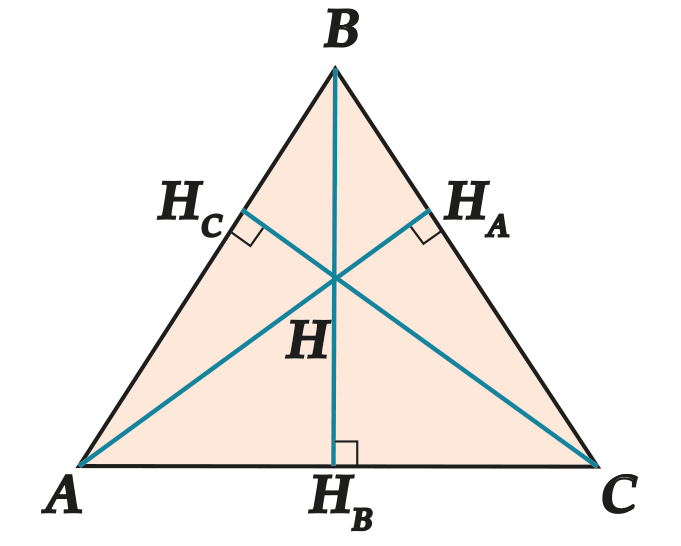
Три высоты любого треугольника пересекаются в одной точке.
Высоты треугольника обратно пропорциональны сторонам, на которые они опущены: ( displaystyle A{{H}_{A}}:B{{H}_{B}}:C{{H}_{C}}=frac{1}{BC}:frac{1}{AC}:frac{1}{AB}).
Способы вычисления длины высоты, проведенной к стороне BC:
- Через сторону и угол треугольника: ( displaystyle A{{H}_{A}}=ACcdot sin C=ABcdot sin B).
- Через все 3 стороны треугольника:( displaystyle A{{H}_{A}}=frac{2}{BC}cdot sqrt{pcdot (p-BC)cdot (p-AC)cdot (p-AB)}),где ( displaystyle p) – полупериметр треугольника: ( displaystyle p=frac{AB+BC+AC}{2}).
- Через сторону и площадь треугольника: ( displaystyle A{{H}_{A}}=frac{2S}{BC}).
- Через стороны треугольника и радиус описанной окружности:
( displaystyle A{{H}_{A}}=frac{ABcdot AC}{2R}),где ( displaystyle R) – радиус описанной окружности.
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Твоя очередь!
Ты знаешь очень много о высоте треугольника. И вот, что нужно сделать дальше. Практикуйся! Ведь я уверен, что с каждой задачей ты будешь все увереннее применять свои знания!
Высота треугольника – не просто перпендикуляр, длину которого мы используем для нахождения площади, верно? Это кое-что покруче ????
А теперь мы хотим узнать твое мнение!
Помогла ли тебе эта статья? Понравилась ли она тебе и все ли было понятно?
Напиши внизу в комментариях!
А если остались вопросы, задай их! Мы непременно ответим тебе!
Успехов!
Источник
Анонимный вопрос
6 июня 2018 · < 100
Самая высокая гора в мире?
Самая большая гора в мире Эверест , ещё ее называют Джомолунгма. Вершину этой горы ежегодно пытаются покорить тысячи альпинистов, собирается огромное количество экспедиций,но до вершины доходят далеко не все. Большинство либо возвращаются домой, осознав , что сил для восхождения у них пока недостаточно, либо остаются в горах навечно. В любом случае, покорить эту высоту могут только самые подготовленные, смелые и сильные альпинисты.
Прочитать ещё 9 ответов
Как ориентироваться по компасу?
Педагог, музыкант, начинающий путешественник и немножко психолог
Особенность компаса такова, что его стрелка всегда указывает на север. Для большей точности положите прибор на ровную поверхность параллельно земле. Разверните его так, чтобы север был наверху – на 12 часов по аналогии с циферблатом. Теперь Вы легко сможете определить остальные стороны горизонта: внизу юг, слева запад, справа восток. Зная направление движения, наметьте себе ориентир на местности и идите к нему. Чтобы не сбиться, периодически сверяйтесь с компасом и находите новые ориентиры.
Прочитать ещё 2 ответа
Какая теорема в геометрии не доказана?
Кандидат физ.-мат. наук, делаю Яндекс, увлекаюсь всем на свете
Например, если вы докажете гипотезу Ходжа, то вы получите приз в миллион долларов. К сожалению, даже формулировку этой гипотезы объяснить неспециалисту практически невозможно. Достаточно сказать, что речь в ней идёт не о двумерных конструкциях (как в школьной геометрии) и не о трехмерных (как в стереометрии), а о многомерных, координаты в этих пространствах не обычные числа, а комплексные. И это только начало.
До 2003 года был чуть более простой для восприятия пример важной недоказанной геометрической теоремы, так называемая гипотеза Пуанкаре (тоже “задача на миллион”). Но эту задачу решил российский математик Григорий Перельман, а от миллиона отказался. Наверное, вы что-нибудь об этом слышали!
Прочитать ещё 11 ответов
Сколько весит тень?
физик-теоретик в прошлом, дауншифтер и журналист в настоящем, живу в Германии
Вес (в физике) – это сила, с которой тело давит на опору. Обычно его путают с массой, так как в гравитационном поле Земли вес пропорционален массе, а коэффициент пропорциональности (ускорение свободного падения) практически неизменен. Также и во вращающейся неинерциальной системе (например, во вращающейся космической станции) центробежная сила (а с нею и вес объектов) будет пропорциональна их массе, но коэффициент пропорциональности будет уже иным.
Теперь о тени. Конечно, это не объект. И массы у нее нет. Тем не менее, в некотором смысле у тени есть вес. Только он – отрицательный!
Ведь тень – это отсутствие света из-за вставшей на его пути преграды. Свет – это поток фотонов, имеющих массу и скорость, а с ними и импульс. Если бы фотоны долетали, они передавали бы свои импульсы освещенной “опоре”, оказывая непрерывное давление. А давление, умноженное на площадь – это сила. Можно сказать, вес света. Ну а тень – это отсутствие и света и его “веса”. То есть, по сравнению с освещением тень как бы имеет “отрицательный” вес, примерно как “дырка” (нехватка отрицательно заряженного электрона в полупроводнике) “имеет” положительный заряд.
Прочитать ещё 3 ответа
Возможен ли не прямоугольный треугольник, в котором сумма квадратов двух сторон равна квадрату третьей стороны?
Я согласен с ответом от Uwe Boll, но постараюсь ответить более детально.
Вообще, если вам даны один угол и длина двух сторон, или два угла и длина одной стороны, или все три стороны, то они определяют остальные три элемента. Однако если вам даны три угла, то они определяют длину сторон с точностью до фактора.
В вашем вопросе, даны длины всех трех сторон с точностью до фактора:
fA, fB, и fC=f sqrt(A^2+B^2). Мы хотим понять почему никакой “гибкости” в этом треугольнике нет.
Обозначим углы напротив каждой из сторон соотвенственно a, b, c .
Мы используем закон косинусов на плоскости:
Косинус угла напротив “длинной” стороны (мы подозреваем, гипотенузы) определен
cos(c) = (A^2 + B^2 – C^2) / (2AB)
(фактор f сокращается). (Заметим, что два других угла тоже определены без всякой гибкости, но нам они не интересны.) Дальже идет алгебра – мы знаем длину C(A,B) и подставляем в правую сторону:
(A^2 + B^2 – C^2) / (2AB) = (A^2 + B^2 – sqrt(A^2+B^2)^2) / (2AB) = (A^2 + B^2 – (A^2+B^2)) / (2AB) = 0.
То есть косинус угла c = ноль. Значит это должен быть прямой угол.
Однако закон косинусов так не работает, если ваш треугольник не на плоскости, а, например, на сфере.
Прочитать ещё 2 ответа
Источник
Почти никогда не получится определить все параметры треугольника без дополнительных построений. Эти построения являются своеобразными графическими характеристиками треугольника, которые помогают определить величину сторон и углов.

Определение
Одной из таких характеристик является высота треугольника. Высота – это перпендикуляр, проведенный из вершины треугольника к его противоположной стороне. Вершиной называют одну из трех точек, которые вместе с тремя сторонами составляют треугольник.
Определение высоты треугольника может звучать и так: высота – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Это определение звучит сложнее, но оно точнее отражает ситуацию. Дело в том, что в тупоугольном треугольнике не получится провести высоту внутри треугольника. Как видно на рисунке 1, высота в этом случае получается внешней. Кроме того, не стандартной ситуацией является построение высоты в прямоугольном треугольнике. В этом случае, две из трех высот треугольника будут проходить через катеты, а третья от вершины к гипотенузе.
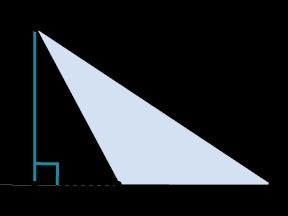
Рис. 1. Высота тупоугольного треугольника.
Как правило, высота треугольника имеет обозначение буквой h. Так же обозначается высота и в других фигурах.
Как найти высоту треугольника?
Существует три стандартных способа нахождения высоты треугольника:
Через теорему Пифагора
Этот способ применяется для равносторонних и равнобедренных треугольников. Разберем решение для равнобедренного треугольника, а потом скажем, почему это же решение справедливо для равностороннего.
Дано: равнобедренный треугольник АВС с основанием АС. АВ=5, АС=8. Найти высоту треугольника.
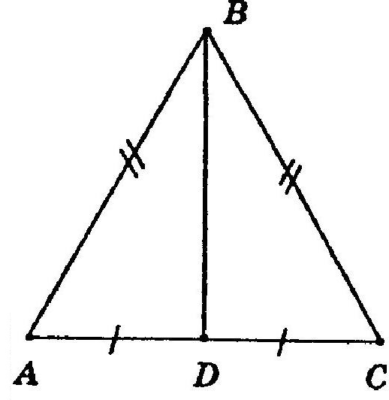
Рис. 2. Рисунок к задаче.
Для равнобедренного треугольника важно знать, какая именно сторона является основанием. Это определяет боковые стороны, которое должны быть равны, а так же высоту, на которую действую некоторые свойства.
Свойства высоты равнобедренного треугольника, проведенной к основания:
- Высота совпадает с медианной и биссектрисой
- Делит основание на две равные части.
Высоту обозначим, как ВD. DС найдем как половину от основания, так как высота точкой D делит основание пополам. DС=4
Высота это перпендикуляр, значит ВDС – прямоугольный треугольник, а высота ВН является катетом этого треугольника.
Найдем высоту по теореме Пифагора: $$ВD=sqrt{BC^2-HC^2}=sqrt{25-16}=3$$
Любой равносторонний треугольник является равнобедренным, только основание у него равно боковым сторонам. То есть, можно использовать тот же порядок действий.
Через площадь треугольника
Этим способом можно пользоваться для любого треугольника. Чтобы им воспользоваться, нужно знать значение площади треугольника и стороны, к которой проведена высота.
Высоты в треугольнике не равны, поэтому для соответствующей стороны получится вычислить соответствующую высоту.
Формула площади треугольника: $$S={1over2}*bh$$, где b – это сторона треугольника ,а h – высота, проведенная к этой стороне. Выразим из формулы высоту:
$$h=2*{Sover b}$$
Если площадь равна 15, сторона 5, то высота $$h=2*{15over5}=6$$
Через тригонометрическую функцию
Третий способ подойдет, если известна сторона и угол при основании. Для этого придется воспользоваться тригонометрической функцией.
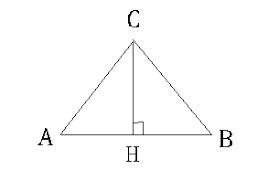
Рис. 3. Рисунок к задаче.
Угол ВСН=300 , а сторона BC=8. У нас все тот же прямоугольный треугольник BCH. Воспользуемся синусом. Синус это отношение противолежащего катета к гипотенузе, значит: BH/BC=cos BCH.
Угол известен, как и сторона. Выразим высоту треугольника:
$$BH=BC*cos (60unicode{xb0})=8*{1over2}=4$$
Значение косинуса в общем случае берется из таблиц Брадиса, но значения тригонометрических функций для 30,45 и 60 градусов – табличные числа.
Что мы узнали?
Мы узнали, что такое высота треугольника, какие бывают высоты и как они обозначаются. Разобрались в типовых задачах и записали три формулы для высоты треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.6. Всего получено оценок: 231.
Источник
