Какие свойства имеет круг

Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
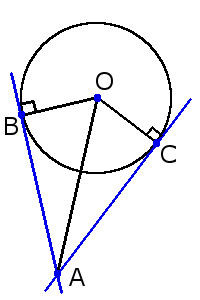
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
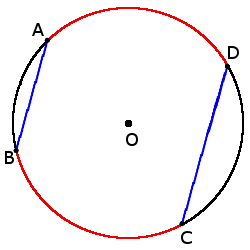
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
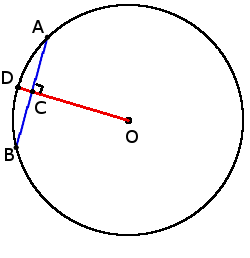
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
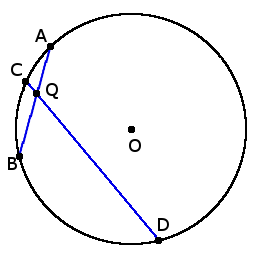
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
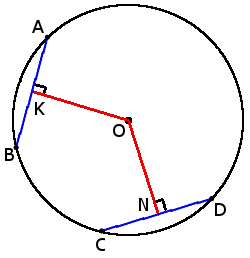
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
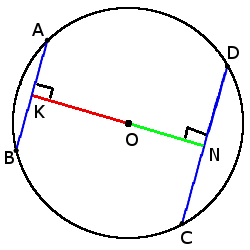
6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
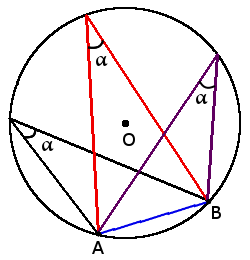
1. Все вписанные углы, которые опираются на одну дугу – равны.
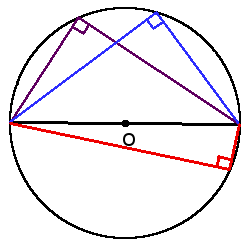
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
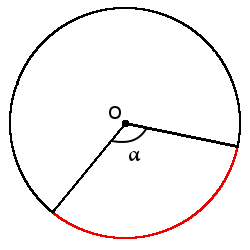
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
Что такое окружность?
Окружность — одна из самых важных кривых линий на плоскости, её можно начертить циркулем или даже натянутой верёвкой, если закрепить один из концов верёвки в данной точке. В любом случае расстояние от всех точек окружности до данной закреплённой точки будет одинаково. Эту точку называют центром окружности, а любой отрезок, который соединяет точку на окружности с её центром, называется радиусом. В переводе с латыни слово радиус означает “спица колеса”. Это не удивительно, ведь можно сказать, что окружность — это математическая модель колеса. Если две любые точки окружности соединить отрезком, то получится хорда. Хорда же в переводе с греческого языка означает “струна”. Если хорда проходит через центр окружности, то её называют диаметром и обычно обозначают буквой . Понятно, что длина диаметра окружности должна быть равна двум её радиусам, то есть . Давайте повторим ещё раз.
Определения.
Окружность — это множество всех точек на плоскости, находящихся на одинаковом расстоянии от данной точки.
Радиус окружности — отрезок, соединяющий любую её точку с центром. Все радиусы окружности равны.
Хорда окружности — отрезок, соединяющий две любые её точки.
Диаметр окружности — это хорда, которая проходит через центр окружности.
Свойство диаметра.
Легко доказать, что диаметр окружности — это самая длинная её хорда. Да, и само слово диаметр в переводе означает “поперечник”. В технике измеряют диаметры колёс, труб, винтов и гвоздей и обозначают их таким значком .
Давайте сформулируем данное свойство диаметра как теорему.
Теорема.
Любая хорда окружности не превышает её диаметра.
Доказательство. Возьмём на окружности с центром в точке и радиусом любые две точки и . Если хорда проходит через центр окружности, то по определению она будет её диаметром и равна . Если же хорда не содержит центра окружности, то образуется треугольник . Тогда для него должно выполняться неравенство треугольника: . Значит, в любом случае хорда не может быть больше диаметра окружности. Что и требовалось доказать.
Полезно знать, что в геометрии диаметр можно определить не только для окружности или круга. Он есть у квадрата, треугольника, да и вообще у многих других геометрических фигур. А знаете, что называют диаметром фигуры? Так же, как и у окружности, диаметр фигуры — это самая длинная её хорда.
Определение.
Диаметр геометрической фигуры — это самое большое расстояние между любыми двумя точками этой фигуры.
Что такое круг?
Чем круг отличается от окружности? Каждый человек интуитивно понимает, что круг — это то, что находится “внутри ” окружности. Можно даже сказать, что для окружности круг — это её внутренняя область. Правда, работать с таким определением не очень удобно.
Как же можно удобно определить круг? Предположим, что один фермер выпустил пастись свою козу на луг, а чтобы она далеко не ушла, привязал её к колышку в точке с помощью верёвки длины . В течение дня коза выщипала траву везде, куда она смогла дотянуться. Как выглядит та часть луга, где паслась коза, и где теперь не стало травы?
Ясно, что коза не сможет отойти от колышка, к которому она привязана, дальше чем на длину своей верёвки. И она сможет дотянуться до любого места, которое ближе находится к этому колышку, чем длина её верёвки. Таким образом, коза выщиплет траву внутри круга с центром в точке и радиусом , равным длине её натянутой верёвки. Теперь мы с вами уже можем дать следующее определение.
Определение.
Круг — это множество всех точек плоскости, удалённых от данной точки не более, чем на длину данного отрезка.
Данная точка называется центром круга, а указанный отрезок — радиусом круга.
Круг с центром в точке и радиусом обозначают так: круг .
Разберём несколько примеров решения задач.
Пример 1. В окружности провели две хорды и , равные радиусу этой окружности. Найдите угол .
Решение. Отметим центр данной нам окружности и проведем радиусы в точки , и . Тогда треугольники и будут равносторонними. Значит, их углы и будут равны . Искомый угол равен их сумме, поэтому он будет равен .
Ответ: .
Пример 2. В окружность радиуса вписан квадрат. Найдите площадь этого квадрата.
Решение. Отметим центр данной нам окружности и проведем из него радиусы во все вершины квадрата .
Поскольку у квадрата все стороны равны, а радиусы окружности равны по определению, треугольники , , и будут равны по трём сторонам. Значит, равны все их углы при вершинах в точке . Сумма этих четырёх углов равна , поэтому каждый угол равен .
Запишем теорему Пифагора для треугольника : . Значит, сторона квадрата равна , а его площадь равна квадрату стороны. То есть, она равна .
Ответ: .
Пример 3. В окружность радиуса вписан равносторонний треугольник. Найдите расстояние от центра окружности до стороны этого треугольника.
Решение. Соединим центр окружности с вершинами равностороннего треугольника , который вписан в эту окружность. Поскольку все стороны треугольника равны, а радиусы окружности равны по определению, то равнобедренные треугольники , и будут равны по трём сторонам. Поэтому будут равны шесть углов при основаниях этих треугольников. Обозначим величину каждого из них через и запишем сумму всех углов треугольника : . Откуда .
Расстояние от точки до прямой линии — это длина перпендикуляра, опущенного из этой точки на данную прямую. Давайте опустим из точки перпендикуляр на сторону нашего треугольника и найдём его длину. Треугольник будет прямоугольным, причём его угол при вершине будет равен . Значит, по известному свойству катет против угла равен половине гипотенузы. То есть, .
Ответ: .
Источник

Хорошо известно определение окружности как геометрического места точек, равноудаленных от некоторой фиксированной точки.

Однако определить окружность можно и многими другими способами. Приведем несколько примеров.
1. Окружность есть геометрическое место точек, сумма квадратов расстояний от которых до двух заданных точек постоянна и больше половины квадрата расстояния между этими точками.
2. Окружность есть геометрическое место точек, отношение расстояний от которых до двух данных точек А и В постоянно и не равно 1.

Такая окружность называется окружностью Аполлония точек А и В.
3. Окружность диаметра AB – это фигура, состоящая из точек A, B и всех точек плоскости, из которых отрезок AB виден под прямым углом.

Окружность обладает многими красивыми свойствами, доказательство которых не представляет труда. Сложнее определить, являются ли эти свойства также и признаками окружности, т.е. существуют ли другие кривые, обладающие ими. Перечислим сначала некоторые из свойств окружности, не присущие никаким другим кривым.
“Уникальные” свойства окружности
1. Два угла с вершинами на окружности, опирающиеся на одну и ту же дугу, равны.

2. Касательные к окружности, проведенные из одной точки, равны.

3. Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
4. Из всех замкнутых кривых, для которых длины всех хорд не превосходят заданной величины, окружность ограничивает область максимальной площади.
5. Любые две дуги окружности равной длины можно совместить.
Это свойство называется самоконгруэнтностью. На плоскости им, кроме окружности, обладает только прямая. Если кривая может не лежать в плоскости, оно задает также винтовую линию.

Однако замкнутых самоконгруэнтных кривых, отличных от окружности, не существует. Благодаря этому свойству меч, имеющий форму дуги окружности, можно вставлять и вынимать из ножен той же формы.
6. При любом расположении двух равных окружностей на плоскости они имеют не больше двух общих точек.

7. Любая прямая, проходящая через центр окружности, является ее осью симметрии.

Для некоторых из перечисленных свойств доказательства того, что они определяют окружность, а значит являются ее признаками, совсем элементарны. Для других, напротив, весьма сложны. Наиболее интересны доказательства признаков 2 и 6. (Попробуйте найти их самостоятельно; если не получится – смотрите ниже.)
А теперь приведем два красивых свойства окружности, которыми обладают и другие кривые.
“Не уникальные” свойства окружности
1. Окружность является кривой постоянной ширины.
Это значит, что если провести к окружности две параллельные касательные, то расстояние между ними не зависит от их направления.

Как ни странно, этим свойством обладают многие кривые, в том числе довольно сильно отличающиеся от окружности. Наиболее простая из них, так называемый треугольник Рело, изображена на следующем рисунке.
Он состоит из трех дуг окружностей, центры которых расположены в вершинах правильного треугольника, а радиусы равны его стороне. Если изготовить несколько катков, поперечные сечения которых являются кривыми постоянной ширины, то можно перевозить на них плоскую платформу, и она не будет перемещаться вверх и вниз.

Отметим также, что все кривые данной постоянной ширины имеют одну и ту же длину.
2. Любая прямая, которая делит пополам периметр окружности, делит пополам и площадь ограниченного ею круга.
Разумеется, помимо окружности этим свойством обладают любые кривые, имеющие центр симметрии. Гораздо интереснее то, что обладать им могут и не центрально-симметричные кривые, в том числе и выпуклые. Вот изображение одной из таких фигур:

Ее можно задать следующими уравнениями:
х = 12 · cos φ + cos 2φ + ½ · cos 4φ,
у = 12 · sin φ – sin 2φ + ½ · sin 4φ,
где φ меняется от до 2π.
Доказательство признака 2
Пусть дана выпуклая гладкая кривая, касательные к которой из любой точки равны. Возьмем произвольную точку А вне кривой и проведем касательные АВ’ и АС’. Докажем, что для всех точек А’, лежащих на дуге В’С’ (одной и той же), углы В’А’С’ совпадают.
Проведем через А’ касательную к кривой и найдем точки В и С ее пересечения с АС’ и АВ’.

По условию треугольники В’А’С’ и C’A’B’ равнобедренные, следовательно:
∠ BA’C’ = ½ · (π – ∠ CBA),
∠ CA’B’ = ½ · (π – ∠ ACB),
∠ C’A’B’ = π – ∠ BA’C’ – ∠ CA’B’ = ½ · (∠ CBA – ∠ ACB) = ½ · (π – ∠ BAC).
Таким образом угол, под которым видна хорда В’С’, не зависит от выбора точки на дуге. Для второй дуги доказательство аналогично. По первому признаку, из приведенных выше, кривая является окружностью.
Доказательство признака 6
Прежде всего, отметим, что в любую замкнутую кривую можно вписать правильный треугольник. Действительно, возьмем на кривой произвольную точку А и повернем кривую вокруг А на π/3. Точка пересечения старого и нового положения кривой, отличная от А будет второй вершиной треугольника.
Итак пусть правильный треугольник с центром О вписан в нашу кривую. Повернем ее вокруг О на угол 2π/3. Старое и новое положение кривой пересекаются, по крайней мере, в трех точках (вершинах треугольника) и, значит, совпадают, т.е. О является центром симметрии 3 порядка. Рассмотрим теперь поворот кривой вокруг О на произвольный угол φ. Если старое и новое положение кривой не совпадают, то число точек их пересечения кратно 3 (в силу симметрии) и не равно 0 (иначе одна кривая лежала бы целиком внутри другой, что для конгруэнтных кривых невозможно). Следовательно, кривая переходит в себя при любом повороте вокруг О, т.е. является окружностью.
Источники: А. Заславский. Свойства и признаки окружности. (“Квант”, №6, 2001), Википедия.
<<< Назад
Смотрите так же:
Окружность (справочные материалы)
Источник
Газзаева Ирина
Конспект занятия «Круг. Свойства круга»
Тема: Круг. Свойства круга
Цели: – Познакомить с кругом и его свойствами. Осваивать умения
соотносить сенсорные эталоны с предметами окружающего мира.
Продолжать формировать временные представления: закрепить
знания детей о времени года – осень. Закрепить понятие «столько же»
и умение различать цвета. Учить сравнивать круги по размеру с
помощью наложения, выявлять закономерность в расположении
фигур. Продолжать знакомить с множеством.
– Развивать воображение, ассоциативное мышление, учить
классифицировать и моделировать.
– Воспитывать любовь к природе, чувство коллективизма в труде, игре.
Материалы и оборудование
Демонстрационный: картинки с изображением овощей и фруктов круглой
формы.
Раздаточный: круги большие зеленого цвета и маленькие – красного цвета
(по количеству детей); для каждого ребенка 4 картинки с изображением
одного яблока на каждой картинке и карточка с изображением 4 корзинок.
Ход занятия
В. Дети, возьмите друг друга за руки и сделайте круг.
Мы стоим рука к руке,
Вместе мы – большая лента.
Можем мы большими быть,
Можем маленькими быть,
Но никто один не будет.
Мы все дружные ребята,
Помогаем друг другу,
И вместе нам интересно.
Дети поднимаются на
носки.
Дети приседают.
Дети встают,
идут по кругу и
останавливаются.
На демонстрационной доске картинки с изображением овощей и фруктов
круглой формы.
В. Дети, что вы видите на рисунках?
Ответы детей.
В. Яблоко какое?
Д. Круглое.
В. Помидор какой?
Д. Круглый.
В. Опишите пальчиком круг.
Дети за воспитателем пальчиком в воздухе описывают круг. Воспитатель
показывает зеленый и красный круги.
В. А у нас тоже есть круги. На что похож зелёный круг, а красный?
Д. На яблоко, на помидор.
Д/и «Разложи»
Воспитатель предлагает детям рассмотреть множество кругов: большие
зеленые и маленькие красные; обследовать круги: обвести их пальчиком,
покатать их, при этом сделать вывод, что круг хорошо катится, ему
ничто не мешает катиться.
Затем воспитатель предлагает сравнить по размеру круги (с помощью
наложения друг на друга) и выяснить, какие круги большие, а какие
маленькие.Разложить их в два обруча: большие – в один обруч, маленькие –
в другой обруч.
В. Теперь мы разложим фрукты. Сядем за столы.
Дети садятся за столы. На столах для каждого ребенка карточка с
изображением четырех корзинок и по 4 картинки – с изображением одного
яблока на каждой картинке.
В. Сколько корзинок?
Д. Много.
В. Сколько яблок?
Д. Много.
В. Положите в каждую корзинку по одному яблоку.
Дети выполняют задание.
В. В каждой корзинке есть яблоко?
Д. Да.
В. Сколько корзинок, столько и яблок. Повторите. Молодцы! Правильно
разложили яблоки в корзинки.
П/Д/и «Встаньте в круг»
На демонстрационной доске картинки с изображением овощей и фруктов
круглой формы.
В. Дети, что вы видите на рисунках?
Ответы детей.
В. Яблоко какое?
Д. Круглое.
В. Помидор какой?
Д. Круглый.
В. Опишите пальчиком круг.
Дети за воспитателем пальчиком в воздухе описывают круг. Воспитатель
показывает зеленый и красный круги.
В. А у нас тоже есть круги. На что похож зелёный круг, а красный?
Д. На яблоко, на помидор.
Д/и «Разложи»
Воспитатель предлагает детям рассмотреть множество кругов: большие
зеленые и маленькие красные; обследовать круги: обвести их пальчиком,
покатать их, при этом сделать вывод, что круг хорошо катится, ему
ничто не мешает катиться.
Затем воспитатель предлагает сравнить по размеру круги (с помощью
наложения друг на друга) и выяснить, какие круги большие, а какие
маленькие.Разложить их в два обруча: большие – в один обруч, маленькие –
в другой обруч.
В. Теперь мы разложим фрукты. Сядем за столы.
Дети садятся за столы. На столах для каждого ребенка карточка с
изображением четырех корзинок и по 4 картинки – с изображением одного
яблока на каждой картинке.
В. Сколько корзинок?
Д. Много.
В. Сколько яблок?
Д. Много.
В. Положите в каждую корзинку по одному яблоку.
Дети выполняют задание.
В. В каждой корзинке есть яблоко?
Д. Да.
В. Сколько корзинок, столько и яблок. Повторите. Молодцы! Правильно
разложили яблоки в корзинки.
П/Д/и «Встаньте в круг»
Воспитатель предлагает детям встать в круг.
Затем дети разбегаются и становятся в круг по сигналу воспитателя. Игра
повторяется 2-3 раза.
В. Какой большой красивый круг получился. А как сделать круг еще больше?
Д. Сделать шаги назад.
Дети делают шаг назад.
В. А как сделать круг меньше?
Д. Сделать шаги вперед.
В. Сделайте круг меньше.
Дети выполняют задание.
Итог
В. Сегодня вы познакомились с кругом. Какие фрукты и овощи круглой
формы вы знаете?
Ответы детей.
В. Молодцы!
Источник
