Какие свойства и характеристики определяют физические величины
Все объекты материального мира обладают рядом свойств, позволяющих отличать один объект от другого.
Свойство объекта – это объективная особенность, проявляющаяся при его создании, эксплуатации и потреблении.
Свойство объекта может быть выражено качественно – в виде словесного описания, и количественно – в виде графиков, цифр, диаграмм, таблиц.
Метрологическая наука занимается измерением количественных характеристик материальных объектов – физических величин.
Физическая величина – это свойство, в качественном отношении присущее многим объектам, а в количественном отношении индивидуально для каждого из них.
Например, массу имеют все материальные объекты, но у каждого из них величина массы индивидуальна.
Физические величины делятся на измеряемые и оцениваемые.
Измеряемые физические величины могут быть выражены количественно в виде определенного числа установленных единиц измерения.
Например, значение напряжения в сети составляет 220В.
Физические величины, которые не имеют единицы измерения, могут быть только оценены. Например, запах, вкус. Их оценка осуществляется дегустированием.
Некоторые величины можно оценить по шкале. Например: твердость материала – по шкале Викерса, Бринеля, Роквелла, силу землетрясения – по шкале Рихтера, температуру – по шкале Цельсия (Кельвина).
Физические величины можно квалифицировать по метрологическим признакам.
По видам явлений они делятся на
а) вещественные, описывающие физические и физико-химические свойства веществ, материалов и изделий из них.
Например, масса, плотность, электрическое сопротивление (для измерение сопротивления проводника по нему должен проходить ток, такое измерение называют пассивным).
б) энергетические, описывающие характеристики процессов преобразования, передачи и использования энергии.
К ним относятся: ток, напряжение, мощность, энергия. Эти физические величины называют активными. Они не требуют вспомогательного источника энергии.
Есть группа физических величин, которые характеризуют протекание процессов во времени, например, спектральные характеристики, корреляционные функции.
По принадлежности к различным группам физических процессов, величины могут быть
· пространственно-временные,
· механические,
· электрические,
· магнитные,
· тепловые,
· акустические,
· световые,
· физико-химические,
· ионизирующих излучений, атомной и ядерной физики.
По степени условной независимости физические величины делят на
· основные (независимые),
· производные (зависимые),
· дополнительные.
По наличию размерности физические величины делят на размерные и безразмерные.
Примером размерной величины является сила, безразмерной – уровень звуковой мощности.
Чтобы оценить количественно физическую величину вводится понятие размерфизической величины.
Размер физической величины – это количественная определенность физической величины, присущая конкретному материальному объекту, системе, процессу или явлению.
Например, каждое тело обладает определенной массой, следовательно, их можно различать по массе, т.е. по размеру физической величины.
Выражение размера физической величины в виде некоторого числа принятых для нее единиц определено как значение физической величины.
Значение физической величины – это выражение физической величины в виде некоторого числа принятых для нее единиц измерения.
Процесс измерения – это процедура сравнения неизвестной величины с известной физической величиной (сравниваемой) и в этой связи вводится понятие истинное значение физической величины.
Истинное значение физической величины – это значение физической величины, которое идеальным образом характеризует в качественном и количественном соотношении соответствующую физическую величину.
Истинное значение независимых физических величин воспроизведено в их эталонах.
Истинное значение применяют редко, больше пользуются действительным значением физической величины.
Действительное значение физической величины – это значение, полученное экспериментальным путем и несколько близкое к истинному значению.
Раньше было понятие «измеряемые параметры», сейчас по нормативному документу РМГ 29-99 рекомендуется понятие «измеряемые величины».
Физических величин много и их систематизируют. Система физических величин – это совокупность физических величин, образованная в соответствии с принятыми правилами, когда одни величины принимают за независимые, а другие определяют как функции независимых величин.
В названии системы физических величин применяют символы величин, принятые как основные.
Например, в механике, где в качестве основных приняты длина – L, масса – m и время – t, название системы соответственно – Lm t.
Система основных величин, соответствующих международной системе единиц СИ выражается символами LmtIKNJ, т.е. применены символы основных величин: длина – L, масса – М, время – t , сила тока – I, температура – K, количество вещества – N, сила света – J.
Основные физические величины не зависят от значений других величин этой системы.
Производная физическая величина – это физическая величина, входящая в систему величин и определяемая через основные величины этой системы. Например, сила определяется как масса на ускорение.
3. Единицы измерения физических величин.
Единицей измерений физической величины называется величина, которой по определению присвоено численное значение равное 1 и которая применяется для количественного выражения однородных с ней физических величин.
Единицы физических величин объединяют в систему. Первая система была предложена Гауссом К (миллиметр, миллиграмм, секунда). Сейчас действует система СИ, ранее был стандарт стран СЭВ.
Единицы измерений делятся на основные, дополнительные, производные и внесистемные.
В системе СИ семь основных единиц:
· длина (метр),
· масса (килограмм),
· время (секунда),
· термодинамическая температура (кельвин),
· количество вещества (моль),
· сила электрического тока (ампер),
· сила света (кандела).
Таблица 1
Обозначение основных единиц системы СИ
| Физическая величина | Единица измерений | |||
| Наименование | Обозна-чение | Наименование | Обозначение | |
| русское | международное | |||
| основные | ||||
| Длина | L | метр | м | m |
| Масса | m | килограмм | кг | kg |
| Время | t | секунда | с | s |
| Сила электрического тока | I | ампер | А | А |
| Термодинамическая температура | Т | кельвин | К | К |
| Количество вещества | n, v | моль | моль | mol |
| Cила света | J | кандела | кд | сd |
| дополнительные | ||||
| Плоский угол | – | радиан | рад | rad |
| Телесный угол | – | стерадиан | ср | sr |
Примечание. Радиан – это угол между двумя радиусами окружности, дуга между которыми по длине равна радиусу. В градусном исчислении радиан равен 57017’48’’.
Стерадиан – это телесный угол, вершина которого расположена в центре сферы и который вырезает на поверхности сферы площадь, равную площади квадрата со стороной по длине равной радиусу сферы. Измеряют телесный угол путем определения плоских углов и проведения дополнительных расчетов по формуле:
Q = 2p (1 – соsa/2),
где Q – телесный угол, a – плоский угол при вершине конуса, образованного внутри сферы данным телесным углом.
Телесному углу 1ср соответствует плоский угол, равный 65032’, углу p ср – плоский угол 1200, углу 2pср – 1800.
Дополнительные единицы СИ использованы для образования единиц угловой скорости, углового ускорения и некоторых других величин.
Сами по себе радиан и стерадиан применяются в основном для теоретических построений и расчетов, т.к. большинство важных для практики значений углов (полный угол, прямой угол и т.д.) в радианах выражаются трансцендентными числами (2p, p/2).
Производными называют единицы измерения, получаемые с помощью уравнений связи между физическими величинами. Например, единица сила в СИ – ньютон (Н):
Н = кг∙м/с2.
Несмотря на то, что система СИ универсальна, она разрешает применять некоторые внесистемные единицы, которые нашли широкое практическое применение (например, гектар).
Внесистемными называют единицы, не вошедшие ни в одну из общепринятых систем единиц физических величин.
Для многих практических случаев выбранные размеры физических величин неудобны – слишком малы или велики. Поэтому в практике измерений часто пользуются кратными и дольными единицами.
Кратной называется единица в целое число раз больше системной или внесистемной единицы. Например, кратная единица 1км = 1000 м.
Дольной называется единица, в целое число раз меньше системной или внесистемной единицы. Например, дольная единица 1 см = 0,01 м.
После принятия метрической системы мер была принята десятичная система образования кратных и дольных единиц, соответствующая десятичной системе нашего числового счета. Например, 106– мега, а 10-6 – микро.
Источник
1.2.1 Физические величины
Физическая величина – это характеристика одного из свойств физического объекта (явления или процесса), общая в качественном отношении многим объектам, но в количественном отношении индивидуальная для каждого объекта.
Значение физической величины – это оценка ее величины в виде некоторого числа принятых для нее единиц или числа по принятой для нее шкале.
Измерением физической величины называют совокупность операций, выполняемых с помощью технического средства, хранящего единицу или воспроизводящего шкалу физической величины, заключающихся в сравнении (в явном или неявном виде) измеряемой величины с ее единицей или шкалой с целью получения значения этой величины в форме, удобной для использования.
В теории измерений принято, в основном, пять типов шкал: наименования, порядка, интервалов, отношений и абсолютная.
Шкала наименования характеризуется только отношением эквивалентности. По своей сути она является качественной, не содержит пуля и единицы измерения (шкала оценки цвета).
Шкалы порядка характеризуются отношением эквивалентности ипорядка. Для практического использования такой шкалы необходимо установить ряд эталонов. Классификация объектов осуществляется сравнением интенсивности оцениваемого свойства с его эталонным значением (шкала землетрясений, шкала силы ветра, шкала твердости тел и т.п.).
Шкала разностей характеризуется тем, что к отношениям эквивалентности и порядка добавляется эквивалентность интервалов (разностей) между различными качественными проявлениями свойства. Она имеет условные нулевые значения, а величина интервалов устанавливается по согласованию (шкала интервалов времени).
Шкалы отношений описывают свойства, к которым применимы отношения эквивалентности, порядка и суммирования (вычитания, умножения). Эти шкалы имеют естественное нулевое значение, а единицыизмерений устанавливаются по согласованию. Для шкалы отношений достаточно одного эталона, чтобы распределить все исследуемые объекты по интенсивности измеряемого свойства (шкала массы).
Абсолютные шкалы обладают всеми признаками шкал отношений, но дополнительно в них существует естественное однозначное определение единицы измерения. Такие шкалы соответствуют относительным величинам (отношениям одноименных физических величин, описываемых шкалами отношений). Среди них выделяются абсолютные шкалы, значения которых находятся в пределах от 0 до 1 (КПД).
Практическая реализация шкал конкретных свойств достигается путем стандартизации единиц измерений, шкал и (или) способов и условий их однозначного воспроизведения.
Из всего разнообразия физических величин можно выделить три вида величин, измерение которых осуществляется по различным правилам,
К первому виду относятся физические величины, на множестве размеров которых определены лишь отношения порядка и эквивалентности («мягче», «тверже», «теплее», «холоднее» и т.д.).
Для второго вида физических величин отношение порядка и эквивалентности имеет место как между размерами, так и между разностями в парах их размеров. Так, разности интервалов времени считаются раины ми, если расстояния между соответствующими отметками равны.
Третий вид составляют аддитивные физические величины. Это величины, на множестве размеров которых определены не только отношении порядка и эквивалентности, но операции сложения и вычитания. К таким величинам относятся длина, масса, сила тока и др. Их можно измерять по частям, а также воспроизводить с помощью многозначной меры, основанной на суммировании отдельных мер (сумма масс двух тел – это масса такого тела, которое уравновешивает на равноплечих весах первые два).
1.2.2 Понятие о системе физических величин
Система физических величин – это совокупность взаимосвязанных физических величин, образованная в соответствии с принятыми принципами, когда одни величины принимаются за независимые, а другие являются функциями независимых величин. Система содержит основные физические величины, условно принятые в качестве независимых от других величин этой системы, и производные физические величины, определяемые через основные величины этой системы и образованные с помощью уравнений, связывающих их с основными величинами.
Единица физической величины – физическая величина фиксированного размера, которой условно присвоено значение, равное единице, и которая применяется для количественного выражения однородных физических величин.
Размерность физической величины – выражение в форме степенного одночлена, составленного из произведений символов основных физических величин в различных степенях, которое отражает связь данной величины с основными физическими величинами, принятыми в данной системе, с коэффициентом пропорциональности, равным единице.
Размерность величин обозначают знаком dim.
Например, dimX = Ll• Мт•Тt
где L,М ,Т — символы величин длины, массы, времени, принятые за основные;
l ,m ,t– показатели размерности основных величин, которые могут быть целыми или дробными, положительными или отрицательными вещественными числами.
Показатель размерности физической величины – показатель степени, в которую возведена размерность основной физической величины, входящей в размерность производной физической величины.
Источник
Качество измерений
Без измерений не может обойтись ни одна наука, поэтому метрология как наука об измерениях находится в тесной связи со всеми другими науками. Поэтому, основное понятие метрологии – измерение. Согласно ГОСТ 16263 – 70, измерение – это нахождение значения физической величины (ФВ) опытным путем с помощью специальных технических средств.
Возможность измерения обуславливается предварительным изучением заданного свойства объекта измерений, построением абстрактных моделей как самого свойства, так и его носителя – объекта измерения в целом. Поэтому, место измерения определяется среди методов познания, обеспечивающих достоверность измерения. С помощью метрологических процедур решаются задачи формирования данных (фиксации результатов познания). Измерение с этой точки зрения представляет собой метод кодирования сведений и регистрации полученной информации.
Измерения обеспечивают получение количественной информации об объекте управления или контроля, без которой невозможно точное воспроизведение всех заданных условий технического процесса, обеспечение высокого качества изделий и эффективного управления объектом. Все это составляет технический аспект измерений.
До 1918 г. метрическая система внедрялась в России факультативно, наряду со старой русской и английской (дюймовой) системами. Значительные изменения в метрологической деятельности стали происходить после подписания Советом народных комиссаров РСФСР декрета “О введении международной метрической системы мер и весов”. Внедрение метрической системы в России происходило с 1918 по 1927 г. После Великой Отечественной войны и до сего времени метрологическая работа в нашей стране проводится под руководством Государственного комитета по стандартам (Госстандарт).
В 1960 г. ХI Международная конференция по мерам и весам приняла Международную систему единиц ФВ – систему СИ. Сегодня метрическая система узаконена более чем в 124 странах мира.
В настоящее время на базе Главной палаты мер и весов существует высшее научное учреждение страны – Всероссийский научно-исследовательский институт метрологии им. Д.И. Менделеева (ВНИИМ). В лабораториях института разрабатываются и хранятся государственные эталоны единиц измерений, определяются физические константы и свойства веществ и материалов. Тематика работ института охватывает линейные, угловые, оптические и фотометрические, акустические, электрические и магнитные измерения, измерения массы, плотности, силы, давления, вязкости, твердости, скорости, ускорения и ряда других величин.
В 1955 г. под Москвой был создан второй метрологический центр страны – ныне Всероссийский научно-исследовательский институт физико-технических и радиотехнических измерений (ВНИИФТРИ). Он разрабатывает эталоны и средства точных измерений в ряде важнейших областей науки и техники: радиоэлектронике, службе времени и частоты, акустике, атомной физике, физике низких температур и высоких давлений.
Третьим метрологическим центром России является Всероссийский научно-исследовательский институт метрологической службы (ВНИИМС) – головная организация в области прикладной и законодательной метрологии. На него возложена координация и научно-методическое руководство метрологической службой страны. Кроме перечисленных существует ряд региональных метрологических институтов и центров.
К международным метрологическим организациям относится и Международная организация законодательной метрологии (МОЗМ), образованная в 1956 г. При МОЗМ в Париже работает Международное бюро законодательной метрологии. Его деятельностью руководит Международный комитет законодательной метрологии. Некоторые вопросы метрологии решает Международная организация по стандартизации (ИСО).
Физические свойства и величины. Классификация физических величин.
Шкалы измерений
Все объекты окружающего мира характеризуются своими свойствами.
Свойство – философская категория, выражающая такую сторону объекта (явления или процесса), которая обусловливает его различие или общность с другими объектами, и обнаруживается в его отношениях к ним. Свойство – категория качественная. Для количественного описания различных свойств физических тел, явлений и процессов вводится понятие величины.
Величина – это мера объекта (явления, процесса или чего-либо другого), мера того, что может быть выделено среди других свойств и оценено тем или иным способом, в том числе и количественно. Величина не существует сама по себе, она имеет место лишь постольку, поскольку существует объект со свойствами, выраженными данной величиной.
Таким образом, понятие величина, это понятие большей общности, чем качество (свойство, атрибут) и количество.
Физические свойства и величины
Существует два вида величин: реальные и идеальные.
Идеальные величины (числовые значения величин, графики, функции, операторы и т.п.) главным образом относятся к математике и являются обобщением (математической моделью) конкретных реальных понятий. Они вычисляются тем или иным способом.
Реальные величины, в свою очередь, подразделяются, как физические и нефизические. При этом, физическая величина в общем случае может быть определена как величина, свойственная материальным объектам (телам, процессам, явлениям), изучаемым в естественных (физика, химия) и технических науках. К нефизическим величинам следует отнести величины, присущие общественным (нефизическим) наукам – философии, социологии, экономике и т.п.
Стандарт ГОСТ 16263-70 трактует физическую величину, как численное выражение конкретного свойства физического объекта, в качественном отношении общее для многих физических объектов, а в количественном, абсолютно индивидуальное для каждого из них. Индивидуальность в количественном отношении здесь понимается в том смысле, что свойство может быть для одного объекта больше, в определенное число раз, или меньше, чем для другого.
Таким образом, физические величины – это измеренные свойства физических объектов или процессов, с помощью которых они могут быть изучены.
Физические величины (ФВ) целесообразно дополнительно классифицировать, как измеряемые и оцениваемые.
Измеряемые физические величины могут быть выражены количественно в виде определенного числа установленных единиц измерения. Возможность введения и использования единиц измерения, является важным отличительным признаком измеряемых ФВ.
Физические величины, для которых по тем или иным причинам не может быть введена единица измерения, могут быть только оценены. Под оцениваниемв таком случае понимается операция приписывания данной величине определенного числа, проводимая по установленным правилам. Оценивание величины осуществляется при помощи шкал.
Нефизические величины, для которых единицы измерения и шкалы в принципе не может быть введены, могут быть только оценены.
Классификация физических величин
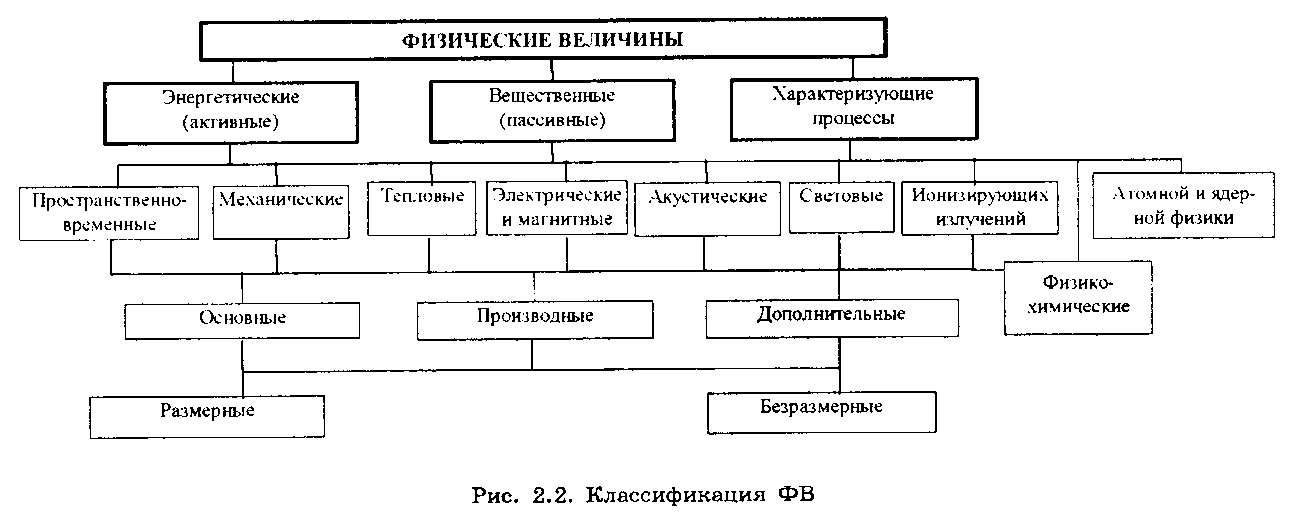
Для более детального изучения ФВ необходимо их классифицировать, выявив общие метрологические особенности их отдельных групп. Возможные классификации ФВ показаны на рис. 2.2.
По видам явлений они делятся на следующие группы:
· вещественные, т.е. описывающие физические и физико-химические свойства веществ, материалов и изделий из них. К этой группе относятся масса, плотность, электрическое сопротивление, емкость, индуктивность и др. Иногда указанные ФВ называют пассивными. Для их измерения необходимо использовать вспомогательный источник энергии, с помощью которого формируется сигнал измерительной информации. При этом пассивные ФВ преобразуются в активные, которые и измеряются;
· энергетические, т.е. величины, описывающие энергетические характеристики процессов преобразования, передачи и использования энергии. К ним относятся ток, напряжение, мощность, энергия. Эти величины называют активными. Они могут быть преобразованы в сигналы измерительной информации без использования вспомогательных источников энергии;
· 
характеризующие протекание процессов во времени. К этой группе относятся различного вида спектральные характеристики, корреляционные функции и др.
По принадлежности к различным группам физических процессов ФВ делятся на пространственно-временные, механические, тепловые, электрические и магнитные, акустические, световые, физико-химические, ионизирующих излучений, атомной и ядерной физики.
По степени условной независимости от других величин данной группы ФВ делятся на основные (условно независимые), производные (условно зависимые) и дополнительные. В настоящее время в системе СИ используется семь физических величин, выбранных в качестве основных: длина, время, масса, температура, сила электрического тока, сила света и количества вещества. К дополнительным физическим величинам относятся плоский и телесный углы.
По наличию размерности ФВ делятся на размерные, т.е. имеющие размерность, и безразмерные.
Физические объекты обладают неограниченным числом свойств, которые проявляются с бесконечным разнообразием. Это затрудняет их отражение совокупностями чисел с ограниченной разрядностью, возникающее при их измерении. Среди множества специфических проявлений свойств есть и несколько общих. Н.Р. Кэмпбелл установил для всего разнообразия свойств Х физического объекта наличие трех наиболее общих проявлений в отношениях эквивалентности, порядка и аддитивности. Эти отношения в математической логике аналитически описываются простейшими постулатами.
При сравнении величин выявляется отношение порядка (больше, меньше или равно), т.е. определяется соотношение между величинами. Примерами интенсивных величин являются твердость материала, запах и др.
Интенсивные величины могут быть обнаружены, классифицированы по интенсивности, подвергнуты контролю, количественно оценены монотонно возрастающими или убывающими числами.
На основании понятия “интенсивная величина” вводятся понятия физической величины и ее размера. Размер физической величины – количественное содержание в данном объекте свойства, соответствующего понятию ФВ.
Шкалы измерений
В практической деятельности необходимо проводить измерения различных физических величин, характеризующих свойства тел, веществ, явлений и процессов. Некоторые свойства проявляются только качественно, другие – количественно. Разнообразные проявления (количественные или качественные) того, или иного свойства объекта исследования, образуют множество, отображения элементов которого на упорядоченное множество чисел, или, в, более общем случае, условных знаков, образуют шкалу измерения этого свойства. Шкала измерений количественного свойства конкретной физической величины является шкалой этой физической величины. Таким образом, шкала физической величины – это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений. Термины и определения теории шкал измерений изложены в документе МИ 2365-96.
В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.
1. Шкала наименований (шкала классификации). Такие шкалы используются для классификации эмпирических объектов, свойства которых проявляются только в отношении эквивалентности. Эти свойства нельзя считать физическими величинами, поэтому шкалы такого вида не являются шкалами ФВ. Это самый простой тип шкал, основанный на приписывании качественным свойствам объектов чисел, играющих роль имен. В шкалах наименований, в которых отнесение отражаемого свойства к тому или иному классу эквивалентности осуществляется с использованием органов чувств человека, наиболее адекватен результат, выбранный большинством экспертов. При этом большое значение имеет правильный выбор классов эквивалентной шкалы – они должны надежно различаться наблюдателями, экспертами, оценивающими данное свойство. Нумерация объектов по шкале наименований осуществляется по принципу: “не приписывай одну и ту же цифру разным объектам”. Числа, приписанные объектам, могут быть использованы для определения вероятности или частоты появления данного объекта, но их нельзя использовать для суммирования и других математических операций.
Поскольку данные шкалы характеризуются только отношениями эквивалентности, то в них отсутствует понятия нуля, “больше” или “меньше” и единицы измерения. Примером шкал наименований являются широко распространенные атласы цветов, предназначенные для идентификации цвета.
2. Шкала порядка (шкала рангов). Если свойство данного эмпирического объекта проявляет себя в отношении эквивалентности и порядка по возрастанию или убыванию количественного проявления свойства, то для него может быть построена шкала порядка. Она является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство. В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.
В случаях, когда уровень познания явления не позволяет точно установить отношения, существующие между величинами данной характеристики, либо применение шкалы удобно и достаточно для практики, используют условные (эмпирические) шкалы порядка. Условная шкала – это шкала ФВ, исходные значения которой выражены в условных единицах. Например, шкала вязкости Энглера, 12-бальная шкала Бофорта для силы морского ветра.
Широкое распространение получили шкалы порядка с нанесенными на них реперными точками. К таким шкалам, например, относится шкала Мооса для определения твердости минералов, которая содержит 10 опорных (реперных) минералов с различными условными числами твердости: тальк – 1; гипс – 2; кальций – 3; флюорит – 4; апатит – 5; ортоклаз – 6; кварц – 7; топаз – 8; корунд – 9; алмаз – 10. Отнесение минерала к той или иной градации твердости осуществляется на основании эксперимента, который состоит в том, что испытуемый материал царапается опорным. Если после царапанья .испытуемого минерала кварцем (7) на нем остается след, а после ортоклаза (6) – не остается, то твердость испытуемого материала составляет более б, но менее 7. Более точного ответа в этом случае дать невозможно.
В условных шкалах одинаковым интервалам между размерами данной величины не соответствуют одинаковые размерности чисел, отображающих размеры. С помощью этих чисел можно найти вероятности, моды, медианы, квантили, однако их нельзя использовать для суммирования, умножения и других математических операций.
Определение значения величин при помощи шкал порядка нельзя считать измерением, так как на этих шкалах не могут быть введены единицы измерения. Операцию по приписыванию числа требуемой величине следует считать оцениванием. Оценивание по шкалам порядка является неоднозначным и весьма условным, о чем свидетельствует рассмотренный пример.
3. Шкала интервалов (шкала разностей). Эти шкалы являются дальнейшим развитием шкал порядка и применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало – нулевую точку. К таким шкалам относится летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.
На шкале интервалов определены действия сложения и вычитания интервалов. Действительно, по шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.
4. Шкала отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода – аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода – пропорциональные). Их примерами являются шкала массы (второго рода), термодинамической температуры (первого рода).
В шкалах отношений существует однозначный естественный критерий нулевого количественного проявления свойства и единица измерений, установленная по соглашению. С формальной точки зрения шкала отношений является шкалой интервалов с естественным началом отсчета. К значениям, полученным по этой шкале, применимы все арифметические действия, что имеет важное значение при измерении ФВ.
Шкалы отношений – самые совершенные. Они описываются уравнением 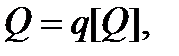 , где Q – ФВ, для которой строится шкала, [Q] – ее единица измерения, q – числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1[Q1]/[Q2].
, где Q – ФВ, для которой строится шкала, [Q] – ее единица измерения, q – числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q2 = q1[Q1]/[Q2].
5. Абсолютные шкалы. Некоторые авторы используют понятие абсолютных шкал, под которыми понимают шкалы, обладающие всеми признаками шкал отношений, но дополнительно имеющие естественное однозначное определение единицы измерения и не зависящие от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.
Отметим, что шкалы наименований и порядка называют неметрическими (концептуальными), а шкалы интервалов и отношений – метрическими (материальными). Абсолютные и метрические шкалы относятся к разряду линейных. Практическая реализация шкал измерений осуществляется путем стандартизации как самих шкал и единиц измерений, так и, в необходимых случаях, способов и условий их однозначного воспроизведения.
Источник
