Какие свойства характеризуют сопротивление материала деформации
Механические свойства материалов, совокупность показателей, характеризующих сопротивление материала воз действующей на него нагрузке, его способность деформироваться при этом, а также особенности его поведения в процессе разрушения. В соответствии с этим М. с. м. измеряют напряжениями (обычно в кгс/мм2 или Мн/м2), деформациями (в %), удельной работой деформации и разрушения (обычно в кгс×м/см2 или Мдж/м2), скоростью развития процесса разрушения при статической или повторной нагрузке (чаще всего в мм за 1 сек или за 1000 циклов повторений нагрузки, мм/кцикл). М. с. м. определяются при механических испытаниях образцов различной формы.
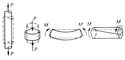
В общем случае материалы в конструкциях могут подвергаться самым различным по характеру нагрузкам (рис. 1): работать на растяжение, сжатие, изгиб, кручение, срез и т. д. или подвергаться совместному действию нескольких видов нагрузки, например растяжению и изгибу. Также разнообразны условия эксплуатации материалов и по температуре, окружающей среде, скорости приложения нагрузки и закону её изменения во времени. В соответствии с этим имеется много показателей М. с. м. и много методов механических испытаний. Для металлов и конструкционных пластмасс наиболее распространены испытания на растяжение, твёрдость, ударный изгиб; хрупкие конструкционные материалы (например, керамику, металлокерамику) часто испытывают на сжатие и статический изгиб; механические свойства композиционных материалов важно оценивать, кроме того, при испытаниях на сдвиг.
Диаграмма деформации. Приложенная к образцу нагрузка вызывает его деформацию. Соотношения между нагрузкой и деформацией описываются т. н. диаграммой деформации (рис. 2). Вначале деформация образца (при растяжении — приращение длины Dl ) пропорциональна возрастающей нагрузке Р, затем в точке n эта пропорциональность нарушается, однако для увеличения деформации необходимо дальнейшее повышение нагрузки Р; при Dl > Dlв деформация развивается без приложения усилия извне, при постепенно падающей нагрузке. Вид диаграммы деформации не меняется, если по оси ординат откладывать напряжение
а по оси абсцисс — относительное удлинение
(F0 и l0 — соответственно начальная площадь поперечного сечения и расчётная длина образца).
Сопротивление материалов измеряется напряжениями, характеризующими нагрузку, приходящуюся на единицу площади поперечного сечения образца
в кгс/мм2. Напряжение
при котором нарушается пропорциональный нагрузке рост деформации, называется пределом пропорциональности. При нагрузке Р < Рn разгрузка образца приводит к исчезновению деформации, возникшей в нём под действием приложенного усилия; такая деформация называется упругой. Небольшое превышение нагрузки относительно Рn может не изменить характера деформации — она по-прежнему сохранит упругий характер. Наибольшая нагрузка, которую выдерживает образец без появления остаточной пластической деформации при разгрузке, определяет предел упругости материала:
У конструкционных неметаллический материалов (пластмассы, резины) приложенная нагрузка может вызвать упругую, высокоэластическую и остаточную деформации. В отличие от упругой, высокоэластическая деформация исчезает не сразу после разгрузки, а с течением времени. Высокопрочные армированные полимеры (стеклопластики, углепластики и др.) разрушаются при удлинении 1—3%. На последних стадиях нагружения у некоторых армированных полимеров появляется высокоэластическая деформация. Высокоэластический модуль ниже модуля упругости, поэтому диаграмма деформации в этом случае имеет тенденцию отклоняться к оси абсцисс.
Упругие свойства. В упругой области напряжение и деформация связаны коэффициентом пропорциональности. При растяжении s = Еd, где Е — т. н. модуль нормальной упругости, численно равный тангенсу угла наклона прямолинейного участка кривой s = s(d) к оси деформации (рис. 2). При испытании на растяжение цилиндрического или плоского образца одноосному (s1>0; (s2 = s3 = 0) напряжённому состоянию соответствует трёхосное деформированное состояние (приращение длины в направлении действия приложенных сил и уменьшение линейных размеров в двух других взаимно перпендикулярных направлениях): d1>0; d2 = d3 < 0. Соотношение между поперечной и продольной деформацией (коэффициент Пуассона)
в пределах упругости для основных конструкционных материалов колеблется в довольно узких пределах (0,27—0,3 для сталей, 0,3—0,33 для алюминиевых сплавов). Коэффициент Пуассона является одной из основных расчётных характеристик. Зная m и Е, можно расчётным путём определить и модуль сдвига
и модуль объёмной упругости
Для определения Е, G, и m пользуются тензометрами.
Сопротивление пластической деформации. При нагрузках Р > Рв наряду со всё возрастающей упругой деформацией появляется заметная необратимая, не исчезающая при разгрузке пластическая деформация. Напряжение, при котором остаточная относительная деформация (при растяжении — удлинение) достигает заданной величины (по ГОСТ — 0,2 %), называется условным пределом текучести и обозначается
Практически точность современных методов испытания такова, что sп и sе определяют с заданными допусками соответственно на отклонение от закона пропорциональности [увеличение ctg(90 — a) на 25—50 %] и на величину остаточной деформации (0,003—0,05 %) и говорят об условных пределах пропорциональности и упругости. Кривая растяжения конструкционных металлов может иметь максимум (точка в на рис. 2) или обрываться при достижении наибольшей нагрузки Рв’. Отношение
характеризует временное сопротивление (предел прочности) материала. При наличии максимума на кривой растяжения в области нагрузок, лежащих на кривой левее в, образец деформируется равномерно по всей расчётной длине l0, постепенно уменьшаясь в диаметре, но сохраняя начальную цилиндрическую или призматическую форму. При пластической деформации металлы упрочняются, поэтому, несмотря на уменьшение сечения образца, для дальнейшей деформации требуется прикладывать всё возрастающую нагрузку. sв, как и условные s0,2, sn и sе, характеризует сопротивление металлов пластической деформации. На участке диаграммы деформации правее в форма растягиваемого образца изменяется: наступает период сосредоточенной деформации, выражающейся в появлении «шейки». Уменьшение сечения в шейке «обгоняет» упрочнение металлов, что и обусловливает падение внешней нагрузки на участке Рв — Pk.
У многих конструкционных материалов сопротивление пластической деформации в упруго-пластической области при растяжении и сжатии практически одинаково. Для некоторых металлов и сплавов (например, магниевые сплавы, высокопрочные стали) характерны заметные различия по этой характеристике при растяжении и сжатии. Сопротивление пластической деформации особенно часто (при контроле качества продукции, стандартности режимов термической обработки и в др. случаях) оценивается по результатам испытаний на твёрдость путём вдавливания твёрдого наконечника в форме шарика (твёрдость по Бринеллю или Роквеллу), конуса (твёрдость по Роквеллу) или пирамиды (твёрдость по Виккерсу). Испытания на твёрдость не требуют нарушения целостности детали и потому являются самым массовым средством контроля механических свойств. Твёрдость по Бринеллю (HB) при вдавливании шарика диаметром D под нагрузкой Р характеризует среднее сжимающее напряжение, условно вычисляемое на единицу поверхности шарового отпечатка диаметром d:
Характеристики пластичности. Пластичность при растяжении конструкционных материалов оценивается удлинением
или сужением
при сжатии — укорочением
(где h0 и hk — начальная и конечная высота образца), при кручении — предельным углом закручивания рабочей части образца Q, рад или относительным сдвигом g = Qr (где r — радиус образца). Конечная ордината диаграммы деформации (точка k на рис. 2) характеризует сопротивление разрушению металла Sk, которое определяется
(Fk — фактическая площадь в месте разрыва).
Характеристики разрушения. Разрушение происходит не мгновенно (в точке k), а развивается во времени, причём начало в разрушения может соответствовать какой-то промежуточной точке на участке вк, а весь процесс заканчиваться при постепенно падающей до нуля нагрузке. Положение точки к на диаграмме деформации в значительной степени определяется жёсткостью испытательной машины и иннерционностью измерительной системы. Это делает величину Sk в большой мере условной.
Многие конструкционные металлы (стали, в том числе высокопрочные, жаропрочные хромоникелевые сплавы, мягкие алюминиевые сплавы и др.) разрушаются при растяжении после значительной пластической деформации с образованием шейки. Часто (например, у высокопрочных алюминиевых сплавов) поверхность разрушения располагается под углом примерно 45° к направлению растягивающего усилия. При определенных условиях (например, при испытании хладноломких сталей в жидком азоте или водороде, при воздействии растягивающих напряжений и коррозионной среды для металлов, склонных к коррозии под напряжением) разрушение происходит по сечениям, перпендикулярным растягивающей силе (прямой излом), без макропластической деформации.
Прочность материалов, реализуемая в элементах конструкций, зависит не только от механических свойств самого металла, но и от формы и размеров детали (т. н. эффекты формы и масштаба), упругой энергии, накопленной в нагруженной конструкции, характера действующей нагрузки (статическая, динамическая, периодически изменяющаяся по величине), схемы приложения внешних сил (растяжение одноосное, двухосное, с наложением изгиба и др.), рабочей температуры, окружающей среды. Зависимость прочности и пластичности металлов от формы характеризуется т. н. чувствительностью к надрезу, оцениваемой обычно по отношению пределов прочности надрезанного и гладкого образцов
(у цилиндрических образцов надрез обычно выполняют в виде круговой выточки, у полос — в виде центрального отверстия или боковых вырезов). Для многих конструкционных материалов это отношение при статической нагрузке больше единицы, что связано со значительной местной пластической деформацией в вершине надреза. Чем острее надрез, тем меньше локальная пластическая деформация и тем больше доля прямого излома в разрушенном сечении. Хорошо развитый прямой излом можно получить при комнатной температуре у большинства конструкционных материалов в лабораторных условиях, если растяжению или изгибу подвергать образцы массивного сечения (тем толще, чем пластичнее материал), снабдив эти образцы специальной узкой прорезью с искусственно созданной трещиной (рис. 3). При растяжении широкого, плоского образца пластическая деформация затруднена и ограничивается небольшой областью размером 2ry (на рис. 3, б заштрихована), непосредственно примыкающей к кончику трещины. Прямой излом обычно характерен для эксплуатационных разрушений элементов конструкций.
Широкое распространение получили предложенные американским учёным Дж. Р. Ирвином в качестве констант для условий хрупкого разрушения такие показатели, как критический коэффициент интенсивности напряжений при плоской деформации K1C и вязкость разрушения
При этом процесс разрушения рассматривается во времени и показатели K1C(G1C) относятся к тому критическому моменту, когда нарушается устойчивое развитие трещины; трещина становится неустойчивой и распространяется самопроизвольно, когда энергия, необходимая для увеличения её длины, меньше энергии упругой деформации, поступающей к вершине трещины из соседних упруго напряжённых зон металла.
При назначении толщины образца t и размеров трещины 2lтр исходят из следующего требования
Коэффициент интенсивности напряжений К учитывает не только значение нагрузки, но и длину движущейся трещины:
(l учитывает геометрию трещины и образца), выражается в кгс/мм3/2 или Мн/м3/2. По K1C или G1C можно судить о склонности конструкционных материалов к хрупкому разрушению в условиях эксплуатации.
Для оценки качества металла весьма распространены испытания на ударный о изгиб призматических образцов, имеющих на одной стороне надрез. При этом оценивают ударную вязкость (в кгс×м/см2 или Мдж/м2) — работу деформации и разрушения образца, условно отнесённую к поперечному сечению в месте надреза. Широкое распространение получили испытания на ударный изгиб образцов с искусственно полученной в основании надреза трещиной усталости. Работа разрушения таких образцов ату находится в целом в удовлетворительном соответствии с такой характеристикой разрушения, как K1C, и ещё лучше с отношением
Временная зависимость прочности. С увеличением времени действия нагрузки сопротивление пластической деформации и сопротивление разрушению понижаются. При комнатной температуре у металлов это становится особенно заметным при воздействии коррозионной (коррозия под напряжением) или др. активной (эффект Ребиндера) среды. При высоких температурах наблюдается явление ползучести, т. е. прироста пластической деформации с течением времени при постоянном напряжении (рис. 4, а). Сопротивление металлов ползучести оценивают условным пределом ползучести — чаще всего напряжением, при котором пластическая деформация за 100 ч достигает 0,2 %, и обозначают его s0,2/100. Чем выше температура t, тем сильнее выражено явление ползучести и тем больше снижается во времени сопротивление разрушению металла (рис. 4, б). Последнее свойство характеризуют т. н. пределом длительной прочности, т. е. напряжением, которое при данной температуре вызывает разрушение материала за заданное время (например, st100, st1000 и т. д.). У полимерных материалов температурно-временная зависимость прочности и деформации выражена сильнее, чем у металлов. При нагреве пластмасс наблюдается высокоэластическая обратимая деформация; начиная с некоторой более высокой температуры развивается необратимая деформация, связанная с переходом материала в вязкотекучее состояние. С ползучестью связано и др. важное механическое свойство материалов — склонность к релаксации напряжений, т. е. к постепенному падению напряжения в условиях, когда общая (упругая и пластическая) деформация сохраняет постоянную заданную величину (например, в затянутых болтах). Релаксация напряжений обусловлена увеличением доли пластической составляющей общей деформации и уменьшением её упругой части.
Если на металл действует нагрузка, периодически меняющаяся по какому-либо закону (например, синусоидальному), то с увеличением числа циклов N нагрузки его прочность уменьшается (рис. 4, в) — металл «устаёт». Для конструкционной стали такое падение прочности наблюдается до N = (2—5) ×106 циклов. В соответствии с этим говорят о пределе усталости конструкционной стали, понимая под ним обычно амплитуду напряжения
ниже которой сталь при повторно-переменной нагрузке не разрушается. При |smin| = |smax| предел усталости обозначают символом s-1. Кривые усталости алюминиевых, титановых и магниевых сплавов обычно не имеют горизонтального участка, поэтому сопротивление усталости этих сплавов характеризуют т. н. ограниченными (соответствующими заданному N) пределами усталости. Сопротивление усталости зависит также от частоты приложения нагрузки. Сопротивление материалов в условиях низкой частоты и высоких значений повторной нагрузки (медленная, или малоцикловая, усталость) не связано однозначно с пределами усталости. В отличие от статической нагрузки, при повторно-переменных нагрузках всегда проявляется чувствительность к надрезу, т. е. предел усталости при наличии надреза ниже предела усталости гладкого образца. Для удобства чувствительность к надрезу при усталости выражают отношением
характеризует асимметрию цикла). В процессе уставания можно выделить период, предшествующий образованию очага усталостного разрушения, и следующий за ним, иногда довольно длительный, период развития трещины усталости. Чем медленнее развивается трещина, тем надёжнее работает материал в конструкции. Скорость развития трещины усталости dl/dN связывают с коэффициентом интенсивности напряжений степенной функцией:
Различают сопротивление термической усталости, когда появляющиеся в материале напряжения обусловлены тем, что в силу тех или иных причин, например из-за формы детали или условий её закрепления, возникающие при циклическом изменении температуры тепловые перемещения не могут быть реализованы. Сопротивление термической усталости зависит и от многих других свойств материала — коэффициентов линейного расширения и температуропроводности, модуля упругости, предела упругости и др.
Лит.: Давиденков Н. Н., Динамические испытания металлов, 2 изд., Л. — М., 1936; Ратнер С. И., Разрушение при повторных нагрузках, М., 1959; Серенсен С. В., Когаев В. П., Шнейдерович Р. М., Несущая способность и расчеты деталей машин на прочность, 2 изд., М., 1963; Прикладные вопросы вязкости разрушения, пер. с англ., М., 1968; Фридман Я. Б., Механические свойства металлов, 3 изд., М., 1974; Методы испытания, контроля и исследования машиностроительных материалов, под ред. А. Т. Туманова, т. 2, М., 1974.
С. И. Кишкина.

Рис. 4. Изменение механических свойств конструкционных материалов в функции времени (или числа циклов).
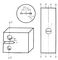
Рис. 3. Образец со специально созданной в вершине надреза трещиной усталости для определения K1C. Испытания на внецентренное (а) и осевое (б) растяжение.

Рис. 1. Схемы деформации при разных способах нагружения: а — растяжение, б — сжатие, в — изгиб, г — кручение (пунктиром показана начальная форма образцов).
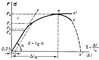
Рис. 2. Типичная диаграмма деформации при растяжении конструкционных металлов.
Оглавление БСЭ
Источник
МЕХАНИЧЕСКИЕ СВОЙСТВА МАТЕРИАЛОВ
Критерии выбора материала
Свойства – это количественная или качественная характеристика материала, определяющая его общность или различие с другими материалами.
Выделяют три основные группы свойств: эксплуатационные, технологические и стоимостные, которые лежат в основе выбора материала и определяют техническую и экономическую целесообразность его применения. Первостепенное значение имеют эксплуатационные свойства.
Эксплуатационными называют свойства материала, которые определяют работоспособность деталей машин, приборов и инструментов, их силовые, скоростные, стоимостные и другие технико-эксплуатационные показатели.
Работоспособность подавляющего большинства деталей машин и изделий обеспечивает уровень механических свойств, которые характеризуют поведение материала под действием внешней нагрузки. Так как условия нагружения деталей машин разнообразны, то механические свойства включают большую группу показателей.
В зависимости от изменения во времени нагрузки подразделяют на статические и динамические. Статическое нагружение характеризуется малой скоростью изменения своей величины, а динамические нагрузки изменяются во времени с большими скоростями, например, при ударном нагружении. Кроме того, нагрузки подразделяют на растягивающие, сжимающие, изгибающие, скручивающие и срезывающие. Изменение нагрузки может иметь периодически повторяющийся характер, вследствие чего их называют повторно- переменными или циклическими. В условиях эксплуатации машин воздействие перечисленных нагрузок может проявляться в различных сочетаниях.
Под воздействием внешних нагрузок, а также структурно-фазовых превращений в материале конструкций возникают внутренние силы, которые могут быть выражены через внешние нагрузки. Внутренние силы, приходящиеся на единицу площади поперечного сечения тела, называют напряжениями. Введение понятия напряжений позволяет проводить расчеты на прочность конструкций и их элементов.
В простейшем случае осевого растяжения цилиндрического стержня напряжение σ опеределяют как отношение растягивающее силы Р к начальной площади поперечного сечения Fo, т.е.
σ = P/Fo
Действие внешних сил приводит к деформации тела, т.е. к изменению его размером и формы. Деформация, исчезающая после разгрузки, называется упругой, а остающаяся в теле – пластической (остаточной).
Работоспособность отдельной группы деталей машин зависит не только от механических свойств, но и от сопротивления воздействию химически активной рабочей среды, если такое воздействие становится значительным, то определяющим становятся физико-химические свойства материала – жаростойкость и коррозионная стойкость.
Жаростойкость характеризует способность материала противостоять химической коррозии в атмосфере сухих газов при высокой температуре. У металлов нагрев сопровождается образованием на поверхности оксидного слоя (окалины).
Коррозионная стойкость – это способность металла противостоять электрохимический коррозии, которая развивается при наличие жидкой среды на поверхности металла и ее электрохимической неоднородности.
Для некоторых деталей машин, важные значение имеют физические свойства, характеризующие поведение материалов в магнитных, электрических и тепловых полях, а также под воздействием потоков высокой энергии или радиации. Их принято подразделять на магнитные, электрические, теплофизические и радиационные.
Способность материала подвергаться различным методам горячей и холодной обработки определяют по технологическим свойствам. К ним относят литейные свойства, деформируемость, свариваемость и обрабатываемость режущим инструментом. Технологические свойства позволяют производить формоизменяющую обработку и получать заготовки и детали машин.
К последней группе основных свойств относится стоимость материала, которая оценивает экономичность его использования. Ее количественным показателем является – оптовая цена – стоимость единицы массы материалы в виде слитков, профилей, порошка, штучных и сварных заготовок, по которым завод-изготовитель реализует свою продукцию машиностроительным и приборостроительным предприятиям.
Механические свойства, определяемые при статических нагрузках
Механические свойства характеризуют сопротивление материала деформации, разрушению или особенность его поведения в процессе разрушения. Эта группа свойств включает показатели прочности, жесткости (упругости), пластичности, твердости и вязкости. Основную группу таких показателей составляют стандартные характеристики механических свойств, которые определяют в лабораторных условиях на образцах стандартных размеров. Полученные при таких испытаниях показатели механических свойств оценивают поведение материалов под внешней нагрузкой без учета конструкции детали и условий эксплуатации.
По способу приложения нагрузок различают статические испытания на растяжение, сжатие, изгиб, кручение, сдвиг или срез. Наиболее распространены испытания на растяжения (ГОСТ 1497-84), которые дают возможность определить несколько важных показателей механических свойств.
Испытание на растяжение. При растяжении стандартных образцов с площадью поперечного сечения Fo и рабочей (расчетной) длиной lo строят диаграмму растяжения в координатах: нагрузка – удлинение образца (рис.1). На диаграмме выделяют три участка: упругой деформации до нагрузки Рупр.; равномерной пластической деформации от Рупр. до Рmax и сосредоточенной пластической деформации от Рmax до Рк. Прямолинейной участок сохраняется до нагрузки, соответствующей пределу пропорциональности Рпц. Тангенс угла наклона прямолинейного участка характеризует модуль упругости первого рода Е.

Рис. 1. Диаграмма растяжения пластичного металла (а) и диаграммы
условных напряжений пластичного (б) и хрупкого (в) металлов.
Диаграмма истинных напряжений (штриховая линия) дана для сравнения.
Пластическая деформация выше Рупр. идет при возрастающей нагрузке, так как металл в процессе деформирования упрочняется. Упрочнение материала при деформации называется наклепом.
Наклеп металла увеличивается до момента разрыва образца, хотя растягивающая нагрузка при этом уменьшается от Рmax до Рк (рис.1, а). Это объясняется появлением в образце местного утонения-шейки, в котором в основном сосредотачивается пластическая деформация. Несмотря на уменьшение нагрузки, растягивающие напряжения в шейке повышается до тех пор, пока образец не разрушится.
При растяжении образец удлиняется, а его поперечное сечение непрерывно уменьшается. Истинное напряжение определяются делением действующей в определенный момент нагрузки на площадь, которую образец имеет в этот момент (рис.1,б). Эти напряжения в повседневной практике не определяют, а пользуются условиями напряжениями, считая, что поперечное сечение Fo образца остается неизменным.
Напряжения σупр., σт, σв – стандартные характеристики прочности. Каждая получается делением соответствующей нагрузки Рупр. Рт и Рmax на начальную площадь поперечного сечения Fо.
Пределом упругости σупр. называют напряжение, при котором пластическая деформация достигает значений 0,005; 0,02 и 0,05%. Соответствующие пределы упругости обозначают σ0,005, σ0,02, σ0,05.
Условный предел текучести – это напряжение, которому соответствует пластическая деформация равная 0,2%; его обозначают σ0,2. Физический предел текучести σт определяют по диаграмме растяжения, когда на ней имеется площадка текучести. Однако, при испытаниях на растяжение у большинства сплавов нет площадки текучести на диаграммах. Выбранная пластическая деформация 0,2% достаточно точно характеризует переход от упругих деформаций к пластическим.
Временное сопротивление характеризует максимальную несущую способность материала, его прочность, предшествующую разрушению:
σв = Рmax / Fo
Пластичность характеризуется относительным удлинением δ и относительным сужением ψ:
где lk-конечная длина образца; lо и Fo – начальная длина и площадь поперечного сечения образца; Fк – площадь поперечного сечения в месте разрыва.
Для малопластичных материалов испытания на растяжение (рис. 1,в) вызывают значительные затруднения. Такие материалы, как правило, подвергают испытаниям на изгиб.
Испытание на изгиб. При испытании на изгиб в образце возникают как растягивающие, так и сжимающие напряжения. На изгиб испытывают чугуны, инструментальные стали, стали после поверхностного упрочнения и керамику. Определяемыми характеристиками служат предел прочности и стрела прогиба.
Предел прочности при изгибе вычисляют по формуле:
σи = M / W,
где М – наибольший изгибающий момент; W – момент сопротивления сечения, для образа круглого сечения
W = πd3 / 32
(где d – диаметр образца), а для образцов прямоугольного сечения W = bh2/6 , где b, h – ширина и высота образца).
Испытания на твердость. Под твердостью понимается способность материала сопротивляться внедрению в его поверхность твердого тела – индентора. В качестве индентора используют закаленный стальной шарик или алмазный наконечник в виде конуса или пирамиды. При вдавливании поверхностные слои материала испытывают значительную пластическую деформацию. После снятия нагрузки на поверхности остается отпечаток. Особенность происходящей пластической деформации состоит в том, что вблизи наконечника возникает сложное напряженное состояние, близкое к всестороннему неравномерному сжатию. По этой причине пластическую деформацию испытывают не только пластические, но и хрупкие материалы.
Таким образом, твердость характеризует сопротивление материала пластической деформации. Такое же сопротивление оценивает и временное сопротивление , при определении которого возникает сосредоточенная деформация в области шейки. Поэтому для целого ряда материалов численные значения твердости и временного сопротивления пропорциональны. На практике широко применяют четыре метода измерения твердости: твердость по Бринеллю, твердость по Виккерсу, твердость по Роквеллу и микротвердость.
При определении твердости по Бринеллю (ГОСТ 9012-59) в поверхность образца вдавливают закаленный шарик диаметром 10; 5 или 2,5 мм при действии нагрузки от 5000Н до 30000Н. После снятия нагрузки на поверхности образуется отпечаток в виде сферической лунки диаметром d.
При измерении твердости по Бринеллю используют заранее составленные таблицы, указывающие число твердости НВ В зависимости от диаметра отпечатка и выбранной нагрузки, чем меньше диаметр отпечатка, тем выше твердость.
Способ измерения по Бринеллю используют для сталей с твердостью <450 НВ, цветных металлов с твердостью <200 НВ. Для них установлена корреляционная связь между временным сопротивлением ( в МПа) и числом твердости НВ:
σв» 3,4 НВ – для горячекатаных углеродистых сталей;
σв» 4,5 НВ – для медных сплавов;
σв» 3,5 НВ – для алюминиевых сплавов.
При стандартном методе измерения по Виккерсу (ГОСТ 2999-75) в поверхность образца вдавливают четырехгранную алмазную пирамиду с углом при вершине 139°. Отпечаток получается в виде квадрата, диагональ которого измеряют после снятия нагрузки. Число твердости НV определяют с помощью специальных таблиц по значению диагонали отпечатка при выбранной нагрузке.
Метод Виккерса применяют главным образом для материалов, имеющих высокую твердость, а также для испытания на твердость деталей малых сечений или тонких поверхностных слоев. Как правило, используют небольшие нагрузки: 10,30,50,100,200,500 Н. Чем тоньше сечение детали или исследуемый слой, тем меньше выбирают нагрузку.
Число твердости по Виккерсу и по Бринеллю для материалов, имеющих твердость до 450 НВ, практически совпадают.
Измерение твердости по Роквеллу (ГОСТ 9013-59) наиболее универсален и наименее трудоемок. Число твердости зависит от глубины вдавливания наконечника, в качестве которого используют алмазный конус с углом при вершине 1200 или стальной шарик диаметром 1,588 мм. Для различных комбинаций нагрузок и наконечников прибор Роквелла имеет три измерительных шкалы: А.В.С. Твердость по Роквеллу обозначают цифрами, определяющими уровень твердости, и буквами HR с указанием шкалы твердости, например: 70HRA, 58HRC, 50HRB. Числа твердости по Роквеллу не имеют точных соотношений с числами твердости по Бринеллю и Виккерсу.
Шкала А (наконечник – алмазный конус, общая нагрузка 600Н). Эту шкалу применяют для особо твердых материалов, для тонких листовых материалов или тонких (0,6-1,0 мм) слоев. Пределы измерения твердости по этой шкале 70-85.
Шкала В (наконечник – стальной шарик, общая нагрузка 1000Н). При этой шкале определяют твердость сравнительно мягких материалов (<400НВ). Пределы измерения твердости 25-100.
Шкала С (наконечник – алмазный конус, общая нагрузка 1500Н). Эту шкалу используют для твердых материалов (>450НВ), например закаленных сталей. Пределы измерения твердости по этой шкале 20-67.
Определение микротвердости (ГОСТ 9450-76) осуществляют вдавливанием в поверхность образца алмазной пирамиды при небольших нагрузках (0,05-5Н) с последующим измерением диагонали отпечатка. Этим методом оценивают твердость отдельных зерен, структурных составляющих, тонких слоев или тонких деталей.
Механические свойства, определяемые при динамических нагрузках
При работе деталей машин возможны динамические нагрузки, при которых многие металлы проявляют склонность к хрупкому разрушению. Опасность разрушения усиливают надрезы – концентраторы напряжения. Для оценки склонности металла к хрупкому разрушению под влиянием этих факторов проводят динамические испытания на ударный изгиб на маятниковых копрах (рис. 2). Стандартный образец устанавливают на две споры и посредине наносят удар, приводящий к разрушению образца. По шкале маятникова копра определяют работу К, затраченную на разрушение, и рассчитывают основную характеристику, получаемую в результате этих испытаний – ударную вязкость:
КС = К / S01 , [МДж/м2],
где S01 , площадь поперечного сечения образца в месте надреза.

Рис. 2. Схема маятникова копра (а) и испытание на удар (б):
1 – образец; 2 – маятник; 3 – шкала; 4 – стрелка шкалы; 5- тормоз.
В соответствии с ГОСТ 9454-78 предусмотрены испытания образцов трех видов: U-образным (радиус надреза r=1 мм); V-образным (r=0,25 мм) и Т-образным (трещина усталости, созданная в основании надреза. Соответственно ударную вязкость обозначает: КСU, KCV, KCT. Ударная вязкость из всех характеристик механических свойств наиболее чувствительна к снижению температуры. Поэтому испытания на ударную вязкость при пониженных температурах используют для определения порога хладноломкости – температуры или интервала температур, в котором происходит снижение ударной вязкости. Хладноломкость – способность металлического материала терять вязкость, хрупко разрушаться при понижении температуры. Хладноломкость проявляется у железа, стали, металлов и сплавов, имеющих объемно-центрированную кубическую (ОЦК) или гексагональную плотноупакованную (ГП) решетку. Она отсутствует у металлов с гранецентрированной кубической (ГЦК) решеткой.
Механические свойства, определяемые при переменных циклических нагрузках
Многие детали машин (валы, шатуны, зубчатые колеса) испытывают во время работы повторяющиеся циклические нагружения. Процессы постепенного накопления повреждений в материале под действием циклических нагрузок, приводящие к изменению его свойств, образованию трещин, их развитию и разрушению, называют усталостью, а свойство противостоять усталости – выносливостью (ГОСТ 23207-78). О способности материалы работать в условиях циклического нагружения судят по результатам испытаний образцов на усталость (ГОСТ 25.502-79). Их проводят на специальных машинах, создающих в образцах многократное нагружение (растяжение – сжатие, изгиб, кручение). Образцы испытывают последовательно на разных уровнях напряжений, определяя число циклов до разрушения. Результаты испытаний изображают в виде кривой усталости, которая строится в координатах: максимальное напряжение цикла σmax / или σв ) – число циклов. Кривые усталости позволяют определять следующие критерии выносливости:
– цик?
