Какие свойства функции синус
Свойства функции y=sin(x) и ее график.
График функции 
(синусоида)
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
![file.[2]](https://ya-znau.ru/information/userfiles/73/file.%5B2%5D.jpg)
- Точки пересечения с осями координат:
![file.[3]](https://ya-znau.ru/information/userfiles/73/file.%5B3%5D.jpg)
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
![file.[4]](https://ya-znau.ru/information/userfiles/73/file.%5B4%5D.jpg)
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).
Рис.1.
Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции область значений: 
. Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.
Синус — периодическая функция с наименьшим положительным периодом 
: 
, таким образом, через промежутки длиной вид графика функции повторяется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние 
, где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси 
значение 
. Тогда соответствующее значение 
, то есть график функции проходит через начало координат.
На оси 
значение 
. Поэтому необходимо найти такие значения 
, при которых , то есть ордината соответствующей точки единичной окружности, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при 
(см. рис. 1).
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, 
при всех 
, а также, учитывая период, при всех 
.
Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому 
при 
.
Промежутки возрастания и убывания. Учитывая периодичность функции с периодом 
, достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке 
.
Если 
(рис. 3, а), то при увеличении аргумента 
ордината соответствующей точки единичной окружности увеличивается (то есть 
, следовательно, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков 
Рис.2 Рис.3
Если 
(рис.3,б), то при увеличении аргумента 
ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков 
Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , например на промежутке 
. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке 
. Учитывая нечетность функции (ее график симметричен относительно начала координат), для построения графика на промежутке 
отображаем полученную кривую симметрично относительно начала координат (рис. 5).
Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на 
, где k — целое число). Получаем график, который называется синусоидой .(Рис.6)
Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой 
. Такие процессы называют гармоническими колебаниями.
График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным переносом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой 
, где А — амплитуда
колебания, 
— частота, 
— начальная фаза, 
— период колебания.
СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число).
- Область значений:
Функция четная:
(график симметричен относительно оси
).- Функция периодическая с периодом :
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
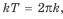
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:.
Рис.7
Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .
Как видим, наибольшее значение функции равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .
Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при .
Косинус — четная функция: , поэтому ее график симметричен относительно оси .
Косинус — периодическая функция с наименьшим положительным периодом : . Таким образом, через промежутки длиной вид графика функции повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .
Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 0 при , а также, учитывая период, при всех .
Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому при
Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 9, а), то при увеличении аргумента абсцисса соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .
Если (рис. 9, б), то при увеличении аргумента абсцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Рис.8 Рис.9
Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу
Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также
абсциссы и ординаты этих точек. Так как , то при повороте
прямоугольника около точки 
на угол — против часовой стрелки он перейдет в прямоугольник 
. Но тогда 
. Следовательно, 00.
Укажем также формулы, которые нам понадобятся далее:
.
Тогда,
Таким образом, 
.
Учитывая, что 
, график функции можно получить из графика функции его параллельным переносом вдоль оси на 
(рис. 11). Полученный график называется косинусоидой (рис. 12).
Рис.11
Рис.12
График функции 
(тангенсоида)
Свойства функции :
1. Область определения:
2. Область значений: 
3. Функция нечетная: 
4. Функция периодическая с периодом 
5. Точки пересечения с осями координат: 
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
График функции 
(котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная: 
4. Функция переодическая с периодом 
5. Точки пересечения с осями координат: 
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Источник
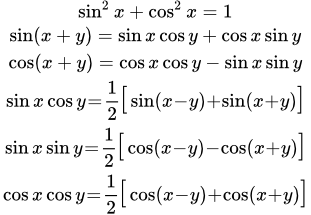
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Содержание
Геометрическое определение синуса и косинусаПринятые обозначенияГрафики функций синус, y = sin x, и косинус, y = cos xСвойства синуса и косинусаПериодичностьЧетностьОбласть определения и значений, экстремумы, возрастание, убываниеОсновные формулыСумма квадратов синуса и косинусаФормулы синуса и косинуса от суммы и разностиФормулы произведения синусов и косинусовФормулы суммы и разностиВыражение синуса через косинусВыражение косинуса через синусВыражение через тангенсТаблица синусов и косинусов, тангенсов и котангенсовВыражения через комплексные переменныеФормула ЭйлераВыражения через гиперболические функцииПроизводныеИнтегралыРазложения в рядыСеканс, косекансОбратные функцииАрксинус, arcsinАрккосинус, arccosСм. также: Тангенс, котангенс, свойства, графики, формулы
Обратные тригонометрические функции, их графики и формулы
Геометрическое определение синуса и косинуса
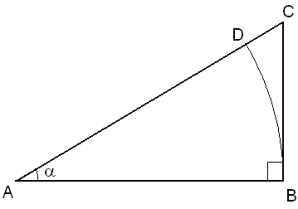Прямоугольный треугольник.
|BD| – длина дуги окружности с центром в точке A.
α – угол, выраженный в радианах.
Синус (sin α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
Графики функций синус, y = sin x, и косинус, y = cos x
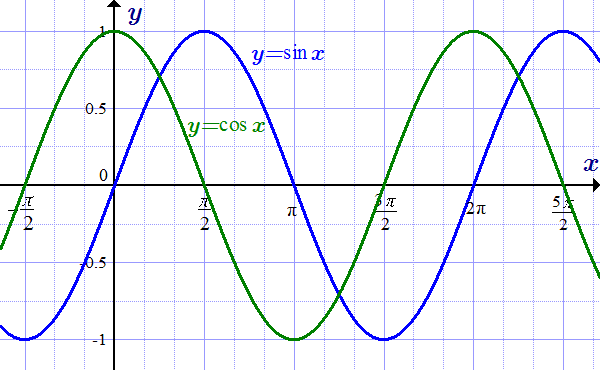Графики функций y=sin(x) и y=cos(x).
Графики синуса и косинуса смещены по оси x друг относительно друга на :
.
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
Четность
Функция синус – нечетная. Функция косинус – четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n – целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | –1 ≤ y ≤ 1 | –1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = –1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
Далее мы полагаем, что – целое число.
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При , имеем:
; .
При :
; .
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.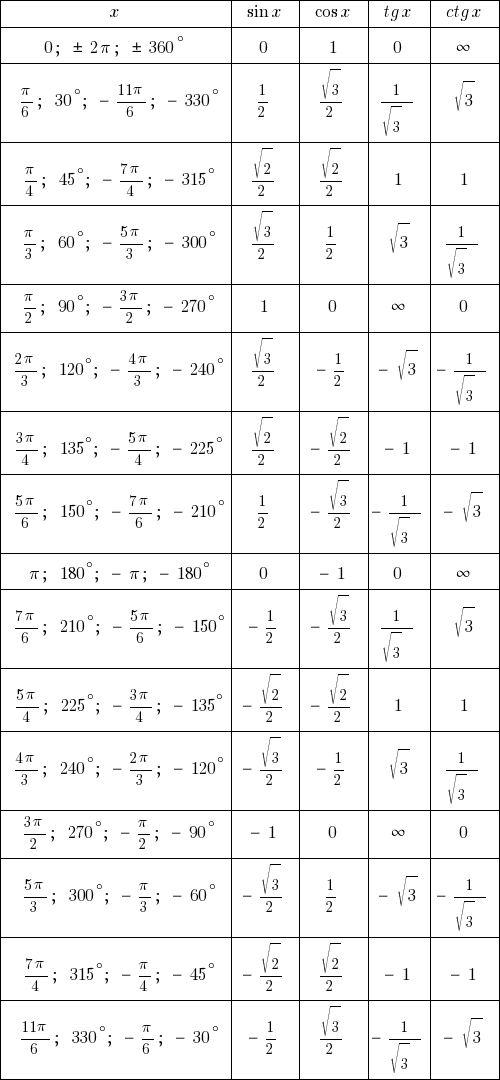 
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
; .
Интегралы
;
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
{ –∞ < x < +∞ }
{ –∞ < x < +∞ }
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: 15-02-2014 Изменено: 10-05-2020
См. также: Тангенс, котангенс, свойства, графики, формулы
Обратные тригонометрические функции, их графики и формулы
Источник
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство – знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство – периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: “угол первой, второй, третьей или четвертой координатной четверти”. Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
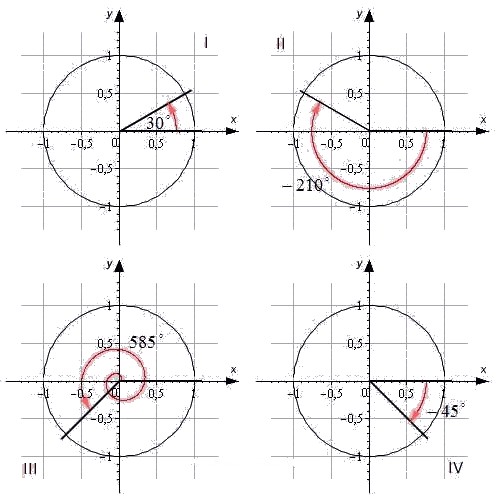
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° – угол третьей четверти. Угол -45° – это угол четвертой четверти.
При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
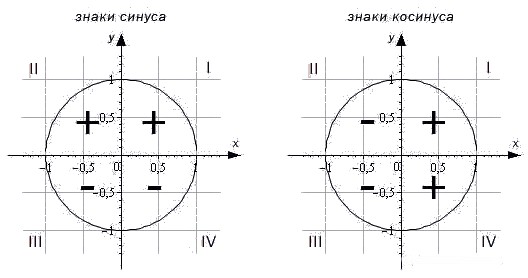
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус – это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной – отрицательна.
Косинус – это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс – отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки – отрицательным. Аналогично определяются знаки котангенса по четвертям.
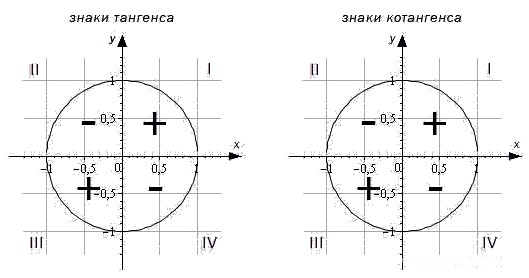
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус – в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус – в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус – в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус – в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности – одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin13π5=sin3π5+2π=sin3π5
tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
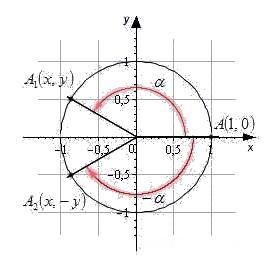
Точка A1(x, y) – результат поворота начальной точки A0(1, 0) вокруг центра окружности на угол α. Точка A2(x, -y) – результат поворота начальной точки на угол -α.
Точки A1и A2 симметричны относительно оси абсцисс. В случае, когда α=0°, ±180°, ±360° точки A1и A2 совпадают. Пусть одна точка имеет координаты (x, y), а вторая – (x, -y). Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α=y, cos α=x, tg α=yx, ctg α=xysin-α=-y, cos-α=x, tg-α=-yx, ctg-α=x-y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin-α=-sin αcos-α=cos αtg-α=-tg αctg-α=-ctg α
Согласно этому свойству, справедливы равенства
sin-48°=-sin 48°, ctgπ9=-ctg-π9, cos 18°=cos-18°
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Источник