Какие свойства дробей вы знаете

В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
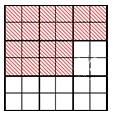
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
Источник
Основное свойство дроби
Если ad=bc, то две дроби frac{a}{b}и frac{c}{d} считаются равными. К примеру, равными будут дроби frac35и frac{9}{15}, так как 3 cdot 15 = 15 cdot 9, frac{12}{7}и frac{24}{14}, так как 12 cdot 14 = 7 cdot 24.
Из определения равенства дробей следует, что равными будут дроби frac{a}{b}и frac{am}{bm}, так как a(bm)=b(am) — наглядный пример применения сочетательного и переместительного свойств умножения натуральных чисел в действии.
Значит frac{a}{b} = frac{am}{bm} — так выглядит основное свойство дроби.
Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.
Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.
Сокращать дроби принято, опираясь на основное свойство дроби.
Например, frac{45}{60}=frac{15}{20}(числитель и знаменатель делится на число 3); полученную дробь снова можно сократить, разделив на 5, то есть frac{15}{20}=frac 34.
Несократимая дробь — это дробь вида frac 34, где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.
Приведение дробей к общему знаменателю
Возьмем в качестве примера две дроби: frac{2}{3}и frac{5}{8} с разными знаменателями 3 и 8. Для того, чтобы привести данные дроби к общему знаменателю и сначала перемножим числитель и знаменатель дроби frac{2}{3}на 8. Получаем следующий результат: frac{2 cdot 8}{3 cdot 8} = frac{16}{24}. Затем умножаем числитель и знаменатель дроби frac{5}{8}на 3. Получаем в итоге: frac{5 cdot 3}{8 cdot 3} = frac{15}{24}. Итак, исходные дроби приведены к общему знаменателю 24.
Арифметические действия над обыкновенными дробями
Сложение обыкновенных дробей
а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:
frac{a}{b}+frac{c}{b}=frac{a+c}{b};
б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а):
frac{7}{3}+frac{1}{4}=frac{7 cdot 4}{3}+frac{1 cdot 3}{4}=frac{28}{12}+frac{3}{12}=frac{31}{12}.
Вычитание обыкновенных дробей
а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:
frac{a}{b}-frac{c}{b}=frac{a-c}{b};
б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а).
Умножение обыкновенных дробей
Умножение дробей подчиняется следующему правилу:
frac{a}{b} cdot frac{c}{d}=frac{a cdot c}{b cdot d},
то есть перемножают отдельно числители и знаменатели.
Например:
frac{3}{5} cdot frac{4}{8} = frac{3 cdot 4}{5 cdot 8}=frac{12}{40}.
Деление обыкновенных дробей
Деление дробей производят следующим способом:
frac{a}{b} : frac{c}{d}= frac{ad}{bc},
то есть дробь frac{a}{b} умножается на дробь frac{d}{c}.
Пример: frac{7}{2} : frac{1}{8}=frac{7}{2} cdot frac{8}{1}=frac{7 cdot 8}{2 cdot 1}=frac{56}{2}.
Взаимно обратные числа
Если ab=1, то число b является обратным числом для числа a.
Пример: для числа 9 обратным является frac{1}{9}, так как 9 cdot frac{1}{9}=1, для числа 5 — frac{1}{5}, так как 5 cdot frac{1}{5}=1.
Десятичные дроби
Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10,000, …, 10^n.
Например: frac{6}{10}=0,6;enspace frac{44}{1000}=0,044.
Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.
Например: 5frac{1}{10}=5,1;enspace frac{763}{100}=7frac{63}{100}=7,63.
В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10.
Пример: 5 — делитель числа 100, поэтому дробь frac{1}{5}=frac{1 cdot 20}{5 cdot 20}=frac{20}{100}=0,2.
Арифметические действия над десятичными дробями
Сложение десятичных дробей
Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.

Вычитание десятичных дробей
Выполняется аналогично сложению.

Умножение десятичных дробей
При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.
Давайте выполним умножение 2,7 на 1,3. Имеем 27 cdot 13=351. Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=2). В итоге получаем 2,7 cdot 1,3=3,51.
Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:

Для умножения на 10, 100, 1000, надо в десятичной дроби перенести запятую на 1, 2, 3 цифры вправо (в случае необходимости справа приписывается определенное число нулей).
Например: 1,47 cdot 10,000 = 14 700.
Деление десятичных дробей
Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.

Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:
.png)
Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Первым делом, умножим делимое и делитель дроби на 100, то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112, то есть задача сводится к уже рассмотренному случаю:
.png)
Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.
2,8 : 0,09= frac{28}{10} : frac {9}{100}= frac{28 cdot 100}{10 cdot 9}=frac{280}{9}=31 frac{1}{9}.
Источник
$blacktriangleright$ Пример 1. $4$ друга в кафе заказали пиццу. Официант принес пиццу, разрезанную на $8$ частей. Сколько кусков пиццы досталось каждому другу, если они разделили пиццу поровну? Какая часть пиццы досталась каждому?
Решение:
Так как всего кусков $8$, а друзей четверо, то каждому досталось $8:4 = 2$ куска пиццы.
Нарисуем схему к этой задаче и обозначим разным цветом части пиццы, которые достались каждому другу. Мы видим, что каждому другу досталось по $2$ куска $dfrac{1}{8}$ части пиццы, то есть по $dfrac{2}{8}$ частей пиццы.
С другой стороны, если $1$ пиццу разделить поровну на $4$ части, то каждому достанется $dfrac{1}{4}$ часть пиццы.
Следовательно, $dfrac{2}{8} = dfrac{1}{4}$.
Заметим, что дробь $dfrac{1}{4}$ можно получить из дроби $dfrac{2}{8}$, если числитель и знаменатель разделить на $2$.
Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же, отличное от нуля число, то получится равная ей дробь.
Когда числитель и знаменатель дроби делят на одно и то же натуральное число, говорят, что дробь сокращают. Если числитель и знаменатель дроби нельзя разделить на одно и то же натуральное число, такую дробь называют несократимой.
Например, дробь $dfrac{15}{20}$ можно сократить, так как числитель и знаменатель делятся на одно и то же число. $dfrac{15}{20} = dfrac{15:5}{20:5} = dfrac{3}{4}$ или записывают $dfrac{15}{20}$ в виде $dfrac{5cdot 3}{5cdot 4}$ и сокращают одинаковые множители $dfrac{15}{20} = dfrac{3}{4}$.
Дробь $dfrac{13}{25}$ нельзя сократить, так как нет такого натурального числа, на которое делились бы и числитель, и знаменатель, значит, эта дробь несократимая.
Для каждой дроби существует единственная, равная ей, несократимая дробь.
Например, $dfrac{12}{36} = dfrac{6cdot 2}{18cdot 2} = dfrac{6}{18} = dfrac{3cdot 2}{9cdot 2} = dfrac{3}{9} = dfrac{1cdot 3}{3cdot 3} = dfrac{1}{3}$ — несократимая.
Если числитель дроби делится на знаменатель, то дробь равна частному от деления числителя на знаменатель.
Например, $dfrac{25}{5} = dfrac{5cdot 5}{1cdot 5} = dfrac{5}{1} = 5$.
Правильной дробью называется дробь, у которой числитель меньше знаменателя:
$dfrac{10}{23}$ — правильная дробь, так как $10 < 23$.
Правильная дробь всегда меньше 1.
Неправильной дробью называется дробь, у которой числитель больше знаменателя:
$dfrac{23}{10}$ — неправильная, так как $23 > 10$.
Неправильная дробь больше или равна 1.
Из неправильной дроби можно выделить целую часть, для этого нужно разделить числитель на знаменатель. Неполное частное будет целой частью, остаток — числителем, а делитель останется знаменателем:
$23:10 = 2 (ост.3)$, следовательно, $dfrac{23}{10}$ = $2$ $dfrac{3}{10}$
Число, состоящее из целой и дробной частей, называют смешанным. $2$ $dfrac{3}{10}$ — смешанное число.
Чтобы найти числитель неправильной дроби, нужно целую часть умножить на знаменатель и прибавить числитель смешанного числа.
Задачки от мистера Фокса
№1. Сократите дроби, если это возможно:
$1)$ $dfrac{2}{4}$;
$2)$ $dfrac{3}{6}$;
$3)$ $dfrac{5}{20}$;
$4)$ $dfrac{49}{56}$;
$5)$ $dfrac{7}{15}$;
$6)$ $dfrac{22}{55}$.
$1)$ $dfrac{2}{4} = dfrac{1cdot 2}{2cdot 2} = dfrac{1}{2}$;
$2)$ $dfrac{3}{6} = dfrac{1cdot 3}{2cdot 3} = dfrac{1}{2}$;
$3)$ $dfrac{5}{20} = dfrac{1cdot 5}{4cdot 5} = dfrac{1}{4}$;
$4)$ $dfrac{49}{56} = dfrac{7cdot 7}{8cdot 7} = dfrac{7}{8}$;
$5)$ $dfrac{7}{15}$ — несократимая;
$6)$ $dfrac{22}{55} = dfrac{2cdot 11}{5cdot 11} = dfrac{2}{5}$.
№2. Решите уравнение $dfrac{5}{8} = dfrac{x}{48}$, используя основное свойство дроби.
$dfrac{5}{8} = dfrac{x}{8cdot 6}$
По основному свойству дроби, дроби будут равными, если знаменатель и числитель умножить на одно и то же число, значит:
$x = 5cdot 6$
$x = 30$
.
Проверим:
$dfrac{30}{48} = dfrac{5cdot 6}{8cdot 6} = dfrac{5}{8}$
.
Ответ: $x = 30$.
№3. Представьте смешанное число в виде неправильной дроби:
$1)$ $4 dfrac{4}{25}$;
$2)$ $3 dfrac{3}{15}$;
$3)$ $2 dfrac{11}{12}$.
$1)$ $4cdot 25 + 4 = 104$, значит $4$ $dfrac{4}{25} = dfrac{104}{25}$;
$2)$ $3cdot 15 + 3 = 48$, значит $3$ $dfrac{3}{15} = dfrac{48}{15}$;
$3)$ $2cdot 12 + 11 = 35$, значит $2$ $dfrac{11}{12} = dfrac{35}{12}$.
№4. Выделите целую часть:
$1)$ $dfrac{124}{5}$;
$2)$ $dfrac{45}{12}$;
$3)$ $dfrac{1000}{37}$.
$1)$ $124:5 = 24 (ост. 4)$, значит $dfrac{124}{5} = 24 dfrac{4}{5}$;
$2)$ $45:12 = 3 (ост. 9)$, значит $dfrac{45}{12} = 3 dfrac{9}{12}$;
$3)$ $1000:37 = 27 (ост.1)$, значит $dfrac{1000}{37} = 27 dfrac{1}{37}$.
№5. При каких натуральных значениях $a$ дробь $dfrac{3cdot a + 4}{12}$ будет правильной?
Так как у правильной дроби числитель меньше знаменателя, то нам нужно найти такие значения a, при которых верно неравенство $3cdot a + 4 < 12$.
$3cdot a + 4 < 12$
Чтобы неравенство $3cdot a + 4 < 12$ выполнялось, нужно, чтобы $3cdot a$ было меньше $8$.
$3cdot a < 8$
$a < dfrac83$
.
Выделим целую часть:
$dfrac{8}{3} = 2 dfrac{2}{3}$
.
Значит, при $a = 1$ или $a = 2$ дробь $dfrac{3cdot a + 4}{12}$ будет правильной.
Проверим: $a = 1$, тогда $dfrac{3cdot 1 + 4}{12}$ = $dfrac{7}{12}$ — правильная.
Если $a = 2$, тогда $dfrac{3cdot2+4}{12} = dfrac{10}{12}$ — правильная.
Также дробь $dfrac{3cdot a + 4}{12}$ будет правильной при $a = 0$, но поскольку в задаче спрашивается только про натуральные значения $a$, а ноль не является натуральным числом, то мы его не рассматриваем.
Ответ: при $a = 1$ или $a = 2$ дробь $dfrac{3cdot a + 4}{12}$ будет правильной.
Источник
Ключевые слова конспекта: дроби, обыкновенная дробь, правильные и неправильные дроби, основное свойство дроби, сравнение дробей, арифметические действия с дробями, нахождение части от целого и целого по его части.
Одна или несколько равных частей единицы называются обыкновенной дробью. Дробь 3/4 означает, что единицу разделили на 4 части и взяли 3 таких части.

Дробь можно рассматривать и как результат деления натуральных чисел. Частное от деления натуральных чисел а и b можно записать в виде дроби a/b — где делимое а — числитель, а делитель b — знаменатель.

Правильная и неправильная дробь
Дробь, в которой числитель меньше знаменателя, называется правильной, а дробь, где числитель больше или равен знаменателю, — неправильной.

Число, состоящее из целой и дробной частей, можно обратить в неправильную дробь. Для этого нужно умножить целую часть на знаменатель и к произведению прибавить числитель данной дроби. Полученная сумма будет числителем дроби, а знаменателем остается знаменатель дробной части.

Из любой неправильной дроби можно выделить целую часть. Для этого нужно разделить с остатком числитель на знаменатель. Частное от деления — это целая часть, остаток — это числитель, делитель — это знаменатель.

Основное свойство дроби
Определение. Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной.

Основное свойство дроби используют при сокращении дробей. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дробей.

Сравнение дробей
- Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
- Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к наименьшему общему знаменателю;
- сравнить полученные дроби.

Чтобы привести дроби к наименьшему общему знаменателю, нужно:
- найти наименьшее общее кратное (НОК) знаменателей дробей (оно и будет их общим знаменателем);
- разделить общий знаменатель на знаменатель данных дробей, т. е. найти для каждой дроби дополнительный множитель;
- умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Арифметические действия с обыкновенными дробями
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.
При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

Умножение дробей
- Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

- При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

Деление дробей
Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Нахождение части от целого (дроби от числа)
Чтобы найти часть от целого, нужно число, соответствующее целому, разделить на знаменатель дроби, выражающей эту часть, и результат умножить на числитель той же дроби.
Задача нахождения части от целого по существу является задачей нахождения дроби от числа. Чтобы найти дробь (часть) от числа, необходимо число умножить на эту дробь.

Нахождение целого по его части (числа по его дроби)
Чтобы найти целое по его части, нужно число, соответствующее этой части, разделить на числитель дроби, выражающей эту часть, и результат умножить на знаменатель той же дроби.
Задача нахождения целого по его части по существу является задачей нахождения числа по его дроби. Чтобы найти число по его дроби, необходимо данное значение разделить на эту дробь.

Это конспект по теме «Обыкновенная дробь». Выберите дальнейшие действия:
- Перейти к следующему конспекту: Десятичная дробь
- Вернуться к списку конспектов по Математике.
- Проверить знания по Математике.
Источник
Тут недавно, в комментариях к интересной математике, меня попросили объяснить, что такое пропорция и отношение. Я так полагаю, что ни один математик сегодня не в состоянии толком объяснить пропорции. Почему? Во-первых, их этому не учили. Во-вторых, у них нет собственных мозгов, думают математики только определениями. Но начать нам нужно с темы “дроби и свойства дробей”. Есть там один очень примечательный фрагмент, который нам и покажет, где рождаются пропорции.
Возьмем математический справочник и почитаем. Почему справочник? Там нет мусора, который так любят совать в учебники их авторы. Всё коротко, не совсем ясно, но пригодно для широкого употребления. Справочник рассчитан на учащихся средних специальных заведений. То есть, на тех, кто школу уже закончил и всё давно забыл, а учебники выбросил. А тут под рукой справочник – всё самое основное для быстрого восстановления памяти.
| Дроби и свойства дробей |
Начинается этот раздел из грозного определения рациональных чисел. Они же дроби. Лично я ничего не имею против дробей, но я против несокрушимой тупости определений. Буквы в определение можно вписать любые и смысл его от этого не изменится.
| Варианты обозначения дробей |
Я так же против деления чисел на натуральные, целые, рациональные и так далее. Этот числовой расизм – бытовой пережиток каменного века. Разделяй и властвуй – вот какой принцип заложен в основу деления чисел по внешнему виду. О чем это я? А вот о чём.
Вы внимательно прочитали текст на первой картинке? А теперь попробуйте ответить на вопрос “Что такое единица?”. Что бы вы не сказали, я всегда могу возразить, что ваш ответ не правильный. Фокус в том, что однозначно правильного ответа не существует. Есть множество правильных ответов, из которых я всегда могу выбрать не тот, что сказали вы. Что бы поставить вам двойку. Или назвать ваш ответ правильным, что бы поставить отлично.
Смотрите. Любая дробь, у которой числитель равен знаменателю, всегда равна единице и называется это неправильной дробью. Так что такое единица? Это и натуральное число, и целое число, и рациональное число, и неправильная дробь… Теперь попробуйте угадать с трех раз, какой ответ хочет от вас услышать учитель? А ведь у учителя в запасе есть и четвертый вариант.
Но дробь ещё можно называть отношением. Хотя, по другим источникам, отношением двух чисел называется частное этих чисел. То есть не само обозначение деления, а его результат. Но в таком случае и простая дробь, она же обыкновенная дробь – это не что иное, как недоделанное деление. Так сказать, “протокол о намерениях”. Ведь в числите и знаменателе могут стоять натуральные числа (иррациональное число), одинокие буквы (простая дробь), математические выражения (алгебраическая дробь).
Вам ещё не страшно? Добавим к этому гаданию на кофейной гуще ещё один рецепт. Из древнего Вавилона. Дело в том, что у древних вавилонян не было понятия дробного числа. Дробь они изображали как умножение числа (натуральное число больше единицы) на обратное число (единица, деленная на число). Вот как это выглядит в классическом обозначении дроби.
| Вавилонский вариант дроби |
Наши математики такое развитие сюжета тупо игнорируют. Ведь здесь мы лицом к лицу сталкиваемся с вопросом: “А что такое умножение и деление?”. Судя по всему, современные математики не способны внятно ответить на этот вопрос.
Лично я древним математикам верю гораздо больше, чем современным. Ведь математика в современном супермаркете отличается от математики на базаре древнего Вавилона только тем, что на современных ценниках присутствуют нули, которых пять тысяч лет назад не было. Числа, сложение, вычитание, умножение, деление, измерение длины, времени, углов, вычисление площади, объема, квадратного корня… Всё, чем мы ежедневно пользуемся сегодня в быту, и даже больше, появилось ещё в те незапамятные времена.
Современные математики подарили нам ноль и никому не понятные толстые учебники. А ещё они здорово (или не очень) умеют решать те задачи, которые их заставляют решать. Но все эти решения больше похожи на пляски шаманов с бубнами, чем на осмысленные действия.
Но это всё так, старческое брюзжание. Для общего развития. Что делать вам? Тупо учите то, что вас заставляют учить, и отвечайте то, что от вас хотят услышать. Свое мнение оставляйте при себе. Может быть, когда-нибудь, вы сможете его высказать без вреда для себя. А пока… Если вы понимаете больше, чем окружающие, это уже ваш плюс в борьбе за место под солнцем.
Теперь вернемся к математике и рассмотрим сравнение дробей.
Источник
