Какие свойства делимости чисел

Признак делимости на 2
Чётное число – это число, которое делится на 2.
Нечётное число – не делится на 2.
Число делится на два, в том случае если его последняя цифра является чётной или нуль. Во всех остальных случаях – не делится.

Число 52 738 делится на 2, так как у него последняя цифра 8 которая является чётной.
Число 7691 не делится на 2, так как цифра 1 находящаяся в конце нечетная.
Число 1250 делится на 2, так как цифра, которая находится в конце нуль.
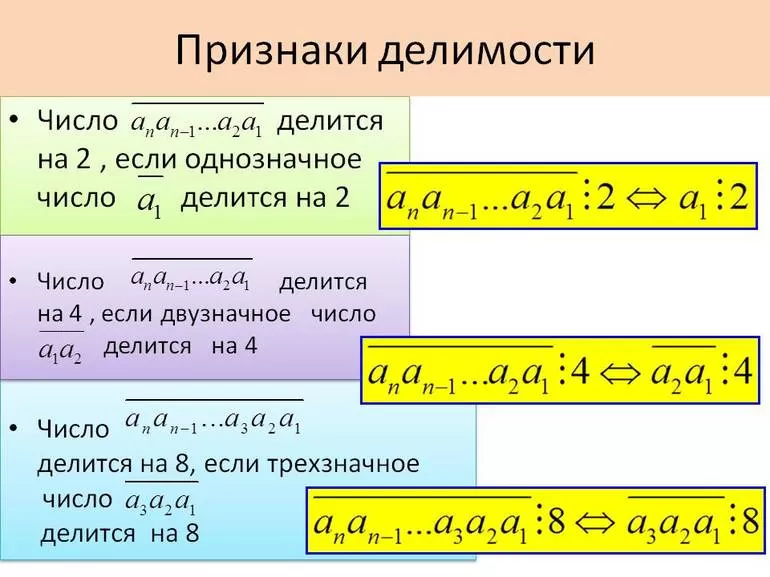
Признак делимости на 4
Число делится на 4, при условии, если две последние его цифры нули либо образуют число, которое делится на 4. В остальных случаях – не делится.
Число 31 800 делится на 4, так как в его окончании находятся два нуля.
Число 325 734 не делится на 4, так как крайние две цифры дают число 34, которое не делится на 4.
Число 15 608 делится на 4, так как две конечные цифры 0 и 8 дают число 8, которое делится на 4.
Признак делимости на 8
Число делится на 8, в случае, когда три последние цифры его нули или формируют число, делящееся на 8. В остальных случаях – не делится.
Число 225 000 делится на 8, так как оканчивается тремя нулями.
Число 180 004 не делится на 8, так как три крайние цифры дают число 4, которое не делится на 8.
Число 112 120 делится на 8 так как три цифры находящиеся в конце дают число 120, которое делится на 8.
Можно указать аналогичные признаки и делимости на 16, 32, 64 и т. п., но это не будет иметь практического значения.
Признаки делимости на 3 и на 9
На число 3 делятся числа, сумма составляющих цифр которых делится на 3.
На число 9 делятся числа, сумма составляющих цифр которых делится на 9.
Число 17 835 делится на 3 и не может быть разделено на 9, так как сумма его цифровых значений 1 + 7 + 8 + 3 + 5 = 24 может быть разделено на 3 и не делится на 9.
Число 106 499 не может быть разделено ни на 3, ни на 9, так как составляющие его цифры в сумме даёт число 29 которое не делится как на 3, так и на 9.
Число 52 632 может быть разделено на 9, так как сумма цифр входящих его состав 18 которое делится на 9.
Признак делимости на 6
Число делится на 6, когда оно может быть разделено одновременно на 2 и на 3. В противном случае – не делится.
Число 126 может быть разделено на 6, в виду того, что оно делится и на 2 и на 3.
Признак делимости на 5
На 5 делятся те числа, у которых последняя цифра 0 или 5. Другие – не делятся.
Число 240 может быть разделено на 5, так как последняя цифра 0.
Число 554 не делится на 5, так как последняя цифра 4.
Признак делимости на 25
На 25 можно разделит только те числа, у которых две крайние цифры нули либо формируют число, которое может быть разделено на 25, например числа оканчивающиеся на 00, 25, 50 или 75. Другие – не делятся.
Число 7150 можно разделить на 25, так как оканчивается на 50.
Число 4855 не получится разделить на 25.
Признаки делимости на 10, 100 и 1000
Числа делятся на 10, когда последняя цифра является нулём.
Числа делятся на 100, если две последние цифры этих чисел нули.
Числа делятся на 1000, если три конечные цифры у них нули.
8200 можно разделить на 10 и на 100.
542 000 можно разделить на 10, 100 и 1000.
Признак делимости на 11
На 11 можно разделить только те числа, у которых сумма цифр, находящихся на нечётных местах, или равна сумме цифр, находящихся на чётных местах, либо отличны от нее на число, которое делится на 11.
103 785 можно разделить на 11, так как 1 + 3 + 8 = 12 и 0 + 7 + 5 = 12
9 163 627 можно разделить на 11, так как при вычитании из 28 числа 6 получается 22, которое делится на 11. ( 9 + 6 + 6 + 7 = 28 ) ( 1 + 3 + 2 = 6 )
461 025 не может разделено на 11, в виду того что числа 7 и 11 взаимно не ровны, а их разность 4 на 11 не разделить. ( 11 – 7 = 4 ),( 4 + 1 + 2 = 7 ), ( 6 + 0 + 5 = 11).
Существуют признаки делимости так же и на другие числа, но эти признаки гораздо сложнее.
Источник
Дроби с кратными от 1 до 5
На единицу делится любое целое число.
Самым простым правилом является делимость на число два: если натуральное число оканчивается на четную цифру, то оно кратно двум. Если в конце стоит нечетная цифра, какими являются 1, 3, 5, 7, 9, то число на два не делится. То есть чтобы поделить многозначное число на два, в конце числа должна стоять одна из таких цифр: 2, 4, 6, 8, 0.
Пример: 6942 является четным, поскольку в конце четная цифра, поэтому оно кратно двум; число 19678456 также кратно двум, так как в конце стоит четная цифра 6. А вот число 6796345 не делится на 2, поскольку оно нечетное. Также нельзя получить ответ без остатка с такой суммы, как 398573 по этой же причине.

Деление на три имеет свое правило: нужно сложить все цифры, а затем проверить, делится ли сумма на три. Если да, то и данность разделится на три. Если нет, значит, не делится.
Например, возьмем 3576. Складываем 3+5+7+6=21. Полученную сумму 21 делим на три, получается семь. Значит, оно кратно трем без остатка. Проведем разложение шестизначного номера 353388. Оно раскладывается на три, поскольку сумма равна тридцати (3+5+3+3+8+8=30). Еще возьмем, например, 5819. Складываем: 5+8+1+9=23, полученная сумма не делится на три без остатка. Также и 2947 невозможно разделить, поскольку остаются тройки.
Правило делимости на четыре звучит так: если две последние цифры номера кратны четырем либо оно в конце имеет два нуля, то отношение получится без остатка.
Например, 1000 делится на четыре, поскольку в конце 00. Делится также и 3824, так как в конце 24, которое кратно этому делителю. А вот 2986 не делится на четыре, так как 86 не кратно четырем, и 29087 тоже не может остаться целым, поскольку с 87 нельзя произвести расчета. Еще пример: четырехзначный номер 2648 можно разделить на этот делитель, так как 48:4=12.
Довольно простым правилом является делимость на пять. Частное получается без остатка, если в конце заданного числа стоит 5 или 0. Если оно не заканчивается одной из этих цифр, то при делении возникнет остаток.
Проверим правило, взяв пятизначное число 45765. Оно кратно пяти без остатка, так как заканчивается на пять. Также 45030 можно разделить, поскольку в конце ноль. А вот четырехзначное число 4321 без остатка не делится.
Свойства делителей от 6 до 10
Составное шесть состоит из произведения двух последовательных чисел — 2 и 3. Теория кратности такова: число 6 составное, поэтому необходимо, чтобы одновременно действовали два правила признака делимости. Нужно, чтобы число было кратно и двум, и трем сразу.
Например, проверке подвергаются трехзначные числа 756 и 168. Они четные, поэтому делятся на два. Теперь нужно сложить 7+5+6=18, становится ясно, что сумма 18 делится на 3. Число 165 при разложении на однозначные цифры с последующим сложением превращается в 12, которое может разделиться на три. Оба числа кратны одновременно 2 и 3, значит, кратны шести.
Определение отношения с делимостью на семь довольно сложное: число делится, если при удвоении последней цифры и полученной разности результат кратен семи или равен нулю.

Пример, трехзначное число 679 кратно 7. (Калькулятор выдал 97). Узнать можно так:
- 2*9=18.
- 67−18=49.
- 49:7=7.
Из примера видно, что удвоилось последнее число, затем получена разность, после чего — отношение-доказательство.
В классе было дано задание доказать, что число 497 делится на семь. Порядок решения:
- 2*7=14.
- 49−14=35.
- 35:7=5.
Найти признак делимости на 8 очень легко. Формулировка закона такова: последние три цифры должны быть 000 или 888. Легко можно произвести вычисления с 789000: оно делится на 8, так как оканчивается на 000. Множество 289673888 тоже кратно 8, поскольку заканчивается на 888.
Свойство при делителе 9 похоже на правило с 3. Формула делимости на 9 довольно простая: сумма цифр должна быть кратна девяти. Маленький пример: из 46980 возможно получить целое, 4+6+9+8+0= 27. Получившаяся сумма кратна 9. Еще одно задание: найти отношение с использованием признака кратности 9 при делимом 29565. Рассуждение: 2+9+5+6+5=27. Полученная сумма может разделиться на девять.
Разрядные единицы
Любое число можно разделить на разрядную единицу, если у него одинаковое или большее количество нулей в конце. Например, 5790 можно поделить на 10, так как в конце один ноль. Еще примеры:
- 4958700:100=49587.
- 374000:1000=374.
- 5781000:100=5781.
- 97430:10=9743.
Невозможно разделить 128700 на 1000, так как у разрядной единицы нулей больше, а также 237480 на 100 и другие подобные.
Делители от 11 и выше
Чтобы получилось деление на 11, необходимо сложить четные по счету номера, а затем нечетные, затем произвести вычитание. Если в процессе вычислений получился ноль или одиннадцать, то остатка не будет.
Онлайн-задание с ответом: 7535, 74019 и 50486.

Нечетные в первом случае 7 и 3, четные 5 и 5. Считаем:
- 7+3=10,
- 5+5=10,
- 10−10=0.
Четные во втором примере 4 и 1, нечетные — 7, 0, 9. Вычисление:
- 7+0+9=16.
- 4+1=5.
- 16−5=11.
В третьем примере нечетные 5, 4, 6, четные 0 и 8. Решаем:
- 5+4+6=15.
- 0+8=8.
- 15−8=7.
Ответ: в первом и втором примере десятых, сотых, тысячных и так далее не останется, а в третьем — останется.
Чтобы разделить на двузначный делитель 12, нужно произвести общие вычисления, характерные для делителей 3 и 4 одновременно. К примеру, 900 и 3432. Сначала следует разложить на слагаемые 9+0+0=9, значит, можно поделить на 3. В конце стоит два нуля — можно делить на 4. Проверка: 900:12=75. Первая часть задания решена, теперь делаем вторую: 3+4+3+2=12, 12:3=4. Таким образом проверяется кратность трем. Теперь четырем: в конце стоит 32, что указывает на кратность 4, значит, остатка не будет. Таким образом, оба примера кратны 12.

Дробь, кратная 13, разрешится без остатка, если последнюю цифру умножить на 4, после чего сложить число и последнюю цифру. Если полученная сумма кратна 13 или равно 0, то деление получится.
Например, 6942:
- 2*4=8.
- 694+8=702.
- 702:13=54.
Еще пример — 754:
- 4*4=16.
- 75+16=91.
- 91:13=7.
Признак делимости на составное число
Если делитель составной, необходимо его разложить на простые множители, которые не имеют общих кратных, кроме единицы. Пример: 15 раскладывается на 3 и 5. Любое неизвестное кратно 15, если одновременно кратно трем и пяти.
Также и с другим составным: 18 раскладывается на 2 и 9. Нельзя брать множители 3 и 6, так как они не простые, у них общее кратное 3. Например, 456 кратно трем, проверка: 4+5+6=15, также кратно 6 (при разложении на 2 и 3). Однако калькулятор выводит запятую. Если взять множители 2 и 9, будет видно, что двум — кратно, а девяти — нет, ведь сумма равна 15, которая не кратна 9.
Таблица кратных от 2 до 10
Для удобства школьникам и их родителям предлагается таблица признаков делимости чисел от 2 до 10. Она наглядно и кратко демонстрирует всю вышеизложенную теоретическую часть:
| Делимость на: | Признак числа: |
| 2 | Оканчивается четной цифрой: 0, 2, 4,6, 8 |
| 3 | Сумма цифр, их которой оно состоит, делится на 3 |
| 4 | Две последние цифры делятся на 4 |
| 5 | Окончание на 5 или 0 |
| 6 | Одновременная кратность 2 и 3 |
| 8 | Три последние цифры кратны 8 |
| 9 | Сумма цифр кратна 3 |
| 10 | Окончание равно нулю |
Вышеизложенное доказывает, что к любому натуральному числу можно подобрать простой или составной признак кратности. На практике выходит, что чем больше число, тем сложнее его признак. Часто не хочется тратить время на проверку делимости, ведь за этот промежуток уже можно выполнить само деление. Поэтому любой школьник может воспользоваться простейшими признаками делимости.
Источник
Математика
5 класс
Урок №39
Свойства делимости
Перечень рассматриваемых вопросов:
– свойства делимости;
– чётные и нечётные числа;
– кратность чисел.
Глоссарий по теме:
Деление – действие, обратное умножению.
Кратное натурального числа – это число, которое делится на данное натуральное число без остатка
Умножение – это арифметическое действие, в котором первое число повторяется в качестве слагаемого столько раз, сколько показывает второе число.
Обязательная литература
1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. ФГОС// С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 кл.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. //
И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.
Теоретический материал для самостоятельного изучения
Сегодня мы будем изучать свойства делимости, так как деление – это одно из основных арифметических действий в математике.
Для начала вспомним, что такое деление. Это действие, обратное умножению. Т. е. говорят, что натуральное число а делится нацело на натуральное число b, если существует число с, при умножении которого на число b получается число а. При дальнейших рассуждениях слова «натуральные», «нацело» будем опускать для краткости.
Прежде чем рассмотреть свойства делимости, введём определение кратного числа.
Кратное натурального числа – это число, делящееся на данное целое число без остатка.
Если а делится на b, то говорят ещё, что а кратно b, при этом a ≥ b.
Например, число36 кратно числу 12, т. к. 36 : 12 = 3.
Теперь рассмотрим свойства делимости.
Первое свойство. Если один из множителей делится на некоторое число, то и произведение делится на это же число.
Например, двадцать пять делится на пять, значит и произведение чисел двадцать пять и двенадцать делится на пять. Т.к. число двадцать пять можно разложить на множители пять и пять. И наш делитель пять входит в это произведение. Следовательно
это произведение делится на заданное число.
25 · 12 = (5 · 5) · 12 = 5 · (5 · 12)
Рассмотрим второе свойство. Оно заключается в том, что если первое число делится на второе, а второе делится на третье, то первое число делится на третье.
Например, 168 делится на 56, т. к. 168 – это результат произведения 56 и 3.
56 делится на 8, т. к. 56 – это результат произведения 7 и 8.
Следовательно, 168 делится на 8, т. к. 168 – это результат произведения трёх чисел – 8, 3 и 7. Если поделить 168 на 8, получится 21.
168 делится на 8, т. к. 168 : 8 = 8 · (3 · 7) : 8 = 21.
Рассмотрим третье свойство. Оно заключается в том, что если каждое из двух чисел делится на некоторое число, то их сумма и разность делятся на это число.
Например,
200 делится на 2, т. к. 200 – это произведение 2 и 100.
24 тоже делится на 2, т. к. 24 – это произведение 2 и 20.
Следовательно, 224 делится на 2, т. к. это число есть сумма 200 и 24, или сумма произведений чисел 2 и 100 и 2 и 12.
Используя распределительное свойство, получим произведение числа 2 на сумму чисел 100 и 12. Или, иначе говоря, произведение числа 2 и числа 112.
224 делится на 2, т. к.
224 = 200 + 24 = 2 · 100 + 2 · 12 = 2 · (100 + 12) = 2 · 112.
Теперь возьмём число 35. Оно делится на 5. Представим его как разность 100 и 65. Т. к. 100 – это произведение 5 и 20, а 65 – это произведение 5 и 13, то получим следующее выражение:
35 = 100 – 65 = 5 · 20 – 5 · 13 = 5 · (20 – 13) = 5 · 7.
35 – это разность 100 и 65, или разность произведений чисел 5 и 25 и 5 и 13. Используя распределительное свойство, получим произведение 5 и разности чисел 20 и 13. Выполнив действие вычитания, получим результат произведения чисел 5 и 7.
Рассмотрим четвёртое свойство. Оно заключается в том, что если одно из двух чисел делится на некоторое число, а другое на него не делится, то их сумма и разность не делятся на это число.
Например,
48 делится на 2, т. к. 48 = 2 · 24.
15 не делится на 2.
Следовательно, 48 + 15 и 48 – 15 не делятся на 2.
В противном случае это противоречило бы свойству три. Итак, сегодня мы познакомились со свойствами делимости и научились применять их к выражениям.
Занимательная задача
Решим занимательную задачу, основываясь на свойствах делимости, но с большим количеством слагаемых.
В цветочном магазине имеются 33 розы, 27 хризантем и 21 лилия. Возможно ли из них составить три одинаковых букета? Если да, то сколько цветов будет в каждом букете?
Решение:
Для решения задачи составим следующее выражение:
(33 + 27 + 21) : 3
Исходя из свойства 3 (если каждое из двух чисел делится на некоторое число, то их сумма и разность делятся на это число), мы можем разделить как два числа, так и все три числа на 3.
33 : 3 = 11
27 : 3 = 9
21 : 3 = 7
Все числа делятся на 3, следовательно, букет с одинаковым количеством цветов собрать можно. Теперь посчитаем, сколько цветов будет в каждом букете. Для этого найдём сумму следующих чисел
11 + 9 + 7 = 27 цветов
Ответ: можно составить букеты, в каждом будет 27 цветов
Тренировочные задания.
№ 1. Какие из чисел 28; 25; 23; 22 делятся на 14?
Решение: для решения задачи достаточно найти числа, кратные числу 14. Начнём проверку кратных с числа 2, т.к. при умножении 14 на 1 кратное будет само число 14;
14 · 2 = 28 – это число есть в условии;
14 · 3= 42 – это число уже больше тех, что даны по условию задачи. Следовательно, остальные числа не будут делиться на 4.
Ответ: 28.
№ 2. Делится ли сумма (54 + 12) на 9?
Решение: исходя из свойства 3 (если каждое из двух чисел делится на некоторое число, то их сумма и разность делятся на это число), проведём рассуждения для этого задания:
54 делится на 9, т. к. 54 = 9 · 6
12 не делится на 9, т. к. 12 = 4 · 3 = 2 · 2 · 3
Следовательно, (54 + 12) не делится на 9.
Ответ: сумма чисел не делится на 9.
Источник
Алгебра и начала математического анализа, 10 класс
Урок №7. Делимость. Свойства и признаки делимости.
Перечень вопросов, рассматриваемых в теме:
- наибольший общий делитель пары чисел;
- признаки делимости и метод математической индукции для доказательства делимости.
Глоссарий по теме
Натуральные числа – это числа, возникающие естественным образом при счете предметов.
Целые числа – это расширение множества натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел.
Число n – делитель числа m, делимое m – кратное числа n, а число q – частное от деления m на n.
Простое число – это натуральное число, у которого есть лишь два различающихся натуральных делителя – самого число и единица.
Взаимно простые числа – два натуральных числа, у которых есть лишь один общий делитель, единица.
Наибольший общий делитель (НОД) чисел n и m – самое большое из натуральных чисел, которые являются одновременно делителями натуральных чисел n и m.
Алгоритм Евклида – алгоритм для нахождения наибольшего общего делителя пары чисел.
Знакочередующаяся сумма – это сумма чисел, в которой каждый второй член помножен на –1.
Трехзначные грани числа – это числа, которые получены разбиением исходного числа на трехзначные числа, начиная с его конца.
Метод математической индукции – метод доказательства в математике, необходимый для доказательства истинности утверждения при всех натуральных числах, начиная с некоторого минимального.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е., Шабунин М.И., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2011.
Дополнительная литература:
Баданин А. С., Сизова М. Ю. Применение метода математической индукции к решению задач на делимость натуральных чисел // Юный ученый. — 2015. — №2. — С. 84-86.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Целое число
Целое число является основополагающим понятием арифметики и математики в целом. Однако их множество, пожалуй, выходит за грань обыденного понимания чисел. Долгое время человечество не использовало для описания явлений, например, отрицательные числа.
Обычно множество целых чисел определяется достраиванием множества натуральных чисел дополнительными элементами. Поэтому, перед тем, как дать определение целых чисел, необходимо ввести понятие натуральных чисел.
Натуральные числа – это числа, возникающие естественным образом при счете предметов.
Для иллюстрации множества натуральных чисел отметим их на числовой оси. Для этого построим луч с началом в произвольной точке. Отметим на нем отрезки единичной длины, левый конец которых совпадает с окончанием предыдущего отрезка, а началом первого из них является начало луча.
Поставим в соответствие каждой из точек, отмеченной на прямой, свой порядковый номер. Эти номера являются натуральными числами, возникающими при счете числа точек на луче (рис. 1).

Рисунок 1 – числовой луч
Число точек на луче бесконечно и каждой ставится в соответствие свое натуральное число.
Целые числа – это расширение множества натуральных чисел, получаемое добавлением к нему нуля и отрицательных чисел.
Дополним нашу числовую ось ненатуральными целыми числами. Отложим второй луч в противоположном первому направлении от точки начала первого луча. И также отложим на нем единичные отрезки (рис. 2)

Рисунок 2 – числовой луч
Добавим на ноль и отрицательные числа, чтобы получить иллюстрацию множества целых чисел (рис. 3).

Рисунок 3 – числовой луч
Делимость. Делитель и частное.
Определив натуральные и целые числа, мы можем через них дать понятие делимости чисел.
Целое число m делится на натуральное число n (или n делит m), если для числа m и числа n существует такое целое число q, что m = n · q.
Число n – делитель числа m, делимое m – кратное числа n, а число q – частное от деления m на n.
Например, целое число – 10 делится на натуральное число 5, так как для этих двух чисел существует целое число –2, такое, что –10 = 5 · –2. При этом –10 – кратное числа 5, 5 – делитель 10, а –2 является частным от деления 10 на 5.
Заметим, что делимость можно определить по-разному. Вместо натурального числа n в определении выше, можно было бы задать n как целое число. Однако мы будем придерживаться определения, введенного в данном уроке.
Часто рассматривают лишь делимость натуральных чисел, хотя по определению кратное в общем случае является целым числом.
Свойства делимости.
Перечислим некоторые свойства делимости:
1. Все целые числа делятся на единицу.
2. Каждое целое число, неравное нулю делится на натуральное число равное модулю от данного целого.
3. Все натуральные числа являются делителями нуля.
4. Если целое число a делится на натуральное число b и модуль числа a меньше b, то a равно нулю.
5. Если целое число a отлично от нуля и делится на натуральное число b, то модуль числа a не меньше числа b.
6. Единственный делитель единицы – сама единица.
7. Чтобы целое число a делилось на натуральное число b необходимо и достаточно, чтобы модуль числа a делился на b.
8. Пусть целое число a делится на натуральное число m, а число m в свою очередь делится на натуральное число k, тогда a делится на k (свойство транзитивности деления).
9. Если натуральные числа делятся друг на друга без остатка, то они равны.
Свойства делимости удобно использовать при доказательстве теорем и решении задач.
Взаимно простые числа.
Простое число – это натуральное число, у которого есть лишь два различающихся натуральных делителя – самого число и единица.
Перечислим некоторые первые простые числа в порядке их возрастания: 2, 3, 5, 7, 11, 13. Любое натуральное число можно представить в виде произведения простых чисел. Это называется факторизацией натурального числа.
Взаимно простые числа – два натуральных числа, у которых есть лишь один общий делитель, единица.
Наибольший общий делитель.
Наибольший общий делитель (НОД) чисел n и m – самое большое из натуральных чисел, которые являются одновременно делителями натуральных чисел n и m.
Например, для чисел 77 и 14 наибольший общий делитель равен 7: НОД (77, 14) = 7.
НОД чисел n и m равен 1 тогда и только тогда, когда числа n и m взаимно просты.
Делимость суммы и произведения.
Рассмотрим свойства делимости суммы разности и произведения чисел. Пусть a и b – целые числа, а m, n и k – натуральные числа.
1) Пусть оба числа a и b делятся на m, тогда числа a + b и a – b также делятся на m.
2) Пусть оба числа a и b делятся на m, тогда при любых k и n число k · a + n · b делится на m.
3) Пусть число a делится на m, а число b не делится на m, тогда числа a + b и a – b не делятся на m.
4) Пусть число a делится на m, а число b делится на n, тогда ab делится на mn.
5) Пусть число a делится на m и n, и при этом m и n – взаимно простые числа, тогда a делится на mn.
6) Пусть число a делится на m, тогда ak делится на mk.
Деление с остатком.
Натуральное число n можно представить в виде:
n = q · m + r ИЛИ n / m = q (остаток r)
где q – целое неотрицательное число (0, 1, 2, …), m – натуральное число, r – целое неотрицательное число, меньшее m (0, 1, 2, …, m – 1).
Число n называют делимым, m – делителем, q – (неполным) частным, r – остатком (от деления).
Например, число 23 представимо в виде: 23 = 2 · 10 + 3, где 23 – делимое, 10 – делитель, 3 – остаток.
Алгоритм Евклида.
Нахождение наибольшего общего делителя пары чисел может стать весьма сложной задачей. Для упрощения решения подобных примеров существует алгоритм Евклида.
Пусть a и b– натуральные числа, не равные одновременно нулю, и верна последовательность чисел
где каждое – это остаток от деления числа, предшествовавшего предыдущему числу, на предыдущее число:
ИЛИ (остаток )
ИЛИ (остаток )
ИЛИ (остаток )
ИЛИ (остаток )
…
ИЛИ (остаток rk)
…
ИЛИ(остаток rn)
ИЛИ (остаток 0)
То есть после первых двух шагов мы получаем последовательность остатков, делящихся друг на друга. При этом предпоследнее число делится на последнее нацело.
НОД(a, b), равен , то есть последнему ненулевому члену этой последовательности.
Признаки делимости.
Зачастую в задаче требуется ответить, делится ли число на определенное целое число.
Для начала введем вспомогательные понятия, необходимые для формулирования признаков делимости.
Знакочередующаяся сумма – это сумма чисел, в которой каждый второй член помножен на –1.
Например, знакочередующаяся сумма всех цифр, записанных от нуля до девяти равна:
0 – 1 + 2 – 3 + 4 – 5 + 6 – 7 + 8 – 9 = – 5.
Трехзначные грани числа – это числа, которые получены разбиением исходного числа на трехзначные числа, начиная с его конца.
Например, трехзначные грани числа 6579813 это 6, 579, 813.
Таблица 1 – Признаки делимости
Число n | Число a делится на число n тогда и только тогда, когда |
2 | последняя цифра числа a делится на 2 |
3 | сумма всех цифр числа a делится на 3 |
4 | число, составленное из двух последних цифр числа a, делится на 4 |
5 | число a оканчивается цифрой 0 или 5 |
7 | знакочередующаяся сумма трехзначных граней числа a делится на 7 |
8 | число, составленное из трех последних цифр числа a, делится на 8 |
9 | сумма всех цифр числа a делится на 9 |
10 | число a оканчивается цифрой 0 |
11 | знакочередующаяся сумма цифр числа a делится на 11 |
13 | знакочередующаяся сумма трехзначных граней числа a делится на 13 |
25 | число, составленное из двух последних цифр числа a, делится на 25 |
Заметим, что в формулировке признаков фигурирует выражение «тогда и только тогда». Это означает, что эти признаки являются также и свойствами чисел, которые однозначно делятся на одно из перечисленных чисел.
Метод математической индукции для доказательства делимости.
Схема метода:
1. Базис индукции.
Доказываем справедливость утверждения для наименьшего из натуральных чисел, при котором утверждение верно.
2. Индукционное предположение.
Предполагаем, что утверждение верно для некоторого натурального значения k.
3. Шаг индукции (индукционный переход).
Доказываем, что утверждение справедливо для значения k+1.
4. Вывод.
Если утверждение оказалось справедливым при каждом доказательстве в предыдущих шагах, то утверждение верно для любого натурального числа n.

Примеры и разбор решения заданий тренировочного модуля
Задача №1
Условие:
Найдите среди чисел пары взаимно простых.
65, 30, 110, 1001, 273, 35, 14, 26
Решение:
Для начала найдем среди представленных чисел группы, которые имеющие общий делитель не равный единице и которые точно не могут быть взаимно простыми друг для друга.
По признаку делимости на 2, число делится на 2 тогда и только тогда, когда его последняя цифра является четной. Значит, можно выделить первую группу чисел: 30, 110, 14, 26. Каждое из них делится на 2.
По признаку делимости на 5, число делится на 5 тогда и только тогда, когда его последняя цифра равна 5 или 0. Значит, можно выделить вторую группу чисел: 65, 30, 110, 35. Каждое из них делится на 5.
По признаку делимости на 7, число делится на 7 тогда и только тогда, когда знакочередующаяся сумма трехзначных граней этого числа делится на 7. Значит, можно выделить третью группу чисел: 1001, 273, 35, 14. Каждое из них делится на 7.
По признаку делимости на 13, число делится на 13 тогда и только тогда, когда знакочередующаяся сумма трехзначных граней этого числа делится на 13. Значит, можно выделить четвертую группу чисел: 65, 1001, 273, 26. Каждое из них делится на 13.
Очевидно, что внутри одной группы не могут находиться пары взаимно простых чисел. Поэтому искать такие пары нужно среди чисел, не принадлежащих одной группе. Начнем с 65. Единственным числом, которое остается после исключения из данных чисел всех, кто находится с ним в одной из групп, является 14.
Проведем аналогичные действия со всеми остальными данными числами, исключая найденные взаимно простые пары.
Получим возможные пары:
(65; 14)
(30; 273) или (30; 1001)
(110; 1001) или (110; 273)
(35; 26)
Чтобы быть уверенными в найденной паре, необходимо удостоверится, что НОД пары равен 1.
Проверим, действительно ли 65 и 14 являются взаимно простыми. Разложим каждое из них на простые множители. 65 = 5 · 13, 14 = 7 · 2. НОД(65, 14) = 1, они действительно взаимно простые.
Проверим, действительно ли 35 и 26 являются взаимно простыми. Разложим каждое из них на простые множители. 35 = 5 · 7, 26 = 13 · 2. НОД(35, 26) = 1, они действительно взаимно простые.
Проверим пару (30; 273). По признаку делимости на 3 они оба делятся на это число. Значит, они не взаимно простые.
Проверим, действительно ли 30 и 1001 являются взаимно простыми. Разложим каждое из них на простые множители. 30 = 3 · 2 · 5, 1001 = 13 · 11· 7. НОД(30, 1001) = 1, они действительно взаимно простые.
Осталось проверить пару (110; 273). Разложим каждое из них на простые множители. 110 = 2 · 5 · 11, 273 = 3 · 91 = 3 · 7 · 13. НОД(110, 273) = 1, они действительно взаимно простые.
Ответ: (65; 14), (30; 1001), (110; 273), (35; 26).
Задача №2.
Условие:
Найдите НОД(2457, 1473).
Решение:
Решим задачу с помощью алгоритма Евклида.
Составим последовательность, включающую оба эти числа и остатки от деления предыдущих членов последовательности друг на друга:
2457 = 1 · 1473 + 984
1473 = 1 · 984 + 489
984 = 2 · 489 + 6
489 = 81 · 6 + 3
6 = 3 · 2
Последний ненулевой член этой последовательности оказался равен 3. Следовательно, НОД(2457, 1473) = 3.
Ответ: НОД(2457, 1473) = 3.
Задача №3.
Условие:
Определите, делится ли число 17943646 на 7.
Решение:
Для начала разобьем это число на грани: 17|943|646. Получили числа 17, 943, 646. Найдем их знакочередующуюся сумму: 17 – 943 + 646 = –280. Число –280 делится на 7 нацело. Следовательно, по признаку делимости числа на 7 число 17943646 также делится на 7 нацело.
Ответ: число 17943646 делится на 7 без остатка.
Задача №4.
Условие:
Докажите делимость + 6n – 10 на 18при любом натуральном n.
Решение:
Воспользуемся методом математической индукции для решения задачи.
1. Проверим справедливость утверждения при n = 1:
+ 6 – 10 = 10 – 10 = 0
Ноль делится на любое натуральное число, значит на 18 тоже. Утверждение справедливо при n = 1.
2. Предположим, что утверждение верно для некоторого натурального значения k. Тогда + 6k – 10 делится на 18. То есть, по определению: + 6k – 10 = 18 · m, где m – целое число.
3. Рассмотрим выражение при n = k +1.
+ 6(k + 1) – 10 = 4 ⋅ + 6k + 6 – 10 = 4 ·+ 6k – 4
Воспользуемся нашим предположением о верности рассматриваемого утверждения для значения k:
+ 6k – 10 = 18m, следовательно = –6k + 10 + 18m.
Подставим полученное значение для в выражение при n = k + 1:
+ 6(k + 1) – 10 = 4(–6k + 10 + 18m) + 6k – 4 = –24k + 40 + 4 · 18m + 6k – 4 = –18k + 4 · 18m + 36 = 18(–k + 4m + 2) = 18 · q, где q – некоторое целое число. Из этой записи следует, что + 6(k + 1) – 10 делится на 18 по определению. Следовательно, данное утверждение верно при значении n = k + 1.
4. Утверждение оказалось справедливым при наименьшем натуральном числе n = 1 и при n = k + 1 с условием его верности при n = k. По методу математической индукции следует, утверждение справедливо при любом натуральном n. Что и требовалось доказать.
Источник
