Какие свойства биологической ткани моделируют элементы эквивалентной схемы
Электрические свойства биологических тканей моделируются сочетанием элементов, обладающих омическими и емкостными свойствами. Эти свойства можно моделировать с помощью эквивалентных электрических схем. Рассмотрим три из них, рис. 17.
Схема I не совсем удовлетворительна, т.к. содержит бесконечно большое сопротивление постоянному току (емкость не проводит постоянный ток), чего не наблюдается в тканях организма. Поэтому при низкой частоте схема I даст существенные отклонения расчетных значений импеданса (полного сопротивления) от реального импеданса биоткани. В схеме // при увеличении частоты тока ω емкостное сопротивление стремится к нулю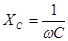 
поэтому импеданс схемы также стремится к пулю. Это противоречит опыту.
У живых объектов импеданс уменьшается по мере увеличения частоты только до определенного значения. Для живых тканей характерно более сложное сочетание параллельного и последовательного соединений элементов, например, схема ///.
В состоянии покоя реактивное сопротивление ткани носит только емкостный характер, при возбуждении ткань приобретает индуктивные свойства и обладает индуктивным сопротивлением
XС =ω L.
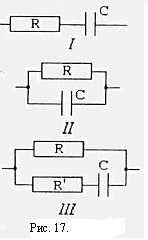
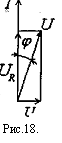При анализе электрических свойств ткани рассматриваем только состояние покоя. Найдем импеданс Z простейшей эквивалентной электрической схемы /, рис. Векторная диаграмма имеет вид, показанный на рис.17. Общее напряжение равно
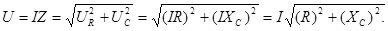
Следовательно, импеданс цепи равен
Угол сдвига фазы между током I и напряжением U найдем из условия.
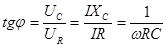
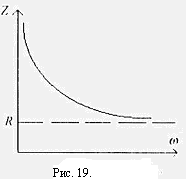На рис.19. показана зависимость Z импеданса эквивалентной электрической схемы / (рис.17.) от частоты, построенная но формуле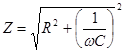 
Как видно из рис. 19., импеданс цепи монотонно падает с увеличением частоты электрического тока, постепенно приближаясь к активному сопротивлению R..
Величины логарифмов импеданса и относительной диэлектрической проницаемости можно считать по модулю примерно пропорциональными друг другу.
Зависимость импеданса (или относительной диэлектрической проницаемости) биологических тканей от частоты электрического тока называется дисперсией импеданса (или относительной диэлектрической проницаемости), а график этой зависимости дисперсионной кривой.
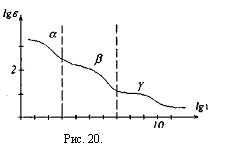
В отличие от зависимости импеданса от частоты электрического тока для эквивалентной электрической схемы биологической ткани, реальная дисперсионная кривая, например, скелетной мышцы, немонотонно падает с увеличением частоты, рис.20.
При действии на ткани организма переменного электрического тока или переменного электрического поля наблюдаются три области дисперсии. Область а – дисперсии.
Наблюдается до частот 1кГц (lgv≈3)
В низкочастотной части спектра области а- дисперсии электрический ток течет практически только по межклеточной жидкости, т.к. сопротивление мембран клеток очень велико. В высокочастотной части спектра импеданс падает за счет снижения емкостного сопротивления мембран клеток Хс =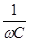 
Возникает ток смещения, текущий через мембрану.
Область β- дисперсии.Наблюдается до частот I04 кГц (Igv≈3 – 7)
За счет увеличения частоты переполяризации мембран клеток снижается емкостное сопротивление ткани. Переполяризация рассматривается относительно пулевого уровня потенциала па мембране, за который принят потенциал покоя.
Затраты энергии на поляризацию и нереполяризацию клеточных структур (мембран, белковых молекул, молекул воды, атомов и т.д.) определяют импеданс ткани. Снижение этих затрат приводит к снижению импеданса биоткани.
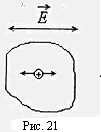Многие ионы внутри клеток, рис.21, при такой частоте колебаний напряженности электрического поля 
не успевают дойти до клеточных и внутриклеточных мембран. Для них сопротивление мембран роли не играет.
В высокочастотной области β- дисперсии существенное значение приобретает структурная поляризация и переполяризация крупных, в частности белковых молекул. Структурная поляризация заключается в том, что внутри молекулы, под действием электрического поля, смещаются ионы и ионные группы, входящие в состав молекул, что влияет на функциональные свойства белков.
Область γ дисперсии. Наблюдается до частот 107 кГц (Igv =• 7 – 10).
За счет высокой частоты колебаний электрического тока, емкостное сопротивление мембран очень мало и они не представляют большого препятствия для переменного тока. Поэтому сопротивление биоткани в общем мало.
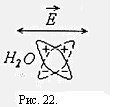
В низкочастотной части спектра области γ- дисперсии уменьшение диэлектрической проницаемости обусловлено постепенным ослаблением ориентационной переполяризации дипольных молекул воды, рис.22. В этой области важный вклад в импеданс ткани вносит структурная поляризация крупных молекул. Энергия электрического тока с увеличением частоты все меньше теряется на переориентацию молекул воды и структурную переполяризацию крупных молекул, поэтому уменьшается импеданс ткани.
В высокочастотной части спектра γ – дисперсии молекулы воды под действием переменной напряженности Е почти не переполяризуются. Уровень электрического сопротивления определяется электронной переполяризацией атомов, т. с. возникновением переменных атомных диполей, рис.23.
Источник
Полная цепь переменного тока – это цепь из генератора, а также R, C, и L элементов, взятых в разных сочетаниях и количествах.
Для разбора проходящих в электрических цепях процессов используют полные последовательные и параллельные цепи.
Последовательная цепь – это такая цепь, где все элементы могут быть соединены последовательно, один за другим.
В параллельной цепи R, C, L элементы соединены параллельно.
Особенности полной цепи:
1.Соблюдается закон Ома
2.Полная цепь оказывает переменному току сопротивление. Это сопротивление называется полным (мнимым, кажущимся) или импедансом.
3.Импеданс зависит от сопротивления всех элементов цепи, обозначается Z и вычисляется не простым, а геометрическим (векторным) суммированием. Для последовательно соединенных элементов формула импеданса имеет следующее значение:
здесь:
Z – импеданс последовательной цепи,
R – активное сопротивление,
XL – индуктивное и XC – ёмкостное сопротивление,
L – индуктивность катушки (генри),
C – ёмкость конденсатора (фарад).
Так как ёмкостное и индуктивное сопротивления дают для напряжения сдвиг фаз в противоположном направлении, возможен случай, когда XL = XC. При этом алгебраическая сумма модулей будет равна нулю, а импеданс – наименьшим.
Состояние, при котором в цепи переменного тока ёмкостное сопротивление равно индуктивному, называется резонансом напряжения. Частота, при которой XL = XC, называется резонансной частотой. Эту частоту np можно определить по формуле Томсона:
4.Особенности импеданса живой ткани и её эквивалентная электрическая схема.
При пропускании тока через живую ткань, её можно рассматривать как электрическую цепь, состоящую из определенных элементов.
Экспериментально установлено, что это цепь обладает свойствами активного сопротивления и ёмкости. Это доказывается выделением тепла и уменьшением полного сопротивления ткани с возрастанием частоты. Свойств индуктивности у живой ткани практически не обнаруживается. Таким образом, живая ткань представляет собой сложную, но не полную электрическую цепь.
Импеданс живой ткани можно рассматривать как для последовательного, так и для параллельного соединения её элементов.
При последовательном соединении токи через элементы равны, общее приложенное напряжение будет векторной суммой напряжений на R и C элементах и формула импеданса последовательной цепи будет иметь вид:
Z_ – импеданс последовательной цепи,
R – её активное сопротивление,
XC – ёмкостное сопротивление.
При параллельном соединении напряжения на R и C элементах равны, общий ток будет векторной суммой токов каждого элемента, а фомула импеданса будет следующей:
Теоретические формулы импеданса живой ткани при параллельном и последовательном соединении её элементов от экспериментальных отличаются следующим:
1.При последовательной схеме соединения практические данные дают большие отклонения на низких частотах.
2.При параллельной схеме эти измерения показывают конечное значение Z, хотя теоретически оно должно стремиться к нулю.
Эквивалентная электрическая схема живой ткани – это условная модель, приближенно характеризующаяживую ткань, как проводник переменного тока.
Схема позволяет судить:
1.Какими электрическими элементами обладает ткань
2.Как соединены эти элементы.
3.Как будут меняться свойства ткани при изменении частоты тока.
В основе схемы лежат три положения:
1.Внеклеточная среда и содержимое клетки есть ионные проводники с активным сопротивлением среды Rср и клетки Rк.
2.Клеточная мембрана есть диэлектрик, но не идеальный, а с небольшой ионной проводимостью, а, следовательно, и сопротивлением мембраны Rм.
3.Внеклеточная среда и содержимое клетки, разделённые мембраной, являются конденсаторами См определенной ёмкости (0,1 – 3,0 мкФ/см2).
Если в качестве модели живой ткани взять жидкую тканевую среду – кровь, содержащую только эритроциты, то при составлении эквивалентной схемы нужно учитывать пути электрического тока.
Их два:
1.В обход клетки, через внеклеточную среду.
2.Через клетку.
Путь в обход клетки представлен только сопротивлением средыRср.
Путь через клетку сопротивлением содержимого клетки Rк, а также сопротивлением и ёмкостью мембраны.Rм, См.
Если заменить электрические характеристики соответствующими обозначениями, то получим эквивалентные схемы разной степени точности:
Схема Фрике (ионная проводимость не
учитывается).
Схема Швана (ионная проводимость учитывается в виде сопротивления мембраны)
Обозначения на схеме:
Rcp – активное сопротивление клеточной среды
Rk – Сопротивление клеточного содержимого
Cm – ёмкость мембраны
Rm – сопротивление мембраны.
Анализ схемы показывает, что при увеличении частоты тока проводимость клеточных мембран увеличивается, а полное сопротивление тканевой среды уменьшается, что соответствует практически проведенным измерениям.
Источник
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса – ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший “Салат из свеклы с чесноком”
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека – Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков – Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) – В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Изучение импеданса живой биологической ткани
Цель работы:1. Изучить зависимость импеданса биологической ткани от частоты переменного тока.
2. Определить сдвиг фаз между силой тока и напряжением при прохождении переменного тока через живую ткань.
3. Рассчитать и построить электрическую эквивалентную схему.
Литература
1. [1], §§ 18.2 – 18.4;
2. [2], §§ 43, 44, 144;
3. [3], стр. 217-230.
Вопросы входного контроля
1. Что такое электрический ток? Что является носителями тока в проводниках и растворах электролитов?
2. Закон Ома для участка цепи.
3. От каких величин зависит сопротивление проводника?
4. Как вычислить общее сопротивление цепи при последовательном, параллельном, смешанном соединении?
5. Почему постоянный ток не проходит по цепи при наличии в ней конденсатора?
6. Что происходит с конденсатором при подключении к нему источника постоянного тока?
7. Виды электрических сопротивлений в цепи переменного тока.
8. Как вычисляется емкостное сопротивление?
9. Как вычисляется полное сопротивление цепи переменного тока при последовательном соединении основных ее элементов?
10. Закон Ома для полной цепи.
11. Принципы построения векторной диаграммы токов и напряжений.
12. Как построить векторную диаграмму токов и напряжений для последовательного и параллельного соединения резистора и конденсатора?
13. Что такое импеданс живой ткани?
14. Какие виды сопротивлений можно выделить в живой биологической ткани?
15. Почему в биологических тканях нет элементов, аналогичных катушке индуктивности?
16. Что такое эквивалентная электрическая схема?
17. Какие свойства биологической ткани моделируют элементы эквивалентной схемы?
18. Как объяснить вид частотной зависимости импеданса живой ткани?
Краткая теория
Электрический ток представляет собой направленное движение заряженных частиц под действием электрического поля. Такими частицами могут быть электроны или положительные и отрицательные ионы.
В биологических объектах чисто электронная проводимость отсутствует, т.к. они в основном представляют собой или диэлектрики, или растворы электролитов (кровь, цитоплазма, различные тканевые жидкости). Особенностью биологических жидкостей является то, что в их состав, помимо растворов электролитов, входят белки и жиры, поэтому их удельное сопротивление постоянному току достаточно велико. Кроме того, на электрические свойства тканей и клеток значительное влияние оказывают клеточные мембраны.
Измерение электросопротивления тканей и органов представляет собой значительную трудность по следующим причинам:
– биологические объекты имеют разную конфигурацию, а применение формулы предполагает наличие однородного электрического поля между электродами;
– ткани и органы неоднородны по своему составу, а ток идет преимущественно по тем участкам, сопротивление которых меньше, поэтому измерять сопротивление ткани в целом крайне трудно, а порой невозможно;
– физические параметры живых существ не остаются постоянными с течением времени, они изменяются как в связи с физиологическими процессами, так и под действием протекающего тока, поэтому следует учитывать, что каждое предыдущее измерение, раздражая объект, может оказывать влияние на результат последующего измерения.
Если учесть все вышеуказанные факторы и, соблюдая предосторожности, измерить ток в какой-либо ткани, то окажется, что при постоянном напряжении на электродах сила тока меняется со временем. Уменьшение тока может произойти в сотни раз, и лишь после этого устанавливается какое-то постоянное значение тока. Резкое уменьшение силы тока в биологических объектах, а, следовательно, резкое возрастание их электросопротивления после замыкания электрической цепи объясняется поляризационными эффектами.
При рассмотрении цепей переменного тока общее сопротивление может быть представлено омическим, емкостным и индуктивным сопротивлением в различных их сочетаниях. В биообъектах, как в проводящей структуре, индуктивность отсутствует, и величина полного сопротивления определяется только активным и емкостным сопротивлением. В сочетании они могут быть представлены в виде так называемой эквивалентной цепи (рис. 1).
Рис. 1. Эквивалентная электрическая схема биологического объекта.
Емкостное сопротивление ХС биологической ткани переменному току зависит от емкостных свойств клеточных мембран и частоты тока:
Последовательно с емкостью в цепь включено активное сопротивление RК определяемое сопротивлением клеточной цитоплазмы. Помимо клетки, ток проходит и по внеклеточной жидкости, и поэтому все внутриклеточные сопротивления шунтируются сопротивлением внеклеточной среды RВ.
При низких частотах поляризационные эффекты почти также велики, как при постоянном токе; соответственно RК и ХС имеют большое значение и практически весь ток пойдет по шунтирующему сопротивлению RВ. Если же сечение межклеточных промежутков невелико, то сопротивление RВ возрастает и измеряемое полное сопротивление будет в основном определяться величиной RК. Поскольку RК зависит от проницаемости мембран, то величина сопротивления объекта, измеренная на низких частотах, в ряде случаев может служить мерой проницаемости клеточных мембран. При возрастании частоты переменного тока поляризационные эффекты уменьшаются, соответственно уменьшается величина ХС. При частотах порядка нескольких МГц поляризация мембран почти исчезает и величиной ХС при расчете полного сопротивления можно пренебречь. Таким образом, полное сопротивление Z, измеренное на высоких частотах, будет равно
,
так как оно будет определяться параллельно соединенными сопротивлениями электролитов внутри и вне клетки. Отсюда следует, что высокочастотное сопротивление биообъектов может служить мерой концентрации в них свободных ионов.
Таким образом, электросопротивление (или электропроводность) тесно связано как со свойствами клеточных мембран, так и со свойствами клеточных и межклеточных жидкостей. Как было показано выше, измерение удельного сопротивления у живых объектов представляет большие трудности, однако для диагностических целей это и не требуется. Получать сведения о явлениях, происходящих в тканях, можно, наблюдая за относительным изменением их электросопротивления между электродами любой формы, что широко применяют в медицине, для диагностики воспалительных процессов.
Весьма важные сведения о состоянии биологических объектов дают дисперсионные кривые, т.е. графики зависимости полного сопротивления ткани от частоты переменного тока (рис. 2). Такая зависимость присуща только живым тканям; при пропускании переменного тока через обычные растворы электролитов дисперсия электросопротивления не наблюдается. Причина дисперсии заключается в том, что на величину электросопротивления при постоянном токе или при низких частотах значительное влияние оказывает макроструктурная поляризация. Поскольку при увеличении частоты переменного тока уменьшаются пограничные поляризационные эффекты, это ведет к уменьшению полного сопротивления ткани, и дисперсионная кривая обладает значительной крутизной (рис. 2, кривая 1).
Рис. 2. Зависимость полного сопротивления растительной ткани от частоты переменного тока (кривая дисперсии):
1 – для здоровой ткани;
2 – для ткани после кратковременного нагревания в горячей воде;
3 – для той же ткани после ее кипячения (т.е. для неживой ткани).
При повреждении ткани возрастает проницаемость клеточных мембран, что приводит к уменьшению RП и СП и, следовательно, к уменьшению полного сопротивления на низких частотах. Поэтому кривая 2 на рисунке 2 обладает меньшей крутизной. При отмирании ткани поляризация на границах раздела практически исчезает и зависимость электросопротивления от частоты отсутствует, так как остается лишь активное сопротивление (рис. 2, кривая 3). Таким образом, по крутизне дисперсионной кривой можно судить о жизнеспособности той или иной ткани, что имеет большое значение, когда эта ткань предназначена для трансплантации.
Частотные зависимости электросопротивления сходны для многих тканей, однако величина полного сопротивления разных тканей различна. Зона дисперсии электросопротивления обычно находится в пределах от 100Гц до 100МГц.
Имеет также диагностическое значение измерение угла сдвига фаз j между током и напряжением. Этот угол для биообъектов довольно большой, что указывает на значительную долю емкостного сопротивления. Так для кожи человека на частоте 1кГц j=550¸570. При патологии величина j изменяется, что также может служить для целей диагностики.
Практическая часть
Задание 1.Измерить импеданс живой ткани для различных частот переменного тока.
Приборы и оборудование: генератор синусоидального напряжения, 2 милливольтметра, постоянный резистор, 2 электрода, соединительные провода, прокладки, физраствор.
Описание метода и схемы опыта
Измерение импеданса участка кожи предплечья человека производится косвенным методом. Электрическая цепь для проведения измерений представлена на рис. 3.
Электроды Э1 и Э2 помещаются на участок живой ткани с общим сопротивлением Z.
Рис. 3.
По закону Ома сила тока в цепи , где U – напряжение на выходе генератора; R – сопротивление резистора; Z – импеданс живой ткани. Если выходное напряжение поддерживать неизменным, то при постоянном значении R величина силы тока будет зависеть от величины импеданса Z. Поэтому, зная величину силы тока в цепи, можно судить о величине импеданса: .
Ток, проходящий через резистор R равен общему току в цепи. Его величину можно вычислить, измерив падение напряжения Ui на этом резисторе: . Тогда – получили формулу для расчета величины импеданса, измеренного данным методом.
Ход выполнения задания
1. Определить величину сопротивления постоянного резистора при помощи мультиметра (в режиме омметра).
2. Укрепить электроды на предплечье на расстоянии 10см друг от друга, подложив под них прокладки, смоченные физраствором. На протяжении всего опыта положение электродов не изменять.
3. Определить при помощи мультиметра величину сопротивления участка кожи предплечья постоянному току Z0.
4. Переключить мультиметр в режим измерения переменного напряжения.
5. Авометр (тестер) переключить в режим измерения переменного напряжения, выбрав предел измерения таким образом, чтобы было удобно измерять напряжения порядка 0,2-0,4В.
6. Собрать схему измерения импеданса участка кожи предплечья (рис. 3).
7. Установить на генераторе при помощи переключателей «частота» и «множитель» частоту выходного сигнала 20Гц.
8. Показать собранную схему преподавателю или лаборанту.
9. Включить схему в сеть и установить напряжение на выходе генератора равное 300мВ. Помните, что величина этого напряжения должна поддерживаться неизменной на протяжении выполнения всего задания.
10. Зарегистрировать значение напряжения Ui на резисторе R (показание мультиметра). Данные занести в таблицу 1.
Таблица 1.
| № | n | lgn | Ui | Z | lgZ |
| Гц | мВ | кОм | |||
… | 1.3 |
11. Повторить опыт 8-10 раз для различных значений частот, изменяя ее в пределах от 20Гц до 10000Гц.
12. Отключить схему от сети. Не снимая электродов с предплечья, отсоединить их от схемы.
13. Используя расчетную формулу, вычислить значение импеданса Z для различных частот переменного тока. Данные занести в таблицу.
14. Для построения графика зависимости импеданса от частоты вычислить логарифмы значений частоты и импеданса.
Построить график Z=f(n), используя логарифмические шкалы для координатных осей (рис. 4).
Рис. 4.
Задание 2.Рассчитать и смоделировать эквивалентную электрическую схему.
Приборы и оборудование: 1. Оборудование, перечисленное в первом задании.
2. Модель эквивалентной схемы с магазином конденсаторов и переменными сопротивлениями.
Источник