Какие свойства арифметического квадратного корня

Данная статья представляет собой совокупность детальной информации, которая касается темы свойства корней. Рассматривая тему, мы начнем со свойств , изучим все формулировки и приведем доказательства. Для закрепления темы мы рассмотрим свойства n-ой степени.

Свойства корней

Мы поговорим о свойствах.

Свойство умноженных чисел a и b, которое представляется как равенствоa·b=a·b. Его можно представить в виде множителей, положительных или равных нулю a1, a2, …, ak как a1· a2· …· ak=a1· a2· …· ak;
из частного a:b= a:b, a≥0, b>0, он также может записываться в таком виде ab=ab;
Свойство из степени числа a с четным показателем a2·m=am при любом числе a, например, свойство из квадрата числа a2=a.

В любом из представленных уравнений можно поменять части до и после знака тире местами, например, равенство a·b=a·b трансформируется как a·b=a·b. Свойства для равенства часто используются для упрощения сложных уравнений.

Доказательство первых свойств основано на определении квадратного корня и свойствах степеней с натуральным показателем. Чтобы обосновать третье свойство, необходимо обратиться к определению модуля числа.

Первым делом, необходимо доказать свойства квадратного корня a·b=a·b. Согласно определению , необходимо рассмотреть, что a·b – число, положительное или равное нулю, которое будет равно a·bпри возведениив квадрат. Значение выражения a·b положительно или равно нулю как произведение неотрицательных чисел. Свойство степени умноженных чисел позволяет представить равенство в виде (a·b)2=a2·b2. По определению квадратного корня a2=a и b2=b, то a·b2=a2·b2=a·b.

Аналогичным способом можно доказать, что из произведения k множителей a1, a2, …, ak будет равняться произведению квадратных корней из этих множителей. Действительно, a1·a2· …· ak2=a12· a22· …· ak2=a1· a2· …· ak.

Из этого равенства следует, что a1· a2· …· ak=a1· a2· …· ak.

Рассмотрим несколько примеров для закрепления темы.

Пример 1

3·525=3·525, 4,2·1312=4,2·1312 и 2,7·4·1217·0,2(1)=2,7·4·1217·0,2(1).

Необходимо доказать свойство арифметического квадратного корня из частного: a:b=a:b, a≥0, b>0. Свойство позволяет записать равенство a:b2=a2:b2, а a2:b2=a:b, при этом a:bявляется положительным числом или равно нулю. Данное выражение и станет доказательством.

Например, 0:16=0:16, 80:5=80:5 и 30,121=30,121.

Рассмотрим свойство квадратного корня из квадрата числа. Его можно записать в виде равенствакак a2=aЧтобы доказать данное свойство, необходимо подробно рассмотреть несколько равенств при a≥0 и при a<0.

Очевидно, что при a≥0 справедливо равенство a2=a. При a<0 будет верно равенство a2=-a. На самом деле, в этом случае −a>0 и (−a)2=a2. Можно сделать вывод, a2=a, a≥0-a, a<0=a. Именно это и требовалось доказать.

Рассмотрим несколько примеров.

Пример 2

52=5=5 и -0,362=-0,36=0,36.

Доказанное свойство поможет дать обоснованиеa2·m=am, где a – действительное, а m –натуральное число. Действительно, свойство возведения степени позволяет заменить степень a2·m выражением (am)2, тогда a2·m=(am)2=am.

Пример 3

38=34=34 и (-8,3)14=-8,37=(8,3)7.

Свойства корня n-ой степени

Для начала необходимо рассмотреть основные свойства корней n-ой степени:

Свойство из произведения чисел a и b, которые положительны или равны нулю, можно выразить в качестве равенства a·bn=an·bn, данное свойство справедливо для произведения k чисел a1, a2, …, ak как a1· a2· …·akn=a1n· a2n· …·akn;
из дробного числа обладает свойством abn=anbn, где a – любое действительное число, которое положительно или равно нулю, а b – положительное действительное число;
При любом a и четных показателях n=2·m справедливо a2·m2·m=a, а при нечетных n=2·m−1 выполняется равенство a2·m-12·m-1=a.
Свойство извлечения из amn=an·m, где a – любое число, положительное или равное нулю, n и m – натуральные числа, это свойство также может быть представлено в виде …ankn2n1=an1·n2…·nk;
Для любого неотрицательного a и произвольных n и m, которые являются натуральными, также можно определить справедливое равенство amn·m=an;
Свойство степени n из степени числа a, которое положительно или равно нулю, в натуральной степени m, определяемое равенством amn=anm;
Свойство сравнения , которые обладают одинаковыми показателями: для любых положительных чисел a и b таких, что a<b, выполняется неравенство an<bn;
Свойство сравнения , которые обладают одинаковыми числами под корнем: если m и n – натуральные числа, что m>n, тогда при 0<a<1 справедливо неравенство am>an, а при a>1 выполняется am<an.

Равенства, приведенные выше, являются справедливыми, если части до и после знака равно поменять местами. Они могут быть использованы и в таком виде. Это зачастую применяется во время упрощения или преобразовании выражений.

Доказательство приведенных выше свойств корня основывается на определении, свойствах степени и определении модуля числа. Данные свойства необходимо доказать. Но все по порядку.

Первым делом докажем свойства корня n-ой степени из произведения a·bn=an·bn. Для a и b, которые являютсяположительными или равными нулю, значение an·bn также положительно или равно нулю, так как является следствием умножения неотрицательных чисел. Свойство произведения в натуральной степени позволяет записать равенство an·bnn=ann·bnn. По определению корня n-ой степени ann=a и bnn=b, следовательно, an·bnn=a·b. Полученное равенство – именно то, что и требовалось доказать.

Аналогично доказывается это свойство для произведения k множителей: для неотрицательных чисел a1, a2, …, an выполняется a1n· a2n· …· akn ≥0 .

Приведем примеры использования свойства корня n-ой степени из произведения: 5·2127=57·2127 и 8,34·17,(21)4·34·574=8,3·17,(21)·3·574.

Докажем свойство корня из частного abn=anbn. При a≥0 и b>0выполняется условие anbn≥0, а anbnn=annbnn=ab.

Покажем примеры:

Пример 4

8273=83273 и 2,310:2310=2,3:2310.

Для следующего шага необходимо доказать свойстваn-ой степени из числа в степени n. Представим это в виде равенства a2·m2·m=a и a2·m-12·m-1=a для любого действительного a и натурального m. При a≥0 получаем a=a и a2·m=a2·m, что доказывает равенство a2·m2·m=a, а равенство a2·m-12·m-1=a очевидно. При a<0 получаем соответственно a=-a и a2·m=(-a)2·m=a2·m. Последняя трансформация числа справедлива согласно свойству степени. Именно это доказывает равенство a2·m2·m=a, а a2·m-12·m-1=a будет справедливо, так как за нечетной степени рассматривается -c2·m-1=-c2·m-1 для любого числа c, положительного или равного нулю.

Для того, чтобы закрепить полученную информацию, рассмотрим несколько примеров с использованием свойства:

Пример 5

744=7=7, (-5)1212=-5=5, 088=0=0, 633=6 и (-3,39)55=-3,39.

Докажем следующее равенство amn=an·m. Для этого необходимо поменять числа до знака равно и после него местами an·m=amn. Это будет означать верная запись . Для a, которое является положительнымили равно нулю, из вида amn является числом положительным или равным нулю. Обратимся к свойству возведения степени в степень и определению . С их помощью можно преобразовать равенства в виде amnn·m=amnnm=amm=a. Этим доказано рассматриваемое свойство корня из корня.

Аналогично доказываются и другие свойства. Действительно, …ankn2n1n1·n2·…·nk=…ankn3n2n2·n3·…·nk=…ankn4n3n3·n4·…·nk=…=anknk=a.

Например,735=75·3 и 0,00096=0,00092·2·6=0,000924.

Докажем следующее свойствоamn·m=an. Для этого необходимо показать, что an – число, положительное или равное нулю. При возведении в степень n·m равно am. Если число a является положительным или равным нулю, то n-ой степени из числа a является числом положительным или равным нулю При этом an·mn=annm, что и требовалось доказать.

Для того, чтобы закрепить полученные знания, рассмотрим несколько примеров

2312=24.

Докажем следующее свойство – свойство корня из степени вида amn=anm. Очевидно, что при a≥0 степень anm является неотрицательным числом. Более того, ее n-ая степень равна am, действительно, anmn=anm·n=annm=am. Этим и доказано рассматриваемое свойство степени.

Например, 2353=2335.

Необходимо доказательство, что для любых положительных чисел a и b выполнено условие a<b. Рассмотрим неравенство an<bn. Воспользуемся методом от противного an≥bn. Тогда, согласно свойству, о котором говорилось выше, неравенство считается верным ann≥bnn, то есть, a≥b. Но это не соответствует условию a<b. Следовательно, an<bn при a<b.

Для примера приведем 124<15234.

Рассмотрим свойство корня n-ой степени. Необходимо для начала рассмотреть первую часть неравенства. При m>n и 0<a<1справедливо am>an. Предположим, что am≤an. Свойства позволят упростить выражение до anm·n≤amm·n. Тогда, согласно свойствам степени с натуральным показателем, выполняется неравенство anm·nm·n≤amm·nm·n, то есть, an≤am. Полученное значение при m>n и 0<a<1 не соответствует свойствам, приведенным выше.

Таким же способом можно доказать, что при m>n и a>1справедливо условие am<an.

Для того, чтобы закрепить приведенные свойства, рассмотрим несколько конкретных примеров. Рассмотрим неравенства, используя конкретные числа.

Пример 6

0,73>0,75 и 12>127.

Источник

Зачем нужен квадратный корень? Очень хороший вопрос…

Попробуй на калькуляторе извлечь корень из ( displaystyle 3).

Получается число, которое никогда не кончается: ( sqrt{3}=1,732050807568ldots )

Как же такое число запомнить? А как его записать, если, допустим, нельзя округлять? Например на ЕГЭ?

Очень просто. С помощью квадратного корня. Пишешь ( sqrt{3} ) и все.

Именно для упрощения записи таких чисел и было введено понятие квадратного корня. К слову такие числа называются иррациональными.

Ну и давай теперь разберемся с квадратным корнем…

К примеру, перед нами уравнение ( {{x}^{2}}=4 ).

Какое решение у данного уравнения? Какие числа можно возвести в квадрат и получить при этом ( 4 )?

Вспомнив таблицу умножения, ты легко дашь ответ, что есть два таких числа: ( 2 ) и ( -2 ).

Квадратный корень – это решение такого уравнения!

Дадим первое определение квадратного корня:

Квадратный корень из числа ( a ) — это решение уравнения ( {{x}^{2}}=a ).

Операция вычисления значения корня из числа ( a ) называется «извлечением квадратного корня» из этого числа.

У квадратного корня есть специальный символ: ( sqrt{ } ), который называется радикалом.

Но есть еще одно равнозначное определение квадратного корня. Сейчас мы его тоже приведем.

Что такое арифметический квадратный корень?

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа (a) называется такое неотрицательное число, квадрат которого равен (a). ( (sqrt{a}=x, {{x}^{2}}=a; x, age 0)).

А почему же число ( a) (число под корнем) должно быть обязательно неотрицательным?

Например, чему равен ( sqrt{-9})?

Так-так, попробуем подобрать. Может, три?

Проверим: ( {{3}^{2}}=9), а не ( -9).

Может, ( left( -3 right))?

Опять же, проверяем: ( {{left( -3 right)}^{2}}=9).

Ну что же, не подбирается?

Это и следовало ожидать – потому что нет таких чисел, которые при возведении в квадрат дают отрицательное число! Это надо запомнить!

Число или выражение под знаком корня должно быть неотрицательным!

Однако ты наверняка уже заметил, что не только число под корнем должно быть неотрицательным, но и само значение тоже должно быть неотрицательным!

Ведь в определении сказано, что «квадратным корнем из числа ( a) называется такое неотрицательное число, квадрат которого равен ( a)».

Но подождите! В самом начале мы разбирали пример ( {{x}^{2}}=4) и один из ответов был отрицательным числом!

Мы подбирали числа, которые можно возвести в квадрат и получить при этом ( displaystyle 4). Ответом были ( displaystyle 2) и ( displaystyle -2)

А тут говорится, что квадратным корнем должно быть «неотрицательное число»! Почему?

Такой вопрос вполне уместен. Здесь необходимо просто разграничить понятия квадратного уравнения и арифметического квадратного корня.

К примеру, ( displaystyle {{x}^{2}}=4) (квадратное уравнение) не равносильно выражению ( x=sqrt{4}) (арифмитический квадратный корень).

Из ( {{x}^{2}}=4) следует, что

( left| x right|=sqrt{4}), то есть ( x=pm sqrt{4}=pm 2) или ( {{x}_{1}}=2); ( {{x}_{2}}=-2)

(не помнишь почему так? Почитай тему “Модуль числа”!)

А из ( x=sqrt{4}) следует, что ( x=2).

Конечно, это очень путает, но это необходимо запомнить, что знаки “плюс-минус” являются результатом решения квадратного уравнения, так как при решении уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат.

В наше квадратное уравнение подходит как ( 2), так и ( x=-2).

Однако, если просто извлекать квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

Наглядный пример разницы между квадратным уравнением и квадратным корнем

Этот наглядный пример привёл наш читатель Игорь, спасибо ему за это:

Пусть есть две ситуации:

1) ( x^2=64;)

2) ( x= sqrt{64}.)

В первом случае у нас квадратное уравнение и его решением будет ( |х| =sqrt{64}) (уже видно отличие от второго случая) и далее получаем два корня ( x_1 = +8text{ и }х_2 = -8.)

Во втором случае у нас нет квадратного уравнения, просто х равен корню из числа и в этом случае ответ всегда “одно неотрицательное число”, то есть 8.

Запись иррациональных чисел с помощью квадратного корня

А теперь попробуй решить такое уравнение ( {{x}^{2}}=3).

Уже все не так просто и гладко, правда? Попробуй перебрать числа, может, что-то и выгорит?

Начнем с самого начала – с нуля: ( {{0}^{2}}=0) – не подходит.

Двигаемся дальше ( displaystyle x=1); ( displaystyle {{1}^{2}}=1) – меньше трех, тоже отметаем.

А что если ( displaystyle x=2)?

Проверим: ( displaystyle {{2}^{2}}=4) – тоже не подходит, т.к. это больше трех.

С отрицательными числами получится такая же история.

И что же теперь делать? Неужели перебор нам ничего не дал?

Совсем нет, теперь мы точно знаем, что ответом будет некоторое число между ( displaystyle 1) и ( displaystyle 2), а также между ( displaystyle -2) и ( displaystyle -1).

Кроме того, очевидно, что решения не будут целыми числами. Более того, они не являются рациональными.

И что дальше?

Давай построим график функции ( displaystyle y={{x}^{2}}) и отметим на нем решения.

График квадратичной функции

Попробуем обмануть систему и получить ответ с помощью калькулятора (как мы это делали в начале)!

Извлечем корень из ( displaystyle 3), делов-то!

Ой-ой-ой, выходит, что ( sqrt{3}=1,732050807568ldots ) Такое число никогда не кончается.

Как же такое запомнить, ведь на экзамене калькулятора не будет!?

Все очень просто, это и не надо запоминать, необходимо помнить (или уметь быстро прикинуть) приблизительное значение. ( sqrt{3}) и ( -sqrt{3}) уже сами по себе ответы.

Такие числа называются иррациональными, именно для упрощения записи таких чисел и было введено понятие квадратного корня.

Еще один пример для закрепления

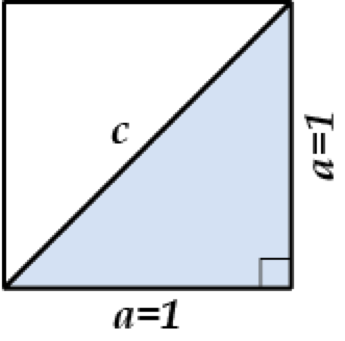
Разберем такую задачку: тебе необходимо пересечь по диагонали квадратное поле со стороной ( displaystyle 1) км, сколько км тебе предстоит пройти?

Квадрат

Самое очевидное здесь рассмотреть отдельно треугольник и воспользоваться теоремой Пифагора: ( {{c}^{2}}={{a}^{2}}+{{a}^{2}}).

Таким образом, ( {{c}^{2}}=1+1=2).

Так чему же здесь равно искомое расстояние?

Очевидно, что расстояние не может быть отрицательным, получаем, что ( c=sqrt{2}). Корень из двух приблизительно равен ( displaystyle 1,41), но, как мы заметили раньше, ( c=sqrt{2}) – уже является полноценным ответом.

Извлечение корней

Чтобы решение примеров с корнями не вызывало проблем, необходимо их видеть и узнавать.

Для этого необходимо знать, по меньшей мере, квадраты чисел от ( displaystyle 1) до ( displaystyle 20), а также уметь их распознавать.

То есть, тебе необходимо знать, что ( displaystyle 15) в квадрате равно ( displaystyle 225), а также, наоборот, что ( displaystyle 225) – это ( displaystyle 15) в квадрате.

Первое время в извлечении корня тебе поможет эта таблица.

Таблица квадратов

Как только ты прорешаешь достаточное количество примеров, то надобность в ней автоматически отпадет.

Попробуй самостоятельно извлечь квадратный корень в следующих выражениях:

1
( sqrt{0}=?);
2
( sqrt{64}=?);
3
( sqrt{121}=?);
4
( sqrt{289}=?);

Ответы:

1
( displaystyle 0);
2
( displaystyle 8);
3
( displaystyle 11);
4
( displaystyle 17);

Ну как, получилось? Теперь давай посмотрим такие примеры:

1
( sqrt{0,0196}=?);
2
( sqrt{0,0961}=?);
3
( sqrt{0,0144}=?).

Ответы:

1
( displaystyle 0,14);
2
( displaystyle 0,31);
3
( displaystyle 0,12);

Свойства арифметического квадратного корня

Теперь ты знаешь, как извлекать корни и пришло время узнать о свойствах арифметического квадратного корня. Их всего 3:

умножение;
деление;
возведение в степень.

Их ну просто очень легко запомнить с помощью этой таблицы и, конечно же, тренировки:

СВОЙСТВО	ПРИМЕР
Корень произведения равен произведению корней: ( displaystyle sqrt[{}]{ab}=sqrt[{}]{a}cdot sqrt[{}]{b})	( displaystyle sqrt[{}]{64cdot 9}=sqrt[{}]{64}cdot sqrt[{}]{9}=8cdot 3=24)
Корень из дроби – это корень из числителя и корень из знаменателя: ( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b > 0)	( displaystyle sqrt[{}]{frac{64}{9}}=frac{sqrt[{}]{64}}{sqrt[{}]{9}}=frac{8}{3}=2frac{2}{3})
Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение: ( displaystyle {{left( sqrt{a} right)}^{n}}={{left( sqrt{{{a}^{n}}} right)}^{{}}}), при ( displaystyle age 0)	( displaystyle {{left( sqrt{2} right)}^{4}}=sqrt{{{2}^{4}}}=sqrt{16}=4)

Попробуем решить по несколько примеров на каждое свойство!

Умножение корней

Взглянул еще раз на табличку… И, поехали!

Начнем с простенького:

1
( sqrt{5}cdot sqrt{3}=sqrt{15})
2
( sqrt{2}cdot sqrt{6}=sqrt{12})

Минуууточку. ( 12) это ( displaystyle 4cdot 3), а это значит, что мы можем записать вот так:

( sqrt{2}cdot sqrt{6}=sqrt{12}=sqrt{4cdot 3}=sqrt{4}cdot sqrt{3}=2sqrt{3})

Усвоил? Вот тебе следующий:

( displaystyle sqrt{4}cdot sqrt{6}=2cdot sqrt{6}=2sqrt{6})

Корни из получившихся чисел ровно не извлекаются? Не беда – вот тебе такие примеры:

( displaystyle sqrt{2}cdot sqrt{8}=sqrt{16}=4)

( displaystyle sqrt{12}cdot sqrt{3}=sqrt{36}=6)

А что, если множителей не два, а больше? То же самое! Формула умножения корней работает с любым количеством множителей:

( displaystyle sqrt{5}cdot sqrt{3}cdot sqrt{2}=sqrt{10cdot 3}=sqrt30)

Теперь полностью самостоятельно:

1
( displaystyle sqrt{4}cdot sqrt{6}cdot sqrt{5})
2
( displaystyle sqrt{3}cdot sqrt{6}cdot sqrt{7})
3
( displaystyle sqrt{32}cdot sqrt{2})

Ответы:

1
( displaystyle sqrt{4}cdot sqrt{6}cdot sqrt{5}=sqrt{4cdot 6cdot 5}=sqrt{120}=sqrt{4cdot 30}=2sqrt{30});
2
( displaystyle sqrt{3}cdot sqrt{6}cdot sqrt{7}=sqrt{3cdot 6cdot 7}=sqrt{126});
3
( displaystyle sqrt{32}cdot sqrt{2}=sqrt{32cdot 2}=sqrt{64}=8).

Молодец! Согласись, все очень легко, главное знать таблицу умножения!

С умножением корней разобрались, теперь приступим к свойству деления.

Напомню, что формула в общем виде выглядит так:

( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b>0).

А значит это, чтокорень из частного равен частному корней.

Ну что, давай разбираться на примерах:

( displaystyle frac{sqrt{12}}{sqrt{3}}=sqrt{frac{12}{3}}=sqrt{4}=2)

Вот и вся наука. А вот такой пример:

( displaystyle frac{sqrt{12}}{3}=frac{sqrt{12}}{sqrt{9}}=sqrt{frac{12}{9}}=sqrt{frac{4}{3}}=frac{2}{sqrt{3}})

Все не так гладко, как в первом примере, но, как видишь, ничего сложного нет.

А что, если попадется такое выражение:

( displaystyle sqrt{frac{144}{225}}=?)

Надо просто применить формулу в обратном направлении:

( displaystyle sqrt{frac{144}{225}}=frac{sqrt{144}}{sqrt{225}}=frac{12}{15}=frac{4}{5}=0,8)

А вот такой примерчик:

( displaystyle sqrt{0,16}=sqrt{frac{16}{100}}=frac{4}{10}=0,4)

Еще ты можешь встретить такое выражение:

( displaystyle sqrt{5frac{19}{25}}=?)

Все то же самое, только здесь надо вспомнить, как переводить дроби (если не помнишь, загляни в тему дроби и возвращайся!). Вспомнил? Теперь решаем!

( displaystyle sqrt{5frac{19}{25}}=sqrt{frac{144}{25}}=frac{12}{5}=2,4)

Уверена, что ты со всем, всем справился, теперь попробуем возводить корни в степени.

А что же будет, если квадратный корень возвести в квадрат? Все просто, вспомним смысл квадратного корня из числа ( displaystyle a) – это число, квадратный корень которого равен ( displaystyle a).

Так вот, если мы возводим число, квадратный корень которого равен ( displaystyle a), в квадрат, то что получаем?

Ну, конечно, ( displaystyle a)!

Рассмотрим на примерах:

( displaystyle {{left( sqrt{12} right)}^{2}}=12)

( displaystyle {{left( sqrt{17} right)}^{2}}=17)

Все просто, правда? А если корень будет в другой степени? Ничего страшного!

Придерживайся той же логики и помни свойства и возможные действия со степенями.

Забыл?

Почитай теорию по теме «Степень и ее свойства» и тебе все станет предельно ясно.

Вот, к примеру, такое выражение:

( displaystyle {{left( sqrt{5} right)}^{6}}={{left( {{left( sqrt{5} right)}^{2}} right)}^{3}}={{5}^{3}}=125)

В этом примере степень четная, а если она будет нечетная? Опять же, примени свойства степени и разложи все на множители:

( displaystyle {{left( sqrt{5} right)}^{7}}={{left( sqrt{5} right)}^{6}}cdot sqrt{5}=125sqrt{5})

С этим вроде все ясно, а как извлечь корень из числа в степени? Вот, к примеру, такое:

( displaystyle sqrt{{{3}^{2}}}=sqrt{9}=3)

Довольно просто, правда? А если степень больше двух? Следуем той же логике, используя свойства степеней:

( displaystyle sqrt{{{3}^{6}}}=sqrt{{{left( {{3}^{3}} right)}^{2}}}={{3}^{3}}=27)

( displaystyle sqrt{{{3}^{5}}}=sqrt{{{3}^{4}}cdot 3}=sqrt{{{left( {{3}^{2}} right)}^{2}}cdot 3}={{3}^{2}}cdot sqrt{3}=9sqrt{3})

Ну как, все понятно? Тогда реши самостоятельно примеры:

1
( displaystyle sqrt{{{left( -3 right)}^{2}}})
2
( displaystyle sqrt{{{6}^{6}}})
3
( displaystyle {{left( sqrt{8} right)}^{7}})

А вот и ответы:

1
( displaystyle sqrt{{{left( -3 right)}^{2}}}=sqrt{9}=3)
2
( displaystyle sqrt{{{6}^{6}}}=sqrt{{{left( {{6}^{3}} right)}^{2}}}={{6}^{3}}=216)
3
( displaystyle {{left( sqrt{8} right)}^{7}}={{left( sqrt{8} right)}^{6}}cdot sqrt{8}=512sqrt{8})

Что мы только не научились делать с корнями! Осталось только потренироваться вносить число под знак корня!

Это совсем легко!

( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8}=sqrt{16cdot 6}-sqrt{4cdot 3cdot 8}=sqrt{96}-sqrt{96}=0)

Допустим, у нас записано число ( displaystyle 3sqrt{5})

Что мы можем с ним сделать? Ну конечно, спрятать тройку под корнем, помня при этом, что тройка – корень квадратный из ( displaystyle 9)!

( displaystyle 3sqrt{5}=sqrt{9}cdot sqrt{5}=sqrt{45})

Зачем нам это нужно? Да просто, чтобы расширить наши возможности при решении примеров:

( displaystyle 3sqrt{10}-sqrt{45}cdot sqrt{2}=sqrt{90}-sqrt{90}=0)

Как тебе такое свойство корней? Существенно упрощает жизнь? По мне, так точно! Только надо помнить, что вносить под знак квадратного корня мы можем только положительные числа.

Реши самостоятельно вот этот пример – ( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8})
Справился? Давай смотреть, что у тебя должно получиться:

( displaystyle 4sqrt{6}-2sqrt{3}cdot sqrt{8}=sqrt{16cdot 6}-sqrt{4cdot 3cdot 8}=sqrt{96}-sqrt{96}=0)

Молодец! У тебя получилось внести число под знак корня! Перейдем к не менее важному – рассмотрим, как сравнивать числа, содержащие квадратный корень!

Зачем нам учиться сравнивать числа, содержащие квадратный корень?

Очень просто. Часто, в больших и длиииинных выражениях, встречающихся на экзамене, мы получаем иррациональный ответ (помнишь, что это такое? Мы с тобой сегодня об этом уже говорили!)

Полученные ответы нам необходимо расположить на координатной прямой, например, чтобы определить, какой интервал подходит для решения уравнения. И вот здесь возникает загвоздка: калькулятора на экзамене нет, а без него как представить какое число больше, а какое меньше? То-то и оно!

Например, определи, что больше: ( displaystyle 3sqrt{7}) или ( displaystyle 2sqrt{17})?

Сходу и не скажешь. Ну что, воспользуемся разобранным свойством внесения числа под знак корня?

Тогда вперед:

( displaystyle 3sqrt{7}=sqrt{9cdot 7}=sqrt{63})

( displaystyle 2sqrt{17}=sqrt{4cdot 17}=sqrt{68})

Ну и, очевидно, что чем больше число под знаком корня, тем больше сам корень!

Т.е. если ( displaystyle 68>63), значит, ( displaystyle sqrt{68}>sqrt{63}).

Отсюда твердо делаем вывод, что ( displaystyle 3sqrt{7}<2sqrt{17}). И никто не убедит нас в обратном!

До этого мы вносили множитель под знак корня, а как его вынести? Надо просто разложить его на множители и извлечь то, что извлекается!

( displaystyle sqrt{98}=sqrt{49cdot 2}=sqrt{49}cdot sqrt{2}=7sqrt{2})

Можно было пойти по иному пути и разложить на другие множители:

( displaystyle sqrt{98}=sqrt{7cdot 14})

Что дальше? А дальше раскладываем на множители до самого конца:

( displaystyle sqrt{98}=sqrt{7cdot 14}=sqrt{7cdot 7cdot 2}=sqrt{{{7}^{2}}cdot 2}=7sqrt{2})

Неплохо, да? Любой из этих подходов верен, решай как тебе удобно.

Разложение на множители очень пригодится при решении таких нестандартных заданий, как вот это:

( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12})

Не пугаемся, а действуем! Разложим каждый множитель под корнем на отдельные множители:

А теперь попробуй самостоятельно (без калькулятора! его на экзамене не будет):

( displaystyle sqrt{15}cdot sqrt{180}cdot sqrt{12}=sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6})

Разве это конец? Не останавливаемся на полпути!

( displaystyle begin{array}{l}sqrt{5cdot 3}cdot sqrt{36cdot 5}cdot sqrt{2cdot 6}=sqrt{5cdot 3}cdot sqrt{3cdot 12cdot 5}cdot sqrt{2cdot 3cdot 2}=\=sqrt{5cdot 3}cdot sqrt{3cdot 2cdot 2cdot 3cdot 5}cdot sqrt{2cdot 3cdot 2}end{array})

На простые множители разложили. Что дальше? А дальше пользуемся свойством умножение корней и записываем все под одним знаком корня:

( displaystyle begin{array}{l}sqrt{5cdot 3cdot 3cdot 2cdot 2cdot 3cdot 5cdot 2cdot 3cdot 2}=sqrt{5cdot 5cdot 3cdot 3cdot 3cdot 3cdot 2cdot 2cdot 2cdot 2}=\=sqrt{25}cdot sqrt{81}cdot sqrt{16}=5cdot 9cdot 4=180end{array})

Вот и все, не так все и страшно, правда?

( displaystyle sqrt{15}cdot sqrt{54}cdot sqrt{10}=?)

Получилось ( displaystyle 90)? Молодец, все верно!

А теперь попробуй вот такой пример решить:

( displaystyle sqrt{4225}=?)

А пример-то – крепкий орешек, так сходу и не разберешься, как к нему подступиться. Но нам он, конечно, по зубам.

Ну что, начнем раскладывать ( displaystyle 4225) на множители? Сразу заметим, что можно поделить число на ( displaystyle 5) (вспоминаем признаки делимости):

( displaystyle begin{array}{l}sqrt{4225}=sqrt{845cdot 5}=sqrt{169cdot 5cdot 5}=\=sqrt{13cdot 13cdot 5cdot 5}=5cdot 13=65end{array})

А теперь, попробуй сам (опять же, без калькулятора!):

( displaystyle sqrt{2304}=?)

Ну что, получилось ( displaystyle 48)? Молодец, все верно!

Определение

Квадратным корнем (арифметическим квадратным корнем) из неотрицательного числа ( displaystyle a) называется такое неотрицательное число, квадрат которого равен ( displaystyle a).

Главное!

Если мы просто извлекаем квадратный корень из чего-либо, то всегда получаем один неотрицательный результат.

Свойства арифметического корня

СВОЙСТВО	ПРИМЕР
Корень произведения равен произведению корней: ( displaystyle sqrt[{}]{ab}=sqrt[{}]{a}cdot sqrt[{}]{b})	( displaystyle sqrt[{}]{64cdot 9}=sqrt[{}]{64}cdot sqrt[{}]{9}=8cdot 3=24)
Корень из дроби – это корень из числителя и корень из знаменателя: ( displaystyle sqrt[{}]{frac{a}{b}}=frac{sqrt[{}]{a}}{sqrt[{}]{b}}), если ( displaystyle age 0 , b > 0)	( displaystyle sqrt[{}]{frac{64}{9}}=frac{sqrt[{}]{64}}{sqrt[{}]{9}}=frac{8}{3}=2frac{2}{3})
Чтобы возвести корень в степень, достаточно возвести в эту степень подкоренное значение: ( displaystyle {{left( sqrt{a} right)}^{n}}={{left( sqrt{{{a}^{n}}} right)}^{{}}}), при ( displaystyle age 0)	( displaystyle {{left( sqrt{2} right)}^{4}}=sqrt{{{2}^{4}}}=sqrt{16}=4)

Сравнение корней

При сравнении квадратных корней необходимо помнить, что чем больше число под знаком корня, тем больше сам корень.

P.S. Последний бесценный совет ????

Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.

Почему?

Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!

Теперь самое главное.

Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.

Проблема в том, что этого может не хватить…

Для чего?

Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.

Я не буду тебя ни в чем убеждать, просто скажу одну вещь…

Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.

Но и это не главное.

Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…

Но думай сам…

Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?

Набить руку, решая задачи.

На экзамене у тебя не будут спрашивать теорию.

Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.

Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!

Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.

Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.

А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.

После регистрации ты сможешь:

проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
подтянуть слабые места с помощью видеоуроков, вебинаров;
понять тему с помощью статей учебника YouClever;
набить руку, решая задачи и получая проверку и решения;
сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.

Бонус: информатика и физика.

И в заключение…

Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.

“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.

Найди задачи и решай!

Мы постарались объяснить тебе без воды все что нужно знать на экзамене про квадратный корень.

Теперь твоя очередь. Напиши нам сложная это для тебя тема или нет.

Узнал ты что-то новое или все было и так ясно.

Задай вопросы, если есть. Мы обязательно ответим.

Пиши в комментариях и удачи на экзаменах!

Источник