Какие свойства алгоритма нарушены

Цели урока:
- познакомить с понятием алгоритма, исполнителем
алгоритма, видами исполнителя, средой, СКИ и
системой отказов исполнителя, свойствами
алгоритма, показать среду, СКИ и систему отказов
для конкретного исполнителя, - развивать умение работать самостоятельно,
творчески. - воспитывать нравственное отношение к труду.
ХОД УРОКА
Презентация 1
В течение всей жизни каждый человек постоянно
пользуется набором всевозможных алгоритмов —
правил, которые заложены природой, даны
воспитанием, обучением, тренировкой, выработаны
на основе собственного опыта. Инструкции, в
которых указано, как пользоваться лифтом,
телефоном, различными автоматами и бытовыми
приборами, правила перехода улицы, оказания
первой медицинской помощи, распорядок дня,
кулинарные рецепты, порядок проведения
химического опыта, правила вычислений, методы
решения алгебраических и геометрических задач —
все это можно считать алгоритмами. Таким образом,
все мы живем в мире алгоритмов. Алгоритмы
экономят силы и время человека, так как однажды
усвоенным правилом (алгоритмом) он может
пользоваться всю жизнь.
Приведите пример алгоритма перехода дороги с
светофором, и без светофора.
Ваш мозг постоянно занят работой, поиском
решений. Говорят, что человек составляет
алгоритм.
Тема нашего сегодняшнего урока. Алгоритм.
Свойства алгоритма.
Учащиеся записывают тему урока (с
презентации).
На экране вы видите команды, необходимо
составить алгоритм заваривания чая.
Работа идет со всем классом, учащиеся
обсуждают о выборе последовательности команд,
учитель на доске регистрирует их ответ.
- размешать сахар ложечкой;
- добавить кипятку;
- налить в чашку заварку;
- вскипятить воду;
- положить сахар.
У вас должен был получиться такой алгоритм:
- вскипятить воду;
- налить в чашку заварку;
- добавить кипятку;
- положить сахар;
- размешать сахар ложечкой;
В природе все взаимосвязано, все на все влияет и
все зависит друг от друга. Складываются сложные
цепочки событий. Если вынуть хоть одно звено, вся
цепочка разорвется.
Как вы думаете, что будет если убрать из рецепта
вторую команду? А четвертую?
Надо научится выстраивать в нужном порядке все
звенья какой-нибудь жизненной или
математической задачи. Эти умения нужны и при
обработке информации. Информацию следует
обрабатывать по определенным правилам, которые
выполняются в определенном порядке.
Итак, давайте с вами, попробуем дать
определения понятию алгоритм.
Учащиеся формулируют и записывают с доски.
Алгоритм – понятное и точное
предписание исполнителю совершить
последовательность действий, направленных на
достижение указанной цели или на решение
поставленной задачи.
Учащиеся записывают в тетрадь определение.
Синонимы слова «алгоритм»:
- план;
- инструкция;
- рецепт;
- предписание.
Происхождение термина «алгоритм» связывают с
именем великого узбекского математика и
астронома аль-Хорезми (жившего в IX в.). Абу
Абдуллах Мухаммад ибн Муса аль-Хорезми (ок. 783,
Хива , Хорезм — ок. 850, Багдад) — один из
крупнейших средневековых ученых (математик,
астроном, географ и историк) IX века, основатель
классической алгебры.
Ал-Хорезми известен прежде всего своей «Книгой о
восполнении и противопоставлении» («Аль-китаб
аль-мухтасар фи хисаб аль-джабр ва-ль-мукабала»),
которая сыграла важнейшую роль в истории
математики. От названия этой книги произошло
слово «алгебра».
В своих трудах по арифметике и алгебре он
разработал, в частности, правила выполнения
четырех арифметических операций над
многозначными десятичными числами. Эти правила
определяют последовательность действий, которые
необходимо выполнить, чтобы получить сумму
чисел, произведение и т. д. Почти в таком же виде
эти правила изучаются всеми школьниками в
начальных классах.
Латинский перевод книги начинается словами
«Dixit Algorizmi» (сказал Алгоризми). Так как сочинение
об арифметике было очень популярно в Европе, имя
автора (Algorizmi или Algorizmus) стало нарицательным и
средневековые математики так называли
арифметику, основанную на десятичной
позиционной системе счисления. Позднее
европейские математики стали называть так
всякую систему вычислений по определенному
правилу. В настоящее время термин «алгоритм»
означает набор инструкций, описывающих порядок
действий исполнителя для достижения результата
решения задачи за конечное число действий.
Затем понятие алгоритма переместилось в
область логики, где появилась теория алгоритмов,
изучавшая процесс доказательств или
разрешимость и неразрешимость математических
задач. В 1937 году, когда английский
математик Алан Тьюринг доказал
теоретически возможность построения устройства,
осуществляющего алгоритм. Такое абстрактное
устройство получило название МАШИНА ТЬЮРИНГА.
Аналогичный, но более простой исполнитель
алгоритма – МАШИНА ПОСТА. Когда же были
созданы первые ЭВМ, понятие алгоритма и теория
алгоритмов переместились в новую науку,
связанную с этими вычислительными устройствами
– информатику.
Приведите примеры алгоритмов.
А теперь скажите кто может выполнить данный
алгоритм?
Приведите пример алгоритмов с разными
исполнителями.
Получается, всякий алгоритм составляется в
расчете на определенного исполнителя. Им может
быть человек, робот, компьютер и др. Чтобы
составить алгоритм для исполнителя, нужно знать,
какие команды исполнитель может понять и
исполнить, а какие нет.
Исполнитель – объект, который будет выполнять
алгоритм.
Приведите примеры исполнителей и что они
могут делать.
В классе исполнителей выделяют два типа:
формальные, неформальные. Формальный
исполнитель одну и ту же команду всегда выполнит
одинаково, неформальный может выполнять команду
по-разному. Неформальный исполнитель – человек,
формальный – технические устройства.
У каждого исполнителя можно выделить: среду
исполнителя, систему команд исполнителя, систему
отказов.
Среда – обстановка, в которой
работает исполнитель.
Система команд исполнителя (СКИ) –
совокупность команд, которую исполнитель умеет
выполнять.
Система отказов – ситуации сбоя
работы исполнителя, которые возникают, если
команда вызывается пpи недопустимом для нее
состоянии сpеды («не понимаю», «не могу»).
«Не понимаю» – возникает тогда, когда
исполнителю дается команда не входящая в его СКИ,
«не могу» – когда команда из СКИ не может быть
выполнена в конкретных условиях среды.
Укажите для данных примеров среду, ски,
систему отказов.
Свойства алгоритмов
1. Как мы уже знаем, алгоритм задает полную
последовательность действий, которые необходимо
выполнять для решения задачи. При этом, как
правило, для выполнения этих действий их
расчленяют (разбивают) в определенной
последовательности на простые шаги. Возникает
упорядоченная запись совокупности четко
разделенных предписаний (директив, команд),
образующих прерывную (или, как говорят,
дискретную) структуру алгоритма. Выполнить
действия следующего предписания можно лишь
выполнив действия предыдущего.
Под ДИСКРЕТНОСТЬЮ понимают возможность
разбиения алгоритма на отдельные элементарные
действия, выполнение которых человеком или
машиной не вызывает сомнения.
Пример по алгоритму заваривая чая
2. Чтобы исполнитель сумел решить поставленную
перед ним задачу, используя алгоритм, он должен
уметь выполнить каждое его указание. Иными
словами, он должен понимать суть управления. То
есть при составлении алгоритма нужно
обязательно учитывать “правила игры”, т.е.
систему предписаний (или систему команд), которые
понимает ЭВМ. Мы будем говорить в данном случае о
“понятности” алгоритма.
Под “ПОНЯТНОСТЬЮ” алгоритмов понимают
указания, которые понятны исполнителю.
Пример по пришиванию пуговицы.
3. Будучи понятным, алгоритм не должен все же
содержать предписаний, смысл которых может
восприниматься неоднозначно. Этими свойствами
часто не обладают предписания и инструкции,
которые составляются для людей.
Например, вспомним известную всем притчу о
царской воле. Царь приказал подчиненным
выполнить такой указ: “Казнить нельзя
помиловать”. Он забыл в указе поставить
запятую, а подчиненные не знали, что им делать.
Указание “казнить нельзя, помиловать” и
“казнить, нельзя помиловать” задают совсем
разные действия, от которых зависит жизнь
человека.
Кроме того, в алгоритмах недопустимы такие
ситуации, когда после выполнения очередного
предписания алгоритма исполнителю неясно, какое
из них должно выполняться на следующем шаге.
Под ОДНОЗНАЧНОСТЬЮ алгоритмов понимается
единственность толкования правил выполнения
действий и порядка их выполнения.
Пример, фрагмент мультфильма «Стран
невыученных уроков».
4. Очень важно, чтобы составленный алгоритм
обеспечивал решение не одной частной задачи, а
мог выполнять решение широкого класса задач
данного типа.
Алгоритм можно использовать для любого
квадратного у равнения. Такой алгоритм будет
МАССОВЫЙ.
Пример с чайниками, обогревателями.
5. Под КОНЕЧНОСТЬЮ алгоритмов понимают
завершение работы алгоритма в целом за конечное
число шагов.
Пример с ловлей рыбы.
6. Еще к желательным свойствам алгоритмов нужно
отнести РЕЗУЛЬТАТИВНОСТЬ, она предполагает, что
выполнение алгоритмов должно завершаться
получением определенных результатов.
Подобные ситуации в информатике возникают, когда
какие-либо действия невозможно выполнить. В
математике такие ситуации называют
неопределенностью. Например, деление числа на
ноль, извлечение квадратного корня из
отрицательного числа, да и само понятие
бесконечности неопределенно. Поэтому, если
алгоритм задает бесконечную последовательность
действий, то в этом случае он также считается
результатом неопределенным.
Но можно действовать по-другому. А именно:
указать причину неопределенного результата. В
таком случае, пояснения типа “на ноль делить
нельзя”, “компьютер выполнить такое не в
состоянии” и т.п. можно считать результатом
выполнение алгоритма.
Таким образом, свойство результативности
состоит в том, что во всех” случаях можно
указать, что мы понимаем под результатом
выполнения алгоритма.
Пример с нахождением стрелы Ивана Царевича у
лягушки.
7. И последнее общее свойство алгоритмов – их
правильность.
Мы говорим, что алгоритм ПРАВИЛЬНЫЙ, если его
выполнение дает правильные результаты решения
поставленных задач.
Соответственно мы говорим, что алгоритм СОДЕРЖИТ
ОШИБКИ, если можно указать такие допустимые
исходные данные или условия, при которых
выполнение алгоритма либо не завершится вообще,
либо не будет получено никаких результатов, либо
полученные результаты окажутся неправильными.
Пример с арифметическим выражением.
Вывод:
Основные свойства алгоритмов:
- дискретность;
- понятность;
- однозначность;
- массовость;
- результативность;
- конечность;
- правильность.
Учащиеся записывают в тетрадь свойства.
Решение задач на определение свойств.
Обсуждение свойств с классом.
Задание 1.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция по варке манной каши
Молоко вскипятить добавить соль, сахар, засыпать
тонкой струйкой, непрерывно помешивая манную
крупу, довести до кипения, прокипятить минут 5-7,
добавить масло и дать остыть.
Нет понятности: какое количество (в граммах)
брать продуктов.
Возможный исправленный вариант
- Включить плиту
- Влить в кастрюлю 1,5 литра молока
- Добавить 5 грамм соли, 15 грамм сахара
- Довести молоко до кипения
- 8 столовых ложек манной крупы засыпать тонкой
струйкой, непрерывно помешивая молоко - Довести до кипения
- Кипятить 5 минут
- Добавить 20 грамм сливочного масла
- Выключить плиту, снять с плиты кастрюлю.
Задание 2.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция нахождения большего из двух данных
чисел.
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше
Нет результативности. Что делать в том случае,
если А=В?
Возможный исправленный вариант
- Из числа А вычесть число В.
- Если получилось отрицательное значение, то
сообщить, что число В больше. - Если получилось положительное значение, то
сообщить, что число А больше - Если получился ноль, сообщить, что числа равны
Задание 3.
Определить какое свойство алгоритма, не
выполняется в данной инструкции и какие
изменения необходимо внести, чтобы получился
алгоритм.
Инструкция покраски забора
- Покрасить первую доску.
- Переместиться к следующей доске.
- Перейти к действию 1.
Нет конечности. Что делать в том случае, когда
доски закончились?
Возможный исправленный вариант
- Покрасить первую доску.
- Если есть еще доска, переместиться к следующей
доске. - Перейти к действию 1.
- Если доски закончились, завершить работу.
Практическая работа в парах (5 мин.)
Приложение 1
Задание 1. Исправьте алгоритм
«Получения кипятка», чтобы предотвратить
несчастный случай.
Задание 2. Используя представленные
команды, составить алгоритм покраски мяча
Задание 3. Составить инструкцию, в
которой не выполняется хотя бы одно свойство
алгоритма. Записать какие изменения нужно в нее
внести, чтобы получить алгоритм.
Тест самопроверкой (5 мин.)
1. Алгоритм – это:
А) Указание на выполнение действий,
Б) Система правил, описывающая
последовательность действий, которые необходимо
выполнить для решения задачи,
В) Процесс выполнения вычислений, приводящих к
решению задачи
2. Свойство алгоритма – дискретность, выражает,
что:
А) Команды должны следовать последовательно
друг за другом,
Б) Каждая команда должна быть описана в расчете
на конкретного исполнителя,
В) Разбиение алгоритма на конечное число команд
3. Среда исполнителя – это:
А) Обстановка, в которой работает исполнитель.
Б) Объект, который будет выполнять алгоритм
В) Совокупность команд, которую исполнитель
умеет выполнять.
4. В расчете на кого должен строиться алгоритм:
А) В расчете на ЭВМ,
Б) В расчете на умственные способности товарища,
В) В расчете на конкретного исполнителя
5. Какое из перечисленных свойств относится к
свойствам алгоритма:
А) Визуальность,
Б) Совокупность,
В) Понятность
6. Исполнитель «человек» – это
А) Формальный исполнитель
Б) Неформальный исполнитель
В) Нормальный исполнитель
Проверка теста.
Подведение итогов (5 мин.)
Домашнее задание:
1. Выучить теоретический материал
2. Привести 3 примера алгоритмов для различных
исполнителей.
3. Составить 2 инструкции, в которых не
выполняется хотя бы одно свойство алгоритма.
Записать какие изменения нужно в них внести,
чтобы получить алгоритм.
Источник
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
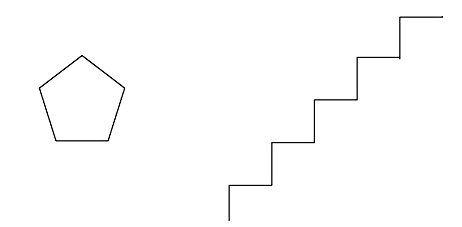
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
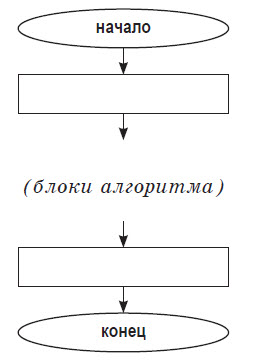
Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
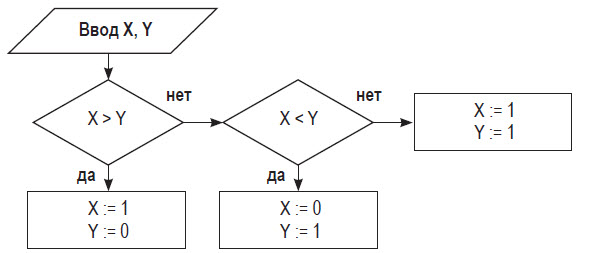
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
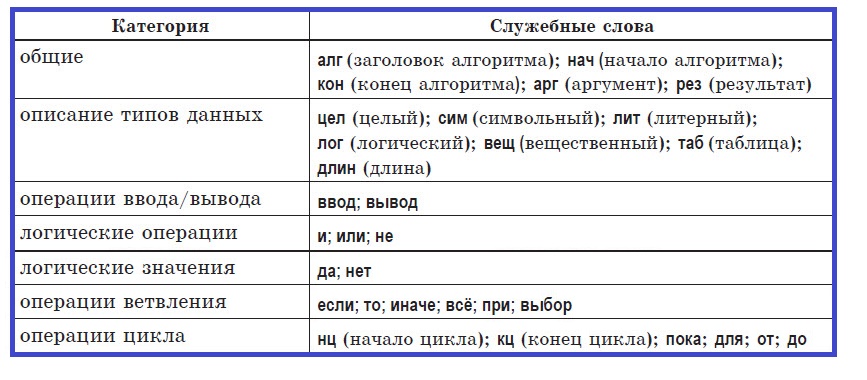
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не целым, а вещественным числом. Вещественные величины относятся к вещественному типу данных и обозначаются в учебном алгоритмическом языке служебным словом вещ. Такие величины могут отображаться двумя способами: в форме с фиксированной запятой (например, 0,0511 или –712,3456) и с плавающей запятой (те же примеры: 5,11*10-2 и –7,123456*102).
Над числовыми данными можно выполнять арифметические операции и операции сравнения.

Над целыми числами можно также выполнять две операции целочисленного деления div и mod. Операция div обозначает деление с точностью до целых чисел (остаток от деления игнорируется). Операция mod позволяет узнать остаток при делении с точностью до целых чисел. Например, результатом операции 100 div 9 будет число 11, а результатом 100 mod 9 — число 1.
Литерный тип представляет собой символы и строки, он дает возможность работать с текстом. Литерные величины — это произвольные последовательности символов. Эти последовательности заключаются в двойные кавычки: «результат», «sum_price». В качестве символов могут быть использованы буквы, цифры, знаки препинания, пробел и некоторые другие специальные знаки (возможн
