Какие прямые называются перпендикулярными каким свойством
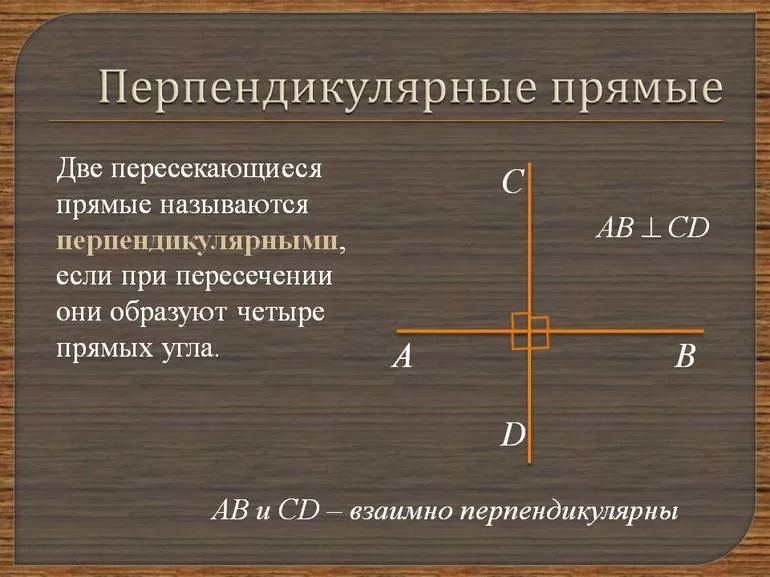

Основные свойства
При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:
- Через одну точку А можно провести только одну перпендикулярную линию основному отрезку, остальные линии будут наклонными и могут скрещиваться.
- Несколько перпендикуляров никогда не будут между собой пересекаться.
Для обозначения перпендикуляра применяется знак «⊥”. В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.
Доказательство взаимного расположения
Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:
- Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
- Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.
Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.
Определение перпендикулярности прямой и плоскости
Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.
Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

- Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
- В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.
Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.
Построение перпендикуляра
Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

- С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.
- С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.
Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:
- Одна из сторон, смежная с прямым углом, прикладывается к проведенному отрезку. На этом этапе главное — правильно совместить поверхность инструмента с ранее отложенной линией. Незначительное отклонение может привести к изменению угла.
- Проводится откладывание вертикального отрезка.
В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.
Трехмерное пространство
В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:
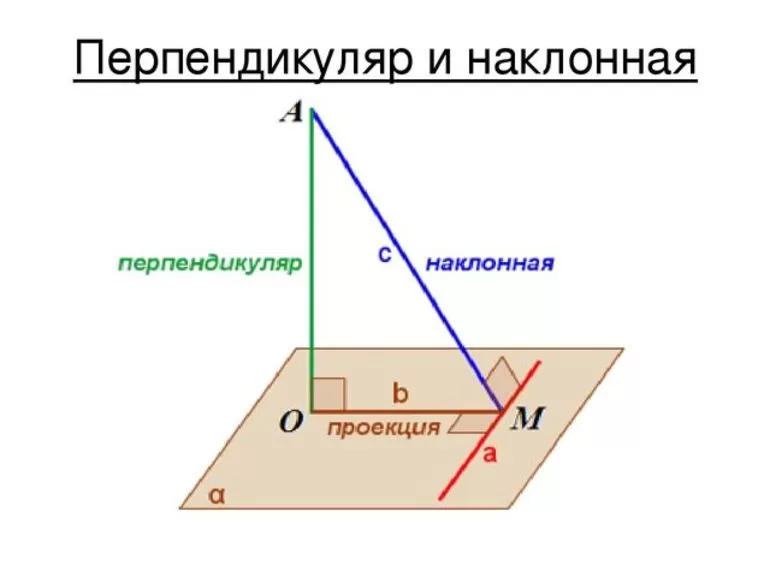
- Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости.
- Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы.
- Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.
В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.
Четырехмерная система координат и лемма
Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.
Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:
- Они должны пересекаться в точке.
- Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.
Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.
Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

- Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.
- Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.
- Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.
При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.
Применение термина
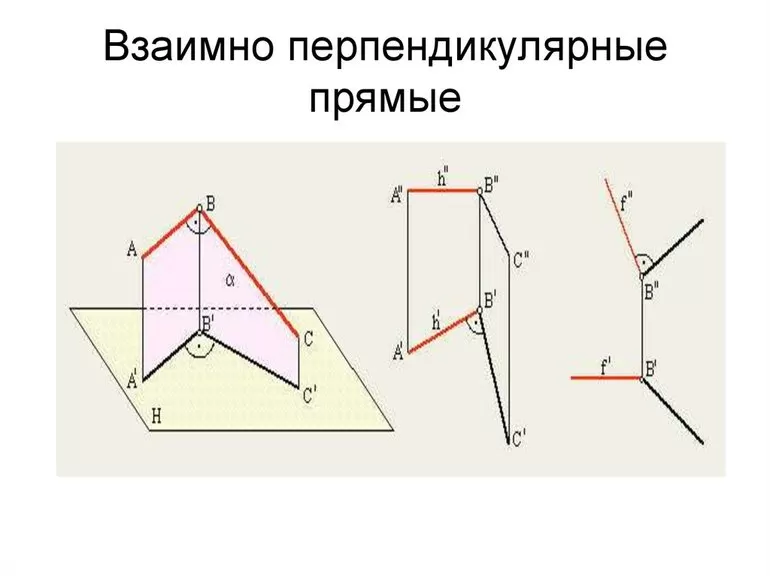
Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.
В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.
В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.
Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.
Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.
Источник
Какие прямые называются перпендикулярными
Определение
Если пара пересекающихся прямых составляют угол в 90 градусов, то такие линии имеют название перпендикулярные.
Схематично перпендикулярные линии АС и ВD будут выглядеть таким образом:

Обозначение перпендикулярных прямых в геометрии имеет такой вид:
(ACperp BD)
Признак перпендикулярности, какие условия необходимы, чему равен угол
Угол между парой пересекающихся линий в пространстве может быть прямым. В таком случае рассматриваемые прямые будут перпендикулярными.
Если угол, который образовали две скрещивающиеся прямые, будет прямым, то такие линии также будут перпендикулярными. Исходя из данного утверждения, можно заключить, что перпендикуляры на плоскости являются пересекающимися, а перпендикулярные линии в пространстве могут быть пересекающимися и скрещивающимися. Таким образом, выражения «прямые а и b перпендикулярны» и «прямые b и а перпендикулярны» можно считать равноправными. Согласно этому определению, сформулировано понятие взаимно перпендикулярных прямых.
При определении перпендикулярности линий необходимо учитывать их характеристики, которые имеют большое значение в решении задач. Основные признаки:
- Через какую-то точку А возможно начертить единственную перпендикулярную линию основному отрезку, остальные линии будут являться наклонными и могут скрещиваться.
- Несколько перпендикуляров ни при каких условиях не будут между собой пересекаться.
К примеру, можно изобразить на рисунке прямую PQ и пару линий, которые перпендикулярны ей: АА и ВВ. Необходимо доказать, что заданные прямые не имеют точек пересечения.

Подтверждение целесообразно строить с помощью метода «от обратного». Предположив, что прямые будут пересекаться в точке М1, получим какую-то точку М в другой полуплоскости, относительно прямой PQ. Таким образом, две точки пересекают две прямые, что не соответствует аксиоме. Поэтому предположение является неверным, а линии АА и ВВ не имеют точек пересечения:

Можно сделать вывод о том, что пара прямых, перпендикулярных третьей, не обладают общими точками пересечения.
Теорема о перпендикулярных прямых, как доказать
Задачи на перпендикулярные прямые, как правило, решают с учетом свойств этих линий. Доказательством перпендикулярности прямых является прямой угол, который они составляют. В том случае, когда требуется определить их перпендикулярность при известных уравнениях прямоугольной системы координат, следует применить необходимое и достаточное условие перпендикулярности линий.
Теорема 1
Теорема 1
Для того чтобы прямые a и b являлись перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.
Подтверждением данной теоремы является определение направляющего вектора прямой и перпендикулярности линий.
Допустим, что имеется прямоугольная декартовая система координат Оху, на которой заданы уравнения для прямой на плоскости, определяющие линии а и b. Направляющие векторы, характерные для данных прямых а и b, можно обозначить, как:
(vec{a}) и (vec{b})
Согласно формуле прямых а и b, необходимым и достаточным условием является перпендикулярность векторов (vec{a}) и (vec{b}.)
Данное утверждение справедливо в том случае, когда скалярное произведение векторов:
(vec{a}=(a_{x};a_{y})) и (vec{b}=(b_{x};b_{y})) не равно нулю, а запись обладает таким видом:
((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0)
Таким образом, необходимое и достаточное условие перпендикулярности линий а и b, которые расположены в прямоугольной системе координат Оху на плоскости, представляет собой следующее выражение:
((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}=0)
где (vec{a}=(a_{x};a_{y})) и (vec{b}=(b_{x};b_{y})) являются направляющими векторами линий а и b.
Данную теорему целесообразно использовать в том случае, когда требуется определить координаты направляющих векторов, либо, когда известны канонические или параметрические уравнения прямых на плоскости заданных линий а и b.
Примечание
Необходимое и достаточное условие перпендикулярности прямых а и b можно применять в случае трехмерного пространства.
В данном отношении запись будет иметь такой вид:
((vec{a};vec{b})=a_{x}*b_{x}+a_{y}*b_{y}+ a_{z}*b_{z}=0)
где (vec{a}=(a_{x};a_{y}))
(vec{b}=(b_{x};b_{y}))
(vec{z}=(z_{x};z_{y}))
являются направляющими векторами прямых а и b.
Теорема 2
Теорема 2
Линии а и b на плоскости будут перпендикулярны, если нормальный вектор прямой а и вектор прямой b взаимно перпендикулярны. Данное условие считается необходимым и достаточным.
Доказательство этой теоремы заключается в применении рассматриваемого условия в том случае, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. Таким образом, имея общее уравнение прямой вида:(
A_{x}+B_{y}+C=0)
а также уравнение прямой в отрезках вида:
(frac{x}{a}+frac{y}{b}=1)
и уравнение прямой с угловым коэффициентом вида y = kx + b, координаты векторов можно определить.
В том случае, когда линия а на плоскости определена с помощью уравнения с угловым коэффициентом:
(y=k_{1}x+b_{1})
и прямая b имеет вид:
(y=k_{2}x+b_{2})
тогда координаты нормальных векторов будут следующие:
((k_{1};-1)) и ((k_{2};-1))
Условие перпендикулярности соответствует выражению:
(k_{1}*k_{2}+(-1)*(-1)=0Leftrightarrow k_{1}*k_{2}=-1)
Теорема 3
Теорема 3
Прямые а и b перпендикулярны на плоскости при необходимом и достаточном условии, при котором один из направляющих векторов этих линий будет коллинеарным нормальному вектору второй прямой.
Данное условие действует при наличии возможности определения направляющего вектора одной прямой и координат нормального вектора другой. Одна прямая должна быть задана каноническим или параметрическим уравнением, а другая представлена в виде общего уравнения прямой, уравнением в отрезках или уравнением с угловым коэффициентом.
Источник
В статье рассматривается вопрос о перпендикулярных прямых на плоскости и трехмерном пространстве. Определение перпендикулярных прямых и их обозначения с приведенными примерами подробно разберем. Рассмотрим условия применения необходимого и достаточного условия перпендикулярности двух прямых и подробно рассмотрим на примере.
Перпендикулярные прямые – основные сведения
Угол между пересекающимися прямыми в пространстве может быть прямым. Тогда говорят, что данные прямые перпендикулярные. Когда угол между скрещивающимися прямыми прямой, тогда прямые также являются перпендикулярными. Отсюда следует, что перпендикулярные прямые на плоскости пересекающиеся, а перпендикулярные прямые пространства могут быть пересекающимися и скрещивающимися.
То есть понятия «прямые a и b перпендикулярны» и «прямые b и a перпендикулярны» считаются равноправными. Отсюда и взялось понятие взаимно перпендикулярные прямые. Обобщив вышесказанное, рассмотрим определение.
Определение 1
Две прямые называют перпендикулярными, если угол при их пересечении дает 90 градусов.
Перпендикулярность обозначается «⊥», а запись принимает вид a⊥b, что значит, прямая a перпендикулярна прямой b.
Например, перпендикулярными прямыми на плоскости могут быть стороны квадрата с общей вершиной. В трехмерном пространстве прямые Ox, Oz, Oy перпендикулярны попарно: Ox и Oz, Ox и Oy, Oy и Oz.
Перпендикулярность прямых – условия перпендикулярности
Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством. Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым.
Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.
Теорема 1
Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b.
Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.
Доказательство 1
Пусть введена прямоугольная декартова система координат Оху с заданными уравнениями прямой на плоскости, которые определяют прямые a и b. Направляющие векторы прямых a и b обозначим a→ и b→. Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов a→ и b→. Это возможно только при скалярном произведении векторов a→=(ax, ay) и b→=(bx, by) равном нулю, а запись имеет вид a→, b→=ax·bx+ay·by=0. Получим, что необходимым и достаточным условием перпендикулярности прямых a и b, находящихся в прямоугольной системе координат Оху на плоскости, является a→, b→=ax·bx+ay·by=0, где a→=(ax, ay) и b→=bx, by – это направляющие векторы прямых a и b.
Условие применимо, когда необходимо найти координаты направляющих векторов или при наличии канонических или параметрических уравнений прямых на плоскости заданных прямых a и b.
Пример 1
Заданы три точки A (8, 6), B(6, 3), C(2, 10) в прямоугольной системе координат Оху. Определить, прямые АВ и АС перпендикулярны или нет.
Решение
Прямые АВ и АС имеют направляющие векторы AB→ и AC→ соответственно. Для начала вычислим AB→=(-2, -3), AC→=(-6, 4). Получим, что векторы AB→ и AC→ перпендикулярны из свойства о скалярном произведении векторов, равном нулю.
AB→, AC→=(-2)·(-6)+(-3)·4=0
Очевидно, что необходимое и достаточное условие выполнимо, значит, АВ и АС перпендикулярны.
Ответ: прямые перпендикулярны.
Пример 2
Определить, заданные прямые x-12=y-73 и x=1+λy=2-2·λ перпендикулярны или нет.
Решение
a→=(2, 3) является направляющим вектором заданной прямой x-12=y-73,
b→=(1, -2) является направляющим вектором прямой x=1+λy=2-2·λ.
Перейдем к вычислению скалярного произведения векторов a→ и b→. Выражение будет записано:
a→,b→=2·1+3·-2=2-6≠0
Результат произведения не равен нулю, можно сделать вывод, что векторы не перпендикулярны, значит и прямые также не перпендикулярны.
Ответ: прямые не перпендикулярны.
Необходимое и достаточное условие перпендикулярности прямых a и b применяется для трехмерного пространства, записывается в виде a→, b→=ax·bx+ay·by+az·bz=0, где a→=(ax, ay, az) и b→=(bx, by, bz) являются направляющими векторами прямых a и b.
Пример 3
Проверить перпендикулярность прямых в прямоугольной системе координат трехмерного пространства, заданные уравнениями x2=y-1=z+10 и x=λy=1+2·λz=4·λ
Решение
Знаменатели из канонических уравнений прямых считаются координатами направляющего вектора прямой. Координаты направляющего вектора из параметрического уравнения – коэффициенты. Отсюда следует, что a→=(2, -1, 0) и b→=(1, 2, 4) являются направляющими векторами заданных прямых. Для выявления их перпендикулярности найдем скалярное произведение векторов.
Выражение примет вид a→,b→=2·1+(-1)·2+0·4=0.
Векторы перпендикулярны, так как произведение равно нулю. Необходимое и достаточное условие выполнено, значит прямые также перпендикулярны.
Ответ: прямые перпендикулярны.
Проверка перпендикулярности может проводится, исходя из других необходимых и достаточных условий перпендикулярности.
Теорема 2
Прямые a и b на плоскости считаются перпендикулярными при перпендикулярности нормального вектора прямой a с вектором b, это и есть необходимое и достаточное условие.
Доказательство 2
Данное условие применимо, когда уравнения прямых дают быстрое нахождение координат нормальных векторов заданных прямых. То есть при наличии общего уравнения прямой вида Ax+By+C=0, уравнения прямой в отрезках вида xa+yb=1, уравнения прямой с угловым коэффициентом вида y=kx+b координаты векторов возможно найти.
Пример 4
Выяснить, перпендикулярны ли прямые 3x-y+2=0 и x32+y12=1.
Решение
Исходя их уравнений, необходимо найти координаты нормальных векторов прямых. Получим, что nα→=(3, -1) – это нормальный вектор для прямой 3x-y+2=0.
Упростим уравнение x32+y12=1 до вида 23x+2y-1=0. Теперь четко видны координаты нормального вектора, которые запишем в такой форме nb→=23, 2.
Векторы na→=(3, -1) и nb→=23, 2 будут перпендикулярными, так как их скалярное произведение даст в итоге значение равное 0. Получим na→, nb→=3·23+(-1)·2=0.
Необходимое и достаточное условие было выполнено.
Ответ: прямые перпендикулярны.
Когда прямая a на плоскости определена при помощи уравнения с угловым коэффициентом y=k1x+b1, а прямая b – y=k2x+b2, отсюда следует, что нормальные векторы будут иметь координаты (k1, -1) и (k2, -1). Само условие перпендикулярности сводится к k1·k2+(-1)·(-1)=0⇔k1·k2=-1.
Пример 5
Выяснить, перпендикулярны ли прямые y=-37x и y=73x-12.
Решение
Прямая y=-37x имеет угловой коэффициент, равный -37, а прямая y=73x-12- 73.
Произведение угловых коэффициентов дает значение -1, -37·73=-1, то есть прямые являются перпендикулярными.
Ответ: заданные прямые перпендикулярны.
Имеется еще одно условие, используемое для определения перпендикулярности прямых на плоскости.
Теорема 3
Для перпендикулярности прямых a и b на плоскости необходимым и достаточным условием является коллинеарность направляющего вектора одной из прямых с нормальным вектором второй прямой.
Доказательство 3
Условие применимо, когда есть возможность нахождения направляющего вектора одной прямой и координат нормального вектора другой. Иначе говоря, одна прямая задается каноническим или параметрическим уравнением, а другая общим уравнением прямой, уравнением в отрезках или уравнением прямой с угловым коэффициентом.
Пример 6
Определить, являются ли заданные прямые x-y-1=0 и x0=y-42 перпендикулярными.
Решение
Получаем, что нормальный вектор прямой x-y-1=0 имеет координаты na→=(1, -1), а b→=(0, 2) – направляющий вектор прямой x0=y-42.
Отсюда видно, что векторы na→=(1, -1) и b→=(0, 2) не коллинеарны, потому что условие коллинеарности не выполняется. Не существует такого числа t, чтобы выполнялось равенство na→=t·b→. Отсюда вывод, что прямые не являются перпендикулярными.
Ответ: прямые не перпендикулярны.
Источник
