Какие основные свойства поверхностной пленки жидкости
Вещество, находящееся в жидком состоянии, характеризуется крайне плотным расположением молекул друг относительно друга. Отличаясь от твердых кристаллических тел, чьи молекулы формируют упорядоченные структуры по всему объему кристалла и ограничены в своих тепловых колебаниях фиксированными центрами, молекулы жидкости обладают значительной степенью свободы. Любая конкретная молекула жидкого вещества, как это происходит и в твердых телах, «зажата» соседними молекулами и может совершать тепловые колебания поблизости с некоторым положением равновесия. Несмотря на это, в какой-то момент, любая молекула может переместиться на соседнее вакантное место. Подобные перемещения в жидкостях происходят довольно часто, благодаря чему молекулы не привязаны к конкретным центрам, как в кристаллах, а имеют возможность перемещаться по всему объему жидкости. Именно на этом факте основывается текучесть жидкостей.
Определение 1
По причине сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные, то есть неустойчивые, упорядоченные группы, включающие в себя несколько молекул. Данное явление носит название ближнего порядка (рис. 3.5.1).
Рисунок 3.5.1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед.
Свойства жидкостей
На рисунке 3.5.2, на примере воды, проиллюстрировано различие между газообразным веществом и жидкостью. Молекула воды H2O включает в свой состав один атом кислорода и два атома водорода, которые расположены под углом 104°. В среднем, расстояние между молекулами пара в десятки раз больше, чем между молекулами воды. На рисунке 3.5.2, в отличие от рисунка 3.5.1, на котором молекулы воды представляют из себя шарики, дается представление о структуре молекулы воды.
Рисунок 3.5.2.Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·107 раз.
Сжимаемость жидкостей, то есть изменение объема вещества при изменении давления, по причине плотности расположения молекул в десятки и сотни тысяч раз меньше, чем сжимаемость газов. К примеру, чтобы изменить объем воды всего на 1 % необходимо повысить значение давления примерно в 200 раз. Подобное увеличение давления по сравнению с атмосферным достигается на глубине близкой к 2 км.
Подобно твердым телам, жидкости имеют свойство менять свой объем при изменении температуры. В случае не самых больших интервалов температур относительное изменение объема ΔVV0 пропорционально изменению температуры ΔT, что может быть записано в виде следующего соотношения:
ΔVV0=β∆T.
В котором коэффициент β представляет собой температурный коэффициент объемного расширения. Данный коэффициент у жидкостей в десятки раз превышает значение такого же у твердых тел.
Пример 1
К примеру, у воды в случае, если температура равна 20 °С βв≈2·10–4 К–1, у стали βст≈3,6·10–5 К–1, у кварцевого стекла βкв≈9·10–6 К–1.
Тепловое расширение воды обладает важным для жизни на Земле эффектом. В условиях температуры ниже 4 °С вода начинает расширяется при снижении температуры β<0. Максимальную плотность ρв=103 кг/м3 вода приобретает при температуре 4 °С.
Замерзая, вода расширяется, из-за чего лед продолжает плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом эквивалентна величине в 0 °С. У дна водоема, то есть слоях воды, обладающих большей плотностью, температура держится около 4 °С.
Поверхностное натяжение
Наличие свободной поверхности в жидкостях является одной из самых интересных ее особенностей. В отличие от газов, жидкость не заполняет весь объем сосуда, в котором она находится. Между жидкостью и газом, возможно паром, возникает граница раздела, находящаяся в особых условиях по сравнению с остальной массой жидкости. В отличие от молекул в глубине жидкости, молекулы, располагающиеся в пограничном ее слое, окружены другими молекулами этой же жидкости не со всех сторон. В среднем воздействующие на одну из молекул внутри жидкости со стороны соседних молекул силы межмолекулярного взаимодействия взаимно скомпенсированы. Каждая отдельно взятая молекула в пограничном слое притягивается находящимися внутри жидкости молекулами. При этом, силами, которые оказывают воздействие на такую молекулу жидкости со стороны молекул газа можно пренебречь. Вследствие этого возникает некая направленная вглубь жидкости равнодействующая сила. Поверхностные молекулы втягиваются внутрь жидкости, с помощью действия сил межмолекулярного притяжения. Однако все молекулы, в том числе и принадлежащие пограничному слою, должны находиться в состоянии равновесия. Оно достигается за счет сокращения расстояния между молекулами в пограничном слое и ближайшими их соседями в жидкости. Как проиллюстрировано на рисунке 3.1.2, в процессе уменьшения расстояния расстояния между молекулами появляются силы отталкивания. В случае, когда средняя величина расстояния между молекулами в жидкости равна r0, молекулы поверхностного слоя расположены плотнее, и по этой причине по сравнению с внутренними молекулами они имеют дополнительным запас потенциальной энергии, что можно увидеть на рисунке 3.1.2.
Замечание 1
Стоит обратить внимание на то, что более плотного поверхностного слоя не приводит к сколь-нибудь заметному изменению объема жидкости по причине чрезвычайно низкой сжимаемости.
Силы межмолекулярного взаимодействия совершают положительную работу, в случае, когда молекула перемещается с поверхности внутрь жидкости. И наоборот, чтобы достать некоторое количество молекул на поверхность из глубины жидкости, то есть повысить площадь поверхности жидкости, внешним силам необходимо произвести пропорциональную изменению ΔS площади поверхности положительную работу ΔAвнеш:
ΔAвнеш=σ∆S,
где коэффициент σ носит название коэффициента поверхностного натяжения (σ>0).
Определение 2
Из всего вышесказанного следует, что коэффициент поверхностного натяжения – это величина равная работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или же в ньютонах на метр (1 Н/м=1 Дж/м2).
Таким образом, по сравнению с молекулами внутри жидкости молекулы поверхностного слоя жидкости обладают избыточной потенциальной энергией. Потенциальная энергия Eр поверхности жидкости пропорциональна ее площади и выражается в виде следующей формулы:
Eр=Aвнеш=σS.
Из раздела механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Следовательно, свободная поверхность жидкости стремится уменьшить свою площадь. По данной причине свободная капля жидкости принимает шарообразную форму.
Определение 3
Жидкость ведет себя таким образом, будто по касательной к ее поверхности действуют сокращающие данную поверхность силы. Такие силы называются силами поверхностного натяжения.
Силы поверхностного натяжения влияют на поверхность жидкости таким образом, что она становится похожей на упругую растянутую пленку, с той лишь разницей, что упругие силы в пленке зависят от площади ее поверхности, то есть от степени деформированности пленки, а силы поверхностного натяжения, зависимости от площади поверхности жидкости не имеют.
Пример 2
Некоторые жидкости, например, мыльная вода, имеют способность формировать тонкие пленки. Хорошо известные каждому человеку мыльные пузыри обладают правильной сферической формой, в чем также проявляется воздействие сил поверхностного натяжения. В случае, когда в мыльный раствор опускают проволочную рамку с одной подвижной стороной, вся она затягивается пленкой жидкости, как это показано на рисунке 3.5.3.
Рисунок 3.5.3. Подвижная сторона проволочной рамки в равновесии под действием внешней силы Fвн→ и результирующей сил поверхностного натяжения Fн→.
Силы поверхностного натяжения действуют на уменьшение поверхности пленки. Ради равновесия подвижной стороны рамки к ней необходимо приложить внешнюю силу
Fвн→=-Fн→. Если воздействие силы Fвн→ спровоцирует перемещение перекладины на некоторое Δx, то будет произведена работа ΔAвн=FвнΔx=ΔEp=σΔS, где ΔS=2LΔx является увеличением площади поверхности обеих сторон мыльной пленки. По той причине, что модули сил Fвн→ и Fн→ эквивалентны, справедливой будет запись:
Fн∆x=σ2L∆x или σ=Fн2L.
Определение 4
Исходя из этого, можно заявить, что коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
По причине воздействия сил поверхностного натяжения на капли жидкости и их действия внутри мыльных пузырей появляется некоторое избыточное давление Δp. При мысленном разрезании сферической капли с радиусом R на две равные части каждая из половин должна находиться в равновесии под действием приложенных к границе разреза длиной 2πR и сил избыточного давления, действующих на площадь πR2 сечения (рис. 3.5.4) сил поверхностного натяжения. Условие равновесия может быть записано в следующем виде:
σ2πR=∆pπR2.
Исходя из этого, можно заявить, что избыточное давление внутри капли эквивалентно:
∆p=2σR(капля жидкости).
Рисунок 3.5.4.Сечение сферической капли жидкости.
Из-за того, что пленка обладает двумя поверхностями, величина избыточного давления внутри мыльного пузыря в два раза выше, чем в капле:
∆p=4σR(мыльный пузырь).
Пренебрегая взаимодействием с молекулами газа, можно сказать, что поблизости с границей между твердым телом, жидкостью и газом форма свободной поверхности жидкости зависима от сил взаимодействия молекул жидкости с молекулами твердого тела.
Определение 5
В случае, когда данные силы превышают силы взаимодействия между молекулами жидкости, жидкость смачивает поверхность твердого тела. В таком случае жидкость подходит к поверхности твердого тела под некоторым характерным для данной пары жидкость – твердое тело острым углом θ. Такой угол носит название краевого угла.
Краевой угол θ является тупым (рисунок 3.5.5), в случае, если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела. В подобном случае можно сказать, что поверхность твердого тела не смачивается жидкостью. В условиях полного смачивания θ=0, полного несмачивания θ=180°.
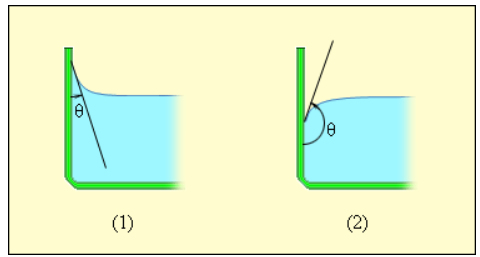
Рисунок 3.5.5. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей.
Капиллярные явления
Определение 6
Капиллярными явлениями называют процесс подъема или опускания жидкости в трубках малого диаметра, другими словами, в капиллярах.
Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. На рисунке 3.5.6 проиллюстрирована опущенная нижним концом в смачивающую жидкость плотности ρ капиллярная трубка, обладающая некоторым радиусом r. При этом верхний конец капилляра является открытым. Подъем жидкости в капилляре будет происходить до тех пор, пока сила тяжести Fт→, оказывающая воздействие на столб жидкости в капилляре, не станет эквивалентна по модулю результирующей Fндействующих вдоль границы соприкосновения жидкости с поверхностью капилляра сил поверхностного натяжения: Fт=Fн, где Fт=mg=ρhπr2g, Fн=σ2πr cos θ.
Из этого следует:
h=2σ cos θρgr.
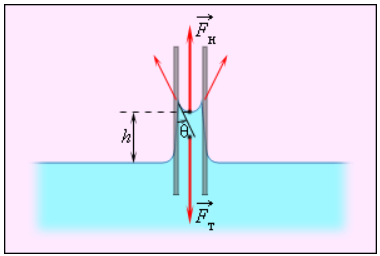
Рисунок 3.5.6. Подъем смачивающей жидкости в капилляре.
При полном смачивании θ=0, cos θ=1. В таком случае:
h=2σρgr.
При полном несмачивании θ=180°, cos θ=–1 и, соответственно, h<0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
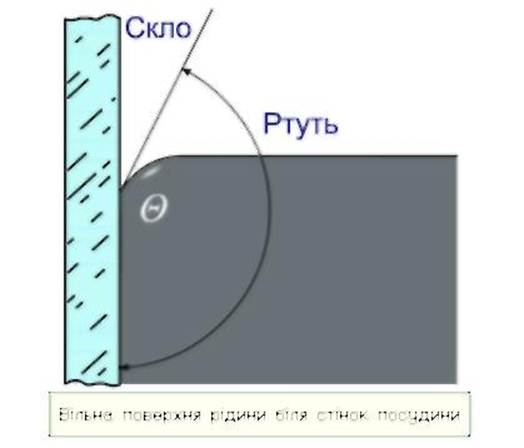
Вода почти полностью смачивает чистую поверхность стекла. Ртуть же, строго наоборот, полностью не смачивает стеклянную поверхность. По этой причине уровень ртути в стеклянном капилляре опускается ниже, чем уровень в сосуде.
Источник
ПОВЕРХНОСТНое НАТЯжение
Характерным свойством жидкости является наличие свободной поверхности раздела Жидкость-газ, Которая расположена перпендикулярно к направлению силы притяжения. Поверхностный слой жидкости имеет особенные свойства, что предопределяет существование так называемых Поверхностных явлений.
Сравним молекулу, которая находится в объеме жидкости, с молекулой поверхностного слоя.
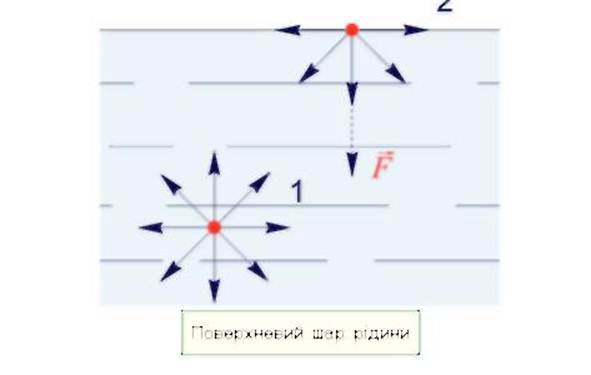
Поверхностным натяжением Называется работа, которую необходимо выполнить для изотермического увеличения илощи поверхности жидкости:
Где — Коэффициент поверхностного натяжения;
— Увеличение площади поверхности жидкости.
Коэффициент поверхностного натяжения…. численно равняется силе поверхностного натяжения F, Которая действует по касательной к поверхности жидкости и приходится на единицу длины граници жидкости.
Поверхностным натягом объясняются такие характерные для жидкого состояния вещества явления, как образование пены, формирования капель и тому подобное.
В существовании сил поверхностного натяжения можно убедиться на опыте с мыльной пленкой.

Коэффициент поверхностного натяжения Не зависит От величины и формы поверхности жидкости, а Зависит От сил молекулярного взаимодействия (природы жидкости) и потому имеет разные значения для разных жидкостей. Например, у жидкостей, которые легко испаряющиеся (эфир, спирт, бензин) молекулярные силы и, соответственно, поверхностный натяг значительно меньше, чем у ртути и других жидких металлов. Определение коэффициента поверхностного натяжения осуществляется экспериментально.

Дуже важливою є залежність коефіцієнта поверхневого натягу від температури, яку вперше дослідив Д. Менделєєв у 1860 р. При підвищенні температури рідини поверхневий натяг послаблюється, а при наближенні до критичної — прямує до нуля.
Для зменшення поверхневого натягу у рідину додаються спеціальні домішки, які розташовуються на поверхні і зменшують поверхневу енергію. Такі речовини називають Поверхнево-активними речовинами (ПАР). До них належать різні компоненти нафти, мило, деякі жирні кислоти, спирти, ефіри, амінокислоти, миючі засоби. Зменшення О У розчинах ПАР зумовлене підвищенням їх концентрації в поверхневому шарі, тобто Адсорбцією.
Очень важной является зависимость коэффициента поверхностного натяжения от температуры, которую впервые исследовал Д. Менделеев в 1860 г. При повышении температуры жидкости поверхностный натяг ослабляется, а при приближении к критической — приближается к нулю.
Для уменьшения поверхностного натяжения в жидкость добавляются специальные примеси, которые располагаются на поверхности и уменьшают поверхностную энергию. Такие вещества называют Поверхностно-активными веществами (ПАВ). К ним принадлежат разные компоненты нефти, мыло, некоторые жирные кислоты, спирты, эфиры, аминокислоты, моющие средства. Уменьшение … В растворах ПАВ предопределено повышением их концентрации в поверхностном слое, то есть Адсорбцией.
СМАЧИВАНИЕ. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ
Важную роль в процессе исследования контактного взаимодействия жидкости с твердым телом играет явление смачивания.
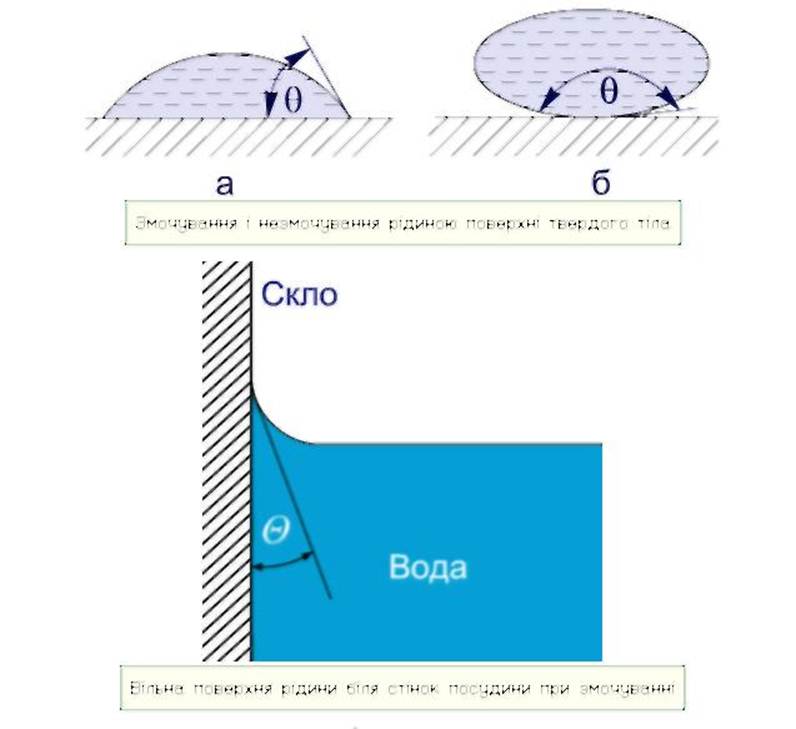

Выясним условия, за которых имеют место явления смачивания или несмачивания. Для этого выполним простые опыты.
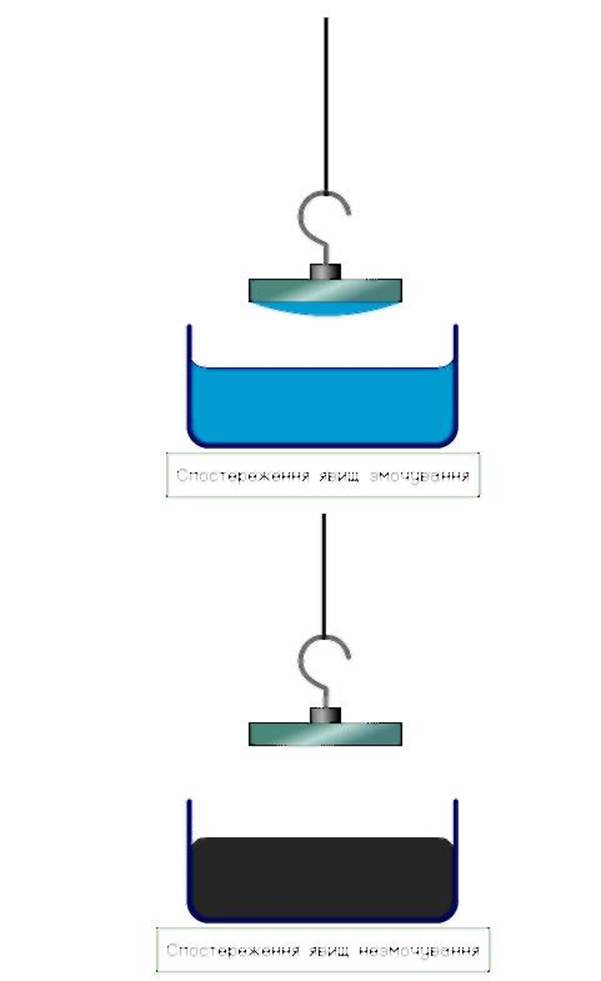
Следовательно, явления смачивания и несмачивания объясняются соотношением между силами притяжения молекул твердых тел и жидкостей и силами межмолекулярного притяжения в жидкостях. Если силы притяжения между молекулами твердого тела и жидкости превосходят силы притяжения между молекулами жидкости, то жидкость Смачивает Твердое тело. Если межмолекулярное притяжение в жидкости превышает силы притяжения молекул жидкости к молекулам твердого тела, то жидкость Не смачивает Твердое тело.
В природе часто встречаются пористые тела, объем которых пронизан большим количеством мелких каналов. Такое строение имеют бумага, кожа, дерево, почва, некоторые строительные материалы. Вода или другая жидкость при попадании на такое тело впитывается в него или поднимается на значительную высоту. Аналогичные явления можно наблюдать также в очень узких стеклянных трубках с диаметром около миллиметра и меньше, которые называются капиллярами.
Явления, которые определены поверхностным натягом и происходят в тонких трубчатых каналах (капиллярах), называются капиллярными явлениями или капиллярностью.
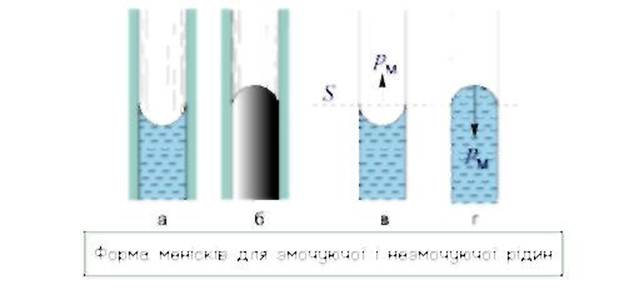
Викривлена поверхня рідини створює додатковий тиск на рідину порівняно з тиском під плоскою поверхнею. При увігнутому меніску тиск під плоскою поверхнею S Зменшується На величину додаткового тиску Рм. При опуклому меніску додатковий тиск Ри Збільшує той тиск, який існує під плоскою поверхнею рідини, зокрема, атмосферний тиск на вільну поверхню рідини.
Додатковий тиск для сферичної поверхні рідини розраховується за формулою:
Рм” Т1
Де А — Коефіцієнт поверхневого натягу, R — Радіус сферичної поверхні; Рм < 0, якщо меніск увігнутий; Рм > 0, якщо меніск опуклий.
Ця формула називається Формулою Лапласа На честь видатного французького астронома, математика і фізика П’єра Симона Лапласа, який вперше її отримав.
Встановимо деякі закономірності капілярних явищ.
Искривлённая поверхность жидкости создает дополнительное давление на жидкость сравнительно с давлением под плоской поверхностью. При вогнутом мениске давление под плоской поверхностью S уменьшается На величину дополнительного давления ….. При выпуклом мениске дополнительное давление …. увеличивает то давление, которое существует под плоской поверхностью жидкости, в частности, атмосферное давление на свободную поверхность жидкости.
Дополнительное давление для сферической поверхности жидкости рассчитывается по формуле:
Где а — коэффициент поверхностного натяжения,
R — радиус сферической поверхности;
Рм < 0, если мениск вогнут; рм > 0, если мениск выпукл.
Эта формула называется формулой Лапласа в честь выдающегося французского астронома, математика и физика Пъера Симона Лапласа, который впервые ее получил.
Установим некоторые закономерности капиллярных явлений.

Если имеет место явление смачивания, то Жидкость в капиллярах устанавливается выше от уровня жидкости в широкой трубке, а высота поднятия жидкости является наибольшей в капилляре с меньшим радиусом.
Если имеет место явление смачивания, то Жидкость в капиллярах устанавливается выше от уровня жидкости в широкой трубке, а высота поднятия жидкости является наибольшей в капилляре с меньшим радиусом.

Когда имеет место явление несмачивания, Жидкость в капиллярах устанавливается ниже от уровня жидкости в широкой трубке, а снижение уровня жидкости является наибольшим в капилляре с меньшим радиусом.
Для подъема жидкости в капилляре имеет место Закон Жюрена.
Высота поднятия жидкости в капилляре пропорциональна коэффициенту поверхностного натяжения жидкости и обратно Пропорциональная радиусу капилляра и плотности жидкости.
Следовательно, Ее …….
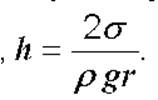
Формула Жюрена застосовна і до капілярної трубки із незмочуючою рідиною, але у цьому випадку обчислюється не висота підняття рідини, а зниження її рівня.
Формулу Жюрена можна використати для визначення коефіцієнту поверхневого натягу А. Для цього необхідно лише точно виміряти висоту підняття H і радіус капіляра Г. Тоді за відомими значеннями Р І G з формули Жюрена одержується значення А. Це один з найбільш поширених методів визначення коефіцієнту поверхневого натягу рідини.
Формула Жюрена применима и к капиллярной трубке с несмачивающей жидкостью, но в этом случае вычисляется не высота поднятия жидкости, а снижение ее уровня.
Формулу Жюрена можно использовать для определения коэффициента поверхностного натяжения …. Для этого необходимо лишь точно измерять высоту поднятия H И радиус капилляра R. Тогда за известными значениями Р И G Из формулы Жюрена получается значение ….. Это один из наиболее распространенных методов определения коэффициента поверхностного натяжения жидкости.
ЯВЛЕНИЯ СМАЧИВАНИЯ И КАПИЛЛЯРНОСТИ В ЖИВОЙ ПРИРОДЕ И ТЕХНИКЕ
Явление смачивания имеет большое практическое значение, его используют в процессах пайка, склеивание, окрашивание тел, смазывания тертевих поверхностей и тому подобное. Особенно широко применяется смачивание в Флотацийних процессах (обогащении руд ценной породой). В основу этих процессов положено изменение поверхностного натяжения жидкости с помощью разных примесей и неодинаковое смачивание ею разных твердых тел.
Сущность принципа флотации заключается в следующем. Чистая руда почти никогда не встречается в природе. Полезное ископаемое по большей части перемешано с ненужной пустой породой (бедная руда). Прежде чем использовать в производстве, ее необходимо обогатить, то есть отделить руду от породы. Флотационный процесс заключается в прилипании пузырьков воздуха к частицам полезного ископаемого. Плотность полезного ископаемого и пузырька воздуха меньше плотности воды, потому они всплывают. Следовательно, флотация возможна при таких условиях: 1) поверхность частиц полезного ископаемого не должна смачиваться водой; 2) руда должна быть раздроблена на такие частицы, чтобы они могли всплывать с пузырьками воздуха, которые к ним прилипают. Для улучшения процесса прилипания пузырьков воздуха к частицам полезного ископаемого в флотацийну ванну добавляют масло, которое смачивает частицы полезного ископаемого и не смачивает частицу породы. Пузырьки воздух хороший прилипают к покрытым тонкой пленкой масла частиц полезного ископаемого.
При механической обработке металлов, бурении скважин в горных породах их смачивают специальными жидкостями, что облегчает и убыстряет их обработку.
Явление смачивания необходимо учитывать и в конструировании космических аппаратов. В состоянии невесомости смачивающая жидкость расплывается по стенкам сосуда, а несмачивающая собирается в сосуде в виде большой капли. Поэтому материал стенок и форму емкостей для топлива нужно выбирать так, чтобы топливо содержалось около отверстий, сквозь которые оно перекачивается к двигателям.
Чрезвычайно распространенная в природе, технике и быту капиллярность, которая играет значительную роль во многих процессах.
В частности, в строительной практике необходимо учитывать поднятие влаги по капиллярам строительных материалов. Кирпич и бетон имеют широко разветвленные системы капилляров, по которых вода может подниматься на значительную высоту, вызывая влажность стен дома. Для защиты стен от влажности между фундаментом дома и стенами прокладывают слой толи, смолы или другого материала, который препятствует проникновению влаги.
Капиллярные явления важны и в жизни растений, людей и животных (в теле взрослого человека приблизительно 1 60 миллиардов капилляров, общая длина которых 60 — 80 тысяч км). Именно в капиллярах происходят основные процессы, связанные с дыханием и питанием организмов.
На капиллярных явлениях основываются агротехнические приемы регуляции водного режима почвы — прикатывание и боронование.
Явление капиллярности используют и в быту, например при применении гигроскопической ваты, промокательной бумаги, полотенец и салфеток.
Метки:
Источник
