Какие основные свойства ядер
Основными характеристиками атомных ядер являются электрический заряд, масса, спин, энергия связи и так далее.
Заряд ядра
Ядро каждого из атомов обладает положительным зарядом. В качестве носителя положительного заряда выступает протон. По той причине, что заряд протона численно эквивалентен заряду электрона e, можно записать, что заряд ядра элемента равен +Ze (Z выражает собой целое число, которое указывает на порядковый номер химического элемента в периодической системе химических элементов Д. И. Менделеева). Значение Z также характеризует число протонов, входящих в состав ядра и количество электронов в атоме. Именно из-за этого его определяют как атомный номер ядра. Электрический заряд представляет собой одну из основных характеристик атомного ядра, от которой зависят оптические, химические и иные свойства атомов.
Масса ядра
Существует также другая значимая характеристика ядра, а именно масса. Массу атомов и ядер принято выражать в атомных единицах массы (а.е.м.), в качестве атомной единицы массы выступает 112 массы нуклида углерода C612:
где NA=6,022·1023 моль-1 обозначает число Авогадро.
Кроме того, есть другой способ выражения атомной массы: исходя из соотношения Эйнштейна E=mc2, ее выражают в единицах энергии. По той причине, что масса протона mp=1.00728 а.е.м.=938,28 МэВ, масса нейтрона mn=1.00866а.е.м.=939,57МэВ, а масса электрона me=5,49⋅10-4 а.е.м.=0,511МэВ,
Из приведенных выше значений видно, что масса электрона несущественно мала, если сравнивать ее с массой ядра, поэтому масса ядра практически эквивалентна массе всего атома и отлична от целых чисел.
Определение 1
Масса ядра, которая выражается в а.е.м. и округляется до целого числа носит название массового числа и обозначается с помощью буквы A. Она характеризует количество нуклонов, находящихся в составе ядра.
Количество нейтронов в ядре эквивалентно N=A−Z. В качестве обозначения ядер используют символ XZA, в котором X определяется как химический символ этого элемента.
Определение 2
Атомные ядра, обладающие одинаковым числом протонов, однако при этом отличающимися друг от друга массовыми числами, носят название изотопов.
В некоторых элементах количество стабильных и нестабильных изотопов достигает десятков, в качестве примера, уран обладает 14 изотопами: от U92227 до U92240. Большая часть химических элементов, которые существуют в природе, являются смесью нескольких изотопов. Как раз наличие изотопов объясняет следующее явление: некоторые природные элементы обладают массой, которая является отличной от целых чисел. В качестве примера рассмотрим природный хлор, который состоит из 75%C1735l и 24%C1737l, а его атомная масса эквивалентна 35,5 а.е.м. В большей части атомов, исключая водород, изотопы обладают практически равными физическими и химическими свойствами. Однако, за своими, исключительно ядерными свойствами, изотопы значительно отличаются друг от друга. Какие-то из них могут представлять собой стабильные изотопы, а другие – радиоактивные.
Определение 3
Ядра с эквивалентными массовыми числами, но отличающимися значениями Z носят название изобар, в качестве примера, A1840r, C2040a.
Определение 4
Ядра с одинаковым числом нейтронов определяют как изотоны.
Определение 5
Среди легких ядер встречаются и так называемые «зеркальные» пары ядер. Это такие пары ядер, в которых числа Z и A−Z меняются местами. В качестве примера подобных ядер можно привести C613 и N713 или H13 и H23e.
Размер атомного ядра
Принимая форму атомного ядра приблизительно сферической, мы имеем возможность ввести понятие его радиуса R. Обратим внимание на то, что в некоторых ядрах есть небольшое отклонение от симметрии в распределении электрического заряда. Более того, атомные ядра представляют собой не статические, а динамические системы, и понятие радиуса ядра нельзя представлять как радиус шара. Именно из-за этого факта, в качестве размеров атомного ядра нужно принимать ту область, в которой проявляются ядерные силы. В процессе создания количественной теории рассеивания α-частиц Э. Резерфорд исходил из тех предположений, что атомное ядро и α – частица взаимодействуют по закону Кулона, Другими словами из того, что электрическое поле вокруг ядра обладает сферической симметрией.
Это работает в отношении α – частиц, обладающих достаточно малым значением энергии E. При этом частица не имеет возможности преодолеть кулоновский потенциальный барьер и в последствии не достигает области, в которой наблюдается действие ядерных сил. Одновременно с повышением энергии частицы до некоторого граничного значения Eгр, α-частица достигает данной границы. В таком случае в рассеянии α-частиц возникает некоторое отклонение от формулы Резерфорда.
Опытным путем было определено, что радиус R ядра является зависимым от числа нуклонов, которые входят в состав ядра.
Размеры ядер определяют экспериментальным путем по рассеянию протонов, быстрых нейтронов или же электронов высоких энергий. Существует также целый список иных косвенных способов получения значений размеров ядер. Они основываются:
- на связи времени жизни α – радиоактивных ядер с энергией выпущенных ими α – частиц;
- на оптических свойствах, носящих название мезоатомов, в которых один из электронов временно захвачен мюоном;
- на сравнении энергий связи парных зеркальных атомов.
Данные способы подтверждают эмпирическую зависимость R=R0A1/3, а также благодаря таким измерениям определено значение постоянной R0=1,2-1,5·10-15 м. Обратим свое внимание также на тот факт, что за единицу расстояний в атомной физике и физике элементарных частиц принимают единицу измерения «ферми», которая равняется 10-15 м 1 ф=10-15 м. Радиусы атомных ядер определяются их массовым числом и находятся в промежутке от 2·10-15 до 10-14 м. Если из формулы R=R0A1/3 выразить R0 и записать его в следующем виде 4πR33A=const, то можно заметить, что на каждый нуклон приходится примерно одинаковый объем. Из данного факта можно сделать вывод о том, что плотность ядерного вещества для всех ядер так же приблизительно одинакова. Как можно заметить, плотность ядерного вещества довольно велика. Этот факт основывается на действие ядерных сил.
Энергия связи. Дефект масс ядер
Определение 6
Величину ∆m, что определяет разницу масс между массой нуклонов, которые формируют ядро, и массой ядра, называют дефектом массы ядра.
Важные сведения о свойствах ядра могут быть получены даже при отсутствии знаний о подробностях взаимодействия между нуклонами ядра, на основании закона сохранения энергии и закона пропорциональности массы и энергии. Поскольку в результате каждого изменения массы ∆m происходит соответствующее изменение энергии ∆E(∆E=∆mc2), то при образовании ядра выделяется некоторое количество энергии. Исходя из закона сохранения энергии можно сделать вывод о том, что ровно такое же количество энергии необходимо для того, чтобы разделить ядро на составляющие его элементы, другими словами отдалить нуклоны друг от друга на такие расстояния, при которых взаимодействия между ними не происходит. Данную энергию определяют как энергию связи ядра.
Замечание 1
Заметим, что данная формула довольно неудобная в применении, так как в таблицах приводиться не массы ядер, а массы, которые относятся к массам нейтральных атомов. По этой причине ради удобства вычислений формулу преобразуют таким образом, чтобы в нее входили не массы атомов, а массы ядер. Для достижения этой цели в правой части формулы добавим и отнимем массу Z электронов (me). В таком случае Eсв=Zmp+me+A-Zmn-mя+Zmec2=ZmH11+A-Zmn-mac2 — масса атома водорода, ma — масса атома.
В ядерной физике энергию зачастую выражают в мегаэлектрон-вольтах (МэВ). Если речь идет о практическом применении ядерной энергии, то ее измеряют в джоулях. В случае сравнения энергии двух ядер используют массовую единицу энергии — соотношение между массой и энергией (E=mc2). Массовая единица энергии (le) равняется энергии, что соответствует массе в одну а.е.м. Она равняется 931,502 МэВ.
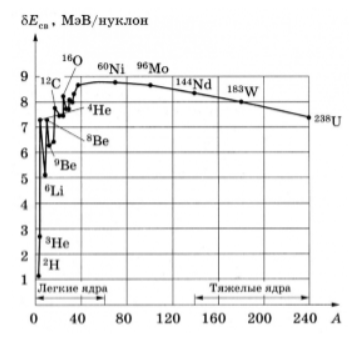
Рисунок 1
Определение 7
Кроме энергии, важное значение имеет удельная энергия связи ядра — энергия связи, которая припадает на один нуклон: ω=Ecв/A. Эта величина меняется сравнительно медленно по сравнению со сменой массового числа A, имея почти постоянную величину 8.6 МэВ в средней части периодической системы и уменьшается до ее краев.
Дефект массы
Энергия связи в МэВ: Eсв=∆m·931,502=0,030359·931,502=28,3 МэВ;
Удельная энергия связи: ω=EсвA=28,3 МэВ4≈7.1 МэВ.
Источник
Свойства атомных ядер
Перечислим основные характеристики ядер, которые будут
обсуждаться далее:
- Размеры ядер.
- Энергия связи нуклонов в ядре и энергии отделения нуклонов и кластеров от
ядра. - Спин ядра и моменты импульсов составляющих ядро нуклонов.
- Четность ядра и частиц.
- Изоспин ядра и нуклонов.
- Спектры ядер. Характеристики основного и возбужденных состояний.
- Электромагнитные свойства ядра и нуклонов.
Размеры ядер
Распределение заряда и массы в атомных ядрах исследуется в
экспериментах по упругому рассеянию на ядрах α-частиц
(исторически это первые эксперименты Резерфорда), электронов и протонов.
Выяснилось, что как плотность распределения заряда, так и плотность
распределения массы ядра приближенно выражаются распределением Ферми:
(9.1) |
Величину R называют радиусом ядра. Отметим, что поскольку распределение
плотности заряда и массы близки, но не совпадают друг с другом, отличаются также
и зарядовый и массовый радиусы. В дальнейшем будут даны примеры и рассмотрены
причины различия этих величин. В приближенных расчетах можно считать эти
величины совпадающими и полагать, что радиус ядра
Rr0A1/3 | (9.2) |
Это одновременно означает независимость средней плотности ядра от
массового числа. Действительно, оценим плотность ядра с числом А
нуклонов:
(9.3) |
Величина r01.2-1.3
Фм. Из (9.3) получим плотность ядерной материи ρ2·1014 г/см3
сближения -частицы и ядра золота при бомбардировке
мишени из золота пучком α-частиц
с кинетическими энергиями 22 МэВ. Сравнить результат с суммой радиусов ядер
золота и гелия.
При лобовом соударении налетающей частицы и ядра золота кинетическая энергия
Т -частицы
целиком тратится на преодоление потенциального кулоновского барьера:
RHe+ RAu = r0(41/3
+ 1971/3)10 Фм
При кинетических энергиях α-частиц 22
МэВ и выше расстояние наибольшего сближения ядер гелия и золота начинает быть
сравнимым с размерами ядерных систем. Это означает, что чисто кулоновское
рассеяние, отраженное знаменитой формулой Резерфорда, не исчерпывает
взаимодействие нуклонов. При больших энергиях в формулу Резерфорда вводят еще
один множитель – формфактор, отражающий размеры и внутреннюю структуру
сталкивающихся нуклонов. Результат решения данной задачи показывает, что
введение формфактора необходимо при кинетических энергиях -частицы,
превышающих 22 МэВ.
В данном примере умножение и деление на константу конверсии
позволяет избежать введения явного вида квадрата единичного заряда, используя
вместо него хорошо известную величину – постоянную тонкой структуры e2/c = 1/137.
При оценке радиусов распределения заряда в ядре (кулоновского
радиуса) используют различие энергий связи двух ядер-изобар (т.е. ядер с
одинаковым числом нуклонов А).
Задача 9.2. Из сравнения энергий связи зеркальных
ядер 11В и 11С (E = 2.765
МэВ) оценить величину r0 в формуле (2.2) для радиусов ядер.
Для равномерно заряженной сферы кулоновская энергия равна:
Отсюда для величины r0 получаем
(Заметим, что в числовом решении этой задачи очень удобным является умножение
числителя и знаменателя на константу конверсии, что позволяет использовать
постоянную тонкой структуры e2/c = 1/137
и не переходить к другой системе единиц.)
Задача 9.3. Из сравнения энергий связи ядер 3H
и 3He (Е = 0.76 МэВ) оценить кулоновский радиус
R 3He.
Действуя аналогично задаче 5, получим для кулоновского
радиуса 2.3 Фм.
Энергии связи и массы ядер
Масса стабильных ядер меньше суммы масс входящих в ядро
нуклонов, разность этих величин и определяет энергию связи ядра:
Eb(A,Z) = Zmp + (A – | (9.4) |
В (9.4) MN – масса ядра. В таблицах масс приводятся, как правило,
не массы ядер, а массы нейтральных атомов либо величины, с ними связанные. Часто
массы нейтральных атомов приводят в единицах
1u = M(12C)/12 = 931.5 МэВ/с2. | (9.5) |
В приложении к [1] приведены значения “избытков масс”
= M – A, где М – масса нейтрального атома в МэВ. Величина А представляет собой в
данном случае произведение числа нуклонов на значение единицы массы (9.5) в МэВ.
Таким образом, величины приводятся в единицах МэВ, что очень удобно
для проведения расчетов.
Задача 9.4. Вычислить удельную энергию связи для
ядра 12С.
Для примера вычислим величину энергии связи и удельной
энергии связи ядра 12С двумя способами: а) пользуясь таблицей масс в
единицах (9.5) и б) используя таблицу = M – A.
Прежде всего необходимо преобразовать формулу (9.4), заменив
массы ядер MN на массы нейтральных атомов М:
M(A,Z) = MN(A,Z) + Zme. | (9.6) |
Формула (9.6) является приближенной – в ней опущены энергии связи электронов
в атомах. Однако поскольку энергии связи нуклонов в ядре на 5 – 6 порядков
превышают энергии связи электронов в атомах, это приближение не скажется на
точности дальнейших расчетов энергий связи ядер. Прибавляя и вычитая Zme
в (9.6), получим для энергии связи нуклонов в ядрах
Eb = ZM(1H) + (A – | (9.7) |
Для ядра 12С по первому способу
Eb = (6.1.007825 + 6.1.008665
– 12.000000).931.5 = 92.16 МэВ.
Для использования таблиц для = M – A
преобразуем (9.7)
Eb = ZM(1H) + (A – | (9.8) |
Для энергии связи 12С расчет этим способом проще:
6.7.289 + 6.8.071 = 92.16 МэВ.
Поэтому в дальнейших расчетах будет использоваться именно второй способ,
основанный на таблицах для избытков масс .
Удельная энергия связи, т.е. энергия связи на один нуклон, для ядра 12С
составляет
ε = Eb/A = 92.16/12 = | (9.9) |
Распределение удельных энергий связи как функция числа
нуклонов А является наиболее важным для приложений экспериментальным результатом
физики ядра. Теоретическое объяснение этого распределения дает модель заряженной
жидкой капли и соответствующая этой модели формула Вайцзеккера.
Задача 9.5. Найти энергии отделения нейтрона и
протона от ядра 12С.
Энергия отделения нейтрона
Bn = M(A-1,Z) + mn – M(A,Z) = (A-1,Z) + n – (A,Z).
Bn(12C) = 10.650 + 8.071 = 18.72 МэВ.
Энергия отделения протона
Bp = M(A-1,Z-1) + M(1H) – M(A,Z) = (A-1,Z-1) + (1H)
– (A,Z).
Bp(12C) = 8.668 + 7.289 = 15.96 МэВ.
Задача 9.6. Найти энергию отделения альфа-частицы от
12С.
Ba = M(A-4,Z-2) + M(4He) – M(A,Z) = (A-4,Z-2) + (4He)
– (A,Z).
Ba(12C) = 4.941 + 2.424 = 7.365 МэВ.
Сравним результаты, полученные для удельной энергии связи
ядра 12С и энергий отделения от него нейтрона, протона и
альфа-частицы. Энергия отделения одного нуклона от этого ядра оказалась более
чем вдвое выше удельной энергии связи! Энергия одновременного отделения кластера
из 4 нуклонов – альфа-частицы оказалась меньше удельной энергии связи – т.е.
средней энергии отделения одного нуклона. Эти факты и аналогичные результаты для
ряда других ядер были объяснены в теоретической модели ядерных оболочек (См.
далее семинары 11,12)
Спин ядра и моменты нуклонов
Основное и возбужденные состояния ядра и других квантовых
систем характеризуется значениями моментов количества движения. Если ядро близко
к сферическому, соответствующий ему гамильтониан коммутирует с оператором
квадрата момента, что означает, что собственные значения этого оператора
являются “хорошими квантовыми числами”, т.е. сохраняются. Как правило, ядерный
гамильтониан коммутирует также с оператором проекции момента на одну из осей (в
качестве этой оси обычно выбирают ось z):
[,2] | (9.10) |
Все перечисленные операторы действуют в пространстве волновых функций ядра ?:
Спином ядра называется максимальное значение проекции собственного момента
импульса на выделенную ось, т.е. величина J. Спины и моменты частиц и ядер
измеряются в единицах . Спин нуклона,
т.е.его момент в системе координат, связанной с ним, равен 1/2.
Полный момент количества движения нуклона в ядре складывается
из его спина и орбитального момента относительно центра ядра:
Спин ядра – результат сложения моментов нуклонов ядра:
. | (9.13) |
Сложение квантовых векторов происходит по правилам, изложенным на Семинаре 5
-формула (5.6). Напомним еще раз, что результаты сложения квантовых векторов
отличаются от результатов сложения векторов в классической физике. Квантовый
вектор может пробегать лишь дискретный ряд значений (через единицу).
Задача 9.7. Найти возможные значения полного момента
j нейтрона с орбитальным моментом 3. Определить для каждого значения полного
момента все возможные значения проекции на выделенную ось.
Для j = 5/2 mj = -5/2, -3/2, -1/2, +1/2, +3/2, +5/2. (6 значений, 6 =
2(5/2) + 1).
Для j = 7/2 mj= -7/2, -5/2, -3/2, -1/2, +1/2, +3/2, +5/2, +7/2 (8
значений, 8 = 2(7/2) + 1).
Число возможных проекций момента j на выделенную ось Nj = 2j + 1.
Задача 9.8. Определить возможные значения спина
ядра, состоящего из двух протонов и двух нейтронов в состояниях с
орбитальными моментами, равными нулю. Считать все нуклоны находящимися в
одном (низшем из возможных) энергетическом состоянии.
Поскольку полные моменты всех нуклонов в данном случае равны по 1/2,
возможные значения суммы четырех векторов
Однако в физике реализуется только первое из этих значений,
т.е.0. Здесь проявляется действие принципа Паули. Согласно принципу Паули,
фермионы любой системы должны находиться в разных квантовых состояниях. Иными
словами, фермионы не могут иметь совпадающие наборы квантовых чисел. В данном
случае два нейтрона с одинаковой энергией и одинаковыми (нулевыми) значениями
орбитального момента должны иметь разные значения проекции спина на
выделенную ось, т.е. +1/2 и –1/2. Сумма спинов нейтронов в этом случае равна
0. Эта же ситуация реализуется для двух протонов. Поэтому суммарный момент такой
четверки нуклонов – т.е. ядра 4 Не – равен 0.
Четность состояний ядра
Волновая функция ядра является функцией координат
составляющих его нуклонов. Переход от выбранной системы координат к системе,
соответствующей зеркальному отражению всех координатных осей, приводит к
преобразованию волновой функции системы. Оператор пространственного отражения
Если гамильтониан системы коммутирует с оператором
пространственного отражения, четность системы является “хорошим квантовым
числом”, т.е. сохраняется. Для сильных и электромагнитных взаимодействий это
выполняется, поэтому (с точностью до малых добавок, связанных со слабыми
взаимодействиями) ядерные состояния имеют определенную четность. Принято
указывать одновременно спин и четность ядерного состояния в форме JP.
Например, в основном состоянии дейтрона (системы нейтрон-протон) JP = 1+.
Четность системы частиц является произведением собственных четностей частиц и
четности, соответствующей их орбитальному движению. Собственная четность
нуклонов +1. Четность орбитального движения частицы с орбитальным моментом l
равна (-1)l.
Для системы нуклонов
Задача 9.9. Доказать, что орбитальный момент
дейтрона может принимать только два значения: 0 либо 2.
Для дейтрона JP=1+. Четность
дейтрона положительна, (-1)L = 1, следовательно L – четное число.
Спин дейтрона равен 1. Суммарный спин двух нуклонов может принимать значения
либо 0, либо 1.
=1.
Четному значению орбитального момента может соответствовать только суммарный
спин 1. Поэтому значение орбитального момента есть результат вычитания (или
сложения, что в случае векторов идентично) вектора полного момента и вектора
спина: = + = 0, 2.
Изоспин ядра и нуклонов
Как основное, так и возбужденные состояния ядер – помимо
рассмотренных ранее энергии, спина и четности– характеризуются квантовыми
числами, которые называются изоспином
и проекцией изоспина. ( В литературе эти
квантовые числа обозначаются обычно либо символами T и Tz, либо I и Iz
).
Введение этих квантовых чисел связано с тем фактом, что
ядерные силы инвариантны относительно замены протонов на нейтроны. Это
особенно ярко проявляется в спектрах т.н.”зеркальных” ядер, т.е. ядер–изобар, у которых
число протонов одного равно числу нейтронов другого. (См., например, спектры
ядер 13C и 13N). Для всех известных пар таких ядер имеет
место подобие спектров низших возбужденных состояний: спины и четности низших
состояний одинаковы, а энергии возбуждения близки.
С точки зрения теории изоспина, нейтрон и протон являются
одной и той же частицей – нуклоном с изоспином I = 1/2 – в двух разных
состояниях, различающихся проекцией изоспина на выделенную ось (Iz = I3)
в пространстве изоспина. Таких проекций для момента
I = 1/2 может быть только две: Iz = +1/2 (протон) и Iz =
–1/2 (нейтрон). (Квантовая теория изоспина построена по аналогии с теорией
спина. Однако пространство изоспина не совпадает с обычным координатным
пространством.)
Система Z протонов и N нейтронов – ядро – имеет проекцию
изоспина
Iz(A,Z) = Z(+1/2) + N(-1/2) = | (9.17) |
Изоспин системы нуклонов является векторной суммой
изоспинов составляющих:
(9.18) |
Ядерные (т.е.сильные) взаимодействия не зависят от проекции изоспина, или,
точнее, сильные взаимодействия инвариантны относительно вращений в
изоспиновом пространстве.
Однако от величины изоспина ядерные силы зависят! Низшим по энергии
состояниям системы нуклонов, т.е. основным состоянием ядра, является состояние с
низшим возможным значением изоспина, которое равно
I0 = |Iz| = |(Z – | (9.19) |
Возбужденные состояния ядер могут иметь более высокие значения изоспина, но с
той же проекцией. Таким образом, характеристиками уровней данного ядра являются
энергия, спин состояния, четность состояния и изоспин. Обычно три последних
квантовых числа указываются как JP, I.
Задача 9.10. Определить изоспин основного состояния
и проекцию изоспина для ядра
48Ca.
Ядро 48 Ca имеет 20 протонов и 28 нейтронов.
Следовательно, проекция изоспина этого ядра равна Iz = (20-28)/2 =
-4. Изоспин основного состояния I= |Iz | = 4. Частицы или
системы частиц, имеющие одинаковый изоспин и разные проекции изоспина,
составляют изоспиновые мультиплеты (дублеты,
триплеты, и т.д.). Особенностью членов такого мультиплета является то, что они
одинаковым образом участвуют в сильном взаимодействии. Простейший пример дублета
– нейтрон и протон. Состояния зеркальных ядер 13C и 13N
являются другим примером.
Задание 4
- Определить энергии связи и удельные энергии связи ядер 4He,
7Li, 12C, 13C, 27Al. - Для ядер задачи 1 рассчитать энергии отделения нейтрона и протона.
- Вывести формулу, связывающую энергию связи и избыток массы М-А ядра.
- Сравнить энергии отделения протона, нейтрона и альфа-частицы от ядра
16O. - При какой кинетической энергии частицы ее длина волны становится равной
диаметру ядра 27Al? Рассмотреть два случая: а) электрон; b)
нейтрон. - Найти кинетические энергии протона и электрона с приведенными длинами волн
1 Фм. - Определить максимальную длину волны -кванта
в реакции + 12С11С
+ n. . - Найти возможные значения полного момента атома, если спин ядра атома равен
5/2, а момент электронной оболочки составляет 3/2. Для каждого значения
полного момента j указать возможные значения проекций моментов mj. - Рассчитать магнитный момент системы нейтрон-протон в состоянии 3S1.
Сравнить результат с экспериментально найденным значением магнитного момента
дейтрона (0.86 ядерных магнетонов). - Рассчитать электрический квадрупольный момент сферически симметричного
ядра или частицы. - Четность дейтрона равна +1. Спин дейтрона равен 1. Найти возможные
значения орбитального момента системы протон-нейтрон в дейтроне. - Найти значения изоспина ядер 208 Pb, 197Au и
209Bi в основных состояниях. - Рассчитать величину кинетической энергии, выделяющейся в результате
термоядерной реакции 2H + 3H4He
+ n. - В рамках капельной модели ядра рассчитать вклады отдельных членов в
суммарную энергию связи для двух ядер: с А>200 и A<100. - На схеме уровней нуклона в потенциале трехмерного осциллятора со
спин-орбитальным взаимодействием изобразить конфигурационные структуры
основных состояний ядер 4He,12C и 16O.
Перечислить квантовые числа нуклонов, формирующих ядра задачи 15. - В одночастичной оболочечной модели получить спины и четности основных
состояний следующих ядер:5He, 13C, 17O,
17F, 29Si,
33S, 3He, 11C, 15N, 27Al. - Указать конфигурационную структуру ядер 57Ni,
58Ni, 59Ni, 60Ni. Обосновать результат
сравнением с экспериментальными данными о спинах и четностях этих ядер.
Источник
