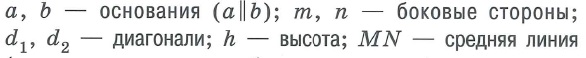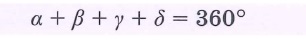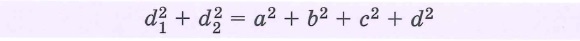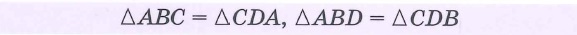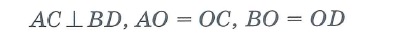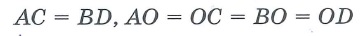Какие общие свойства у ромба и квадрата
Автор:
02 апреля 2019 08:28
Мы все учили в школе геометрию, но с годами многое подзабыли. Чтобы не попасть впросак, когда ваш ребенок спросит, чем ромб отличается от квадрата, почитайте эту статью и вспомните, казалось бы, давно забытое.

Источник:
Очень часто четкое определение какого-либо предмета дает о нем практически полную информацию. Вот, например, ромб и квадрат – едва ли не самые распространенные геометрические фигуры. Глядя на них, мы понимаем, что они отличаются, но вот чем и как это объяснить простыми словами? Давайте разбираться.
Что представляет собой ромб
Источник:
Геометрия дает такое определение ромба: «Ромбом называется параллелограмм…». Стоп, сначала придется вспомнить, что такое параллелограмм. Это многоугольник с четырьмя углами, у которого противоположные стороны параллельны. А какими же свойствами обладает ромб как разновидность параллелограмма? Вот они:
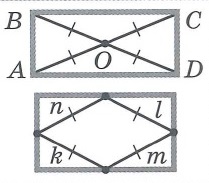
1. Если соединить противоположные углы ромба диагоналями, то углы их пересечения составят 90º, то есть они взаимно перпендикулярны.
2. Эти диагонали (вообще-то в строгой науке геометрии принято говорить «отрезки диагоналей ромба») лежат на биссектрисах, делящих его углы пополам (помните школьный стишок: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам»? Ребенку тоже будет полезно).
Что представляет собой квадрат
Источник:
С квадратом все намного проще, его определение звучит так: квадрат – это прямоугольник, у которого все стороны равны. Теперь нужно определить, что такое прямоугольник. Это тоже параллелограмм, как и ромб, но с прямыми углами, то есть равными 90º.
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?

Источник:
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Источник:
Ссылки по теме:

Понравился пост? Поддержи Фишки, нажми:
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Ромб и квадрат
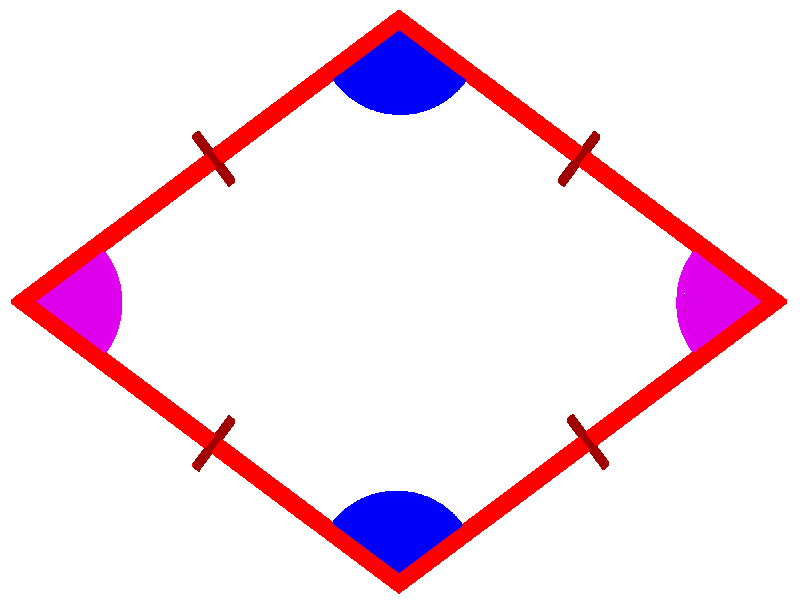
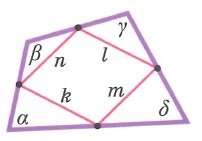
Частным видом параллелограмма является ромб.
Ромбом называется параллелограмм, у которого все стороны равны
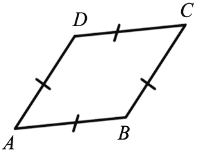
ABCD – ромб.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба
Доказательство
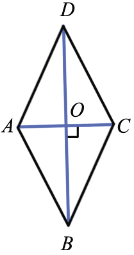
Дано: ABCD – ромб
Доказать: AC BD,
BD,  ADO =
ADO =  CDO
CDO
Доказательство:
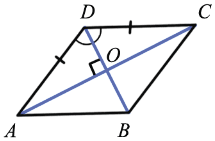
AD = DC (по определению ромба), значит,  ADC – равнобедренный.
ADC – равнобедренный.
AO = OC (по свойству диагоналей параллелограмма),  DO – медиана
DO – медиана  ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,
ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,  AC
AC BD,
BD,  ADO =
ADO =  CDO, что и требовалось доказать.
CDO, что и требовалось доказать.
Теорема
Доказательство
Дано: ABCD – параллелограмм, AC BD
BD
Доказать: ABCD – ромб
Доказательство:
Рассмотрим  AOВ и
AOВ и  COВ:
COВ:
Т.к. AC BD, то
BD, то AOВ =
AOВ =  COВ = 900;
COВ = 900;
AO = OC (по свойству диагоналей параллелограмма), ОВ – общий катет, 
 AOВ =
AOВ =  COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,
COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,  ВС = ВА.
ВС = ВА.
В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD – параллелограмм (по условию) AD = BC =AB = DC (по доказанному).  ABCD – ромб, что и требовалось доказать.
ABCD – ромб, что и требовалось доказать.
Теорема
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм – ромб
Доказательство
Дано: ABCD – параллелограмм, АС – диагональ и биссектриса  DAB и
DAB и DCB
DCB
Доказать: ABCD – ромб
Доказательство:
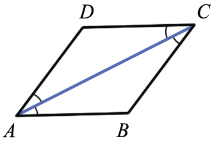
 DAB =
DAB = DCB (по свойству параллелограмма), а АС -биссектриса
DCB (по свойству параллелограмма), а АС -биссектриса  DAB и
DAB и DCB (т.е. АС делит эти углы на два равных угла),
DCB (т.е. АС делит эти углы на два равных угла), 
 DAC =
DAC =  BAC =
BAC = DCA =
DCA =  BCA
BCA
Рассмотрим  ADC:
ADC:  DAC =
DAC = DCA,
DCA, 
 ADC – равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,
ADC – равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD – параллелограмм (по условию) AD = BC =AB = DC (по доказанному).  ABCD – ромб, что и требовалось доказать.
ABCD – ромб, что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками ромба.
Основные свойства квадрата:
1. Все углы квадрата прямые.
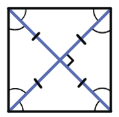
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Многоугольник
Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Трапеция
Прямоугольник
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 422,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 446,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 494,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 513,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 562,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 568,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 823,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 851,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 980,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 997,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
Конспект урока. 8 класс (учебник Л.С.Атанасян)
Тема урока: Ромб, квадрат и их свойства
Тип урока:
1) по основной дидактической цели: урок открытия нового знания.
2) по основному способу проведения: сочетание различных форм занятий.
3)по форме проведения: комбинированный урок.
Цели урока: Создание условий для усвоения учащимися понятий ромба, квадрата, их свойств.
Задачи урока:
1) образовательные:
Формировать:
-понятия ромба и квадрата как частных видов параллелограмма;
-умение формулировать свойства ромба, квадрата;
-умение построения ромба и квадрата;
-умения применять свойства ромба и квадрата при решении задач.
2) Развивающие:
-Развивать мышление, память, математический язык, осуществлять самостоятельную деятельность на уроке.
-Развивать умения систематизировать полученные знания.
-Развивать умение высказывать свое мнение, делать выводы;
Формы обучения: индивидуальная, фронтальная, групповая.
Оборудование: доска, мультимедиа, карточки с заданиями, раздаточный материал с заданиями.
План урока:
I . Организационный момент
II. Актуализация опорных знаний
III. Формирование новых знаний
IV. Применение знаний, формирование умений и навыков.
V. Теоретическая самостоятельная работа.
VI. Постановка домашнего задания
VII. Подведение итогов урока
VIII. Рефлексия
I. Организационный момент
Приветствие. Проверка готовности к уроку.
2. Мотивация учебной деятельности учащихся.
II. Актуализация опорных знаний.
Мы с вами изучили свойства и признаки некоторых четырехугольников. Перед вами лист с четырехугольниками. Какие четырехугольники из изображенных на листе вы знаете? Для каких четырехугольников знаете точные определения и свойства? А какие известны по форме, но определения и свойств этих свойств не знаете? Да это квадрат и ромб, с понятием квадрата вы встречались ещё в начальной школе, да и ромб фигура- знакома.
Чтобы узнать их определения и свойства нам не обойтись без знаний полученных ранее. Мы их проверим, выполнив следующую работу. Возьмите лист № 1. На листе вопросы. Если вы согласны с предложением ставьте «да», если не согласны ставьте «нет». Ответы появятся на доске через 3 мин. Если появляются вопросы у учащихся, то на них отвечают или учащиеся или учитель. Приводятся примеры.
п/п
Вопрос
Данет
Является ли прямоугольником параллелограмм, у которого есть прямой угол?
Верно ли, что каждый прямоугольник является параллелограммом?
Верно ли, что каждый параллелограмм является прямоугольником?
Диагонали параллелограмма равны 4 и 5 дм. Является ли этот параллелограмм прямоугольником?
Диагонали четырехугольника равны. Обязательно ли этот четырехугольник прямоугольник?
6.
Верно ли, что в каждом четырехугольнике сумма углов составляет 3600.
7.
Верно ли, что в каждом четырехугольнике сумма соседних углов равна 1800
8.
Верно ли, что в каждом четырехугольнике противоположные углы равны.
III. Формирование новых знаний.
Сегодня Вам предстоит самостоятельно изучить новый материал. Сейчас откроете учебник на стр.109. Читая текст, вы делает пометки на полях: слайд 4
V – уже знал;
+ – новое;
– – думал иначе;
? – не понял, есть вопросы.
Затем вам предстоит заполнить таблицу, это лист №2. Записи делайте краткие, ключевые слова, фразы.
Лист №2
Определения
Свойства, особые свойства.
ромб
1.
2.
3.
4.
5.
6.
квадрат
1.
2.
3.
4.
5.
6.
Кстати: Ромб (от греч.) бубен. Если сейчас бубны делают круглой формы, то раньше их делали как раз в форме ромба. От тех времен дошли ромбики на картах.
После заполнения учащимися таблицы обобщаем результаты работы в режиме беседы. Даются определения, перечисляются свойства фигур (ромба, квадрата), находят общие свойства. Если у обучающихся возникли вопросы, то отвечаю на них, предварительно выяснив, не может ли кто-то из обучающихся ответить на возникший вопрос. ( Этот приём способствует развитию умения классифицировать, систематизировать поступающую информацию, выделять новое.)
Конечно, при решении задач на уроках так и в жизни используются свойства фигур.
Например: Ромб, в котором проведены диагонали, считается одной из самых крепких и выносливых конструкций. Такую конструкцию очень широко используют для постройки мостов, зданий, и даже, для рамы мотоцикла.
Вы выяснили, каким особым свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. Нам необходимо доказать это свойство. Работа в парах. Задача пар: прочитать доказательство, определить основную идею. Желающие доказывают у доски, остальные учащиеся следят за доказательством, задают вопросы.
IV. Применение знаний, формирование умений и навыков.
Теперь зная свойства ромба, решите задачу. Два ученика решают у доски.
Задача1 .
Найдите периметр ромба ABCD, если ∟ В =120 ◦, а диагональ BD = 20 см. (Ответ: 20 см) рис.на доске. Наводящие вопросы:
– Что называют периметром?
– Как найти периметр ромба?
– Каким свойством обладают диагонали ромба?
– Свойства равностороннего треугольника?
Задача 2. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 300 меньше другого. Чертёж сделать самостоятельно. (Ответ: 300 и 600).
После решения идет обсуждение решённых задач.
V. Теоретическая самостоятельная работа.
– Заполните таблицу, отметив знаки + (да) и – (нет).
Лист № 3.
параллелограмм
прямоугольник
ромб
ввадрат
1.
Все стороны равны
2.
Все углы равны
3.
Противоположные стороны параллельны и равны
4.
Противоположные углы равны
5.
Сумма соседних углов равна 1800
6.
Все углы прямые
7.
Диагонали равны
8.
Диагонали пересекаются и точкой пресечения делятся пополам.
9.
Диагонали являются биссектрисами углов
10.
Диагонали взаимно перпендикулярны
параллелограмм
прямоугольник
ромб
квадрат
1.
Все стороны равны
_
_
+
+
2.
Все углы равны
_
+
+
3.
Противоположные стороны параллельны и равны
+
+
+
+
4.
Противоположные углы равны
+
+
+
+
5.
Сумма соседних углов равна 1800
+
+
+
+
6.
Все углы прямые
_
+
_
+
7.
Диагонали равны
_
+
_
+
8.
Диагонали пересекаются и точкой пресечения делятся пополам.
+
+
+
+
9.
Диагонали являются биссектрисами углов
_
_
+
+
10.
Диагонали взаимно перпендикулярны
_
_
+
+
Самостоятельную проверить и поставьте себе оценку.
Критерии выставления оценки:
Оценка «5» – все ответы верные.
Оценка «4» – допущены 1, 2 ошибки.
Оценка «3» – допущены 3-5 ошибки.
Оценка «2» – допущены более 5 ошибок.
VI. Домашнее задание: 1. п.п.47. Выучить определения и свойства ромба и квадрата. Уметь доказывать теорему, выражающую особое свойство ромба. №№ 406,407.
VII. Подведение итогов урока
Выставить оценки за работу на уроке наиболее активным учащимся и кто выполнил
работу по уровням.
VIII. Рефлексия.
Важна ли сегодняшняя тема урока. Если да, то обоснуйте.
Какие новые понятия изучили?
Что узнали нового и чему научились на уроке?
Чтобы хотели узнать ещё по данной теме?
Источник
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды четырехугольников: | |||
|  | ||
|  | ||
|  | ||
|  | ||
|  | ||
Свойства произвольных четырехугольников: | |||
|  | ||
Свойства параллелограмма: | |||
| 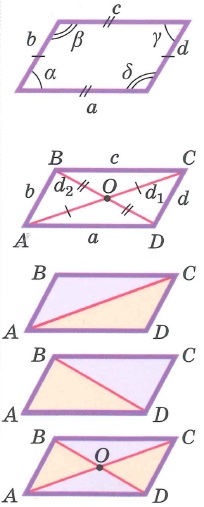 | ||
Свойства ромба: | |||
| 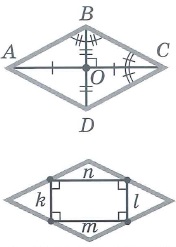 | ||
Свойства прямоугольника: | |||
|  | ||
Свойства квадрата: | |||
|  | ||
Свойства трапеции: | |||
|  | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Источник
Технологическая карта урока
Автор: Богомаз Валентина Александровна, учитель математики и информатики, государственное учреждение образования «Учебно-педагогический комплекс Полошковский детский-сад средняя школа Климовичского района»
Описание материала: предлагаю Вам технологическую карту урока по математике по теме «Ромб, квадрат. Свойства, признаки ромба и квадрата» для учащихся 8 класса. Это первый урок при изучении данной темы. Материал будет полезен для учителей, работающих в 8 классах, так как технологическая карта урока является современной формой планирования педагогического взаимодействия учителя и ученика, дающая возможность отразить деятельностную составляющую взаимодействия всех участников учебного процесса.
Ромб, квадрат. Свойства, признаки ромба и квадрата
Цель урока
Ознакомление с четырехугольниками «ромб», «квадрат», их определениями, свойствами и признаками
Задачи урока
Обучающие
Развивающие
Воспитывающие
Предметные
Содействовать усвоению понятий ромба и квадрата, их свойств и признаков, применению полученных знаний для решения прикладных задач
Способствовать развитию конструкторских навыков, умения анализировать, сравнивать, делать выводы на основе полученных результатов
Способствовать формированию познавательной самостоятельности, ответственности, сотрудничества, взаимовыручки
Метапредметные
Создать условия для формирования умений определять цели и задачи деятельности; умение находить способы решения поставленной задачи; умений планировать, контролировать и оценивать свои действия.
Планируемые результаты урока
Учащиеся должны знать:
Определение, свойства и признаки ромба и квадрата;
Практическое использование фигур в жизни человека;
Учащиеся должны уметь:
Использовать признаки и свойства фигур для решения задач практической направленности
Тип урока
Урок усвоения новых знаний
Техническое обеспечение
Геометрия: учеб. пособие для 8 кл. общеобразоват. учреждений с рус. яз. обучения / В.В. Шлыков. —3-е изд., перераб. — Минск : Нар. Асвета, 2011. — 166 с.: ил., компьютеры, раздаточный материал, оценочные листы
Время
Деятельность учителя
Деятельность учащихся
Прогнозируемый результат
Средства обучения
I этап. 1. Мотивирование к учебной деятельности
1 мин
Здравствуйте, дорогие мои. Рад вас всех видеть, садитесь, пожалуйста. Прежде чем мы начнем заниматься делом, я хотел бы, чтобы каждый из вас настроился на урок. Желаю вам удачи и новых открытий. Сегодня мы продолжим путешествие по прекрасной стране Геометрия. Пройдемся по ее памятным местам – определениям и теоремам.
Слушают учителя
Психологическая готовность учащихся к работе
2.Проверка домашнего задания.
7 мин
Работа на уроке будет оцениваться поэтапно. Обратите внимание, у вас на столах лежат оценочные листы, где прописаны все этапы урока. В листах будут отображаться результаты вашей учебной деятельности на каждом из этих этапов
К работе готовы?
Приступим.
На предыдущих уроках мы рассматривали свойства и признаки параллелограмма и прямоугольника.
Давайте, ребята, мы вместе вытащим из тайников памяти кое-что ценное и восхитимся нашими глубокими знаниями
Чтобы вы на этот миг
Не сидели грустные,
Вместе выполнить должны
Мы работу тестовую
Возьмите оценочные листы, в которые вы будете записывать ответы. Присаживайтесь за компьютеры и приступайте к работе.
(Учитель раздаёт карточки)
Возвращайтесь на свои места, самостоятельно оцените свою работу на данном этапе. Критерий оценивания – за каждый правильный ответ один балл. Внимание на монитор!
Слушают учителя, выполняют тестовую работу, проводят самооценку.
Повторение пройденного материала, выполнение теста
Презентация, оценочные листы, слайд презентации с правильными ответами на тест
3.Определение темы урока.
7 мин
На столах у вас появились кластеры, которые вы должны заполнить в парах. Приступайте.
Ребята, у нас возникли проблемы. Пока мы их решить не можем, нам не хватает знаний. Приобрести их поможет сегодняшний урок, тема которого «Ромб, квадрат. Свойства, признаки ромба и квадрата»
Откроем тетради, запишем дату, классная работа и тему урока
(в этот момент учитель записывает на доске тему урока)
Двое учащихся на предыдущем уроке получили задание подготовить мини-презентации по темам: «Ромб» и «Квадрат».
Предоставим им слово.
Заполняют кластеры, при затруднениях задают вопросы, работают в парах.
Презентуют свои работы, смотрят презентации.
Актуализация знаний об опорных понятиях
Кластеры, учитель-консультант, презентации
4.Постановка целей урока.
1 мин
Давайте вместе определим цель нашего урока
Определяют цель урока
Личностное принятие целей урока
Слайд презентации с целью
Этап 2. Реализация основных этапов урока.
1.Ознакомление с определением ромба и квадрата.
2 мин
Организует фронтальную работу с классом для актуализации имеющихся знаний и умений, создает условия, способствующие самостоятельному формулированию учащимися определений и свойств, опираясь на полученные ранее знания.
Давайте вернёмся к нашему кластеру и попробуем вместе сформулировать определения новых фигур.
-Ромб это параллелограмм, у которого …..
Квадрат это ромб, у которого…….
Квадрат это прямоугольник, у которого…
Отвечают на вопросы учителя, делают выводы, дают определения ромба и квадрата
-все стороны равны.
-все углы прямые.
-все стороны равны.
Наличие продукта инт