Какие из свойств определителя справедливы
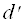
Квадратной матрице А порядка n можно сопоставить число det А (или |A|, или ), называемое ее определителем, следующим образом:
Определитель матрицы A также называют ее детерминантом. Правило вычисления детерминанта для матрицы порядка N является довольно сложным для восприятия и применения. Однако известны методы, позволяющие реализовать вычисление определителей высоких порядков на основе определителей низших порядков. Один из методов основан на свойстве разложения определителя по элементам некоторого ряда (свойство 7). При этом заметим, что определители невысоких порядков (1, 2, 3) желательно уметь вычислять согласно определению.
Вычисление определителя 2-го порядка иллюстрируется схемой:
Пример 4.1. Найти определители матриц
Решение:
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса), которое символически можно записать так:
Пример 4.2. Вычислить определитель матрицы
Решение:
det А = 5*1*(-3) + (-2)*(-4)*6 + 3*0*1 — 6*1*1 — 3*(-2)*(-3) — 0*(-4)*5 = -15+48-6-18 = 48-39 = 9.
Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.
Свойство 1 («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот. Иными словами,
В дальнейшем строки и столбцы будем просто называть рядами определителя.
Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.
Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.
Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.
Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.
Действительно,
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
Например,
Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одною ряда прибавить соответствующие элементы параллельного ряда, умноженные па любое число.
Пример 4.3. Доказать, что
Решение: Действительно, используя свойства 5, 4 и 3 подучим
Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.
Минором некоторого элемента аij определителя n-гопорядка называется определитель n — 1-го порядка, полученный из исходного путем вычеркивания строки и столбца, па пересечении которых находится выбранный элемент. Обозначается mij
Алгебраическим дополнением элемента aij определителя называется его минор, взятый со знаком «плюс», если сумма i + j четное число, и со знаком «минус», если эта сумма нечетная. Обозначается Aij :
Свойство 7 («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что
В самом деле, имеем
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.
Пример 4.4. Вычислите определитель матрицы
Решение: Для разложения определителя обычно выбирают гот ряд, где есть нулевые элементы, т. к. соответствующие им слагаемые в разложении будут равны нулю.
Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.
Так, например,
Источник
Главная >> Лекции >> Линейная алгебра >> Определители и их свойства Матричный калькулятор
Определители и их свойства. Перестановкой чисел 1, 2,…, n называется любое расположение этих чисел в определенном порядке. В элементарной алгебре доказывается, что число всех перестановок, которые можно образовать из n чисел, равно 12…n = n!. Например, из трех чисел 1, 2, 3 можно образовать 3!=6 перестановок: 123, 132, 312, 321, 231, 213. Говорят, что в данной перестановке числа i и j составляют инверсию (беспорядок), если i>j, но i стоит в этой перестановке раньше j, то есть если большее число стоит левее меньшего.
Перестановка называется четной (или нечетной), если в ней соответственно четно (нечетно) общее число инверсий. Операция, посредством которой от одной перестановки переходят к другой, составленной из тех же n чисел, называется подстановкой n-ой степени.
Подстановка, переводящая одну перестановку в другую, записывается двумя строками в общих скобках, причем числа, занимающие одинаковые места в рассматриваемых перестановках, называются соответствующими и пишутся одно под другим. Например, символ обозначает подстановку, в которой 3 переходит в 4, 1 → 2, 2 → 1, 4 → 3. Подстановка называется четной (или нечетной), если общее число инверсий в обеих строках подстановки четно (нечетно). Всякая подстановка n-ой степени может быть записана в виде ,т.е. с натуральным расположением чисел в верхней строке.
Пусть нам дана квадратная матрица порядка n
. (4.3)
Рассмотрим все возможные произведения по n элементов этой матрицы, взятых по одному и только по одному из каждой строки и каждого столбца, т.е. произведений вида:
, (4.4)
где индексы q1, q2,…,qn составляют некоторую перестановку из чисел
1, 2,…, n. Число таких произведений равно числу различных перестановок из n символов, т.е. равно n!. Знак произведения (4.4) равен (- 1)q, где q – число инверсий в перестановке вторых индексов элементов.
Определителем n -го порядка, соответствующим матрице (4.3), называется алгебраическая сумма n! членов вида (4.4). Для записи определителя употребляется символ или detA = (детерминант, или определитель, матрицы А).
Свойства определителей
1. Определитель не меняется при транспонировании.
2. Если одна из строк определителя состоит из нулей, то определитель равен нулю.
3. Если в определителе переставить две строки, определитель поменяет знак.
4. Определитель, содержащий две одинаковые строки, равен нулю.
5. Если все элементы некоторой строки определителя умножить на некоторое число k, то сам определитель умножится на k.
6. Определитель, содержащий две пропорциональные строки, равен нулю.
7. Если все элементы i-й строки определителя представлены в виде суммы двух слагаемых ai j = bj + cj (j = 1,…,n), то определитель равен сумме определителей, у которых все строки, кроме i-ой, – такие же, как в заданном определителе, а i-я строка в одном из слагаемых состоит из элементов bj, в другом – из элементов cj.
8. Определитель не меняется, если к элементам одной из его строк прибавляются соответствующие элементы другой строки, умноженные на одно и то же число.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Минором Mi j элемента ai j определителя d n-го порядка называется определитель порядка n-1, который получается из d вычеркиванием строки и столбца, содержащих данный элемент.
Алгебраическим дополнением элемента ai j определителя d называется его минор Mi j, взятый со знаком (-1) i + j. Алгебраическое дополнение элемента ai j будем обозначать Ai j. Таким образом, Ai j = (-1) i + j Mi j.
Способы практического вычисления определителей, основанные на том, что определитель порядка n может быть выражен через определители более низких порядков, дает следующая теорема.
Теорема (разложение определителя по строке или столбцу).
Определитель равен сумме произведений всех элементов произвольной его строки (или столбца) на их алгебраические дополнения. Иначе говоря, имеет место разложение d по элементам i-й строки
d = ai 1 Ai 1 + ai 2 Ai 2 +… + ai n Ai n (i = 1,…,n)
или j- го столбца
d = a1 j A1 j + a2 j A2 j +… + an j An j (j =1,…,n ).
В частности, если все элементы строки (или столбца), кроме одного, равны нулю, то определитель равен этому элементу, умноженному на его алгебраическое дополнение.
Формула вычисления определителя третьего порядка.
Для облегчения запоминания этой формулы:
Пример 2.4. Не вычисляя определителя , показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель , равный исходному. Если из третьей строки также вычесть первую, то получится определитель , в котором две строки пропорциональны. Такой определитель равен нулю.
Пример 2.5. Вычислить определитель D = , разложив его по элементам второго столбца.
Решение. Разложим определитель по элементам второго столбца:
D = a12A12 + a22A22+a32A32=
.
Пример 2.6. Вычислить определитель
,
в котором все элементы по одну сторону от главной диагонали равны нулю.
Решение. Разложим определитель А по первой строке:
.
Определитель, стоящий справа, можно снова разложить по первой строке, тогда получим:
.
И так далее. После n шагов придем к равенству A = а11 а22… ann.
Пример 2.7. Вычислить определитель .
Решение. Если к каждой строке определителя, начиная со второй, прибавить первую строку, то получится определитель, в котором все элементы, находящиеся ниже главной диагонали, будут равны нулю. А именно, получим определитель: , равный исходному.
Рассуждая, как в предыдущем примере найдем, что он равен произведению элементов главной диагонали, т.е. n!. Способ, с помощью которого вычислен данный определитель, называется способом приведения к треугольному виду.
Источник
На главную страницу
Определители
В конец страницы
3. 1.
ОПРЕДЕЛИТЕЛИ
Каждой квадратной матрице А соответствует число, которое называется ее
определителем, или детерминантом, и обозначается |А|,
det
А,
или .
Определителем, или детерминантом, n-го порядка служит число, записываемое
в виде квадратной таблицы
det
А
и равное алгебраической
сумме
n!
произведений вида .
Итак,
det
А,
где суммирование
распространено на все перестановки из чисел 1, 2, …,
n.
Здесь –
число инверсий в перестановке .
Говорят, что числа и
образуют
инверсию в перестановке ,
если большее из чисел и
расположено
левее меньшего.
Например, для
n
2
,
для
n
3
Правило вычисления
определителя равносильно
правилу треугольников (правилу Саррюса), которое схематически можно записать как
ОСНОВНЫЕ СВОЙСТВА
ОПРЕДЕЛИТЕЛЯ
1. Равноправие строк и столбцов.
При транспонировании матрицыее определитель не меняется.
2. Если все элементы какого-либо столбца (строки) определителя равны
нулю, то определитель также равен нулю. Это свойство очевидно, так как каждое
слагаемое содержит по одному и только одному сомножителю из каждого столбца
(строки).
3. Антисимметрия.
При перестановке двух любых столбцов (строк) определителя его знак меняется на
противоположный, а абсолютная величина остается неизменной.
Доказательство свойств 1 и 3
основано на правиле расстановки знаков членов определителя.
4. Определитель с
двумя одинаковыми столбцами (строками) равен нулю.
Действительно, при
перестановке, например, двух одинаковых столбцов определитель не изменяется, но
вместе с тем он в силу третьего свойства меняет знак на обратный, т. е.
,
откуда или
.
5. Линейность.
Если j-й
столбец
(i-я
строка
A)
определителя det
A
является линейной комбинацией
A λB
+
μC
(A λB
+
μC)
двух произвольных столбцов (строк) В и С , то и сам определитель
оказывается линейной комбинацией
det
A
det
A(λB+
μC)
λdet
A(B)
+ μdet
A(C)
определителей det
A(B)
и det
A(C).
Здесь det
A(B)
(det
A(C))
– определитель, полученный из определителя
det
А заменой
в нем j-го
столбца
A на
столбец В(столбец С ).
6. Общий множитель
всех элементов какого-либо столбца (строки) определителя можно вынести за его
знак. Отсюда следует, что если какой-либо столбец (строку) определителя умножить
на число λ, то сам определитель умножится на это число.
7. Если какой-либо
столбец (строка) определителя является линейной комбинацией других его столбцов
(строк), то определитель равен нулю.
Свойства 6 и 7 вытекают из
пятого свойства.
8. Определитель не
изменится, если к любому его столбцу (строке) прибавить произвольную линейную
комбинацию его столбцов (строк).
Действительно, в силу
линейности определитель равен сумме исходного определителя и определителя с
двумя одинаковыми столбцами (строками).
9. Определитель суммы
двух квадратных матриц одного и того же порядка
n
A
и В ,
i,
j
= равен
сумме всех различных определителей порядка
n,
которые могут получиться, если часть строк (столбцов) брать совпадающими с
соответствующими строками (столбцами) матрицы А, а оставшуюся часть –
совпадающими с соответствующими строками (столбцами) матрицы В.
Доказательство следует из
свойства линейности определителя.
10. Определитель
произведения двух матриц равен произведению их определителей
det
(AВ)
det
A×det
B.
Назад
К началу страницы
Вперед
Источник
Определение 9. Транспонированием A матрицы называется такое ее преобразование, при котором строки матрицы становятся ее столбцами с теми же самыми номерами.
Матрица транспонированная матрице A обозначается символом :
.
Свойство 1. Определитель транспонированной матрицы равен определителю исходной матрицы, т. е. .
Доказательство. ОПределителя матрицы А есть алгебраическая сумма N! произведений вида
(11)
Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца матрицы A, со знаком равным знаку подстановки
.
Так как сомножители произведения (11) также находятся по одному в каждом столбце и каждой строке матрицы , то каждое произведение определителя матрицы A входит в определитель матрицы . Отсюда. так как количество слагаемых в и в одинаково, следует, что и в состоят из одних и тех же слагаемых. Для того, чтобы показать, что знаки произведений равны, составим подстановку для произведения (11) в (учитываем, что строки матрицы А стали столбцами матрицы с теми же номерами). Она равна подтановке:
.
Подстановки иИмеют одинаковое число инверсий, четность и знак.
Таким образом и суммы одних и тех же произведений и поэтому . Свойство доказано.
Замечание 1. Из свойства 1 вытекает, что строки и столбцы матрицы Равноправны, т. е., если какое-нибудь свойство доказано для строк, то оно будет справедливо и для столбцов и обратно. Поэтому дальнейшие свойства формулируются и доказываются только для строк. В дальнейшем под строками и столбцами определителя понимаются строки и столбцы соответствующей матрицы.
Свойство 2. Если в матрице поменять местами две строки, то абсолютная величина определителя не меняется, а знак определителя меняется на противоположный.
Доказательство. Пусть даны исходный и преобразованный определитель:
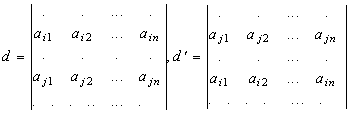. (12)
Определитель Получается из определителя D перестановкой I-й и J-й строк (точками обозначены все остальные строки, которые в D и Совпадают. Требуется доказать, что D= -.
ОПределитель D есть алгебраическая сумма N! произведений вида
, (13)
Где в каждое произведение входит по одному элементу из каждой строки и каждого столбца определителя D, со знаком равным знаку подстановки
.
Так как сомножители произведения (13) также находятся по одному в каждом столбце и каждой строке определителя , то каждое произведение определителя D входит в определитель . Отсюда, так как количество слагаемых в D и одинаково, следует, что D и состоят из одних и тех же произведений, Для того, чтобы показать, что D= –, достаточно показать, что каждое произведение (13) определителях D и Имеет противоположные знаки. Знак произведения (13) в определителе равен знаку подстановки:
(учитываем, что элемент Лежит в определителе в J-й строке в-м столбце, элемент – в I-й строке и в -м столбце). У подстановок и Совпадают вторые строки, а первая строка подстановки Получена из первой строки подстановки транспозицией элементов I и J . Поэтому в силу теоремы 2 подстановки и Имеют противоположную четность и знак. Отсюда образом произведение (13) входит в определители D и с противоположным знаком. Таким образом определители D и суммы одних и тех же произведений, но с противоположными знаками и D= –. . Свойство доказано.
Свойство 3. Если в определителе есть две одинаковые строки, то определитель равен нулю.
Доказательство. Пусть в определителе D I-я строка равна j-й строке. Переставим I-ю и J-ю строки местами и получим определитель (см.(13)). По свойству 2 D= –. Так как I-я и J-я строки равны, то D= . Из этих равенств находим, что D= 0. Свойство доказано.
Свойство 4. Если в определителе есть нулевая строка, то определитель равен нулю.
Доказательство. Пусть в определителе I-я строка нулевая. По определению определителя он равен алгебраической сумме произведений вида:
.
В каждое произведение входит нулевой элемент I-й строки и поэтому оно равно нулю. Следовательно, и определитель равен нулю. Свойство доказано.
Свойство 5. Если все элементы какой-нибудь строки определителя представлены в виде двух слагаемых, то определитель равен сумме двух определителей, в первом из которых элементы отмеченной строки равны соответствующим первым слагаемым, во втором – вторым слагаемым.
Пусть все элементы I-й строки представлены в виде ; J=1,2,…,N. Тогда свойство перепишется в виде:
=
= .
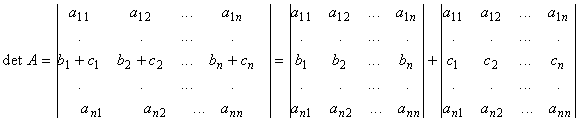Доказательство. По формуле (8) находим
= .
Свойство доказано.
Замечание 2. Индукцией по m легко доказать, что свойство 5 справедливо для случая, когда каждый элемент i-й строки сумма m слагаемых, .
Свойство 6. Если все элементы какой-нибудь строки определителя имеют общий множитель, то его можно вынести за знак определителя, т. е., если элементы какой-нибудь строки определителя умножить на число k, то и сам определитель умножится на число k.
.
Доказательство. По формуле (8) находим
Свойство доказано.
Свойство 7. Если в определителе есть две пропорциональны строки, то он равен нулю.
Доказательство. Пусть I-я и J-я строки определителя пропорциональны, т. е. . Вынося из J-й общий множитель K за знак определителя, получим определитель с двумя равными строками, который равен нулю. Поэтому и исходный определитель равен нулю. Свойство доказано.
Свойство 8. Если к какой-нибудь строке определителя прибавить другую строку, умноженную на число k, то определитель от этого не изменится.
Доказательство. Пусть к I-й строке определителя прибавили ее J-ю строку, умноженную на число K . Тогда по свойствам 5 и 7 получаем:
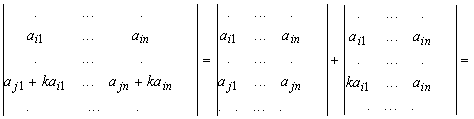
Свойство доказано.
Определение 10. Говорят, что I-я строка матрицы A есть линейная комбинация остальных строк определителя, если существуют такие числа , что каждый элемент I-й строки есть сумма попарных произведений этих чисел на соответствующие элементы остальных строк матрицы, т. е.
Свойство 9. Если какая-нибудь строка определителя есть линейная комбинация остальных строк определителя, то определитель равен нулю.
Доказательство. Если I-я строка определителя есть линейная комбинация остальных строк определителя, то по замечанию 2 определитель равен сумме n-1 определителей с пропорциональными строками, и по свойству 7 все такие определители равны нулю. Тогда и исходный определитель равен нулю. Свойство доказано.
Источник