Какие из перечисленных свойств площадей является основными

1. Ответ

   Ответ дан
   емнмкгднакснр

   А) площадь квадрата равна квадрата своей стороны .

Не тот ответ, который вам нужен?

Найди нужный

Самые новые вопросы

План-конспект урока по теме «Решение задач с использованием свойств площадей»

Цель: развитие умений в применение знаний на практике; развивать мышление, внимание и память;

воспитывать умение контролировать себя и не бояться ошибаться;

научиться находить различные пути поиска решения задач с использованием свойств площадей.

С – 1 С – 2

С – 3 С – 4

С – 5 С – 6

С – 7 С – 8

Рис. 2.

Ход урока

1. Организационный момент.

2. Сообщение темы урока

Учитель: Сегодня мы на уроке будем решать задачи, свойства площадей.

Двух учеников приглашают к доске.

1. 1. Запишите на доске все формулы площади треугольника.

   2. Запишите на доске формулы площади трапеции.

Ответы

1).

2)

3) ,

где

4)

5) ,

r – радиус вписанной в треугольник окружности

6)

II. 1).

2) , где MN – средняя линия трапеции

3) ,

где d1, d2 – диагонали трапеции, α – угол между ними

4) ,

где с – боковая сторона трапеции, h –перпендикуляр из середины другой боковой стороны на первую или её продолжение

Пока ученики записывают формулы, спросить учеников с мест правила «Свойства площадей».

Ответ

1). Каждая фигура имеет положительную площадь.

2). Площадь квадрата со стороной равной единице длины равна единице площади.

3). Если фигура разбивается на две части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.

Рассмотрите площади треугольника, написанные на доске.

Вопрос. Какая из формул является основной?

Ответ. .

Назовите следствия из этой формулы, используя таблицу «Свойства площадей».

С–1. Если вершину треугольника передвигать по прямой, параллельной основанию, то площадь при этом не изменится.

С–2. Если два треугольника имеют одинаковые высоты, то отношение их площадей равно отношению длин оснований (сторон, на которые опущены эти высоты).

С–3. Если два треугольника имеют общий угол, то их площади относятся как произведение сторон, заключающих этот угол.

С–4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

С–5. Медиана треугольника делит его на 2 равновеликие части.

С–6. Медианы треугольника делят его на три равновеликие части.

С–7. Медианы треугольника делят его на 6 равновеликих частей.

С–8. Средняя линия треугольника площади отсекает от него треугольник площади .

Решение задач

Задача 1. Дано – трапеция, и – диагонали. Пересекающиеся диагонали разбивают трапецию на 4 треугольника с вершиной в точке О. и – треугольники, которые прилегают к основаниям и треугольники и – треугольники, которые прилегают к боковым сторонам. Обозначим , , , , .

Найдите связь между площадями треугольника.

Рис. 2.2

Выразите площадь трапеции через и , т. е. через площади треугольников, прилегающих к основаниям трапеции.

Так как , то надо выразить и через и .

Вопрос. Что можно сказать про площади и ?

Ответ. =, т. к. треугольники и имеют одинаковые площади, а если от равных отнять площадь , то получим равные площади и .

Выразите через и . , .

Докажите, что и .

(2.1)

(2.2)

Перемножив (2.1) и (2.2), получим

.

.

Вопрос. Как сформулировать правило, которое мы вывели?

Ответ. Площадь треугольника, прилегающего к боковой стороне трапеции есть среднее геометрическое между площадями треугольников, прилегающих к основаниям трапеции.

Вопрос. Как вывести соотношение , используя свойства площадей?

Ответ. .

Вопрос. Какое свойство площадей здесь использовались?

Ответ. С – 3, С – 2 (ученики отвечают устно).

Вопрос. Как можно ещё вывести соотношения ?

Ответ. .

; .

Найдите площадь трапеции (рис. 3)

Рис. 3

или .

Таким соотношением связана площадь трапеции с площадями треугольников, прилегающих к её основаниям. Итак, для трапеции

.

Вопрос. Справедливо ли это соотношение для любого четырёхугольника?

Ответ. Нет, т. к. .

Основания у треугольников и одинаковые (рис. 2.4), но их вершины не на параллельных прямых.

Рис. 2.4

Вопрос. А какое соотношение между можно вывести для четырёхугольника (рис. 2.4)?

Ответ. ,

т. е. произведения площадей треугольников, прилегающих к противоположным сторонам четырёхугольника равны.

Задача 2. (обратная).

Дано: выпуклый четырёхугольник

Докажите, что этот четырёхугольник есть трапеция.

Доказательство.

С другой стороны, (рис. 2.4). , следовательно , но , (рис. 2.4), следовательно , следовательно , следовательно , следовательно и , т. е. , а это означает, что , т. е. четырёхугольник – трапеция.

Задача 3. Через некоторую точку, взятую внутри треугольника проведены 3 прямые, соответственно параллельные сторонам треугольника. Эти прямые разделяют треугольник на 6 частей, из которых три треугольника с площадями . Найдите площадь треугольника.

Рис. 2.5

Дано: . . . . , , .

Найдите .

Решение.

1)  , следовательно 9площади подобных треугольников относятся как квадрат коэффициента подобия).

2) ;.

.

, отсюда .

Итог урока

Повесить таблицу «Итог урока» (сделать из достаточно плотной бумаги, с магнитами на обратной стороне, прикрепляется мгновенно на обратную доску).

Вопрос. Мысленно вернитесь ко всем задачам, которые были рассмотрены на уроке. Попытайтесь вспомнить из всех свойств площадей, какие свойства мы применяли на уроке.

Ответ. 1) Равные фигуры имеют одинаковые площади.

2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.

3) Если от равных отнять равные, то получим равные.

Вопрос. Какие следствия из формулы мы применяли?

Ответ. С – 1, С – 2, С – 3, С – 4, С – 5 все следствия ученики рассказывают.

Вопрос. Из множества формул для нахождения площади простых фигур какие бы вы использовали?

Ответ. ;.

Задание на дом

1. Диагонали делят трапецию на 4 треугольника. Площади двух из них равны 1 см2 и 2 см2. Какой может быть площадь трапеции?

2. Точки – середины сторон выпуклых четырёхугольников и . Докажите, что .

3. Дано: ; – середины сторон соответственно. пересекает в точке . Докажите, что (задача автора).

4. В параллелограмме точки и делят диагональ на три равные части. Точки и – середины сторон и . Найдите отношение площади четырёхугольника к площади параллелограмма (задача автора, дополнительное задание).

Домашнее задание выдаётся каждому ученику на листке.

Измерение площадей

Для измерения площадей используют такие единицы измерения:

квадратный сантиметр, квадратный дециметр, квадратный метр, квадратный километр

Вспомните, что квадрат – это прямоугольник, у которого все стороны равны

Квадратный сантиметр – это площадь квадрата со стороной в 1 см    

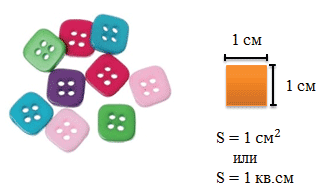
Квадратный дециметр – это площадь квадрата со стороной в 1 дм

Квадратный метр – это площадь квадрата со стороной в 1 м

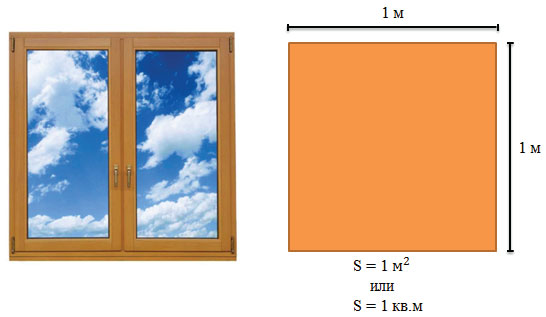
Для измерения больших площадей используют квадратный километр – это площадь квадрата, сторона которого равна 1 км

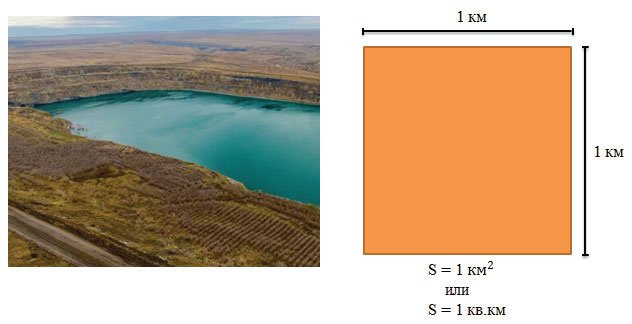
Слова «квадратный километр» сокращенно при числе записывают так – 1 км2, 2 км2, 130 км2.

В квадратных километрах измеряют, например, площади городов (площадь Москвы 1091 км2)

Обозначают площадь заглавной буквой латинского алфавита S

Площади полей измеряют в гектарах (га).

Гектар – это площадь квадрата со стороной 100 м.

Значит, 1 га равен 100 ∙ 100 квадратных метров, то    есть 1 га = 10 000 м2.

Площади небольших участков земли измеряют в арах (а).

Ар (сотка) – площадь квадрата со стороной 10 м.

Значит, 1 а  =  100 м2.

Так как 1 дм = 10 см, то в 1 дм2 содержится 10 · 10 квадратных сантиметров, то есть 1 дм2 = 100 см2.

Так же устанавливаем, что 1 м2 = 100 дм2.

Так как 1 м = 100 см, то в 1 м2 содержится 100 ∙  100 квадратных сантиметров, то есть 1 м2 = 10 000 см2.

Измерить площадь – значит подсчитать, сколько единичных квадратов в ней помещается.

Соотношения между единицами измерения площадей 

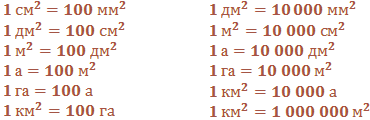
Если длина и ширина прямоугольника выражены, например, в метрах, то его площадь выражается в квадратных метрах.

Если длина и ширина прямоугольника измерены в разных единицах, то их надо выразить в одних единицах.

Свойства площадей

1. Равные фигуры имеют равные площади (равные фигуры при наложении совпадут).
2. Площадь фигуры равна сумме площадей фигур, из которых она состоит.