Какие есть свойства сложения и вычитания

Умножение, сложение, вычитание и деление – основные операции с целыми числами. Результаты этих операций с любыми целыми числами обладают рядом характеристик. Иначе говоря, операции умножения, сложения, вычитания и деления целых чисел обладают свойствами. Данная статья посвящена рассмотрению основных свойств умножения, сложения, вычитания и деления целых чисел.
Сложение целых чисел. Основные свойства
Все свойства сложения натуральных чисел оказываются справедливы и для целых чисел. Ведь множество целых чисел ℤ включает в себя множество натуральных чисел ℕ. Приведем ниже основные свойства сложения.
Коммутативное свойство сложения
Переместительное (коммутативное свойство) или переместительный закон.
От перемены мест слагаемых сумма не меняется.
a+b=b+a
Согласно этому свойству, справедливо равенство:
35+251=251+35
Свойство коммутативности работает вне зависимости от знака.
-528+3700=3700+-528
Ассоциативное свойство сложения
Сочетательное (ассоциативное свойство) или сочетательный закон.
Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.
a+b+c=a+b+c
Примечание: данное свойство применимо и для большего количества слагаемых.
Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:
64+81+(-49)=64+81+(-49)=64+81+(-49);
(128+(-75))+96=128+((-75)+96).
Свойства сложения, связанные с числом 0
1. Число нуль – нейтральный по сложению элемент.
Прибавление нуля к любому целому числу не меняет этого числа.
a+0=a
2. Сумма любого целого числа и противоположного ему числа равна нулю.
a+(-a)=0
Умножение целых чисел. Основные свойства
Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.
Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.
Переместительное свойство умножения
От перемены мест множителей произведение не меняется.
a·b=b·a
Приведем пример. Очевидно, что произведение целых чисел 2·3 эквивалентно произведению 3·2.
Сочетательное свойство умножения
Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:
a·(b·c)=(a·b)·c
a, b, c – произвольные целые числа.
Примечание: данное свойство применимо и для большего количества множителей.
В соответствии с этим свойством можно говорить о справедливости следующих равенств:
-12·3·8=-12·3·8;
119·((-251)·36)=(119·(-251))·36.
Умножение числа на нуль
Результатом умножения любого целого числа на нуль является число нуль.
a·0=0
Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.
a·b=0 если a=0 или b=0.
Умножение числа на единицу
Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.
a·1=a
Распределительное свойство умножения относительно суммы.
Произведение целого числа a на сумму двух чисел b и c равно сумме произведений a·b и a·c.
a·(b+c)=a·b+a·c
Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.
В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.
Вычитание целых чисел. Основные свойства
Вычитание – действие, обратное сложению. Число c является разностью двух чисел a и b тогда, когда сумма b+c равна a. Можно сказать, что разность чисел a и b – это сумма чисел a и -b. Свойства вычитания являются следствием свойств сложения и умножения.
Основные свойства вычитания
- Вычитание чисел не обладает переместительным свойством за исключением случая, когда a=b. a-b≠b-a.
- Разность целых чисел, равных друг другу: a-a=0.
- Вычитание суммы двух чисел из другого числа: a-(b+c)=a-b-c.
- Вычитание целого числа из суммы: a+b-c=a-c+b=a+(b-c).
- Распределительное свойство умножения относительно вычитания: a·(b-c)=a·b-a·c.
Деление целых чисел. Основные свойства
Деление – операция, обратная умножению. Число c называется частным от деления чисел a и b, когда произведение b·c равно a. Запишем основные свойства деления целых чисел.
Основные свойства деления
- Деление на нуль невозможно.
- Деление нуля на число: 0a=0.
- Деление равных чисел: aa=1.
- Деление на единицу: a1=a.
- Для деления переместительное свойства не выполняется: ab≠ba.
- Деление суммы и разности на число: a±bc=ac±bc.
- Деление произведения на число: a·bc=ac·b, если a делится на c; a·bc=a·bс, если b делится на c; a·bc=a·bс=ac·b, если a и b делятся на c.
- Деление числа на произведение: ab·c=ab·1c=ac·1b.
Источник
Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
Источник
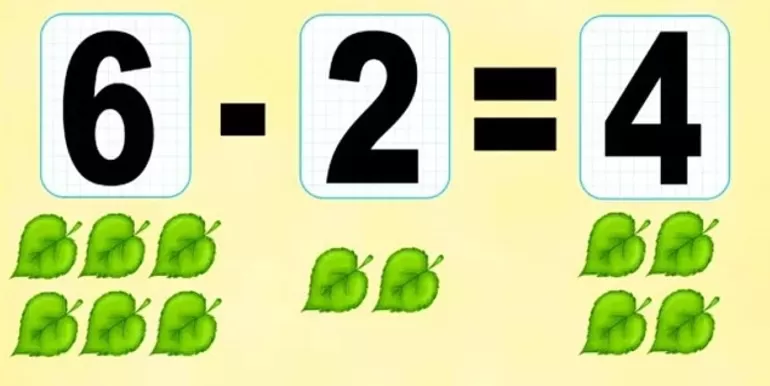
Понятие действия
Вычитание — бинарная операция, результатом выполнения которой является число, называемое разностью. В действии участвуют два аргумента: один из них — уменьшаемое, а другой — вычитаемое. Ответ получается путем уменьшения значения одного аргумента на второй. Уменьшаемое располагается слева, а вычитаемое — справа. Обозначают операцию знаком минус, который ставят между двумя числами. По сути, уменьшение — это действие, обратное сложению.
При операции вычитания используют три термина:
- Разность — ответ, полученный после выполнения действия.
- Уменьшаемое — часть выражения, которое нужно уменьшить.
- Вычитаемое — определяет величину уменьшения.
Стоит отметить, что результат вычитания может быть как положительным, так и отрицательным. Рассмотреть процесс уменьшения удобно на примере:
Пусть в вазе лежит восемь яблок. Если три штуки забрать, то в вазе останется пять.
Математическая запись такого действия будет выглядеть как 8 — 3 = 5. В ней число восемь является уменьшаемым, три — вычитаемым, а пять — разностью (результатом). Произносится эта запись так: разность восьми и трёх равняется пяти.
Применение вычитание также позволяет сравнивать два числа. Пытаясь вычислить, какое число больше, а какое меньше, фактически определяют ту часть выражения, где находится больше единиц. Найти же, какое число больше или меньше другого, можно как раз вычитанием. Например для того чтобы узнать, насколько 50 меньше 80, нужно из последнего вычесть первое: 80 — 50 = 30. То есть второе число больше первого на тридцать единиц.
Так как уменьшение — это операция, обратная суммированию (прибавлению), то проверкой вычитания будет сумма. Пусть дано равенство: 66 — 13 = 43. Чтобы проверить его верность, можно к тринадцати (вычитаемому) прибавить разность (ответ). В результате должно получиться число, равное уменьшаемому. Для рассматриваемого примера проверка выглядит следующим образом: 13 + 43 = 66. Осуществить проверку можно и другим способом. Для этого необходимо уменьшаемое уменьшить на разность. Если после действия ответ совпадет с вычитаемым, то задание решено верно: 66 — 43 = 13.
Уменьшение многозначных чисел обычно выполняют в столбик. Для этого друг под другом пишут уменьшаемое и вычитаемое таким образом, чтобы разряды чисел находились строго один под одним. Затем проводят черту и, начиная с наименьшего разряда, выполняют минусование. Результат записывают под чертой.
Свойства уменьшения
Основная формула вычитания имеет следующий вид: a — b = c. При этом справедливыми будут утверждения: с + b = a и a — c = b. Числа, подставляемые в формулу, могут быть любыми, например натуральными, дробными, рациональными. Но вычитать можно только те аргументы, которые принадлежат одному множеству, то есть относятся к одному типу. Действие характеризуется несколькими важными свойствами:

- Вычитание нулевого элемента не изменит уменьшаемое. Если же уменьшается ноль, то в ответе получится вычитаемое с отрицательным знаком. Таким образом, при вычитании некого числа аргумент уменьшается на определенное число единиц. Если же из уменьшаемого отнять такое же число, то результатом будет ноль. Математические записи, описывающие эти свойства, следующие: a — 0 = a; a — a = 0; 0 — a = -a.
- При вычитании суммы из числа можно сначала вычесть из этого числа слагаемое, а затем из полученного результата отнять второе слагаемое: a — (b + c) = a — b — c. Аналогично можно поступить и для вычитания числа из суммы: (a + b) — c = (a — c) + b = a + (b — c).
- Чтобы сложить разность и число, можно прибавить уменьшаемое, а уже и из рассчитанной суммы вычесть вычитаемое: а + (b — c) = a + b — c.
Кроме этого, действие характеризуется антикоммутативностью — правило позволяет поменять аргументы местами, но при этом перед действием необходимо поставить знак минус, и дистрибутивностью — сочетанием умножения и вычитания. Других правил не бывает.
Если рассмотреть процесс на графике, то можно говорить, что происходит перенос числа по числовой прямой в левую часть. Следует отметить, что если действие выполняется с отрицательным числом, то получится операция сложения, так как минус на минус будет давать плюс. В этом случае результат сместится в правую часть. Важным является и то, что при вычитании переместительный закон, как для сложения или умножения, выполняться не будет. Действительно, очевидно, что 4 — 2 не будет равняться 2 — 4.
Этим базисным понятиям арифметики начинают обучать в 5 классе. Правила и свойства сложения и вычитания помогают довольно сильно облегчить ту или иную задачу. Так, чтобы вычесть сумму чисел из натурального аргумента, можно сначала найти сумму, а потом выполнить вычитание. Но, используя правило, может быть и удобнее сначала выполнить уменьшение, а потом разность прибавить к числу. Например, 38 — (28 + 7). Здесь проще сначала от тридцати восьми отнять двадцать восемь, а потом прибавить семь, чем сначала выполнять действие в скобках.
Простые примеры
Знание правил должно быть обязательно подкреплено практическим навыком. Поэтому как в школе, так и в видеоуроках после прослушивания лекции учащимся предлагается решить несколько примеров. Вначале школьники делают вычисления совместно с преподавателем, который должен рассказать, как лучше поступить в том или ином задании. Затем уже ученикам нужно попробовать самостоятельно порешать примеры. Для этого используют математические тренажеры.
Вот один из них, состоящий из 15 тестов и затрагивающий различные правила:
- 2 — 1 = 1;
- 35 — 5 = 30;
- 100 — 41 = 59;
- 700 — 545 = 155;
- 1 + 1 — 2 = 0 = 2 — 2 = 0;
- 345 — 0 = 345;
- 0 — 15 = -15;
- 12275 — 12275 = 0;
- 32 + 0 — 1 = 32 — 1 = 31;
- 139 — (10 + 39) = 139 — 39 + 10 = 100 + 10 = 110;
- (123 + 17) — 33 = (123 — 33) + 17 = 90 +17 = 107;
- (201 — 11 + 1379) — 1379 = (201 — 11) + (1379 — 1379) = 190 + 0 = 190;
- 545 — (402 — 35) = 545 + 402 — 35 = 545 — 35 — 402 = 510 — 402 = 108;
- 32 — 76 + 96 — 76 — 32 = (32 — 32) — (76 — 76) + 96 = 96;
- 3 — 6 — 50 + 2 + 1 = (3 + 2 + 1) — 6 — 50 = 6 — 6 — 50 = 0 — 50 = -50.
Только с опытом можно понять, в каких случаях желательно использовать переместительное правило, а в каких удобнее применить сочетательный закон без изменения записи.

Пример. Пусть у Ирины Петровны на кредитной карте находилось 3282 рубля. В конце месяца ей на эту карту начислили 6018 рублей пенсии. Ирина Петровна в магазине купила себе пирог и рассчиталась картой. Стоимость покупки составила 318 рублей. Спрашивается, сколько денег осталось у пенсионерки на счету. Эту задачу можно решить тремя разными способами. Какой из них удобнее, зависит от личного предпочтения:
- (3282 + 6018) — 318 = 9300 — 318 = 8982.
- 3282 — 318 + 6018 = 2964 + 6018 = 8982.
- 6018 — 318 + 3282 = 5700 + 3282 = 8982.
Таким образом, какой бы способ ни был выбран, можно утверждать, что у Ирины Петровны на карте после покупки останется 8982 рубля. После окончания 5 класса законы вычитания нужно знать так же хорошо, как и таблицу умножения. Только в этом случае от арифметики можно будет переходить к изучению алгебры.
Вычитание на числовой прямой
Довольно наглядно свойства вычитания можно увидеть на иллюстрации, изобразив действие на числовой прямой. На ней нужно отложить точки через равный промежуток, например от ноля до десяти, и последовательно их пронумеровать.
Так, для решения примера 3 + 5 — 2 на прямой необходимо найти цифру три. Согласно условию и свойствам уменьшения, из неё можно вычесть двойку. Следовательно, нужно влево от тройки отсчитать два пункта. На иллюстрации этому будет соответствовать точка один. Затем по условию задания нужно прибавить пять единиц. На графике этому будет соответствовать перемещение на пять точек вправо. Итогом всех действий получится точка, подписанная как шесть.
Аналогичным образом можно подсчитать любое вычитание или сложение. Но этот метод хорош для обучения при значениях не больше десяти. Очень наглядно иллюстрация показывает и вычитание ноля. Так как при уменьшении на ноль передвигаться по прямой не нужно, то после вычитания значение уменьшаемого не изменяется.

Задача 1. Пусть имеется отрезок АБ. Нужно определить его длину, если известно, что первой точке (А) соответствует число минус пять, а второй (Б) — девять. На прямой нужно отложить ноль и по обе стороны от него отметить точку, соответствующую минус пяти и девяти. Согласно условию, задачу можно записать как -5 + АБ = 9.

Отсюда следует, что АБ = 9 — (- 5). Сформулировав в уме правило, что минус на минус даёт плюс, равенство верно будет переписать как АБ = 9 + 5 = 14. Проверку можно выполнить, уменьшив результат на пять: АБ — 5 = 9. А можно на графике отсчитать в правую сторону четырнадцать отрезков. Последний из них должен будет совпадать с числом -5.
Задача 2. Велосипедист за день преодолел путь от села Крюково до деревни Морозко. Вычислить, какое он преодолел расстояние за первый час, если за следующее время он проехал 13 км. Для иллюстрации условия задачи нужно на прямой изобразить точку отсчёта, обозначив её за ноль. Затем отметить конечную точку, соответствующую 18 км (в удобном масштабе).
На прямой от конечной точки отсчитать 13. Теперь от тринадцати подсчитать количество отрезков до начальной точки. Математические же вычисления будут выглядеть так: 18 — 13 = 4 км. И в первом, и во втором случае ответ будет аналогичным.
Источник
