Какие бывают свойства умножения и деления

- Главная
- Справочники
- Справочник по математике для начальной школы
- Умножение
- Свойства умножения
1) Переместительное свойство: от перестановки множителей произведение не изменится.
3 • 4 = 12
4 • 3 = 12
Значит, 3 • 4 = 4 • 3
2) Сочетательное свойство: два соседних множителя можно заменить их произведением.
(6 • 2) • 5 = 6 • (2 • 5)
3) Распределительное свойство: при умножении суммы на число можно умножить на него каждое слагаемое в отдельности и полученные результаты сложить.
(3 + 10) • 7 = 3 • 7 + 10 • 7 = 91.
4) Чтобы умножить сумму на число, можно сначала выполнить сложение и полученный результат умножить на число:
(3 + 10) • 7 = 13 • 7 = 91.
5) Чтобы умножить число на произведение, можно сначала выполнить умножение в скобках, а затем умножить число на полученный результат:
4 • (3 • 5) = 4 • 15 = 60.
6) Чтобы умножить число на сумму, можно сначала выполнить сложение, а затем умножить число на полученный результат:
2 • (3 + 5) = 2 • 8 = 16
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Табличное умножение
Внетабличное умножение
Умножение суммы на число
Умножение на однозначное число в столбик
Умножение на числа, оканчивающиеся нулями
Умножение
Правило встречается в следующих упражнениях:
3 класс
Страница 46. Вариант 1. Проверочная работа 1,
Моро, Волкова, Проверочные работы
Страница 47. Вариант 2. Проверочная работа 1,
Моро, Волкова, Проверочные работы
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 91,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 101,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 105,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 106,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
4 класс
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 24,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 35,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 54,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 93,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 24,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 38,
Моро, Волкова, Рабочая тетрадь, часть 2
Страница 42,
Моро, Волкова, Рабочая тетрадь, часть 2
Источник
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a – b) = m · a – m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a – b) · m = a · m – b · m.
Переход от умножения:
m · (a + b) и m · (a – b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a – m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a – m · b
к умножению:
m · (a + b) и m · (a – b)
называется вынесением общего множителя за скобки.
Источник
Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
Источник
- Деление произведения на число
- Деление числа на произведение
- Деление суммы на число
- Деление разности на число
- Общие формулы свойств деления
Деление произведения на число
Произведение можно разделить на число двумя способами:
1) Чтобы разделить произведение на какое-нибудь число, можно сначала вычислить значение произведения (выполнить умножение) и полученный результат разделить.
Например, чтобы найти значение выражения:
(12 · 5) : 3,
можно сначала умножить 12 на 5:
12 · 5 = 60
и полученное произведение разделить на 3:
60 : 3 = 20,
значит (12 · 5) : 3 = 60 : 3 = 20.
Если один из сомножителей делится на число, на которое надо разделить произведение, то можно воспользоваться вторым способом нахождения частного от деления произведения на число.
2) Чтобы разделить произведение на какое-нибудь число, можно разделить на это число один любой сомножитель, оставив другие без изменений.
Например, чтобы найти значение выражения:
(8 · 20) : 4,
можно сначала разделить любой из сомножителей (8 или 20) на 4:
8 : 4 = 2
и полученное частное умножить на другой сомножитель:
2 · 20 = 40,
значит (8 · 20) : 4 = (8 : 4) · 20 = 2 · 20 = 40.
Данное выражение можно решить ещё так:
(8 · 20) : 4 = 8 · (20 : 4) = 8 · 5 = 40.
Деление числа на произведение
Число можно разделить на произведение двумя способами:
1) Чтобы разделить какое-нибудь число на произведение, можно сначала вычислить значение произведения (выполнить умножение), а затем разделить число на полученный результат.
Например, чтобы найти значение выражения:
60 : (3 · 2),
можно сначала умножить 3 на 2:
3 · 2 = 6
и разделить 60 на полученный результат:
60 : 6 = 10,
значит 60 : (3 · 2) = 60 : 6 = 10.
Если число, которое нужно разделить на произведение, делится на каждый сомножитель, из которого состоит данное произведение, то можно воспользоваться вторым способом нахождения частного от деления числа на произведение.
2) Чтобы разделить какое-нибудь число на произведение, можно разделить это число на первый сомножитель, полученное частное разделить на второй сомножитель, это частное на третий и т. д.
Например, чтобы найти значение выражения:
120 : (5 · 3),
можно сначала разделить 120 на 5:
120 : 5 = 24,
а теперь, полученное частное 24 разделить на 3:
24 : 3 = 8,
значит 120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8.
Так как от перестановки множителей произведение не изменится, то множители можно поменять местами:
120 : (3 · 5)
и разделить 120 сначала на 3, а затем полученный результат разделить на 5:
120 : (3 · 5) = (120 : 3) : 5 = 40 : 5 = 8.
Получается, что не важно на какой множитель сначала делить число, результат будет одинаковым:
120 : (5 · 3) = (120 : 5) : 3 = 24 : 3 = 8
тоже самое, что и
120 : (5 · 3) = (120 : 3) : 5 = 40 : 5 = 8.
Из данного примера можно сделать вывод, что значение частного не изменится от порядка выполнения действий.
Деление суммы на число
Сумму можно разделить на число двумя способами:
1) Чтобы разделить сумму на какое-нибудь число, можно сначала вычислить значение суммы (выполнить сложение) и полученный результат разделить.
Например, чтобы найти значение выражения:
(15 + 12) : 3,
можно сначала сложить числа 15 и 12:
15 + 12 = 27
и полученную сумму разделить на 3:
27 : 3 = 9,
значит (15 + 12) : 3 = 27 : 3 = 9.
Если все слагаемые в записи суммы делятся на число, на которое надо разделить сумму, то можно воспользоваться вторым способом нахождения частного от деления суммы на число.
2) Чтобы разделить сумму на какое-нибудь число, можно разделить на это число каждое слагаемое отдельно и полученные частные сложить.
Например, чтобы найти значение выражения:
(42 + 28 + 70) : 7,
можно каждое слагаемое разделить на число 7:
42 : 7 = 6, 28 : 7 = 4 и 70 : 7 = 10;
и полученные частные (6, 4 и 10) сложить:
6 + 4 + 10 = 20,
значит (42 + 28 + 70) : 7 = 42 : 7 + 28 : 7 + 70 : 7 = 6 + 4 + 10 = 20.
Деление разности на число
Разность можно разделить на число двумя способами:
1) Чтобы разделить разность на какое-нибудь число, можно сначала вычислить значение разности (выполнить вычитание) и полученный результат разделить.
Например, чтобы найти значение выражения:
(24 – 8) : 2,
можно сначала вычесть из 24 число 8:
24 – 8 = 16,
и полученную разность разделить на 2:
16 : 2 = 8,
значит (24 – 8) : 2 = 16 : 2 = 8.
Если и уменьшаемое и вычитаемое в записи разности делятся на число, на которое надо разделить разность, то можно воспользоваться вторым способом нахождения частного от деления разности на число.
2) Чтобы разделить разность на какое-нибудь число, можно разделить на это число отдельно уменьшаемое и вычитаемое, а потом из первого частного вычесть второе.
Например, чтобы найти значение выражения:
(42 – 28) : 7,
можно отдельно уменьшаемое и вычитаемое разделить на число 7:
42 : 7 = 6, 28 : 7 = 4
и найти разность полученных частных:
6 – 4 = 2,
значит (42 – 28) : 7 = 42 : 7 – 28 : 7 = 6 – 4 = 2.
Общие формулы свойств деления
Все свойства деления можно представить в виде формул:
| Распределительные свойства | |
|---|---|
| (a + b) : c = a : c + b : c | |
| (a – b) : c = a : c – b : c | |
| (a · b) : c = (a : c) · b = (b : c) · a | |
| a : (b · c) = (a : b) : c = (a : c) : b | |
| Действия с единицей и нулём | |
| a : 1 = a | |
| a : a = 1 | |
| 0 : a = 0 (a ≠ 0) | |
| На нуль делить нельзя | |
Источник
Привет, мой друг, тебе интересно узнать все про свойства умножения, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
свойства умножения,свойства деления , настоятельно рекомендую прочитать все из категории Арифметика
. Об этом говорит сайт https://intellect.icu
свойства умножения
Переместительное свойство умножения
От перестановки множителей произведение не меняется.
a • b = b • a
Сочетательное свойство умножения
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
a • (b • c) = (a • b) • c
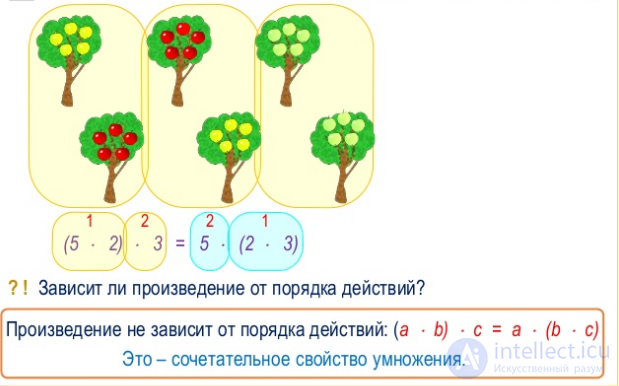
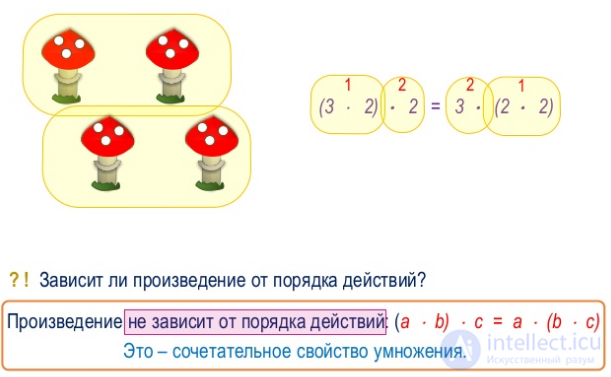
Переместительное и сочетательное свойства умноженияпозволяют сформулировать правило преобразования произведений.
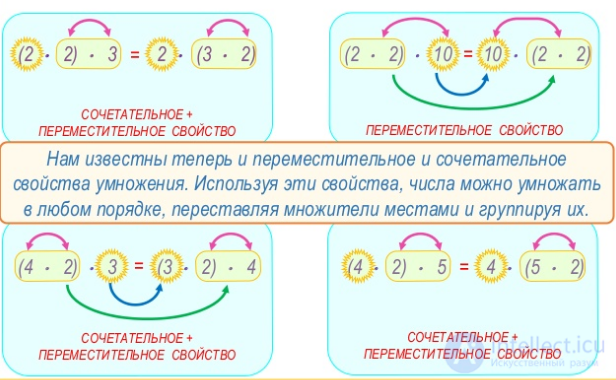
При умножении нескольких чисел, их можно как угодно переставлять и объединять в группы.
Свойство нуля при умножении
Если в произведении хотя бы один множитель равен нулю, то само произведение будет равно нулю.
a • 0 = 0
0 • a • b • c = 0
Распределительное свойство умножения относительно сложения
Чтобы умножить сумму на число, можно умножить на это число каждое слагаемое и сложить полученные результаты.
(a + b) • c = a • c + b • c
Это свойство справедливо для любого количества слагаемых.
(a + b + с + d) • k = a • k + b • k + c • k + d • k
Распределительное свойство умножения относительно вычитания
Чтобы умножить разность на число, можно умножить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе.
В буквенном виде свойство записывается так:
(a – b) • c = a • c – b • c
Чтобы умножить число на произведение двух чисел, можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель.
свойства деления
- Ни одно число нельзя делить на нуль.
- При делении нуля на число получается нуль.
0 : a = 0 - При делении любого числа на 1 получается это же число.
b : 1 = b


Если делимое и делитель умножить или разделить на одно и тоже натуральное число, то их частное не изменится.
a : b = (a • k) : (b • k), где k – любое натуральное число.
Обратите внимание, что именно свойство деления выше позволяет намсокращать дроби.
Использование всех рассмотренных выше свойств позволяет нам выполнять упрощение выражений .



Задача
У Короля есть 45 мешков с золотыми монетами, в каждом мешке по 108 золотых монет.
Он хочет разделить эти деньги поровну между своими тремя сыновьями.
Сколько золотых монет достанется каждому из принцев?
Решение 1
1)45:3=15(мешков) достанется мешков каждому принцу
2)15*108=1620(монет) достанется монет каждому принцу
Решение 2
1)45*108=4860(монет) всего монет у короля
2)4860:3=1620(монет) достанется монет каждому принцу
Решение 3
1)108:3=36(монет) каждому принцу, если делить один мешок
2)36*45=1620(монет) достанется монет каждому принцу
Пожалуйста, пиши комментарии, если ты обнаружил что-то неправильное или если ты желаешь поделиться дополнительной информацией про свойства умножения Надеюсь, что теперь ты понял что такое свойства умножения,свойства деления
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятелно рекомендую изучить комплексно всю информацию в категории
Арифметика
Источник
