Какие бывают свойства умножения
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a – b) = m · a – m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a – b) · m = a · m – b · m.
Переход от умножения:
m · (a + b) и m · (a – b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a – m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a – m · b
к умножению:
m · (a + b) и m · (a – b)
называется вынесением общего множителя за скобки.
Источник
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a·b=b·a
a и b – любые натуральные числа.
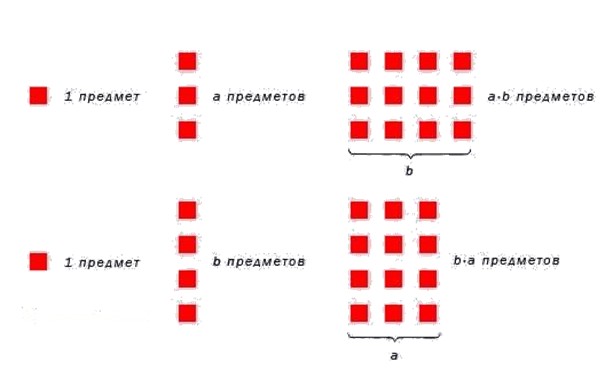
Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение 2·6. По определению произведения, нужно число 2 повторить 6 раз. Получаем: 2·6=2+2+2+2+2+2=12. Теперь поменяем множители местами. 6·2=6+6=12. Очевидно, переместительный закон выполняется.
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.

Сочетательное свойство умножения натуральных чисел
Второе название для сочетательного свойства умножения – ассоциативный закон, или ассоциативное свойство. Вот его формулировка.
Сочетательный закон умножения
Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c.
Приведем формулировку в буквенном виде:
a·b·c=a·b·c
a, b, c – любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.
Для наглядности приведем пример. Сначала вычислим значение 4·3·2.
4·3·2=4·6=4+4+4+4+4+4=24
Теперь переставим скобки и вычислим значение 4·3·2.
4·3·2=12·2=12+12=24
4·3·2=4·3·2
Как видим, теория совпадает с практикой, и свойство справедливо.
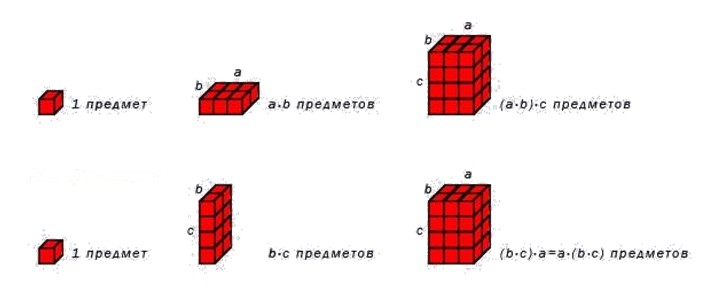
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b+c=a·b+a·c
a, b, c – любые натуральные числа.
Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4·3+2.
4·3+2=4·3+4·2=12+8=20
С другой стороны 4·3+2=4·5=20. Справедливость распределительного свойства умножения относительно сложения показана наглядно.
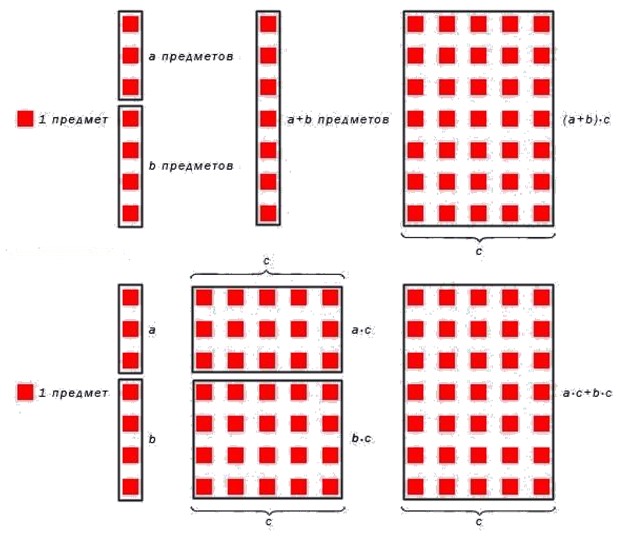
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Умножения разности чисел b и c на число a равносильно разности произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b-c=a·b-a·c
a, b, c – любые натуральные числа.
В предыдущем примере заменим “плюс” на “минус” и запишем:
4·3-2=4·3-4·2=12-8=4
С другой стороны 4·3-2=4·1=4. Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.
Умножение единицы на натуральное число
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
1·a=a
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
1·a=∑i=1a1
Умножение натурального числа a на единицу представляет собой сумму, состоящую из одого слагаемого a. Таким образом, переместительное свойство умножения остается справедливым:
1·a=a·1=a
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
Произведение числа 0 и любого натурального числа a равно числу 0.
0·a=0.
По определению, произведение 0·a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0·498=0; 0·9638854785885=0
Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: a·0=0.
Источник
4 класс
Предмет: Математика.
Тема: «Свойства умножения. Умножение на 0 и 1».
Цель урока: Создание условий для формирования знаний, умений и навыков учащихся по теме «Свойства умножения. Умножение на 0 и 1».
Задачи:
Предметные:
Познакомить со свойствами умножения (переместительный закон, сочетательный закон, распределительный закон, умножение на 0 и 1);
Научить использовать свойства арифметических действий при выполнении вычислений;
Научить выполнять умножение многозначного числа на однозначное, используя свойства умножения;
Личностные:
Помочь учащимся осознать социальную, практическую и личностную значимость учебного материала.
Регулятивные:
Создать условия для развития у школьников умений формулировать проблемы, предлагать пути их решения;
Содействовать развитию у школьников умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.
Коммуникативные:
Содействовать развитию у школьников умений общаться;
Обеспечить развитие у школьников монологической и диалогической речи.
Оборудование: учебник М.И Моро. «Математика». 4 класс. Учебник. В 2-х частях.; карточки самооценки, карточки с заданиями, карточки-помощники, интерактивная доска
САМОАНАЛИЗ УРОКА
В теме «Умножение. Свойства умножения» — 1 урок. Подойдя к теме урока, дети умеют:
называть компоненты и результаты умножения,
записывать сложение одинаковых слагаемых с помощью действия умножения и, наоборот, умножение переводить в действие сложения;
читать числовые равенства на умножение;
соотносить числовые выражения и равенства на умножение с предметными и схематическими моделями.
Научатся на уроке:
применять свойства умножения при вычислении и сравнении выражений;
объяснять конкретный смысл умножения при решении выражений.
Тип урока: объяснение нового материала.
Формы организации:
фронтальная;
индивидуальная;
работа в парах;
обратная связь.
групповая работа
Методы работы:
По характеру познавательной деятельности:
Частично-поисковый;
По источнику знаний:
Словесный (работа с учебником, текстом на доске), наглядный (демонстрация) и практический (упражнения, самостоятельная работа).
По дидактической цели:
Получение новых знаний.
По месту в структуре деятельности:
Стимулирование и мотивация.
Контроль — обратная связь, взаимоконтроль, самоконтроль.
Ожидаемые результаты:
понимание детьми, что знание свойства умножения помогает совершать вычисления удобнее и быстрее;
повышение активности детей в урочной деятельности;
повышение уровня взаимоконтроля и самоконтроля.
(По конспекту — УУД)
Содержание учебных заданий соответствует возможностям детей и типу класса, позволяет работать в зоне ближайшего развития детей.
Урок построен по системно- деятельностному подходу — не передача знаний, а управление учебной деятельностью; признание решающей роли учебного сотрудничества в достижении целей обучения.
На данном уроке были использованы различные способы активизации познавательной деятельности учащихся. Учащиеся проявляли активность и выступали в роли субъектов деятельности. Если вернемся к задачам, которые были поставлены в начале урока:
Задачи урока были выполнены.
Ход урока:
Этап:
Деятельность учителя:
Деятельность обучающихся:
Универсальные действия:
Актуализация знаний
Организационный момент. (Повторение)
Приветствие.
– – Запишите число, «Классная работа».
Прочитайте раздел (1 слайд)
-Как вы думаете, с какими арифметическими действиями мы будем сегодня работать?
Начнем с устного счета (2слайд) Вспомним таблицу умножения с зимнем видом спорта.
Тренажёр 3-15
Сейчас вы поработаете в парах. Посмотрите на выражения, скажите, чем они похожи? Чем отличаются? (16 слайд)
Запишите выражения по группам в тетради, выполните задание
34+18+44
31+31+31=31*3
17+17+17+17=17*4
31+32+33+34
28+28=28*2
X+x+x+x+x=x*5
проверка
-Та пара, которая выполнила первая отвечает вместе.
– Проверьте результат работы.
оргмомент
Рассматривают выражения и выполняют задания в паре в тетрадях.
Называют ответы.
Проверяют и оценивают результат.
Личностные: самоопределение; регулятивные: целеполагание; планирование, контроль коррекция, оценка;
коммуникативные: планирование учебного сотрудничества с учителем и сверстниками
умение выражать и отстаивать свою точку зрения в диалоге с партнёрами; умение вступать в сотрудничество, согласовывать действия с партнёром, выражать и отстаивать свою точку зрения и отстаивать её в диалоге;
Постановка учебной задачи и целей урока
– Мы переходим на второй этап урока.
– Это новый для вас раздел или вы уже знакомы с умножением?
– У вас на партах лежат схемы, которые вам нужно будет заполнить в течение урока. ( слайд 17)
– Прочитайте тему урока и скажите,
свойства какого арифметического действия вам уже знакомы?
Давайте их вспомним
слайд 18
– На экране даны выражения: нужно найти выражения между которыми можно поставить знак равно без вычисления.
Если обозначить буквами цифры получится выражение.
-Как называется это свойство сложения?
слайд 19
–Какие числа сначала удобнее прибавить? А потом?
Как называется это свойство?
Физминутка для глаз ( слайд 20)
-Зачем мы повторили свойства сложения?
(сами говорят тему урока)слайд 21
– Какие цели на урок мы поставим для себя? (слайд 22)
РАЗДЕЛ: УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
Тема: Умножение на однозначное число
-свойства сложения
ФРОНТАЛЬНАЯ РАБОТА.
Находят и читают свойства.
По слайдам 5-6
-переместительное
–сочетательное
Определяют тему урока:
Свойства умножения.
Определяют цели урока: Сформулировать свойства умножения;
Научиться использовать свойства арифметических действий при выполнении вычислений;
Научиться выполнять умножение многозначного числа на однозначное, используя свойства умножения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; познавательные: логические – анализ объектов с целью выделения признаков;
постановка и формулирование проблемы; анализ, синтез;
регулятивные: целеполагание, прогнозирование.
Работа с новым материалом. Первичное закрепление.
Начнем знакомство со свойствами умножения
салйд 23
–Посмотрите на пример и скажите, как удобнее умножить
Какой закон позволяет менять множители местами?
-Сформулируйте переместительное свойство умножения;
Слайд 24
Запишите свойство с помощью букв в вашу схему.
слайд 25
– Запишите вычисления в столбик по рядам.(3 человека на доске)
1 ряд: 6•409=2454
2 ряд: 4·580=2320
3 ряд: 7•320=2240
запись на доске
слайд 26
-Посмотрите на пример и скажите, какие числа удобнее умножить сначала,а потом какое?
Сочетательное свойство умножения;
слайд 27
Запишите свойство в схему
Слайд 28
Закрепление свойства- по вариантам(взаимопроверка)
Умножение на 0 и 1.
слайд 29-34
Заполните свою схему
Распределительное свойство умножения;
Слайды 35-38
Запишите свойство в схему
Слайд 39 закрепление всех свойств- решение по карточкам
-Переместительный закон.
П: От перестановки мест множителей произведение не меняется.
От каждого ряда ученик решает на доске
Работа по ИД
Проверка
: Множители можно объединять в группы любым способом.
Фронтальная работа сл.15
Р: Чтобы умножить сумму на число, надо каждое слагаемое умножить на это число.
Решение примеров по вариантам
Индив работа
Проверка по интер доске
Отработка полученных знаний, подведение итогов
Слайд 40 Сделайте итог вашей работы:
Назовите тему сегодняшнего урока
Расскажите свойства умножения, пользуясь своей схемой.
Зачем нужно знать свойства умножения?
Сможете ли вы самостоятельно применять эти свойства?
Как легче учить правила: по учебнику или по своим схемам?
Ответы учащихся
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками;
познавательные:
осознанное и произвольное построение речевого высказывания;
установление причинно-следственных связей, построение логической цепи рассуждений, доказательств.
регулятивные:
Оценка
Закрепление изученного.
Вы познакомились со свойствами умножения. Выполните задания по карточкам, используя эти свойства. Карточки положите в тетрадь и сдайте в конце урока.
Выполняют работу по карточкам 3 варианта
познавательные:
смысловое чтение как осмысление цели чтения и выбор вида чтения в зависимости от цели; выделение необходимой информации из текста, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
регулятивные:
коррекция, оценка
Рефлексия деятельности (итог урока).
41 слайд
Перед вами лежит отметочница, подпишите ее, оцените свою работу на уроке, отметьте с помощью галочки ваши позиции.
Делают рефлексию своей работы.
Личностные:
Смыслообразование, нравственно-этическое оценивание;
.
Домашнее задание.
пр 331 задача 329 стр 76
Записывают д/з в дневниках.
Личностные: самоопределение.
Дополнительно карточки с заданиями (можно использовать на следующем уроке)
Карточка 2
1 задание.
Объясни, почему верны равенства (выбери правильный ответ из предложенных)
10 ∙ 5 ∙ 3 = 3 ∙ 5 ∙ 10
Распределительное: при умножении суммы на число можно умножить на него каждое слагаемое
Сочетательное: два соседних множителя можно заменить их произведением
Переместительное: от перестановки множителей произведение не изменяется
2 задание.
Объясни, почему верны равенства (выбери правильный ответ из предложенных)
10 ∙ (5 ∙ 3) = (10 ∙ 5) ∙ 3
Распределительное: при умножении суммы на число можно умножить на него каждое слагаемое
Сочетательное: два соседних множителя можно заменить их произведением
Переместительное: от перестановки множителей произведение не изменяется
3 задание.
Объясни, почему верны равенства (выбери правильный ответ из предложенных)
(10 + 5) ∙ 3 = 10 ∙ 3 + 5 ∙ 3
Распределительное: при умножении суммы на число можно умножить на него каждое слагаемое
Сочетательное: два соседних множителя можно заменить их произведением
Переместительное: от перестановки множителей произведение не изменяется
Карточка 3
Распределите примеры по столбикам в зависимости от того, какое свойство сложения нужно применять для решения каждого выражения., запишите каждый в свою тетрадь
Переместительный Сочетательный Распределительный Умножение на 0 и 1.
4 ∙ 356, (5 + 12) ∙ 4,
15 ∙ (4 + 10), 7 ∙ 12 ∙ 5,
16 ∙ 15 ∙ 4 ∙ 5, 6 ∙ 229
0∙249 887 ∙1
Карточка 1
Выполните умножение в парах.
2500 + 60 + 8=
100: 2 =
1 000 : 100 =
7 + 100 + 1000 =
100 • 5 =
100*128=
9600 + 400 =
6 • 40 =
200:4-
3 000 + 9 000 =
11 • 9 =
35*100=
Источник
4 В класс 2017г.
Предмет: Математика.
Тема: «Свойства умножения».
Цель урока: Создать условия для формирования знаний, умений и навыков учащихся по теме «Свойства умножения».
Задачи:
Предметные:
Повторить свойства умножения (переместительный закон, сочетальный закон, распределительный закон, умножение на 0 и 1);
Научить использовать свойства арифметических действий при выполнении вычислений;
Научить выполнять умножение многозначного числа на однозначное, используя свойства умножения;
Личностные:
Помочь учащимся осознать социальную, практическую и личностную значимость учебного материала.
Регулятивные:
Создать условия для развития у школьников умений формулировать проблемы, предлагать пути их решения;
Содействовать развитию у школьников умений осуществлять самоконтроль, самооценку и самокоррекцию учебной деятельности.
Коммуникативные:
Содействовать развитию у школьников умений общаться;
Обеспечить развитие у школьников монологической и диалогической речи.
Оборудование: учебник М. И. Башмаков, М. Г. Нефедова. «Математика». 4 класс. Учебник. В 2-х частях.; карточки самооценки, карточки с заданиями.
Ход урока:
Этап:
Деятельность учителя:
Деятельность обучающихся:
Универсальные действия:
Актуализация знаний
Организационный момент. (Повторение)
Приветствие.
-Желаю, чтобы глаз у вас был острым, ум гибким, а знания, которые вы приобретёте на уроке – крепкими.
– Запишите число, «Классная работа».
-Вспомним наши этапы урока. Сейчас работает с этапом 1. Повторение.
Сейчас вы работаете в парах. На партах карточки с заданиями. Возьмите карточку 1. Выполните умножение в парах. Ответ записывать прямо на листках.
Оцените работу в группу до выполнения задания (прогноз).
2500 + 60 + 8 100: 2 1 000 : 100
7 + 100 + 1000 100 • 5 100*128
9600 + 400 6 • 40 200:4
3 000 + 9 000 11 • 9 35*100
-Та пара, которая выполнила первая отвечает вместе.
-Оцените результат работы. У кого обе оценки совпали? У кого прогноз лучше, чем результат? У кого результат лучше, чем прогноз?
Называют этапы:
Актуализация знаний,
Постановка учебной задачи,
Работа с новым материалом. (Первичное закрепление),
Закрепление знаний.
Рассматривают карточки и выполняют задания устного счета в паре на листках. Прогнозируют свою работу в группе.
Называют ответы:
2 568, 50,10, 1107, 500,
12 800,10 000, 240, 50, 12 000, 99,3 500.
Оценивают результат.
Личностные: самоопределение; регулятивные: целеполагание; коммуникативные: планирование учебного сотрудничества с учителем и сверстниками
Постановка учебной задачи.
– Мы переходим на второй этап урока. В какой раздел математики мы начали вчера свое путешествие?
– Это новый для вас раздел или вы уже знакомы с умножением и делением?
– Посмотрите на равенства. Прежде чем мы с ними начнём работать, обратите внимание на математические действия. Какие действия встречаются в этих выражениях?
– Распределите выражения на пять столбиков. По какому признаку мы это сделаем?
(105 • 2) •3 =105 • (2 •3) Сочетальный закон У
13 • 25 = 25 •13 Переместительный закон У
(45+264) •2=45•2+264•2 Распределительный закон У
284•0=0 Умножение числа на 0
1•578=578 Умножение на 1
-Сформулируйте переместительное свойство умножения; Сочетательное свойство умножения; Распределительное свойство умножения; Умножение на 0 и 1.
– Зачем нужно знать свойства в математике?
– Какая тема нашего урока сегодня?
– Какие цели на урок мы поставим для себя?
РАЗДЕЛ: УМНОЖЕНИЕ И ДЕЛЕНИЕ МНОГОЗНАЧНЫХ ЧИСЕЛ
Тема: Умножение на однозначное число
ФРОНТАЛЬНАЯ РАБОТА.
Находят и читают свойства.
П: От перестановки мест множителей произведение не меняется.
С: Множители можно объединять в группы любым способом.
Р: Чтобы умножить сумму на число, надо каждое слагаемое умножить на это число.
Чтобы облегчить решение.
Определяют тему урока:
Свойства умножения.
Определяют цели урока: Повторить свойства умножения; Научиться использовать свойства арифметических действий при выполнении вычислений; Научиться выполнять умножение многозначного числа на однозначное, используя свойства умножения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; познавательные: логические – анализ объектов с целью выделения признаков;
постановка и формулирование проблемы; анализ, синтез;
регулятивные: целеполагание, прогнозирование.
Работа с новым материалом. Первичное закрепление.
– Переходим на этап 3. Откройте учебники на стр. 74, замените наши примеры с помощью латинских букв.
Прочитаем еще раз формулировку свойств умножения.
– В учебнике найдите № 1.Дан пример.3*6 857. Какая запись удобнее для вычислений?
-Какой закон позволяет менять множители местами?
– Запишите вычисления в столбик по рядам.
1 ряд: 3•6857
2 ряд: 6•4095
3 ряд: 7580•4
Кто решит быстро делают 4 пример.
а•в=в•а
(а•в) •с=а•(в•с )
(а+в )•с=а•с + в•с
а•0=0
0•а=0
а•1=а
1•а=а
Третья запись.
Переместительный закон.
20 571
24 570
30 320
104 020
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками;
познавательные:
осознанное и произвольное построение речевого высказывания;
установление причинно-следственных связей, построение логической цепи рассуждений, доказательств.
Физкультминутка.
Вызываю дежурного. Проводит физкультминутку.
Выполняют все вместе минутку отдыха.
Отработка полученных знаний.
-Какова тема урока? А цель?
Посмотрите на № 2. Выполним вычисления устно. Объясните, как провели вычисления. Продолжите.
-Какие математические законы вы использовали при этих вычислениях?
-Рассмотрим задание № 4. Прочитайте задачу про себя. Одного ученика вызываю решать у доски. Ученик Оценивает себя перед решением задачи.
Дополнительно: стр.75 № 9. Сдадут после урока тетради.
Формулируют тему урока,цель.
5*30=5*3*10=15*10=150
700*6=7*100*6=7*6*100=
42*100=4 200
12*50=12*5*10=60*10=600
200*34=2*100*34=2*34*100
=68*100=6800
Переместительный и сочетательный закон умножения.
1).16*9=144 (пл.) -в 9 подъездах.
2)144*8=1 152 (кв.)
Ответ:1 152 квартиры в доме.
Физкультминутка
Для глаз и шеи. Проводят самостоятельно.
Выполняют все вместе минутку отдыха.
Закрепление изученного.
Работа в паре.
Работа в группах.
– Переходим к этапу 4. Вспомним нашу тему и цель урока.
. Сейчас вы будете работать в парах.
-Каждая пара возьмёт карточку 2 и прочитает задание.
-Всё ли вам понятно в задании? Задайте вопрос, если возникли трудности в понимании задания.
-Сделайте прогноз вашей работы.
-Проверка.
– Оцените результат вашу работу в паре на карте самооценки.
Называют тему урока, цель урока.
Выполняют задание в парах. Прогнозируют свою работу. Оценивают результат.
Переместительное свойство У,
Сочетательное свойство У,
Распределительный закон У.
Коммуникативные:
умение выражать и отстаивать свою точку зрения в диалоге с партнёрами; умение вступать в сотрудничество, согласовывать действия с партнёром, выражать и отстаивать свою точку зрения и отстаивать её в диалоге;
познавательные:
смысловое чтение как осмысление цели чтения и выбор вида чтения в зависимости от цели; выделение необходимой информации из текста, выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
регулятивные:
планирование, контроль коррекция, оценка;
-А сейчас вы поработаете в группе. Возьмите карточку 3, прочитайте задание в группе. Задайте вопрос, если возникли трудности в понимании задания. Спрогнозируйте результат.
-Начните выполнять задание.
-Проверим. При решении, каких выражений вы будете применять переместительное свойство умножения, объясните, почему вы так думаете?
–Сочетательное свойство?
-Распределительное?
– Умножение на 0 и 1.
-Оцените результат.
Прогнозируют свою работу.
Садятся, выполняют задание.
Дают ответы, сравнивают, с эталоном.
П: 4 ∙ 356, 6 ∙ 229.
С: 16 ∙ 15 ∙ 4 ∙ 5, 7 ∙ 12 ∙ 5.
Р: (5 + 12) ∙ 4, 15 ∙ (4 + 10).
У: 0* 249, 887*1.
Оценивают результат.
Рефлексия деятельности (итог урока).
-Какова тема урока?
-Чему учились на уроке?
Сделайте итог вашей работы:
сегодня я узнал(а)…
было интересно…
было трудно…
я выполнял задания…
я понял, что…
теперь я могу…
я почувствовал(а), что…
я приобрел(а)…
я научился…
у меня получилось …
я смог…
я попробую…
меня удивило…
мне захотелось…
Определяют тему урока:
Свойства умножения.
Определяют цели урока: Повторить свойства умножения; Научиться использовать свойства арифметических действий при выполнении вычислений; Научиться выполнять умножение многозначного числа на однозначное, используя свойства умножения.
Делают рефлексию своей работы.
Личностные:
Смыслообразование, нравственно-этическое оценивание;
регулятивные:
Оценка.
Домашнее задание.
Стр.74-75 №3, 5.
Записывают д/з в дневниках.
Личностные: самоопределение.
Карточка 2
1 задание.
Объясни, почему верны равенства (выбери правильный ответ из предложенных)
10 ∙ 5 ∙ 3 = 3 ∙ 5 ∙ 10
Распределительное: при умножении суммы на число можно умножить на него каждое слагаемое
Сочетательное: два соседних множителя можно заменить их произведением
Переместительное: от перестановки множителей произведение не изменяется
2 задание.
Объясни, почему верны равенства (выбери правильный ответ из предложенных)
10 ∙ (5 ∙ 3) = (10 ∙ 5) ∙ 3
Распределительное: при умножении суммы на число можно умножить на него каждое слагаемое
Сочетательное: два соседних множителя можно заменить их произведением
Переместительное: от перестановки множителей произведение не изменяется
3 задание.
Объясни, почему верны равенства (выбери правильный ответ из предложенных)
(10 + 5) ∙ 3 = 10 ∙ 3 + 5 ∙ 3
Распределительное: при умножении суммы на число можно умножить на него каждое слагаемое
Сочетательное: два соседних множителя можно заменить их произведением
Переместительное: от перестановки множителей произведение не изменяется
Карточка 3
Распределите примеры по столбикам в зависимости от того, какое свойство сложения нужно применять для решения каждого выражения., запишите каждый в свою тетрадь
Переместительный Сочетательный Распределительный Умножение на 0 и 1.
4 ∙ 356, (5 + 12) ∙ 4,
15 ∙ (4 + 10), 7 ∙ 12 ∙ 5,
16 ∙ 15 ∙ 4 ∙ 5, 6 ∙ 229
0∙249 887 ∙1
Карточка 1
Выполните умножение в парах.
2500 + 60 + 8=
100: 2 =
1 000 : 100 =
7 + 100 + 1000 =
100 • 5 =
100*128=
9600 + 400 =
6 • 40 =
200:4-
3 000 + 9 000 =
11 • 9 =
35*100=
Источник
