Какие бывают свойства сложения и вычитания
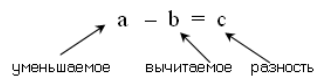
Сочетай, перемещай, свойства действий
узнавай
Напомним известные уже из арифметики главнейшие свойства действий сложения, вычитания, умножения и деления, так
как этими свойствами придется часто пользоваться и в алгебре.
Свойства сложения
Переместительный закон сложения
Сумма не изменяется от перестановки слагаемых .
Пример:
3 + 8 = 8 + 3; 5 + 2 + 4 = 2 + 5 + 4 = 4 + 2 + 5.
В общем случае:
a+b=b+a
a+b+c=c+a+b
Стоит иметь ввиду, что число слагаемых может быть и более трёх.
Сочетательный закон сложения
Сумма нескольких слагаемых не изменится, если какие-нибудь из них заменить их суммой .
Пример:
3 + 5 + 7 = 3 + (5 + 7) = 3 + 12 = 15;
4 + 7+11+6 + 5 = 7 +(4+ 5)+ (11+6) = 7 + 9+17 = 33.
В общем случае:
а + b + с = а+(b + с) = b+(а + с) и т. п.
Иногда этот закон выражают так: слагаемые можно соединять в какие угодно группы.
Чтобы прибавить к какому-либо числу сумму нескольких чисел, можно прибавить отдельно каждое слагаемое одно за другим.
Пример:
5 + (7 + 3) = (5 + 7) + 3 = 12 + 3 = 15.
В общем случае:
a+(b+c+d+…+x)=a+b+c+d+…+x
Свойства вычитания
Свойство вычитания суммы из числа
Чтобы вычесть из какого-нибудь числа сумму нескольких чисел, можно вычесть отдельно каждое слагаемое одно за другим.
Например:
20 — (5+ 8) = (20 — 5) — 8 = 15 — 8 = 7.
В общем случае:
а — (b + с + d+ …) = а — Ь — с — d — …
Свойство сложения разности чисел
Чтобы прибавить разность двух чисел, можно прибавить уменьшаемое и затем вычесть вычитаемое.
Пример:
8 + (11-5) = 8+ 11 -5= 14.
В общем случае:
а + (b — с) = а + Ь — с.
Свойство вычитания разности из числа
Чтобы вычесть разность, можно сначала прибавить вычитаемое и затем вычесть уменьшаемое.
Например:
18-(9-5) = 18 + 5-9= 14.
Вообще:
а — (Ь — с) = а + с — b.
Свойства умножения
Переместительный закон умножения
Произведение не изменится от перестановки сомножителей .
Так:
4·5 = 5·4; 3·2·5 = 2·3·5 = 5·3·2.
Вообще:
a*b = b*a; abc… =b*а*с*… = c*b*a* …
Сочетательный закон умножения
Произведение нескольких сомножителей не изменится, если какие-нибудь из них заменить их произведением .
Так:
7*3*5 = 5*(3*7) = 5*21 = 105.
Вообще:
abc = а(bс) = b(ас) и т. п.
Умножение числа на произведение чисел
Чтобы умножить какое-либо число на произведение нескольких сомножителей, можно умножить это число на
первый сомножитель, полученный результат умножить на второй сомножитель и т. д.
Так:
3*(5*4) = (3*5)*4= 15*4 = 60.
Вообще:
a•(bcd…) = {[(a·b)•c]•d}…
Чтобы умножить произведение нескольких сомножителей на какое-либо число, можно умножить на это число один
из сомножителей, оставив другие без изменения.
Так:
3 • 2 • 5 • 3 = (3 • 3) • 2 • 5 = 3 • (2 • 3) • 5 = 3 • 2 • (5 • 3).
Вообще:
(abc.. )m = (аm)bс… = а(bm)с… и т. п.
Умножение числа на сумму чисел
Чтобы умножить сумму на какое-либо число, можно каждое слагаемое умножить на это число и полученные ре-
результаты сложить.
Так:
(5 + 3)·7 = 5·7 + 3·7.
Вообще:
(а + b + с + .. .)n = an + bn + cn + …
В силу переместительного закона умножения это же свойство можно выразить так: чтобы умножить какое-либо число на
сумму нескольких чисел, можно умножить это число на каждое слагаемое отдельно и полученные результаты сложить.
Так:
5·(4 + 6) = 5·4 + 5·6.
Вообще:
r·(а + Ь + с +…) = rа + rb + rс + …
Это свойство называется распределительным законом умножения, так как умножение, производимое над суммой, распределяется на каждое слагаемое в отдельности.
Распределительный закон умножения для разности чисел
Распределительный закон можно применять и к разности.
Так:
(8 — 5) • 4 = 8 • 4 — 5 • 4;
7 • (9 — 6) = 7 • 9 — 7 • 6.
Вообще:
(а — b)с = ас — bc,
а(b — с) = ab — ас,
т. е. чтобы умножить разность на какое-либо число, можно умножить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй; чтобы умножить какое-либо число на разность, можно это число умножить
отдельно на уменьшаемое и вычитаемое и из первого результата вычесть второй.
Свойства деления
Деление суммы на число
Чтобы разделить сумму на какое-либо число, можно разделить на это число каждое слагаемое отдельно и полученные результаты сложить:
Например:
(30+12+5)/3=30/3+12/3+5/3
Вообще:
(a+b+c+…+v)/m= (a/m)+(b/m)+(c/m)+…(v/m)
Деление разности на число
Чтобы разделить разность на какое-либо число, можно разделить на это число отдельно уменьшаемое и вычитаемое
и из первого результата вычесть второй:
(20-8)/5= 20/5 — 8/5
Вообще:
(a-b)/c = (a/c) -(b/c)
Деление произведения на число
Чтобы разделить произведение нескольких сомножителей на какое-либо число, можно разделить на это число один
из сомножителей, оставив другие без изменения:
(40 • 12 • 8) : 4 = (40:4) • 12 • 8 = 10 • 12 • 8 = 40 • 12 • 2.
Вообще:
(a·b·c…) : t = (а : t)bс… = а(b : t)с… и т. д.
Деление числа на произведение
Чтобы разделить какое-либо число на произведение нескольких сомножителей, можно разделить это число на
первый сомножитель, полученный результат разделить на второй сомножитель и т.д.:
120 : (12 • 5 • 3) = [(120 : 2) : 5] : 3 = (60 : 5) : 3 = 12 : 3 = 4.
Вообще:
а : (bcd …) = [(а : b) : с] : d… и т. п.
Укажем еще следующее свойство деления:
Если делимое и делитель умножим (или разделим) на одно и то же число, то частное не изменится.
Поясним это свойство на следующих двух примерах:
1)8:3 = 8/3|,
умножим делимое и делитель, положим, на 5; тогда получим
новое частное: (8*5)/(3*5)
которое по сокращении дроби на 5 даст прежнее частное — 8/3
Вообще, какие бы числа a, b и m ни были, всегда
(am) : (bm) = а : b, что можно написать и так:
am/bm= a/b
Если частное не изменяется от умножения делимого и делителя на одно и то же число, то оно не изменяется и от деления делимого и делителя на одно и то же число, так как деление на какое-нибудь число равносильно умножению на обратное число.
Комментирование и размещение ссылок запрещено.
Источник
Сложение натуральных чисел
Для получения числа, которое следует за натуральным, нужно прибавить к нему единицу.
Пример 1
$5 + 1 = 6;$
$48 + 1 = 49$
Для сложения чисел $9$ и $3$ нужно к числу $9$ прибавить $3$ раза единицу.
Получим:
$9 + 3 = 9 + 1 + 1 + 1 = 10 + 1 +1 = 11 + 1 = 12.$
Записывают короче:
$9 + 3 = 12.$
Числа, которые складывают, называют слагаемыми, а результат их сложения — суммой.
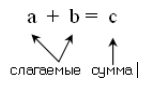
Рисунок 1.
В примере $9 + 3 = 12$:
$9$ и $3$ — слагаемые, $6$ — сумма.
Свойства сложения
Переместительное свойство (коммутативность):
При перестановке слагаемых сумма не меняется
$1 + 5 = 5 + 1 = 6.$
В общем виде переместительное свойство записывается так:
$a + b = b + a$.
Сочетательное свойство (ассоциативность):
Сумма трех и более слагаемых не изменится, если изменить порядок их сложения
$2 + ( 8 + 3 ) = ( 2 + 8 ) + 3 = 13.$
В общем виде сочетательное свойство записывается так:
$a + ( b + c ) = ( a + b ) + c.$
Свойство прибавления нуля:
Если к числу прибавить нуль, то сумма будет равна самому числу
$7 + 0 = 7.$
К этому свойству можно применить переместительное свойство, получим:
Если к нулю прибавить число, то сумма будет равна прибавляемому числу
$0 + 7 = 7.$
В общем виде:
$a + 0 = 0 + a = a.$
Если точкой $C$ разделить отрезок $AB$, то сумма длин отрезков $AC$ и $CB$ будет равна длине отрезка $AB$.

Рисунок 2.
Записывается: $AB = AC + CB$.
Сложение чисел можно удобно выполнять «в столбик»:

Рисунок 3.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Вычитание натуральных чисел
Вычитание — операция, обратная сложению.
Пример 2
На тарелке лежало $7$ яблок, съели $3$ яблока. Сколько яблок осталось на тарелке?
Очевидно, что если к оставшемуся числу яблок $(x)$ добавить $3$ яблока, то их станет $7$:
$x + 3 = 7.$
Таким образом, известно одно слагаемое и сумма, нужно найти второе слагаемое.
Для этого используется вычитание:
$x = 7 – 3 = 4$, т.к. $3 + 4 = 7.$
Число, из которого вычитают, называется уменьшаемым, а число, которое вычитают, — вычитаемым. Результат вычитания называется разностью.
Из данной задачи получаем:
$7$ — уменьшаемое, $3$ — вычитаемое, $8$ — разность.
В общем виде
Если $b + c = a$, то

Рисунок 4.
При вычитании натуральных чисел уменьшаемое обязательно должно быть больше вычитаемого:
$11 – 3 = 8; 8 > 3.$
Разность двух чисел находят, чтобы узнать на сколько уменьшаемое больше вычитаемого или на сколько вычитаемое меньше уменьшаемого:
$11$ больше $3$ на $8$.
Свойства вычитания
Свойство вычитания суммы из числа:
$a – ( b + c ) = a – b – c.$
Например, нужно найти значение выражения:
$123 – ( 23 + 45 ) = 123 – 68 = 55.$
Однако намного удобнее считать так:
$123 – ( 23 + 45 ) = 123 – 23 – 45 = 100 – 45 = 55.$
В этом выражении нужно вычесть сумму из числа, а можно сначала вычесть из уменьшаемого одно слагаемое, а потом из полученной разности вычесть второе слагаемое.
Например, найдем результат выражения:
$217 – 33 – 27 = 184 – 27 = 157.$
Но гораздо легче найти сумму вычитаемых и вычесть ее из уменьшаемого:
$217 – 33 – 23 = 217 – ( 33 + 27 ) = 217 – 60 = 157.$
Свойство вычитания числа из суммы:
если $c
если $c
Рассмотрим три примера с одинаковыми результатами.
$( 6 + 5 ) – 4=11 – 4=7;$
$6 + ( 5 – 4 )=6 + 1=7;$
$( 6 – 4 ) + 5=2 + 5=7.$
Откуда получаем: $( 6 + 5 ) – 4=6 + ( 5 – 4 )=( 6 – 4 ) + 5.$
Если нужно вычесть число из суммы, можно вычесть его из любого слагаемого и к полученной разности прибавить другое слагаемое.
Вычитаемое обязательно должно быть меньше слагаемого, из которого его вычитают, или равным ему.
Пример 3
$( 234 + 123 ) – 134=357 – 134=223.$
Но намного удобнее считать так:
$( 234 + 123 ) – 134=234 – 134+ 123=100+ 123=223.$
Если из числа вычесть нуль, оно не изменится:
$a – 0 = a.$
Если из числа вычесть это же число, получим нуль:
$a – a = 0.$
Т.к. $9 + 0 = 9$, то по смыслу вычитания имеем:
$9 – 9 = 0$ или $9 – 0 = 9.$
Результат вычитания удобно находить «в столбик»:
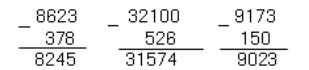
Рисунок 5.
Если точкой $C$ разделяется отрезок $AB$, то разность длин отрезков $AB$ и CB$ равна длине отрезка $AC.$

Рисунок 6.
Записывается: $AB – CB = AC$ или $AB – AC = CB.$
Если $AB = 7$ см, а $CB = 4$ см, то $AC = 7 – 4 = 3$ см.
Пример 4
Решить уравнение $63 – x = 55.$
Решение:
$x = 63 – 55$, откуда $x = 8.$
Число $8$ называется корнем уравнения $63 – x = 55$, т.к. получаем верное равенство $63 – 8 = 55.$
Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность.
Источник
Умножение, сложение, вычитание и деление – основные операции с целыми числами. Результаты этих операций с любыми целыми числами обладают рядом характеристик. Иначе говоря, операции умножения, сложения, вычитания и деления целых чисел обладают свойствами. Данная статья посвящена рассмотрению основных свойств умножения, сложения, вычитания и деления целых чисел.
Сложение целых чисел. Основные свойства
Все свойства сложения натуральных чисел оказываются справедливы и для целых чисел. Ведь множество целых чисел ℤ включает в себя множество натуральных чисел ℕ. Приведем ниже основные свойства сложения.
Коммутативное свойство сложения
Переместительное (коммутативное свойство) или переместительный закон.
От перемены мест слагаемых сумма не меняется.
a+b=b+a
Согласно этому свойству, справедливо равенство:
35+251=251+35
Свойство коммутативности работает вне зависимости от знака.
-528+3700=3700+-528
Ассоциативное свойство сложения
Сочетательное (ассоциативное свойство) или сочетательный закон.
Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.
a+b+c=a+b+c
Примечание: данное свойство применимо и для большего количества слагаемых.
Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:
64+81+(-49)=64+81+(-49)=64+81+(-49);
(128+(-75))+96=128+((-75)+96).
Свойства сложения, связанные с числом 0
1. Число нуль – нейтральный по сложению элемент.
Прибавление нуля к любому целому числу не меняет этого числа.
a+0=a
2. Сумма любого целого числа и противоположного ему числа равна нулю.
a+(-a)=0
Умножение целых чисел. Основные свойства
Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.
Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.
Переместительное свойство умножения
От перемены мест множителей произведение не меняется.
a·b=b·a
Приведем пример. Очевидно, что произведение целых чисел 2·3 эквивалентно произведению 3·2.
Сочетательное свойство умножения
Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:
a·(b·c)=(a·b)·c
a, b, c – произвольные целые числа.
Примечание: данное свойство применимо и для большего количества множителей.
В соответствии с этим свойством можно говорить о справедливости следующих равенств:
-12·3·8=-12·3·8;
119·((-251)·36)=(119·(-251))·36.
Умножение числа на нуль
Результатом умножения любого целого числа на нуль является число нуль.
a·0=0
Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.
a·b=0 если a=0 или b=0.
Умножение числа на единицу
Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.
a·1=a
Распределительное свойство умножения относительно суммы.
Произведение целого числа a на сумму двух чисел b и c равно сумме произведений a·b и a·c.
a·(b+c)=a·b+a·c
Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.
В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.
Вычитание целых чисел. Основные свойства
Вычитание – действие, обратное сложению. Число c является разностью двух чисел a и b тогда, когда сумма b+c равна a. Можно сказать, что разность чисел a и b – это сумма чисел a и -b. Свойства вычитания являются следствием свойств сложения и умножения.
Основные свойства вычитания
- Вычитание чисел не обладает переместительным свойством за исключением случая, когда a=b. a-b≠b-a.
- Разность целых чисел, равных друг другу: a-a=0.
- Вычитание суммы двух чисел из другого числа: a-(b+c)=a-b-c.
- Вычитание целого числа из суммы: a+b-c=a-c+b=a+(b-c).
- Распределительное свойство умножения относительно вычитания: a·(b-c)=a·b-a·c.
Деление целых чисел. Основные свойства
Деление – операция, обратная умножению. Число c называется частным от деления чисел a и b, когда произведение b·c равно a. Запишем основные свойства деления целых чисел.
Основные свойства деления
- Деление на нуль невозможно.
- Деление нуля на число: 0a=0.
- Деление равных чисел: aa=1.
- Деление на единицу: a1=a.
- Для деления переместительное свойства не выполняется: ab≠ba.
- Деление суммы и разности на число: a±bc=ac±bc.
- Деление произведения на число: a·bc=ac·b, если a делится на c; a·bc=a·bс, если b делится на c; a·bc=a·bс=ac·b, если a и b делятся на c.
- Деление числа на произведение: ab·c=ab·1c=ac·1b.
Источник
Содержание:
- § 1 Свойства сложения и вычитания
- § 2 Упрощение выражений
§ 1 Свойства сложения и вычитания
В этом уроке Вы познакомитесь с буквенной записью различных свойств сложения и вычитания, кроме того узнаете, как можно упростить числовое или буквенное выражение, используя эти свойства.
Все свойства сложения и вычитания можно записать с помощью букв, т.е. в виде буквенных выражений.
1. Переместительное свойство сложения, которое звучит следующим образом: При перестановке слагаемых сумма не меняется.
Можно записать так: а + b = b + а
В этом равенстве буквы а и b могут принимать любые натуральные значения и значение ноль тоже.
2. Сочетательное свойство сложения:
Чтобы к числу прибавить сумму двух чисел, можно к этому числу сначала прибавить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое.
Данное свойство с помощью букв записывается таким образом:
a + (b + c) = (a + b) + c = а + b + с
Здесь а, b, с также могут принимать любые натуральные значения и ноль.
3. Свойство нуля при сложении.
Если к числу прибавить ноль, то получится само число. Если к нулю прибавить какое- либо число, то получится прибавленное число.
С помощью букв это свойство можно записать таким образом a + 0 = 0 + a = а.
И здесь буква а может принимать любое значение.
4. Свойство вычитания суммы из числа.
Чтобы вычесть сумму двух чисел из данного натурального числа, необходимо сначала вычесть из этого числа первое слагаемое, а потом из полученной разности – второе слагаемое.
Данное свойство с помощью букв записывается следующим образом:
а – (b + с) = а – b – с
Здесь обязательно должно выполняться условие, что сумма в + с меньше или равна а. Данная запись выглядит так: b + с < а или b + с = а
5. Свойство вычитания числа из суммы.
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое.
Здесь важно учесть, что вычитаемое должно быть меньше слагаемого, из которого его вычитают, или равно ему.
С помощью букв это свойство записывается так:
(а + b) – с = (а – с) + b, если с < а или с = а
Или же
(а + b) – с = а + (b – с), если с < b или с = b
6. Свойства нуля при вычитании.
Если из числа вычесть нуль, оно не изменится.
Соответствующее буквенное выражение будет выглядеть так: а – 0 = а
7. Свойства нуля при вычитании.
Если из числа вычесть число, равное ему, то получится ноль.
а – а = 0
В этих двух выражениях буква а может принимать любые натуральные значения и значение ноль.
§ 2 Упрощение выражений
Давайте выполним несколько заданий, используя буквенную запись свойств сложения и вычитания.
Задание №1:
Запишите сочетательное свойство сложения с помощью букв х, у, с.
Замените буквы их значениями х = 12, у = 18, с = 20 и проверьте получившееся числовое равенство.
Решение:
Сочетательное свойство сложения звучит следующим образом: чтобы к числу прибавить сумму двух чисел, можно к этому числу сначала прибавить первое слагаемое, а затем к полученной сумме прибавить второе слагаемое.
С помощью букв х, у и с, можем записать его в виде: х + (у + c) = (х + у) + c.
Теперь проверим данное равенство, подставив вместо х число 12, вместо у число 18, вместо с число 20, получаем следующую запись:
12 + (18 + 20) = (12 + 18) + 20
Проверим ее: в левой части равенства сумма 18 и 20 равна 38, прибавив к 12 тридцать восемь получим 50.
Теперь вычислим правую часть равенства: 12 + 18 равно 30, затем 30 + 20 получится 50. Т.е. равенство верное.
Задание №2:
Упростите выражение 137 – с – 27.
Решение:
Представим данное выражение в виде: 137 – (с+27).
С помощью переместительного свойства сложения перепишем равенство в виде:
137 –(27+с)
Теперь с помощью свойства вычитания суммы из числа, имеем:
137-c-27=137-(c+27)=137-(27+c)=137-27-c=110-c
Таким образом, на этом уроке Вы познакомились с буквенной записью свойств сложения и вычитания, а также узнали, как можно упростить числовое или буквенное выражение, используя эти свойства.
Список использованной литературы:
- Математика 5 класс. Виленкин Н.Я., Жохов В.И. и др. 31-е изд., стер. – М: 2013.
- Дидактические материалы по математике 5 класс. Автор – Попов М.А. – 2013.
- Вычисляем без ошибок. Работы с самопроверкой по математике 5-6 классы. Автор – Минаева С.С. – 2014.
- Дидактические материалы по математике 5 класс. Авторы: Дорофеев Г.В., Кузнецова Л.В. – 2010.
- Контрольные и самостоятельные работы по математике 5 класс. Авторы – Попов М.А. – 2012 год
- Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений / И. И. Зубарева, А. Г. Мордкович. — 9-е изд., стер. — М.: Мнемозина, 2009.
Источник
