Какие бывают свойства сложения 4 класс

математика 4 класс, урок 19 (ч.1.с. 40-41)
Дата:
Тема: Свойства сложения.
Педагогические цели: знакомство с обозначением чисел буквами.
Планируемые результаты образования:
Предметные: знакомство с обозначением чисел буквами; повторить переместительное и сочетательное свойство сложения, сложение с числом 0; нахождение неизвестного сложения и вычитания; решение задач на определение пути. Выполнять сложение и вычитание многозначных чисел.
Личностные: самооценка своей работы.
Метапредметные (критерии сформированности/оценки компонентов УУД):
Регулятивные: обозначением чисел буквами; использовать переместительное и сочетательное свойство сложения, сложение с числом 0; находить неизвестное сложение и вычитание; решение задач на определение пути. Выполнять сложение и вычитание многозначных чисел.
Познавательные: обозначением чисел буквами
Коммуникативные: слушают , рассуждают, доказывают свои предположения.
Образовательные ресурсы: электронный учебник.
Технологическая карта урока №19
Основные этапы организации учебной деятельности
Содержание педагогического взаимодействия
Деятельность учителя
Деятельность обучающихся
Мотивирование к учебной деятельности (организационный момент).
Дыхательная разминка.
Запись числа.
Чистописание.
Актуализация и фиксирование индивидуального затруднения в пробном учебном действии.
1.Устный счет
А) Назовите число, расположите в порядке возрастания:
8сот.2дес. 6сот.9дес.6ед. 2сот. 5ед. 5сот.
Б) Вставь пропущенные числа.
* х 2 = 10 150 + * = 200
* + 350 = 1350 2 400 – * = 2 150
В) Вставь пропущенные числа и знаки действий так, чтобы вы смогли найти значение полученного выражения.
3 1 4 2
*…(* … *) …* …*
Выполняют вычисления:
250, 500, 696, 820
5х2=10 150+50=200
1000+350=1350 2 400-250=2150
20 + (5 + 5)-4 х 2
Постановка учебной задачи.
Определите тему урока. Поставьте учебные задачи.
Открытие нового знания (построение проекта выхода из затруднения).
№1
Какое свойство сложения записано с помощью схемы?
+ = +
Математики часто обозначают числа не знаками, а латинскими буквами. Латинский алфавит вы найдёте на форзаце в конце учебника.
– Рассмотрите таблицу, что вам уже известно, а в чем вызвано затруднение.
№2
– В каждом столбике найдите суммы с одинаковым значением.
№1
С помощью схемы записано переместительное свойство сложения.
№2
35 821+18 674 634 578+136 790 445698+2395
Первичное закрепление.
№3
– Рассмотрите выражение (a+500)+b. Вместо букв можно подставить разные числа. При этом будут получаться разные значения выражения.
Поставь вместо букв числа и запиши получившиеся выражения.
Найди значения получившихся выражений удобным способом.
Какие законы сложения вы использовали при вычислениях?
№3
(13 876+500)+1500
(27500+500)+2370
(1900+500)+100
Самостоятельная работа с самопроверкой по образцу (эталону).
№4
Неизвестное число в равенстве также часто обозначают латинской буквой.
Найдите неизвестное число и сделай проверку.
№4
Х=49 520
У=28 700
И=59 750
С=137 390
Включение нового знания в систему знаний и повторение.
№6
Используйте свои знания в задаче.
№7
– Вычислите.
ЗАДАНИЯ ПО ВЫБОРУ:
№8
№9
№6
1)76х5=350(км)-проехал поезд
2)730-380=350(км)-осталось проехать
Ответ: 350 км-меньше половины пути.
№7
528 631; 1 784 720;
4 845 5654; 93 718.
№8
Ответ: автобус проходит на 36 км больше.
№9
В) подставить можно, но посчитать нельзя, т.к. b-с=60-100
Рефлексия учебной деятельности на уроке (итог).
Какую задачу ставили на уроке?
– Удалось решить поставленную задачу?
– Каким способом?
– Какие получили результаты?
– Что нужно сделать еще?
– Где можно применить новые знания?
– Что на уроке у вас хорошо получилось?
– Над чем еще надо поработать?
д/з
№5
Источник
Тема урока: «Свойства сложения».
Цель: обучающая – выявить и обосновать особенность переместительного и сочетательного
свойства сложения и умножения;
развивающая – развивать логическое мышление, речь;
воспитательная – содействие воспитанию самостоятельности, познавательной активности.
Тип: урок изучения нового материала.
Форма: урок – практикум.
Технология: информационно-коммуникационная, личностно – ориентированного обучения.
Методы: словесный, наглядный, частично-поисковый, исследовательский, практический,
Оборудование: индивидуальные карточки с разноуровневым заданием, компетентностно –
ориентированные задания.
ТСО: компьютер, презентация по теме.
Межпредметная связь: с алгеброй.
Мотивация посредством решения заданий многоуровневого характера.
Применение знаний при выполнении практических работ, разноуровневых заданий.
I. Организационный момент. Психологический настрой.
– Личная цель каждого ученика на урок.
II. Проверка домашнего задания.
Обосновать правильность и рациональность способов решение задачи №5 стр.283
(учебник «Математика» для 4 класса).
III. Повторение изученного.
«Интеллектуальная разминка». Математический диктант. (1 чел. у доски)
Приложение №1
IV. Актуализация новой темы.
Объяснение новой темы учеником.
Выполнение компетентностно – ориентированное задание.
(Приложение. №2)
Работа по учебнику. (стр.284)
– Рассмотрите объяснение темы, данное в учебнике и сделайте вывод.
V. Закрепление изученного материала.
1. Комментированное решение примеров, уравнений. №2,3 стр.285
2. Упражнение «Заморочки»:
Решение заданий на выбор с объяснением. № 6 или № 8 стр.285
Упражнение «Эксперимент»:
Реши задачу, используя рисунок к задаче: В трех ящиках 723 кг яблок. В первом ящике
240 кг, это в 2 раза больше, чем во втором ящике. Сколько килограммов яблок в третьем ящике?
VI. Оперативный контроль.
1) Самостоятельная работа (Работа в группах)
1 группа (весь класс) Решение задачи. № 9 стр.286
2 группа (инд. опрос по карточкам у доски):
1 ученик. Упражнение «Рассуждение».
2 ученик. Упражнение «Ловушка».
Приложение №3.
2) Проверка выполнения самостоятельной работы.
VII. Домашнее задание.
Решение уравнений №4, задачи №7 стр. 285
VIII. Рефлексия.
ПРИЛОЖЕНИЕ №1
Математический диктант.
1. Запиши цифрами и подчеркни одной чертой класс единиц, двумя – класс тысяч тремя – класс
миллионов: 3.007.009; 9.050; 20.700.000;
2. Запиши и разложи число на разрядные слагаемые: 9.000.005.20
3. Запиши и найди сумму трёх слагаемых, из которых первое – 2 миллиона, а каждое следующее
на 100 больше (Ответ: 2.000.000 + 2.000.100 +2.000.200 = 6.000.300)
4. Разложи число на удобные слагаемые (или 1 или 2 слагаемое разложить):
86 + 38 = (Например, 86 +(4 + 34) = 124)
5. Разложи число на удобные множители ( или 1 или 2 множитель разложить):
35· 18 = (Например, 35 · (2 · 9) = 630)
6. Делимое 1000, делитель 100, найди частное. (10)
7. Первый множитель 120, произведение 2400, найди второй множитель. (20)
8. Уменьши 120 на 60. (60)
9. Размах крыльев у кондора 275см. Сколько это …м … дм …см? (2м 7дм 5см)
10. Ширина дороги 15 м, а длина 3км. Какую площадь занимает дорога? (45000 м2)
ПРИЛОЖЕНИЕ №2
Компетентностно – ориентированное задание.
Выполни исследование и ответь на проблемный вопрос.
– В чем отличие переместительного от сочетательного свойства сложения и умножения?
Модель рассуждения.
Пошаговая инструкция:
Рассмотри нахождение значения суммы.
28 = 97 + (3+25) = (97 + 3) + 25 = 100 + 25 = 125
Рассмотри нахождение значения произведения.
25 · 16 = 25 · (4 ·4) = (25 · 4) · 4 = 100 · 4 = 400
Поиск информации:
Провести поиск нахождение значений сумм и произведений в учебнике «Математика» для
4 класса (стр. 284)
Продукт деятельности. Защита работы.
Прием рассуждение. Аргументирование.
ПРИЛОЖЕНИЕ №3
Карточки для индивидуального опросы.
Карточка. 1 Упражнение «Рассуждение».
Задание. Начерти схему к задаче. Составь и реши задачу на противоположное
движение, используя данные величины: 17 км/ч, 4 часа, 496 км, ? км/ч
Карточка. 2 Упражнение «Ловушка».
Длина прямоугольника 29 см, периметр 84 см. Найти ширину прямоугольника.
Источник

Базовые свойства
Главными элементами сложения являются аргументы (слагаемые). Сумма — результат увеличения значений первого и второго аргументов. На письме эта математическая операция обозначается символом +. Основными свойствами сложения в математике являются:


- Коммутативность: от изменения мест слагаемых сумма не меняется. Это правило также называется переместительным свойством сложения. В буквенном виде коммутативный закон записывается следующим образом: a + b = b + a. Чаще всего он применяется при решении простых уравнений и неравенств.
- Ассоциативность: порядок действия не влияет на результат сложения трех и более слагаемых. Называется это правило сочетательным свойством сложения. Ассоциативный закон применяется при группировке или перестановке слагаемых. Буквенная запись сочетательного закона выглядит следующим образом: a + b + c = a + (b + c).
- Дистрибутивность: 2 бинарные операции, определенные на одинаковом множестве, всегда находятся в согласованности. В математике это правило именуется распределительным свойством сложения.
- Нейтральный элемент: если к первому компоненту сложения прибавить нуль, то сумма будет равна исходному числу. В буквенном виде этот закон записывается так: a + 0 = a. Свойство нейтрального элемента является одним из старейших правил сложения в математике. Оно было сформировано во второй половине VII века в «Исправленном трактате Брахмы».
- Обратный элемент: при сложении чисел с одинаковым значением, но разными знаками сумма равна нулю. В буквенном выражении этот математический закон выглядит следующим образом: a + (- a) = 0.
Базовые свойства сложения изучаются в начальной школе со 2 класса. Процесс обучения начинается с простых заданий с двумя компонентами, представленными натуральными числами. По мере обучения увеличивается сложность задач и количество слагаемых. В школе большинство вычислений производится в десятичной системе счисления, поэтому в качестве памятки рекомендуется предоставить ученикам таблицу сложения, где представлены суммы пар чисел от 1 до 10.
Нахождение суммы многозначных чисел
Многозначными называются числа, состоящие из двух и более цифр. Для нахождения их суммы необходимо знание численных разрядов. Цифра, стоящая последней, показывает количество единиц. Далее идут десятки, сотни, тысячи, десятки тысяч, сотни тысяч и миллионы. Многозначные числа складываются столбиком. Сложить можно только одинаковые разряды.
Пример: найти сумму многозначных чисел 125 и 234. Отдельно складываются единицы, десятки и сотни: 5 + 4 = 9, 2 + 3 = 5, 1 + 2 = 3. Суммой является число 359.

Для проверки правильности вычислений нужно вычесть из суммы одно из слагаемых. Если разность равна второму слагаемому, то пример решен правильно. Проверку можно осуществить также при помощи калькулятора или иных вычислительных устройств.
Прибавление дробей и смешанных значений
Дробь — часть от целого числа, записываемая в виде x / y. Значение x называется числителем, y — знаменателем. Дробное число представляет собой операцию деления, где делимым является числитель, а делителем — знаменатель. Дробь считается правильной, если числитель не больше знаменателя.
При складывании дробей с одинаковыми знаменателями необходимо прибавлять только их числители (например, 1/5 + 3/5 = 4/5). Если значения, стоящие под знаком дроби, разные, то необходимо привести выражение к единому знаменателю:

- Найти наименьшее общее кратное для исходных знаменателей дробей.
- Определить дополнительные множители для числителей (наименьшее общее кратное поделить на знаменатели).
- Найти произведение числителей на дополнительные множители.
- Сложить получившиеся дроби с одинаковым знаменателем.
Для упрощения этой процедуры рекомендуется приобрести таблицу умножения. С ее помощью можно легко найти общий знаменатель и дополнительные множители.
Десятичной называется дробь, знаменатель которой равен 10. Она состоит из целой и дробной частей, отделенных запятой. При нахождении суммы десятичные дроби записываются столбиком. Важно, чтобы запятые находились на одном уровне. При неравном количестве разрядов с правой стороны дописываются нули. Если в результате после запятой стоит 0, то он опускается.

Смешанное число — сумма обыкновенной дроби (дробная часть) и целого числа (целая часть).
Для определения суммы чисел в смешанной записи необходимо отделить целую часть от дроби и сложить их по отдельности, применяя базовые свойства сложения. Если в результате вычислений получилась неправильная дробь, то нужно следовать следующему алгоритму действий:
- Найти произведение знаменателя и целой части смешанного числа.
- Прибавить к получившемуся числу числитель дробной части.
- Результат измерений записать в качестве числителя, а число, стоящее под знаком дроби, оставить без изменений.
В математике процесс преобразования неправильной дроби в смешанное число называется выделением целой части. Если числитель полностью делится на знаменатель, то неправильную дробь можно записать в виде целого числа.
Складывание векторов, пределов и матриц
Вектор — отрезок, имеющий длину и направление. Он является одним из основополагающих понятий линейной алгебры. В буквенном виде он записывается двумя заглавными символами латинского алфавита или одной маленькой латинской буквой. Существует два основных способа сложения векторов:
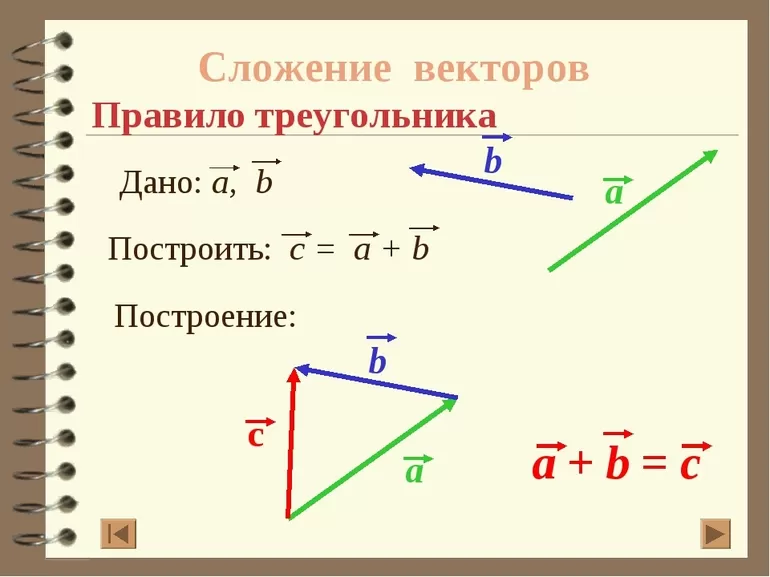
- Метод треугольников: на плоскости необходимо отметить произвольную точку и отложить от нее первый вектор. От конца первого отрезка откладывается второй. Начало первого вектора и конец второго нужно соединить. Полученный отрезок является их суммой. Этот способ используется только для нахождения суммы коллинеарных векторов, не лежащих на параллельных прямых.
- Правило параллелограмма: нужно отметить на плоскости произвольную точку и отложить от нее оба вектора. Фигура достраивается до параллелограмма. Диагональ этого многоугольника является суммой векторов.
Для нахождения суммы трех и более векторов необходимо отметить на плоскости произвольную точку и последовательно отложить от нее исходные векторы. Отрезок, соединяющий начало первого вектора и конец последнего, является суммой. При сложении важно учитывать, что результат сложения противоположно направленных векторов равен 0. Наглядно способы нахождения суммы векторов проиллюстрированы ниже.
Пределом функции является число, к которой стремится значение функции f (x) при стремлении ее аргумента к заданной точке на графике. Является одним из разделов математического анализа. Предел функции вычисляется по следующей формуле: limx →∞ f (x)= C, где C — число, к которому стремится аргумент функции. Для нахождения предела суммы необходимо сложить функции, стремящиеся к идентичным точкам на заданном графике.

Матрица — элемент высшей математики, представленный в виде таблицы прямоугольной формы. Она состоит из неограниченного количества строк и столбцов, где записываются целые, действительные, иррациональные и комплексные числа. В квадратных матрицах количество столбцов и строк совпадает. Нулевой называется таблица, где все компоненты равны 0. Матрицы нашли применение в записи алгебраических и дифференциальных уравнений.
Складывать можно только одноразмерные матрицы (число строк и столбцов совпадает). В противном случае может измениться их исходный размер. При нахождении суммы матриц каждые элементы складываются по отдельности. Нельзя сложить компоненты, находящиеся в разных строках или столбцах. В результате получится матрица с исходным размером. При сложении применяются свойства коммутативности и ассоциативности. Для складывания нулевых матриц важно знать правило нейтрального элемента.
Сложение в двоичной системе счисления
В двоичной системе счисления математические операции выполняются на электронно-вычислительных машинах. В ней применяются только две цифры: 0 и 1. Сложение в этой системе счисления выполняется в столбик. Для вычислений требуется следующая таблица:

| Условие математической операции |
| 0 + 0 = 0 |
| 0 + 1 = 1 |
| 1 + 0 = 1 |
| 1 + 1 = 10 |
Числа, записываемые в столбик, выравниваются по разделителю целой и дробной частей. Если количество разрядов не совпадает, то с правой стороны необходимо добавить нули. При складывании нескольких чисел возможен перенос через 2 и более разряда.
Для упрощения математической операции можно перевести числа из двоичной системы счисления в десятичную. Для этого над каждой цифрой исходного числа слева направо ставится степень, начиная от 0. Каждый элемент умножается на цифру 2, возведенную в соответствующую степень. Результаты вычислений суммируются. С помощью этого способа можно также переводить в восьмеричную и шестнадцатеричную системы счисления.
Источник
Предложенная разработка урока математики в 4 классе по теме «Переместительное и сочетательное свойства сложения и умножения», представила опыт работы педагога по повышению качества начального образования посредством использования деятельностных технологий как основа компетентностного обучения. Использование заданий многоуровневого характера в виде компетентностно–ориентированных заданий, упражнений типа «Заморочки», «Эксперимент», «Рассуждение», «Ловушка», активных форм организации учебного процесса «Практикум» и методов взаимодействия, обеспечивает формирование предметной компетентности как фактор личностного саморазвития и самоопределения младшего школьника.
Цель:
1.обучающая: выявить и обосновать особенность переместительного и сочетательного
свойства сложения и умножения;
2.развивающая: развивать логическое мышление, речь;
3.воспитательная: содействие воспитанию самостоятельности, познавательной активности.
Тип: урок изучения нового материала.
Форма: урок – практикум.
Технология: информационно-коммуникационная, личностно – ориентированного обучения.
Методы: словесный, наглядный, частично-поисковый, исследовательский, практический.
Оборудование: индивидуальные карточки с разноуровневым заданием, компетентностно –
ориентированные задания.
ТСО: компьютер, презентация по теме.
Межпредметная связь: с алгеброй.
Мотивация посредством решения заданий многоуровневого характера.
Применение знаний при выполнении практических работ, разноуровневых заданий.
“ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
I. Организационный момент. Психологический настрой.
– Личная цель каждого ученика на урок.
II. Проверка домашнего задания.
Обосновать правильность и рациональность способов решение задачи №5 стр.283
(учебник «Математика» для 4 класса).
III. Повторение изученного.
«Интеллектуальная разминка». Математический диктант. (1 чел. у доски)
Приложение №1
IV. Актуализация новой темы.
1. Объяснение новой темы учеником.
Выполнение компетентностно – ориентированное задание.
(Приложение. №2)
2. Работа по учебнику. (стр.284)
– Рассмотрите объяснение темы, данное в учебнике и сделайте вывод.
V. Закрепление изученного материала.
1. Комментированное решение примеров, уравнений. №2,3 стр.285
2. Упражнение «Заморочки»:
Решение заданий на выбор с объяснением. № 6 или № 8 стр.285
3. Упражнение «Эксперимент»:
Реши задачу, используя рисунок к задаче: В трех ящиках 723 кг яблок. В первом ящике
240 кг, это в 2 раза больше, чем во втором ящике. Сколько килограммов яблок в третьем ящике?
VI. Оперативный контроль.
1) Самостоятельная работа (Работа в группах)
1 группа (весь класс)
Решение задачи. № 9 стр.286
2 группа (инд. опрос по карточкам у доски):
1 ученик.
Упражнение «Рассуждение».
2 ученик.
Упражнение «Ловушка».
Приложение №3.
2) Проверка выполнения самостоятельной работы.
VII. Домашнее задание.
Решение уравнений №4, задачи №7 стр. 285
VIII. Рефлексия.
ПРИЛОЖЕНИЕ №1
Математический диктант.
1. Запиши цифрами и подчеркни одной чертой класс единиц, двумя – класс тысяч тремя – класс
миллионов: 3.007.009; 9.050; 20.700.000;
2. Запиши и разложи число на разрядные слагаемые: 9.000.005.20
3. Запиши и найди сумму трёх слагаемых, из которых первое – 2 миллиона, а каждое следующее
на 100 больше (Ответ: 2.000.000 + 2.000.100 +2.000.200 = 6.000.300)
4. Разложи число на удобные слагаемые (или 1 или 2 слагаемое разложить):
86 + 38 = (Например, 86 +(4 + 34) = 124)
5. Разложи число на удобные множители ( или 1 или 2 множитель разложить):
35· 18 = (Например, 35 · (2 · 9) = 630)
6. Делимое 1000, делитель 100, найди частное. (10)
7. Первый множитель 120, произведение 2400, найди второй множитель. (20)
8. Уменьши 120 на 60. (60)
9. Размах крыльев у кондора 275см. Сколько это …м … дм …см? (2м 7дм 5см)
10. Ширина дороги 15 м, а длина 3км. Какую площадь занимает дорога? (45000 м2)
ПРИЛОЖЕНИЕ №2
Компетентностно – ориентированное задание.
Выполни исследование и ответь на проблемный вопрос.
– В чем отличие переместительного от сочетательного свойства сложения и умножения?
Модель рассуждения.
Пошаговая инструкция:
Рассмотри нахождение значения суммы.
28 = 97 + (3+25) = (97 + 3) + 25 = 100 + 25 = 125
Рассмотри нахождение значения произведения.
25 · 16 = 25 · (4 ·4) = (25 · 4) · 4 = 100 · 4 = 400
Поиск информации:
Провести поиск нахождение значений сумм и произведений в учебнике «Математика» для
4 класса (стр. 284)
Продукт деятельности. Защита работы.
Прием рассуждение. Аргументирование.
ПРИЛОЖЕНИЕ №3
Карточки для индивидуального опросы.
Карточка. 1 Упражнение «Рассуждение».
Задание. Начерти схему к задаче. Составь и реши задачу на противоположное
движение, используя данные величины: 17 км/ч, 4 часа, 496 км, ? км/ч
Карточка. 2 Упражнение «Ловушка».
Длина прямоугольника 29 см, периметр 84 см. Найти ширину прямоугольника.
Источник
