Какая величина определяет резонансные свойства контура
Последовательное соединения элементов R, L, C называется последовательным колебательным контуром, в нем возможен резонанс напряжения. Резонансом напряжения называется такой режим в колебательном контуре, при котором частота источника э.д.с. равна частоте собственных колебании контура
Выходное напряжения u=
1.При резонансе напряжения, входное сопротивление становится чисто резистивным, реактивное входное сопротивление становится число резистивным, реактивное входное сопротивление равно нулю
Ẕ=R+j , Ẕ=R.
2.резонансная частота контура определяется из соотношения т.е.
3.Так как = + , X=0, Z=R.полное сопротивление минимально, тогда токи в цепи и активная мощность в режиме резонанса максимальны P= .
4. U= Напряжения на реактивных элементах равны величине и противоположны по направлению. Реактивное мощности тоже равны
5. характеристическое или волновое сопротивление контура.
6. Отношение напряжении на реактивных элементах к приложенному напряжению, или отношение реактивных мощностей к активной мощности в режиме резонанса называется добротностью контура
-добротность контура.
Добротность контура указывает во сколько раз напряжение на индуктивности и емкости при резонансе больше, чем напряжение приложенное к цепи. Добротность обычных контуров бывает порядка от 50 до 300. Это означает, что напряжение и мощность реактивных элементов в десятки и в сотни раз превышает напряжение и мощность источника. Векторная диаграмма в момент резонанса.
Параллельное соединение элементов R,L,C называется параллельным колебательным контуром, в нем возможен резонанс токов. Резонанс токов наступает, когда выходная проводимость реактивная равна нулю.
……………………
Ток в неразветвленной части: ḻ= где Y-входная комплексная проводимость.
Y=G-j При резонансе токов B=0? резонансная частота контура.
При резонансе U⦁ ток через индуктивный элемент равен по модулю току через емкостный элемент и находится в противофазе и могут превышать входной ток.
Добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.
Ǫ= добротность параллельного контура, показывает во сколько раз ток в реактивных элементах при резонансе больше тока на входе контура.
Частотные характеристики параллельного колебательного контура.
Частотное характеристики резонансных контуров.
Пусть к цепи пртложенно синусоидальное напряжение амплитуда которого постоянна, а частота изменяется от изменение частоту проводит к изменению параметров цепи. Меняется реактивное сопротивление, полное сопротивление, а также уголь Зависимость действующих или амплитудных значений тока I и напряжении от частоты называется резонансными кривыми.
= X( )= называется частотным характеристиками цепи, а зависимости I( ), называется резонансными кривыми.
……………………………
Для удобства сравнения резонансных кривых друг с другом будем рассматривать зависимости: где ток при резонансе, -резонансное частота.
.
Чем больше Ǫ, тем острее резонансная кривая, тем лучше избирательные свойства цепи.
……………………
Вопросы для самоконтроля:
1. Условия для наступления в цепи резонанса напряжении.
2. Чему равно входное сопротивление цепи в момент резонанса.
3. Векторная диаграмма цепи в момент резонанса
4. Добротность контура. Применение явления резонанса.
5. Условия резонанса тока.
6. Частотные характеристики последовательно колебательного контура.
7. Полоса пропускания контура и ее связь с добротностью контура.
Литература:
1.Атабеков Г.И. Основы теории цепей.-М.: Энергия, 2006-544с.
2.бакалов В.П., Воробинко П.П. Крук Б.И Теория электрических цепей.-М.: Радио и связь, 1998-440с.
3.Под редакцией Ионкина П.Теоритические основы электротехники. М.:
Высшая школа.1976-545с.
4.Зевеке Г.В Ионкин П.А и др. Основы теории цепей. М.:Энергия, 1989-528с.
Планы практических занятий
Тема №1.Эквивалентное преобразования электрических цепей. Преобразование треугольника сопротивлений в звезду сопротивлении. Определении эквивалентных сопротивлении
Повторить эквивалентные преобразования простейших резистивных цепей: последовательное, параллельное, смешанное соединение цепей. Изучить преобразование треугольника сопротивление в звезду. Формулы преобразование. Закрепить и уметь применять эквивалентные преобразования при решении практических задач.
Задания: Изучить эквивалентные преобразование электрических цепей.
Уметь рассчитывать эквивалентные сопротивления цепей. Преобразование треугольника сопротивлении в звезду. Уметь преобразовывать сложные электрические цепи в простые в помощью эквивалентных преобразований.
Решение задач 1.2, 1.3, 1.8, 1.10, 1.50 Л [1]
Основные вопросы:
Определить эквивалентное сопротивление трех параллельно соединенных резисторов. Получить формулу «разброса» для нахождения токов в параллельных ветвях. Рассчитать цепь при смешанном соединении резисторов.
Методические рекомендации к выполнению:
Изучить эквивалентные преобразования «треугольника» сопротивлений в звезду. Вспомнить простейшие эквивалентные преобразования: последовательное, параллельное, смешанное соединение цепей.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема№2.Преобразование звезды сопротивление в треугольник сопротивлений. Источники э.д.с. и тока. Эквивалентные преобразование источников.
Цели занятия:
Рассмотреть и закрепить преобразование «звезды» сопротивлений в треугольник сопротивлений. Рассмотреть эквивалентные преобразование источников. Закрепить и уметь применить знания при решении практических задач.
Задания: Решить задачи 1.51, 1.52, 1.53, 1.54, 1.55, 1.56, 1.58,1.59 Л[1].
Основные вопросы:
Особенности преобразования звезды сопротивлений в треугольник.
Эквивалентные преобразование источника тока в источник э.д.с..
Эквивалентные преобразование источника э.д.с. в источник тока.
Методические указания к выполнению:
Изучить эквивалентные преобразования сопротивлений по схеме «звезда» в треугольник. Вспомнить простейшие эквивалентные преобразования: последовательное, параллельное, смешанное соединение цепей.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема№3.Электрические цепи гармонического тока. Определение эквивалентных комплексных сопротивлений. Алгебраическая и показательная формы. Треугольник проводимостей.
Цель занятия:
Рассмотреть и закрепить электрические цепи гармонические тока. Уметь определять выражение комплексного сопротивления и комплексной проводимости, модуль, аргумент. Уметь работать с комплексными числами, производить действия с комплексными числами уметь переходить из показательной формы в алгебраическую, из алгебраической в показательную. Изучить законы Ома и Кирхгофа в комплексной форме.
Задания:Решить задачи 2.2, 2.3, 2.4, 2.5, 2.8, 2.18, 2.19,2.24, 2.30, 2.32, 2.34 Л[1].
Основные вопросы:
Изображения синусоидальной функции вращающимся вектором.
Изображения синусоидальной функции комплексным числом.
Полное, активное и реактивное сопротивление. Треугольник сопротивлений.
Полная, активная и реактивная проводимость. Треугольник проводимостей.
Методические указания к выполнению:
Изучить и закрепить особенности гармонического тока. Решить задачи для закрепления данного материала. Уметь определить комплексное, полное, активное и реактивное сопротивление. Уметь определять комплексную, полную, активную, реактивную проводимость. Аргумент комплексного сопротивления. Рассмотреть законы Ома и Киргхгофа в комплексной форме.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №4.Методы представления гармонических функций. Символический метод. Пассивные элементы гармонического тока. Векторная диаграмма. Топографическая диаграмма. Измерение мощностей.
Цель занятия:
Рассмотреть методы представления гармонической функции.
Представление гармонической функции графиком во временной области. Изображение гармонической функции вращающимся вектором. Изображение гармонической функции комплексным числом. Изучить построение векторных и топографических диаграмм. Рассмтреть измерение мощностей в цепи гармонического тока.
Задания:Решение задачи 2.43, 2.48 2.49, 2.50, 2.51, 2.52, 2.53 Л[1].
Основные вопросы:
Рассмотреть методы представления гармонических функций.
Методы расчета цепей гармонического тока в комплексной форме. Символический метод. Векторные диаграммы отдельных элементов, векторные диаграммы отдельных электрических цепей. Топографические диаграммы. Измерение мощности ваттметром.
Методические указания к выполнению:
Изучить методы расчета цепей гармонического тока. Особенности применения методов расчета постоянного тока для решения задач гармонического тока.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №5.Частотные характеристики электрических цепей. Комплексные передаточные функции линейных электрических цепей. Частотные характеристики последовательного колебательного контура. Частотные характеристики параллельного колебательного контура.
Цель занятия:Изучить комплексные передаточные характеристики электрических цепей: комплексную передаточную функцию по току, комплексное передаточное сопротивление и комплексная передаточная проводимость. Изучить построение амплитудно-частотную и фаза – частотных характеристик. Изучить и закрепить частотные характеристики резонансные колебательного контура.
Занятия:Построить амплитудно-частотную и фазо – частотную характеристики комплексной передаточной функцию по напряжению последовательного колебательного контура для различных значении добротности, изменяя частоту в пределах 0.25 до 2 .
Построить амплитудно-частотную и фаза – частотную характеристики комплексной передаточной функцию по току параллельного колебательного контура изменяя частоту в пределах 0.25 до 2 , для различных значений добротности.
Методические рекомендации к выполнению:
Изучить частотные характеристики электрических цепей, уделив особое внимание на построение амплитудно-частотную и фаза – частотную характеристик.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №6Частотные характеристики реактивных двухполюсников,
Цель занятия:
Изучить и закрепить общие свойства реактивных двухполюсников. Изучить частотные зависимости входных функции цепи: входного комплексного сопротивления и входной комплексной проводимости. Изучить канонические схемы реактивных двухполюсников.
Задание:Построить зависимости входных функций от частоты простых двухполюсников, состоящий из одного элемента: одного индуктивного и одного емкостного элемента(одноэлементные двухполюсники).
Построить функции входного сопротивления и входной проводимости двухэлементных двухполюсников.
Построить функции входного сопротивления и проводимости трехэлементных двухполюсников.
Методические рекомендации к выполнению:
Изучить и закрепить частотные характеристики реактивных двухполюсников.
Уметь строить зависимости входных функции от частоты.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №7.Особенности анализа индуктивно связанных элементов. Расчет по законам Кирхгофа. Метод контурных токов. Воздушный трансформатор.
Цель занятия:
Изучить и закрепить основные методы анализа цепей с индуктивно связанными элементами. Изучить особенности явлений, происходящих в электрических цепях с индуктивно связанными элементами. Уметь определять коэффициент взаимной индукции, составлять уравнения равновесия, уметь определять одноименные зажимы и построения векторных диаграмм.
Задания.Изучить методы анализа цепей с индуктивными связями: расчет по законом Кирхгофа и метод контурных токов. Изучить особенности анализа этих цепей. Изучить методы развязки индуктивно связанных цепей. Изучить частотные характеристики связанных колебательных контуров.Построить амплитудно-частотную характеристику связанных колебательных контуров.
Методические рекомендации к выполнению:
Изучить и закрепить особенности индуктивно связанных цепей. Уметь применять законы Кирхгофа, метод контурных тоов. Для инфуктивно связанных цепей подходят только эти методы расчета.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Тема №8.Методы расчета и измерение мощностей в трехфазных цепях.
Цель занятия:
Закрепить методы симметричных и несимметрических трехфазных цепей. Закрепить особенности методы симметричных составляющих для расчета несимметрических трехфазных цепей. Изучить свойство трехфазных цепей в отношении симметричных составляющих токов и напряжений. Изучить методы измерения мощности в трехфазных цепях.
Задания:
Произвести расчет трехфазной цепи при поперечной несимметрий.
Произвести расчет трехфазной цепи при продольной несимметрии.
Произвести расчет мощности трехфазной цепях.
Методические рекомендации к выполнению:
Изучить методы анализ симметричных и несимметрических трехфазных цепей.
Изучить метод симметрических составляющих для решения несимметричных режимов в трехфазных цепях.
Литература:
1. Шебес М.Р., Каблукова М.В. Задачник по теории электрических цепей. – М.: Высшая школа, 1990. – 544с.
2. Атабеков Г.И. Основы теории цепей. –М.: Энергия, 2006.- 540с.
3. Бакалов В.П., Воробиенко П.П. Теория электрических цепей. – М.: Радио и связь, 1998.- 440с.
4. Зевеке Г.В., Ионкин П.А., и др. Основы теории цепей.М.: Энергия, 1989.-528с.
Дата добавления: 2016-03-27; просмотров: 906 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org – Контакты – Последнее добавление
Источник
Если предварительно зарядить конденсатор и подключить его к индуктивности (рис. 4.2.7.1), то будет происходить обмен энергией между электрическим полем конденсатора и магнитным полем катушки. В этой цепи будут происходить колебания, поэтому этот контур называется колебательным.
Рис.4.2.7.1.
Так как колебания происходят без воздействия внешнего источника, а за счет заранее занесенной энергии, то они называются свободными.
Колебания происходят с определенной частотой , называемой частотой свободных колебаний.
Из условия равенства энергий
= ; ;
Основными параметрами колебательного контура, кроме частоты свободных колебаний, являются:
– период свободных колебаний:
;
– характеристическое (волновое) сопротивление:
Характеристическим сопротивлением называется индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний.
Так как в контуре отсутствуют потери, то контур называется идеальным.
В реальном колебательном контуре (рис. 4.2.7.2) имеются потери, поэтому при возникновении в контуре свободных колебаний энергия предварительно заряженного конденсатора тратится безвозвратно, преобразуясь в тепло. В результате затраты энергии постепенно уменьшается её запас и амплитуда контура уменьшается до нуля. Следовательно, колебания в контуре будут затухающими.(рис 4.2.7.3)
Для характеристики интенсивности затухания свободных колебаний введено понятие «затухание контура». Затуханием называется отношение активного сопротивления контура к его характеристическому сопротивлению.
Величина, обратная затуханию, называется добротностью контура.
Добротность характеризует качество контура.
Рассмотрим различные варианты последовательного соединения элементов в цепях переменного тока.
4.2.7. Гармонические колебания в цепи при параллельном соединении элементов R,L,C.
К цепи, содержащей параллельное соединение R,L,C
(рис. 4.2.8.1 а) приложено напряжение u= sin t. Согласно первому закону Кирхгофа (ЗТК) ток в неразветвленной части равен:
,
где, =G ,
,
.
Полная проводимость цепи будет равна:
Активная проводимость:
Реактивная проводимость:
При параллельном соединении элементов строят треугольники токов и проводимостей (рис.4.2.8.1.б,в)
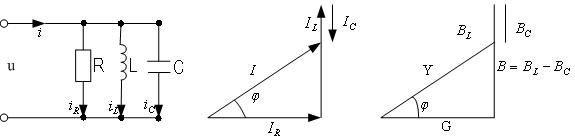
а) б) в)
Рис. 4.2.8.1.
4.2.8. Резонанс в электрических цепях переменного тока.
В радиотехнике и электросвязи большое значение имеет явление резонанса. Такое явление возникает в цепях, содержащих участки, с емкостным и индуктивным характером. Если цепь содержит последовательно соединенные с генератором элементы, то она называется последовательным колебательным контуром.(рис. 4.2.9.1а). Если элементы соединены параллельно с генератором, то цепь носит название – параллельный колебательный контур. (рис. 4.2.9.1б).
Среди многообразия частот имеется частота, на которой в цепи происходит обмен энергией между магнитными и электрическими полями. К генератору энергия не возвращается. От генератора поступает в контур столько энергии, сколько её тратится на активном сопротивлении цепи, тем самым обеспечиваются незатухающие колебания в контуре.
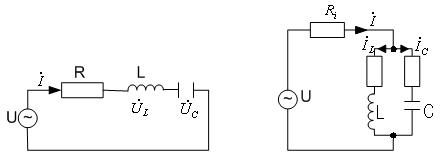
а) б)
рис. 4.2.9.1
· Частоту, на которой наблюдается явление резонанса, называют резонансной и определяют по формуле:
;
· Характеристическим сопротивлением контура называют реактивные сопротивления на резонансной частоте и определяют как:
[Ом]
· Резонансные свойства контура характеризуются добротностью контура, которая равна:
Добротность контура зависит от внутреннего сопротивления генератора .
В последовательном колебательном контуре, (рис.4.2.9.1а) чем больше , тем больше потери энергии внутри источника, тем меньше добротность, что приводит к ослаблению резонансных свойств контура.
В параллельном колебательном контуре, (рис. 4.2.9.1б) если будет мало, то через него будет проходить большая часть разрядного тока конденсатора, что приведет к большим потерям, уменьшит добротность и ухудшит резонансные свойства контура.
Различают два типа резонансов. В последовательном колебательном контуре возникает резонанс напряжений, а в параллельном – резонанс токов. Свойства цепей при резонансе рассматриваются в следующей таблице:
Важной характеристикой колебательного контура является полоса пропускания – это полоса частот, в пределах которой величина не меньше 0,707 от своего максимального значения. Полосу пропускания можно определить по формуле:
Где: ; ; ; – граничные частоты, на которых величина равна 0,707 от своего максимального значения.
Колебательные контуры и явление резонанса широко используются в радиотехнике и электросвязи. В радиоприемниках и усилителях они являются избирательными цепями, в автогенераторах, электрических фильтрах, в корректорах и других устройствах являются частотно-зависимыми элементами.
Пример:
Электрическая цепь состоит из последовательно соединенных резистора R=15 Ом, катушки индуктивности L=636 мкГн и конденсатора C=600 пФ.
Определить резонансную частоту , характеристическое сопротивление , добротностьQ, затухание d. Чему равны ток , расходуемая в цепи мощность , напряжения на индуктивности , и емкости , если контур включен на напряжение U=1,8 B? Какую избирательность обеспечивает данный контур при расстройке на ?
Рассчитать и построить зависимости:
для значений обобщенной расстройки . Показать на графике полосу пропускания контура.
Решение:
,
,
,
,
.
Рассчитаем и построим заданные зависимости:
1.
2.
Вопросы для самоконтроля:
1. Что называется колебательным контуром?
2. Какие колебания называются свободными, вынужденными?
3. Что называется «резонансом напряжений»?
4. Что называется «резонансом токов»?
5. Условия возникновения резонансов
6. Что характеризует добротность контура?
7. Как определяется резонансная частота?
4.3. Расчет цепей символическим методом
Символический метод основан на использовании комплексных чисел.
Комплексное число состоит из вещественной А’ и мнимой А» частей. А = А’ + jА».
Комплексное число можно представить вектором на комплексно-числовой плоскости. (рис. 4.3.1.) Проекция вектора на вещественную ось (ось абцисс) соответствует вещественной части комплексного числа А’, проекция вектора на мнимую ось (ось ординат) соответствует коэффициенту при мнимой единице А»,
j-мнимая единица представляет собой поворотный множитель, умножение на который означает поворот вектора на 90° против часовой стрелки.
Комплексным числам А=3+ j4 и В= 5-j2
Соответствуют векторы А и В, изображенные на рис. 4.3.1.
Модуль комплексного числа соответствует длине вектора, изображающего это комплексное число.
Модуль комплексного числа:
|А|= ;
Т.е. |А|= ; |В|=
Углы и , образованные векторами А и В, называются аргументами комплексного числа
= arctg
Для приведенных примеров
= arctg =53°10′
= arctg =-21°40′
Существует 3 формы записи количественного числа:
1. Алгебраическая А = А’ + jА»
2. Тригонометрическая А=|А|cos +j|А|sin ,
Так как А’=|А| cos
А»=|А| sin
3. Показательная А=|А|е =5е
В=|В|е =5,4е
Для перевода из показательной формы в алгебраическую пользуются тригонометрической формой записи комплексного числа.
Для перевода из алгебраической в показательную форму определяют модуль и аргумент.
Комплексные числа можно складывать, вычитать, умножать и делить.
Сложение и вычитание комплексных чисел производят в алгебраической форме, а умножение и деление удобнее и проще производить в показательной форме.
При умножении комплексных чисел в показательной форме модули этих чисел перемножаются, а аргументы складываются:
При делении комплексных чисел в показательной форме этих чисел делятся, а аргументы вычитаются
Если ток и напряжение изменяется по синусоидальному закону
То их можно изобразить векторами и записать комплексными числами
Комплекс полного сопротивления цепи:
Алгебраическая форма записи комплекса полного сопротивления
Любую цепь переменного тока можно рассчитывать по закону постоянного тока, если все величины представить в комплексной форме.
Комплекс полной мощности цепи определяется произведением комплекса напряжения и сопряженного комплекса тока I. У сопряженного комплекса знак перед мнимой единицей j меняется на противоположный
где Р- активная мощность
Q- реактивная мощность
Пример
Определить полное сопротивление цепи (рис.4.3.2) напряжение на зажимах, мощности (активную, реактивную, полную) если
Решение
1. Полное сопротивление цепи
2. Напряжения на зажимах цепи
3. Полная мощность цепи
где Р=15.99 = 16 Вт – активная мощность
Q= -0.015 Вт – реактивная мощность
Вопросы для самоконтроля.
1 . Какие формы записи комплексных чисел вы знаете?
2. Сложите два числа
3. Перемножить два числа
4. Выражаем токи через потенциалы, ЭДС и сопротивления.
,
5. Примем
6. Подставляем полученные выражения токов в уравнение 1.
7. Подставим числовые значения и решаем полученное уравнение.
8. Определяем токи в ветвях.
Действительные направления токов совпадают с выбранными.
Тема №3: Трехфазные цепи. [Электротехника Электронное пособие для студентов очной и заочной форм обучения всех технических специальностей]
Основными приемниками электрической энергии являются электрические двигатели, применяемые для приведения в движение рабочих машин. Наиболее простые из них трехфазные асинхронные двигатели. Для производства, распределения и передачи электрической энергии применяют трехфазные генераторы.
Система, состоящая из трех цепей, в которой действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе и создаваемые одним источником – называется трехфазной.
Система будет симметричной, если будут равны амплитуды фаз и углы сдвига фаз между каждой парой ЭДС.
На рисунке 4.14а, изображены временные диаграммы ЭДС , на рисунке 4.14б, векторная диаграмма, а на 4.14в, иллюстрируется принцип получения трехфазной системы ЭДС . В равномерном магнитном поле с постоянной угловой скоростью вращаются три одинаковых жёстко скрепленных друг с другом катушки.
Плоскости катушек смещены в пространстве относительно друг друга на 120°. В каждой катушке находится синусоидальная ЭДС одинаковой амплитуды. Уравнения ЭДС записывают в следующем виде:
а)
ЕА
ЕС ЕВ
б) в)
Рисунок 5.11
Векторы вращающиеся против часовой стрелки и фазы чередуются А, В, С, что называют прямой последовательностью фаз.
Источник
