Какая величина характеризует магнитные свойства среды
При проведении опыта с соленоидом, соединенным с баллистическим гальванометром, во время включения тока в нем можно определить значение магнитного потока Φ, который будет пропорционален отбросу стрелки гальванометра. Если делать его дважды с одинаково установленным током I в гальванометре, то в первом опыте соленоид будет без сердечника, а во втором его введут перед включением тока.
Проведение второго опыта дает понять, что наличие магнитного потока значительно больше, чем в первом. Если повторить процесс, но с задействованием сердечника разной толщины, то получаем максимальный поток при полном заполнении соленоида железом, то есть при плотно навитой обмотке на сердечнике. Имеем, что:
где Φ является магнитным потоком в катушке с сердечником, Φ0 – магнитным потоком без сердечника.
Увеличение магнитного потока при введении сердечника в соленоид обусловлено появлением магнитного потока, создаваемого совокупностью ориентированных амперовых молекулярных токов, и присоединение его к уже имеющемуся магнитному потоку от тока обмотки соленоида. Происходит ориентировка молекулярных токов под влиянием магнитного поля, их суммарный момент больше не равняется нулю, потому как происходит возникновение дополнительного магнитного поля.
Магнитная проницаемость. Измерения
Определение 1
Величина μ характеризует магнитные свойства среды и называется магнитной проницаемостью (относительной магнитной проницаемостью).
Она является безразмерной характеристикой вещества. Если происходит увеличение потока Φ в μ раз, это говорит о том, что магнитная индукция B→ в сердечнике во столько же раз больше, чем в вакууме при том же токе в соленоиде. Запись примет вид:
B→=μB0→, где B0→ означает магнитную индукцию поля в вакууме.
Вместе с магнитной индукцией, являющейся основной силовой характеристикой поля, применяют вспомогательную векторную величину – напряженность магнитного поля H→, которая связана с B→ при помощи соотношения:
B→=μH→.
Если формула B→=μH→ применится в опыте с сердечником, тогда при его отсутствии:
B0→=μ0H0→.
Значение μ=1. Если сердечник имеется, то
B→=μμ0H→.
Равенство B→=μB0→ выполняется, поэтому
μμ0H→=μм0H0→→H→=H0→.
Отсюда следует, что напряженность магнитного поля не зависит от характера однородного вещества, которым было заполнено пространство. Большинство веществ имеет магнитную проницаемость, равную 1. Исключениями считаются ферромагнетики.
Магнитная восприимчивость вещества
Обычно связь вектора намагниченности J→ и вектора напряженности в каждой точке магнетика обозначается:
J→=χH→.
Определение 2
χ является магнитной восприимчивостью. Величина безразмерная. Если вещество неферромагтиное и обладает небольшим полем, то χ не зависит от напряженности, является скалярной величиной.
Анизотропные среды предполагают χ в качестве тензора, направления J→ и H→ не совпадают.
Связь между магнитной восприимчивостью и магнитной проницаемостью
Из определения вектора напряженности магнитного поля:
H→=B→μ0-J→.
При подстановке выражения J→=χH→ в H→=B→μ0-J→ получаем:
H→=B→μ0-H→.
Напряженность приобретает вид:
H→=B→μ01+χ→B→=μ0(1+χ)H→.
При сравнении B→=μμ0H→ и H→=B→μ01+χ→B→=μ0(1+χ)H→:
μ=1+χ.
Магнитная восприимчивость может принимать как положительные, так и отрицательные значения. Из μ=1+χ имеем, что μ может быть больше или меньше 1.
Пример 1
Произвести вычисление намагниченности в центре кругового витка с радиусом R=0,1 м и током I=2 А при погружении в жидкий кислород. Значение магнитной восприимчивости жидкого кислорода χ=3,4·10-3.
Решение
Следует применить выражение, которое показывает связь напряженности магнитного поля и намагниченности, то есть:
J→=χH→.
Далее произведем поиск поля в центре витка с током, так как необходимо вычислить намагниченность в этой точке.
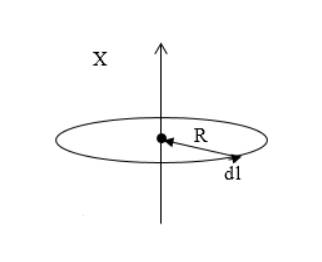
Рисунок 1
На проводнике с током необходимо выбрать элементарный участок, показанный на рисунке 1, как основу для решения задания. Применим формулу напряженности элемента витка с током.
Тогда:
dH=14πIdlsin υr2.
Где r→ – является радиус-вектором, проведенным из элемента тока в рассматриваемую точку,
dl→ – элемент проводника с током, υ – угол между dl→ и r→.
Опираясь на рисунок 1, υ=90°, следует упрощение J→=χH→. Так как расстояние от центра окружности элемента проводника с током постоянно и равняется радиусу витка R, получаем:
dH=14πIdlR2.
Направление результирующего вектора напряженности магнитного поля совпадает с осью Х. Его находят как сумму отдельных векторов dH→, потому что все элементы тока создают в центре витка магнитные поля, которые направлены вдоль нормали витка. Используя принцип суперпозиции, полная напряженность магнитного поля находится при переходе к интегралу вида:
H=∮dH.
Произведем подстановку dH=14πIdlR2 в H=∮dH:
H=14πIR2∮dl=14πIR22πR=12IR.
Для нахождения намагниченности, следует подставить значение напряженности из H=14πIR2∮dl=14πIR22πR=12IR в J→=χH→. тогда:
J=χ2IR.
Вычисляем с числовыми выражениями:
J=3,4·10-32·20,1=3,4·10-2 Ам.
Ответ: J=3,4·10-2 Ам.
Пример 2
Произвести вычисление доли суммарного магнитного поля в вольфрамовом стержне, находящегося во внешнем однородном магнитном поле, которую определяют молекулярные токи. Значение магнитной проницаемости вольфрама равняется μ=1,0176.
Решение
Нахождение индукции магнитного поля B’, приходящейся на долю молекулярных токов, представляется:
B’=μ0J, где J – является намагниченностью. Ее связь с напряженностью выражается через соотношение:
J=χH.
Магнитная восприимчивость находится из
χ=μ-1.
Магнитное поле молекулярных токов будет равно:
B’=μ0(μ-1)H.
По формуле находим полное поле в стержне:
B=μμ0H.
Задействовав выражения B’=μ0(μ-1)H, B=μμ0H, найдем соотношение:
B’B=μ0(μ-1)Hμμ0H=μ-1μ.
Подставим числовые выражения:
B’B=1,0176-11,0176=0,0173.
Ответ: B’B=0,0173.
Источник
Подобно тому, как в пространстве, окружающем электрические заряды, возникает электрическое поле, так и в пространстве окружающем токи, возникает особого вида поле, называемое магнитным полем.
Магнитное поле проявляется по силам, действующим на проводники с током, на движущиеся заряды или постоянные магниты.
Неподвижные электрические заряды не создают магнитное поле и постоянное магнитное поле не действует на неподвижные электрические заряды.
Опыт показывает, что неподвижный заряд и магнитная стрелка не влияют друг на друга.
При прохождении электрического тока по проводнику вокруг него возникает магнитное поле, действующее на магнитную стрелку, которая стремится занять положение поперек проводника при взгляде сверху.
Опыт Эрстеда (1820 г.), показывающий действие магнитного поля проводника с током на магнитную стрелку.
Характеристики магнитного поля
I. Вектор магнитной индукции (В) – совпадает по направлению с силой, действующей на северный полюс магнитной стрелки.
II. Линии магнитной индукции – кривые, в каждой точке которых, вектор магнитной индукции В направлен по касательной.
Свойства линий магнитной индукции
1. Линии магнитной индукции всегда замкнуты и охватывают проводники стоком.
2. Вблизи проводника линии магнитной индукции лежат в плоскости перпендикулярной проводнику с током.
3. Направление линий магнитной индукции определяется по правилу буравчика: если ввинчивать буравчик по направлению тока, то направление вращения его рукоятки укажет направление линий магнитной индукции.
Магнитное поле прямолинейного проводника с током.
Правило буравчика обратимо и для круговых токов его удобно применять в следующей формулировке: если вращать рукоятку буравчика по направлению кругового тока, то поступательное движение острия буравчика укажет направление линий магнитной индукции.
Линии магнитной индукции полей постоянного магнита, прямого тока, кругового тока и катушки с током.
Обратите внимание на аналогию магнитных полей постоянного магнита и катушки с током. Линии магнитной индукции всегда замкнуты, они нигде не обрываются. Это означает, что магнитное поле не имеет источников – магнитных зарядов. Силовые поля, обладающие этим свойством, называются вихревыми. Картину магнитной индукции можно наблюдать с помощью мелких железных опилок, которые в магнитном поле намагничиваются и, подобно маленьким магнитным стрелкам, ориентируются вдоль линий индукции.
III. Вектор напряженности магнитного поля H.
Согласно предположению французского физика А. Ампера, в любом теле существуют микроскопические (молекулярные) токи, обусловленные движением электронов в атомах и молекулах. Эти токи создают свое магнитное поле и могут поворачиваться в магнитных полях макроскопических токов (токов, текущих в проводниках). Так, если вблизи какого-то тела (среды) поместить проводник с током, то под действием его магнитного поля микротоки в атомах тела определенным образом ориентируются, создавая тем самым дополнительное магнитное поле. Поэтому вектор магнитной индукции B характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т.е. при одном и том же токе I и прочих равных условиях вектор B в различных средах будет иметь разные значения.
Магнитное поле, создаваемое макротоками, характеризуется вектором напряженности H. Для однородной изотропной среды связь между векторами индукции B и напряженности H магнитного поля определяется выражением
В =μ₀μН, где
магнитная постоянная, μ – магнитная проницаемость среды (безразмерная величина), показывающая, во сколько раз магнитное поле макротоков усиливается за счет поля микротоков данной среды.
Единица напряженности магнитного поля: 1 А/м – напряженность такого поля, магнитная индукция которого в вакууме равна 4π·10-7 Тл.
Источник
Магнитная проницаемость | |
Физическая величина, показывающая, во сколько раз индукция магнитного поля в одной среде больше или меньше индукции магнитного поля в вакууме, называется магнитной проницаемостью µ.. | |
Вещество, создающее собственное магнитное поле, называетсянамагниченным. Намагниченность возникает при помещении вещества во внешнее магнитное поле. Гипотеза Ампера: магнитные свойства тела определяются микроскопическими электрическими токами (орбитальное движение электронов в атомах, наличие у электрона собственного магнитного момента, имеющего квантовую природу) внутри вещества. Если направления этих токов неупорядочены, порождаемые ими магнитные поля компенсируют друг друга, т.е. тело не намагничено. Во внешнем магнитном поле происходит упорядочение этих токов, вследствие чего в веществе и возникает “собственное” магнитное поле (намагниченность). | |
Магнитные свойства вещества
| |
Для пара- и диамагнетиков намагниченность I прямо пропорциональна индукции B0 магнитного поля в вакууме. | |
3. Ферромагнетики— µ >>1. µстали = 8.103 (железо, никель, кобальт и их сплавы). Сплав железа с никелем: µ =2,5.105. Свойства ферромагнетиков
| |
Для характеристики явления намагничивания вещества вводится величина Iназываемая намагниченностью вещества. Намагниченность в СИ определяется формулой Для ферромагнитных тел намагниченность Iявляется сложной нелинейной функцией B0. Зависимость I от величины Во/µ0 называется кривой намагниченности (рис.2). Кривая указывает на явление магнитного насыщения: начиная с некоторого значения Во/µ0= В0н/µ0, намагниченность практически остается постоянной, равной Iн(намагниченность насыщения). | |
Магнитным гистерезисом (От греческого «hysteresis» — отставание следствия от его причины) ферромагнетика называется отставание изменения величины намагниченности ферромагнитного вещества от изменения внешнего магнитного поля, в котором находится вещество. Важнейшей причиной магнитного гистерезиса является характерная для ферромагнетика зависимость его магнитных характеристик (µ, I) не только от состояния вещества в данный момент, но и от значений величин µ и I в предыдущие моменты времени. Таким образом, существует зависимость магнитных свойств от предшествующей намагниченности вещества. Петлей гистерезиса называется кривая зависимости изменения величины намагниченности ферромагнитного тела, помещенного во внешнее магнитное поле, от изменения индукции этого поля от + Во/µ0 до – Во/µ0 и обратно. Значение + Во/µ0 соответствует намагниченности насыщения Iн. Для того чтобы полностью размагнитить ферромагнитное тело, необходимо изменить направление внешнего поля. При некотором значении магнитной индукции – В0к , которой соответствует величина В0к/µ0, называемая коэрцитивной(задерживающей) силoй, намагниченность I тела станет равной нулю. | |
Коэрцитивная сила и форма петли гистерезиса характеризуют свойство ферромагнетика сохранять остаточное намагничивание и определяют использование ферромагнетиков для различных целей. Ферромагнетики с широкой петлей гистерезиса называются жесткими магнитными материалами (углеродистые, вольфрамовые, хромовые, алюминиево-никелевые и другие стали). Они обладают большой коэрцитивной силой и используются для создания постоянных магнитов различной формы (полосовых,подковообразных, магнитных стрелок). К мягким магнитным материалам,обладающим малой коэрцитивной силой и узкой петлей гистерезиса, относятся железо, сплавы железа с никелем. Эти материалы используются для изготовления сердечников трансформаторов, генераторов и других устройств, по условиям работы которых происходит перемагничивание в переменных магнитных петлях. Перемагничивание ферромагнетика связано с поворотом областей самопроизвольного намагничивания. Работа, необходимая для этого, совершается за счет энергии внешнего магнитного поля. Количество теплоты, выделяющейся при перемагничивании, пропорционально площади петли гистерезиса. | |
При температурах меньших точки Кюри любое ферромагнитное тело состоит из доменов — малых областей с линейными размерами порядка 10-2 -10-3 см, внутри которых существует наибольшая величина намагниченности, равная намагниченности насыщения. Домены называются иначе областями самопроизвольной намагниченности. В отсутствие внешнего магнитного поля векторы магнитных моментов отдельных доменов ориентированы внутри ферромагнетика совершенно беспорядочно, так что суммарный магнитный момент всего тела равен нулю (рис.). Под влиянием внешнего магнитного поля в ферромагнетиках происходит поворот вдоль поля магнитных моментов не отдельных атомов или молекул, как в парамагнетиках, а целых областей самопроизвольной намагниченности – доменов. При увеличении внешнего поля размеры доменов, намагниченных вдоль внешнего поля, растут за счет уменьшения размеров доменов с другими (не совпадающими с направлением внешнего поля) ориентациями. При достаточно сильном внешнем магнитном поле все ферромагнитное тело оказывается намагниченным. Величина намагниченности достигает максимального значения – наступает магнитное насыщение. В отсутствие внешнего поля часть магнитных моментов доменов остается ориентированной, и этим объясняется существование остаточной намагниченности и возможность создания постоянных магнитов. Применение ферромагнетиков в технике. Роторы генераторов и электродвигателей; сердечники трансформаторов, электромагнитных реле; в электронно-вычислительных машинах (ЭВМ), телефонах, магнитофонах, на магнитных лентах. | |
Источник
Магни́тная проница́емость — безразмерная физическая величина, характеризующая изменение магнитной индукции В среды под воздействием магнитного поля и напряженностью Н.
Магнитная проницаемость различна для разных сред и зависит от ее свойств, поэтому принято говорить о магнитной проницаемости конкретной среды (имея вввиду ее состав, состояние, температуру и т. д.).
В случае однородной изотропной среды магнитная проницаемость μ:
μ = В/(μoН),
В анизотропных кристаллах магнитная проницаемость — тензор.
Большинство веществ по значению магнитной проницаемости делятся на три класа:
- диамагнетики (μ < 1),
- парамагнетики (μ > 1)
- ферромагнетики (обладающие более выраженными магнитными свойствами, например железо).
Магнитная проницаемость сверхпроводников равна нулю.
Абсолютная магнитная проницаемость воздуха приблизительно равна магнитной проницаемости вакуума и в технических расчетах принимается равной 4π · 10-7 Гн/м
μ = 1 + χ (в единицах СИ);
μ = 1 + 4πχ (в единицах СГС).
Магнитная проницаемость физического вакуума μ =1, так как χ=0.
Магнитная проницаемость показывает, во сколько раз абсолютная магнитная проницаемость данного материала больше магнитной постоянной, т.е., во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды. Магнитная проницаемость воздуха и большинства веществ, за исключением ферромагнитных материалов, близка к единице.
В технике используется несколько видов магнитной проницаемости в зависимости от конкретных применений магнитного материала. Относительная магнитная проницаемость показывает, во сколько раз в данной среде сила взаимодействия между проводами с током изменяется по сравнению с вакуумом. Численно равна отношению абсолютной магнитной проницаемости к магнитной постоянной. Абсолютная магнитная проницаемость равна произведению магнитной проницаемости на магнитную постоянную.
У диамагнетиков χμχ>0 и μ > 1. В зависимости от того, измеряется ли μ ферромагнетиков в статическом или переменном магнитном поле, ее называют соответственно статической или динамической магнитной проницаемостью.
Магнитная проницаемость ферромагнетиков сложным образом зависит от Н. Из кривой намагничивания ферромагнетика можно построить зависимость магнитной проницаемости от Н.
Магнитную проницаемость, определенную по формуле:
μ = В/(μoН),
называют статической магнитной проницаемостью.
Она пропорциональна тангенсу угла наклона секущей, проведенной из начала координат через соответствующую точку на основной кривой намагничивания. Предельное значение магнитной проницаемости μн при напряженности магнитного поля, стремящейся к нулю, называют начальной магнитной проницаемостью. Эта характеристика имеет важнейшее значение при техническом использовании многих магнитных материалов. Экспериментально ее определяют в слабых магнитных полях с напряженностью порядка 0, 1 А/м.
При одновременном воздействии на магнитный материал постоянного Нo и переменного Н~ магнитных полей и, обычно, при условии Н~o вводят понятие дифференциальной проницаемости μдиф .
Крутизну отдельных участков кривой намагничивания и ветвей петли гистерезиса также характеризуют дифференциальной магнитной проницаемостью:
μдиф =(1/μо)*(dB/dH)/
В одном и том же образце максимальное значение дифференциальной проницаемости всегда превышает максимальное значение статической проницаемости.
Источник
