Какая векторная величина обладает свойством сохранения
Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Как отличить скалярную величину от векторной?
Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.
Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.
При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.
Какие действия чаще всего выполняются с векторами?
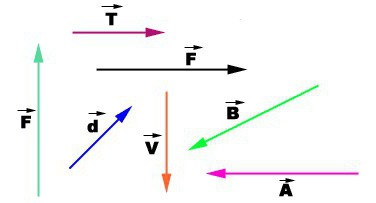
Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.
Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.
Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Какие векторы изучают в физике?
Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.
| Обозначение в формуле | Наименование |
| v | скорость |
| r | перемещение |
| а | ускорение |
| F | сила |
| р | импульс |
| Е | напряженность электрического поля |
| В | магнитная индукция |
| М | момент силы |
Теперь немного подробнее о некоторых из этих величин.
Первая величина — скорость
С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.
Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.
Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.
Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.
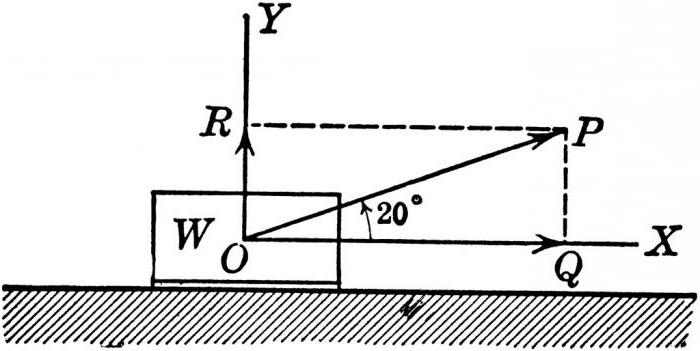
Вторая величина — сила
Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.
| Сила | Точка приложения | Направление |
| тяжести | центр тела | к центру Земли |
| всемирного тяготения | центр тела | к центру другого тела |
| упругости | место соприкосновения взаимодействующих тел | против внешнего воздействия |
| трения | между соприкасающимися поверхностями | в сторону, противоположную движению |
Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.
Третья величина — перемещение
Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.
Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Четвертая величина — ускорение
Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.
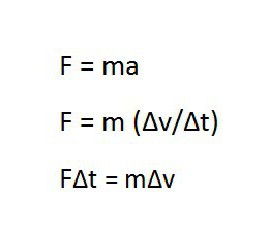
Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.
В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.
Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.
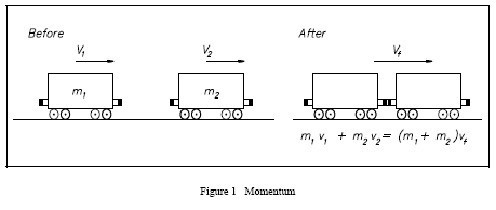
Задача о неупругом ударе
Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона – 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы “вагон-платформа” после удара.
Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2. По условию задачи необходимо узнать значение скорости v.
Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.
В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.
Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.
Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.
Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.
Ответ. Скорость вагона с платформой равна 0,75 м/с.
Задача с разделением тела на части
Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?
Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2.
Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.
В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.
Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м/с.
Ответ. Скорость маленького осколка равна 25 м/с.
Задача про выстрел под углом
Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.
Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.
За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.
Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.
Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = – Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.
Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.

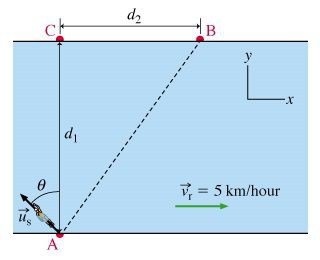
Задача о переправе через реку
Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.
Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2).
2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
v = √(v22 – v12), тогда t = l / (√(v22 – v12)).
Ответ. 1). s = l * (v1 / v2), 2). sin α = v1 / v2, t = l / (√(v22 – v12)).
Источник
Тест к разделу «Механика»
Оценка: «5» – 90% выполнения, «4» – 80%; «3» -60%
Тест №1 Тема. Кинематика
1. Перемещение – это:
1)векторная величина; 2) скалярная величина; 3) может быть и векторной и скалярной величиной; 4) правильного ответа нет.
2.Модуль перемещения при криволинейном движении в одном направлении:
1) равен пройденному пути; 2) больше пройденного пути; 3) меньше пройденного пути; 4) правильного ответа нет.
3. При прямолинейном движении скорость материальной точки направлена:
1) туда же, куда направлено перемещение; 2) против направления перемещения; 4) независимо от направления перемещения;
4. При криволинейном движении мгновенная скорость материальной точки в каждой точке траектории направлена:
1) по траектории; 2) по касательной к траектории в этой точке; 3) по радиусу кривизны траектории.
5. Перемещением движущейся точки называют…
1) …длину траектории; 2) пройденное расстояние от начальной точки траектории до конечной; 3)… направленный отрезок прямой, соединяющий начальное положение точки с его конечным; 4) …линию, которую описывает точка в заданной системе отсчета.
6. Средняя скорость характеризует:
1) равномерное движение; 2) неравномерное движение;
7. Физическая величина, равная отношению перемещения материальной точки к физически малому промежутку времени, в течение которого произошло это перемещение, называется
1) средней скоростью неравномерного движения материальной точки; 2) мгновенной скоростью материальной точки; 3) скоростью равномерного движения материальной точки.
8. Направление ускорения всегда совпадает с:
1) направлением скорости; 2) направлением перемещения; 3) направлением вектора изменения скорости.
9. Ускорение – это:
1) физическая величина, равная отношению изменения скорости к тому промежутку времени, за который это изменение произошло; 2) физическая величина, равная отношению изменения скорости к тому физически малому промежутку времени, за которое это изменение произошло; 3) физическая величина, равная отношению перемещения ко времени.
10. Проекция ускорения на координатную ось может быть:
1) только положительной; 2) только отрицательной; 3) и положительной, и отрицательной, и равной нулю.
11. В каком случае модуль ускорения больше?
1) тело движется с большой постоянной скоростью; 2) тело быстро набирает или теряет скорость; 3) тело медленно набирает или теряет скорость.
12.Два поезда движутся навстречу друг другу по прямолинейному участку пути. Один из них движется ускоренно, второй замедленно. Их ускорения направлены:
1) в одну сторону; 2) в противоположные стороны; 3) однозначно об их направлениях нельзя сказать.
13. Локомотив разгоняется до скорости 20м/с, двигаясь по прямой с ускорением 5м/с2. Начальная скорость его равна нулю. Сколько времени длится разгон?
1) 0,25с; 2) 2с; 3) 100 с; 4) 4с.
14. При подходе к станции поезд уменьшил скорость на 10м/с в течение 20с. С каким ускорением двигался поезд?
1) – 0,5м/с2 ; 2) 2м/с2 ; 3) 0,5 м/с2; 4) – 2м/с2.
15. Автомобиль, трогаясь с места, движется с ускорением 3м/с2. Через 4с скорость автомобиля будет равна:
1)12 м/с; 2) 0,75 м/с; 3) 48 м/с ; 4) 6 м/с.
Кинематика
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
3
1
2
3
2
2
3
2
3
2
1
4
1
1
Тест №2
Тема: Законы Ньютона
16.Какие из величин (скорость, сила, ускорение, перемещение) при механическом движении всегда совпадают по направлению?
1)сила и ускорение; 2) сила и скорость; 3) сила и перемещение; 4) ускорение и перемещение.
17.Какие силы в механике сохраняют свое значение при переходе из одной инерциальной системы в другую?
1) силы тяготения, трения, упругости; 2) только сила тяготения; 3) только сила упругости; 4) только сила трения.
18. Равнодействующая сила – это:
1) сила, действие которой заменяет действие всех сил, действующих на тело; 2) сила, заменяющая действие сил, с которыми взаимодействуют тела.
19. Равнодействующая всех сил, действующих на тело, равна нулю. Какова траектория движения этого тела?
1) парабола; 2) окружность; 3) прямая; 4) эллипс.
20. В инерциальной системе отсчета F сообщает телу массой m ускорение a. Как изменится ускорение тела, если массу тела и действующую на него силу уменьшить в 2 раза?
1) увеличится в 4 раза; 2) уменьшится в 4 раза; 3) уменьшится в 8 раз; 4) не изменится.
21. После открытия парашюта парашютист под действием силы тяжести и силы сопротивления воздуха двигался вниз с ускорением, направленным вверх. Как станет двигаться парашютист, когда при достижении некоторого значения скорости равнодействующая силы тяжести и силы сопротивления воздуха окажется равной нулю?
1) равномерно и прямолинейно вверх; 2) равномерно и прямолинейно вниз; 3) с ускорением свободного падения вниз; 4) будет неподвижным.
22. Закон инерции открыл
1) Демокрит; 2) Аристотель; 3) Галилей; 4) Ньютон.
23. Третий закон Ньютона описывает:
1) действие одного тела на другое; 2) действие одной материальной точки на другую; 3) взаимодействие двух материальных точек.
24. Локомотив сцеплен с вагоном. Сила, с которой локомотив действует на вагон, равна силам, препятствующим движению вагона. Другие силы на движение вагона не влияют. Систему отсчета, связную с Землей, считайте инерциальной. В этом случае:
1) вагон может только покоится; 2) вагон может только двигаться с постоянной скоростью; 3) вагон движется с постоянной скоростью или покоится; 4) вагон движется с ускорением.
25. Яблоко массой 0,3 кг падает с дерева. Выберите верное утверждение
1) яблоко действует на Землю силой 3Н, а Земля не действует на яблоко; 2) Земля действует на яблоко с силой 3Н, а яблоко не действует на Землю; 3) яблоко и Земля не действуют друг на друга; 4) яблоко и Земля действуют друг на друга с силой 3 Н.
26. При действии силы в 8Н тело движется с ускорением 4м/с2. Чему равна его масса?
1) 32 кг; 2) 0,5кг; 3) 2 кг; 4) 20кг.
27.Сила тяги ракетного двигателя первой отечественной экспериментальной ракеты на жидком топливе равнялась 660Н. Стартовая масса ракеты была равна 30кг. Какое ускорение приобретала ракета во время старта?
1) 22м/с2; 2) 45м/с2; 3) 0,1м/с2; 4) 19800 м/с2.
28. Скорость лыжника при равноускоренном спуске с горы за 4с увеличилась на 6м/с. Масса лыжника 60кг. Равнодействующая всех сил, действующих на лыжника, равна
1) 20 Н; 2) 30 Н; 3) 60 Н; 4) 90 Н.
29. Материальная точка массой 1кг движется под действием двух взаимно перпендикулярных сил 8Н и 6Н. Ускорение точки равно
1) 2м/с2; 2) 3,7 м/с2; 3) 10м/с2; 4) 14 м/с2.
30. Какая из физических характеристик не меняется при переходе от одной инерциальной системы отсчета к другой?
1) ускорение; 2) перемещение; 3) траектория; 4) кинетическая энергия.
Законы Ньютона
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
1
1
3
4
2
3
3
3
4
3
1
4
3
1
Тест №3
Тема. Силы в природе
31.Закон всемирного тяготения позволяет рассчитать силу взаимодействия двух тел, если
1)тела являются телами Солнечной системы; 2) массы тел одинаковы; 3) известны массы тел и расстояние между их центрами; 4) известны массы тел и расстояние между ними, которое много больше размеров тел.
32.Согласно закону Гука сила натяжения пружины при растягивании прямо пропорциональна
1) ее длине в свободном состоянии; 2) ее длине в натянутом состоянии; 3) разнице между длиной в натянутом и свободном состояниях; 4) сумме длин в натянутом и свободном состояниях.
33. Спортсмен совершает прыжок с шестом. Сила тяжести действует на спортсмена
1)только в течение того времени, когда он соприкасается с поверхностью Земли; 2) только в течение того времени, когда он сгибает шест в начале прыжка; 3) только в течение того времени, когда он падает вниз после преодоления планки; 4) во всех этих случаях.
34. Вес тела:
1) свойство тела; 2) физическая величина; 3) физическое явление.
35.Сила тяготения – это сила обусловленная:
1) гравитационным взаимодействием; 2) электромагнитным взаимодействием; 3) и гравитационным, и электромагнитным взаимодействием.
36. Вдоль границ соприкосновения тел направлены силы:
1) вязкого трения; 2) сухого трения; 3) и сухого, и вязкого трения.
37. При сухом трении максимальная сила трения покоя:
1) больше силы трения скольжения; 2) меньше силы трения скольжения; 3) равна силе трения скольжения.
38. Сила упругости направлена:
1) против смещения частиц при деформации; 2) по направлению смещения частиц при деформации; 3) о ее направлении нельзя ничего сказать.
39.Как изменяются масса и вес тела при его перемещении с экватора на полюс Земли?
1) масса и вес тела не изменяются; 2) масса тела не изменяется, вес увеличивается; 3) масса тела не изменяется, вес уменьшается; 4) масса и вес тела уменьшаются.
40. Космический корабль после выключения ракетных двигателей движется вертикально вверх, достигает верхней точки траектории и затем движется вниз. На каком участке траектории в корабле наблюдается состояние невесомости? Сопротивление воздуха пренебрежимо мало.
1) только во время движения вверх; 2) только во время движения вниз; 3) только в момент достижения верхней точки траектории; 4) во время всего полета с неработающими двигателями.
41. Космонавт на Земле притягивается к ней с силой 700Н. С какой приблизительно силой он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса в 2 раза, а а масса – в 10 раз меньше, чем у Земли?
1) 70Н; 2) 140 Н; 3) 210 Н; 4) 280Н.
42. Под действием силы 3Н пружина удлинилась на 4 см, а под действием силы 6Н удлинилась на 8см. Чему равен модуль силы, под действием которой удлинение пружины составило 6 см?
1) 3,5Н; 2) 4Н; 3) 4,5 Н; 4) 5Н.
43. При скольжении бруска массой 5кг по горизонтальной поверхности сила трения равна 10Н. Чему равен коэффициент трения скольжения для этой пары тел?
1) 0,5; 2) 0,2; 3) 2; 4) 5.
44. Автомобиль массой 1000кг едет по выпуклому мосту с радиусом кривизны 40м. какую скорость должен иметь автомобиль в верхней точке моста, чтобы пассажиры в этой точке почувствовали состояние невесомости?
1) 0,05м/с; 2) 20м/с; 3) 25 м/с; 4) 400м/с.
45. Расстояние между центрами двух шаров равно 1м, масса каждого шара 1 кг. Сила всемирного тяготения между ними примерно равна
1) 1Н; 2) 0,001Н; 3) 7·10-5Н; 4) 7·10-11Н.
Силы в природе
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
4
3
4
2
1
3
1
1
2
4
4
3
2
2
4
Тест №4
Тема. Законы сохранения в механике
46.Импульс системы, состоящей из нескольких материальных точек, равен:
сумме модулей импульсов всех ее материальных точек; 2) векторной сумме импульсов всех ее материальных точек; 3) импульсы нельзя складывать.
47.Утверждение о том, что импульсы замкнутой системы тел не изменяются, является:
1) необоснованным; 2) физическим законом; 3) вымыслом; 4) затрудняюсь что-либо сказать по этому поводу.
48. Мальчик массой 50кг, стоя на очень гладком льду, бросает груз массой 8кг под углом 600 к горизонту со скоростью 5м/с. Какую скорость приобретет мальчик?
1)5,8м/с; 2) 1,36 м/с; 3) 0,8м/с; 4) 0,4 м/с.
49. Товарный вагон, движущийся по горизонтальному пути с небольшой скоростью, сталкивается с другим вагоном и останавливается. При этом пружина буфера сжимается. Какое из перечисленных ниже преобразований энергии наряду с другими происходит в этом процессе?
1) кинетическая энергия вагона преобразуется в потенциальную энергию пружины; 2) кинетическая энергия вагона преобразуется в его потенциальную энергию; 3) потенциальная энергия пружины преобразуется в ее кинетическую энергию; 4) внутренняя энергия пружины преобразуется в кинетическую энергию вагона.
50. Кинетическая энергия тела 8 Дж, а величина импульса 4 Н·с, Масса тела равна…
1)0,5кг; 2) 1 кг; 3) 2 кг; 4) 32 кг.
51. Навстречу друг другу летят шарики из пластилина. Модули их импульсов равны соответственно 0,03кгм/с и 0,04 кгм/с. Столкнувшись, шарики слипаются. Импульс слипшихся шариков равен
1).01кг·м/с; 2). 00351кг·м/с; 3).0,05кг·м/с; 4) 0,07кг·м/с;
52. Тело движется по прямой. Под действием постоянной силы величиной 4 Н за 2 с импульс тела увеличился и стал равен 20кг·м/с. Первоначальный импульс тела равен
1) 4кг·м/с; 2) 8кг·м/с; 3) 12кг·м/с; 4) 28кг·м/с;
53. Какую работу надо совершить, чтобы лежащий на земле однородный стержень длиной 2м и массой 100кг поставить вертикально, медленно поднимая один его конец?
1) 100Дж; 2) 200 Дж; 3) 1000 Дж; 4) 2000 Дж.
54. Величина работы может быть отрицательной?
1)может; 2) не может; 3) об этом ничего нельзя сказать.
55. Процесс работы – это:
1) любой процесс превращения энергии; 2) процесс превращения энергии, не связанный с движением тел; 3) процесс превращения энергии при действии сил на движущееся тело.
56.Кинетическая энергия:
1) может быть отрицательной величиной; 2) не может быть отрицательной величиной; 3) может быть и отрицательной, и положительной.
57. Кинетической энергией тело обладает благодаря:
1) взаимодействию с другими телами; 2) благодаря своему движению; 3)благодаря своей деформации.
58. Платформа массой 10т движется со скоростью 2 м/с. Ее нагоняет платформа массой 15т, движущаяся со скоростью 3 м/с. Какой будет скорость этих платформ после автосцепки?
1) 2,6 м/с; 2) 13 м/с; 3) 26м/с; 4) 5м/с.
59. Спортсмен поднял штангу массой 75 кг на высоту 2м. Потенциальная энергия штанги при этом изменилась на
1) 37,5 Дж; 2) 150 Дж; 3) 300 Дж; 4) 1500 Дж.
60. Тело массой 2 кг брошено вертикально вверх с поверхности земли со скоростью 10м/с. На какой высоте потенциальная и кинетическая энергия тела совпадают?
1)1 м; 2) 2 м; 3) 2,5 м; 4) 5 м.
Законы сохранения в механике
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
2
2
4
1
2
1
3
2
1
3
2
2
1
4
3
Источник
