Какая информация содержится в видеопамяти

§20. Как кодируется изображение
Основные темы параграфа:
– кодирование цветов пикселей;
– объем видеопамяти.
Изучаемые вопросы:
– Принцип формирования цвета пикселя на экране.
– Связь между количеством цветов в палитре и количеством бит для кодирования одного пикселя (формула).
– Формула определения объёма видеопамяти для хранения изображения заданного размера.
Кодирование цветов пикселей
Информация о состоянии каждого пикселя хранится в закодированном виде в памяти компьютера. Код может быть однобитовым, двухбитовым и т. д.
 Код пикселя — это информация о цвете пикселя.
Код пикселя — это информация о цвете пикселя.
Для получения черно-белого изображения (без полутонов) используются два состояния пикселя: светится — не светится (белый — черный). Тогда для кодирования цвета пикселя достаточно одного бита памяти:
1 — белый;
0 — черный.
Количество цветов, в которые может быть окрашен пиксель на цветном дисплее, больше двух. Поэтому одного бита на пиксель недостаточно.
Для кодирования четырехцветного изображения требуется двухбитовый код, поскольку с помощью двух битов можно выразить четыре различных значения (отобразить четыре различных состояния). Может использоваться, например, такой вариант кодирования цветов:
00 — черный;
10 — зеленый;
01 — красный;
11 — коричневый.
Из трех базовых цветов — красного, зеленого, синего — можно получить восемь комбинаций трехбитового кода:
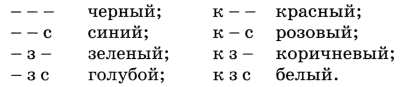
В этом коде каждый базовый цвет обозначается его первой буквой (к — красный, з — зеленый, с — синий). Черточка означает отсутствие цвета.
Следовательно, для кодирования восьмицветного изображения требуются три бита памяти на один видеопиксель. Если наличие базового цвета обозначить единицей, а отсутствие — нулем, то получается таблица кодировки восьмицветной палитры (табл. 4.1).
Таблица 4.1. Двоичный код восьмицветной палитры
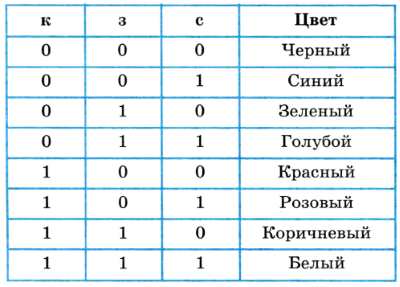
Из сказанного, казалось бы, следует вывод: с помощью трех базовых цветов нельзя получить палитру, содержащую больше восьми цветов. Однако на экранах современных компьютеров получают цветные изображения, составленные из сотен, тысяч и даже миллионов различных оттенков. Как это достигается?
Если иметь возможность управлять интенсивностью (яркостью) свечения базовых цветов, то количество различных вариантов их сочетаний, дающих разные оттенки, увеличивается.
Шестнадцатицветная палитра получается при использовании четырехразрядной кодировки пикселя: к трем битам базовых цветов добавляется один бит интенсивности. Этот бит управляет яркостью всех трех цветов одновременно (интенсивностью трех электронных пучков) (табл. 4.2).
Таблица 4.2. Двоичный код шестнадцатицветной палитры.
«и» — бит интенсивности
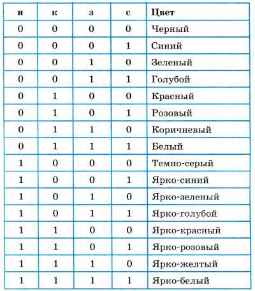
Большее количество цветов получается при раздельном управлении интенсивностью базовых цветов. Причем интенсивность может иметь более двух уровней, если для кодирования интенсивности каждого из базовых цветов выделять больше одного бита.
Из сказанного можно вывести правило.
 Количество различных цветов К и количество битов для их кодирования b связаны между собой формулой К = 2b.
Количество различных цветов К и количество битов для их кодирования b связаны между собой формулой К = 2b.
21 = 2, 22 = 4, 23 = 8, 24 = 16 и т. д. Для получения цветовой гаммы из 256 цветов требуется 8 битов = 1 байт на каждый пиксель, так как 28 = 256.
 Величина b называется битовой глубиной цвета.
Величина b называется битовой глубиной цвета.
Объем видеопамяти
Объем необходимой видеопамяти определяется размером графической сетки дисплея и количеством цветов. Минимальный объем видеопамяти должен быть таким, чтобы в него помещался один кадр (одна страница) изображения. Например, для сетки 640 х 480 и черно-белого изображения минимальный объем видеопамяти должен быть таким:
640 • 480 • 1 бит = 307 200 битов = 38 400 байтов.
Это составляет 37,5 Кбайт.
Для работы с 256-цветной палитрой на мониторе с разрешением 1024 х 768 минимальный объем видеопамяти составляет 768 Кб.
На современных высококачественных дисплеях используется палитра более чем из 16 миллионов цветов (b = 24 бита). Требуемый объем видеопамяти в этом случае — несколько мегабайтов.
На самом деле видеопамять хранит одновременно не одно изображение экрана, а множество. Это способствует быстрой смене кадров. Поэтому размер видеопамяти на современных ПК составляет от сотен мегабайтов до нескольких гигабайтов.
Коротко о главном
Информация в видеопамяти — это двоичные коды, обозначающие цвета пикселей на экране.
Для кодирования двух цветов достаточно 1 бита на пиксель; четырех цветов — 2 битов; восьми цветов — 3 битов; шестнадцати цветов — 4 битов и т. д. Количество цветов К и размер кода в битах (битовая глубина цвета) b связаны формулой К = 2b.
Из трех базовых цветов можно получить 8 различных цветов. Большее число цветов получается путем управления интенсивностью базовых цветов.
Минимально необходимый объем видеопамяти зависит от размера сетки пикселей и от количества цветов. Обычно в видеопамяти помещается несколько страниц (кадров) изображения одновременно.
Вопросы и задания
1. Какая информация содержится в видеопамяти?
2. Сколько битов видеопамяти на один пиксель требуется для хранения двухцветного; четырехцветного; восьмицветного; шестнадцатицветного изображения?
3. Какие цвета получаются из смешения красного и синего, красного и зеленого, зеленого и синего цветов?
4. Сколько цветов будет содержать палитра, если каждый базовый цвет кодировать двумя битами?
5. Придумайте способ кодирования цветов для 256-цветной палитры.
6. Пусть видеопамять компьютера имеет объем 512 Кбайт. Размер графической сетки — 640 х 480. Сколько страниц экрана одновременно разместится в видеопамяти при палитре из 16 цветов; 256 цветов?
Электронное приложение к уроку


Cкачать материалы урока
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 13 июля 2020; проверки требуют 2 правки.
Видеопамять — это внутренняя оперативная память, отведённая для хранения данных, которые используются для формирования изображения на экране монитора.
При этом в видеопамяти может содержаться как непосредственно растровый образ изображения (экранный кадр), так и отдельные фрагменты как в растровой (текстуры), так и в векторной (многоугольники, в частности треугольники) формах.
Как правило, чипы оперативной памяти современной видеокарты припаяны прямо к текстолиту печатной платы, в отличие от съёмных модулей системной памяти, которые вставляются в стандартизированные разъёмы ранних видеоадаптеров.
При изготовлении видеокарт уже достаточно давно используется память GDDR3. На смену ей пришла GDDR4, которая имеет более высокую пропускную способность, чем GDDR3; однако GDDR4 не получила широкого распространения вследствие плохого соотношения «Цена-производительность» и ограниченно использовалась лишь в некоторых видеокартах верхнего ценового сегмента (например Radeon X1950XTX, HD 2900 XT, HD3870). Далее появилась память GDDR5, которая по состоянию на 2012 год является наиболее массовой, GDDR3 используется в бюджетном сегменте. В 2018 году в топовых видеокартах устанавливается память типа HBM и HBM2, GDDR5X и GDDR6.
Также видеопамять отличается от «обычной» системной ОЗУ более жёсткими требованиями к ширине шины.
Графическая шина данных — это магистраль, связывающая графический процессор и память видеокарт.
Шина данных видеопамяти бывает:
- 32-битной.
- 64-битной.
- 128-битной.
- 192-битной. (нестандартная шина памяти)
- 256-битной.
- 320-битной. (нестандартная шина памяти)
- 384-битной. (нестандартная шина памяти)
- 448-битной. (нестандартная шина памяти)
- 512-битной.
- 768-битной. (нестандартная шина памяти)
- 896-битной. (нестандартная шина памяти)
- 1024-битной.
- 2048-битной (только HBM-память)
- 3072-битной (только HBM2-память)
- 4096-битной (только HBM2-память)
Имеет значение соотношение количества памяти, её типа и ширины шины данных: 512 МБ DDR2, при ширине шины данных в 128 бит, будет работать медленнее и гораздо менее эффективно, чем 256 МБ GDDR3 при ширине шины в 128 бит и т. п. По понятным причинам, 256 МБ GDDR3 с шириной шины 256 бит лучше, чем 256 МБ GDDR3 с шириной шины в 128 бит и т. п.
Также стоит учитывать, что из-за относительно невысокой стоимости видеопамяти многие производители видеокарт устанавливают избыточное количество видеопамяти (4, 6 и 8 Гбайт) на слабые видеокарты с целью повышения их маркетинговой привлекательности.
Требования операционных систем и компьютерных игр возрастают с течением времени; так, например, чтобы играть комфортно в наиболее современные игры на высоких настройках[источник не указан 1395 дней]:
- на период 2008—2009 года требовалось порядка 512 МБ (и более) GDDR3 256 бит или 2 ГБ (и более) DDR2(3),
- на период 2010 года требовалось порядка 768 МБ (и более) GDDR4 320 бит или 3 ГБ (и более) DDR3,
- на период 2011 года требовалось порядка 1024 МБ (и более) GDDR5 256 бит или 3-4 ГБ (и более) DDR3.
- на период 2014 года требовалось порядка 3072 МБ (и более) GDDR5 256 бит
- на период 2015 года требовалось порядка 4096 МБ (и более) GDDR5 256 бит
- на период 2017 года требовалось порядка 6144 МБ (и более) GDDR5 256 бит
- на период 2018 года требуется порядка 8192 МБ (и более) GDDR5 256 бит
- на период 2020 года требуется порядка 8192 МБ (и более) GDDR6 256 бит
См. также[править | править код]
- Видеокарта
- Графический процессор
- Видеоконтроллер
Примечания[править | править код]
Ссылки[править | править код]
- Алексей Берилло, Руководство покупателя видеокарты: выбор объёма видеопамяти // iXBT.com, 28 сентября 2012 года
Источник
Палитра (N) – количество используемых в наборе цветов .
Глубина цвета (I) – количество бит (двоичных разрядов), отводимых в видеопамяти под каждый пиксель.
Каждый цвет имеет свой уникальный двоичный код.
Код цвета пикселя содержит информацию о доле каждого базового цвета.
Число цветов, воспроизводимых на экране монитора (N), и число бит, отводимых под кодирование цвета одного пикселя (I), находится по формуле: N=2I
Глубина цвета и количество отображаемых цветов
| Глубина цвета (I) | Количество отображаемых цветов (N) |
| 8 | 28=256 |
| 16 (High Color) | 216=65 536 |
| 24 (True Color) | 224=16 777 216 |
| 32 (True Color) | 232=4 294 967 296 |
V=K*I,
где V – информационный объем рисунка (файла), К – общее количество точек рисунка или разрешающая способность монитора, I – глубина цвета.
1. Растровый файл, содержащий черно-белый рисунок, имеет объем 300 байт. Какой размер может иметь рисунок в пикселях?
Решение: Объем файла V = 300 б = 2400 бит. Рисунок черно-белый, значит, палитра состоит из двух цветов (черный, белый), т.е. N=2. Отсюда находим глубину цвета I= 1 бит.
К=V/I=2400 бит/1 бит=2400 пикселей.
Ответ: Рисунок может состоять из 2400 пикселей.
2. Сколько информации содержится в картинке экрана с разрешающей способностью 800х600 пикселей и 16 цветами?
Решение:
Количество точек К=800х600=480000
Глубина цвета I=4 бита, т.к. 24=16
480000·4 бит = 1920000 бит = 240000 б= 234,375 Мб ≈ 0,23 Кб
3. Определить объем видеопамяти компьютера, который необходим для реализации графического режима монитора High Color с разрешающей способностью 1024х768 точек и палитрой из 65536 цветов.
Решение: Глубина цвета составляет: I=log265536=16 бит.
216=65535
Количество точек изображения равно:
1024х768=786 432.
Требуемый объем видеопамяти равен:
16 бит·768 432= 12 582 912 бит ≈1,2 Мбайта
4. Достаточно ли видеопамяти объемом 256 Кб для работы монитора в режиме 640х480 и палитрой из 16 цветов?
Решение: Палитра N = 16, следовательно, глубина цвета I = 4 бита (24=16).
Общее количество точек равно: 640 · 480 = 307200.
Информационный объем равен:
307200 · 4 бита = 1228800 бит = 153600 байт = 150 Кб
Ответ: видеопамяти достаточно, 150 Кб < 256 Кб
5. Определить максимально возможную разрешающую способность экрана монитора с диагональю 15″ и размером точки экрана 0,28 мм.
Решение: Выразим размер диагонали в сантиметрах (1 дюйм = 2,54 см):
2,54 см · 15 = 38,1 см
Определим соотношение между высотой и шириной экрана для режима 1024х768 точек:
768 : 1024 = 0,75
Определим ширину экрана. Пусть ширина экрана равна L, тогда высота равна 0,75L.
По теореме Пифагора имеем:
L2 + (0,75L)2 = 38,12
1,5625L2 = 1451,61
L2 ≈ 929
L ≈ 30,5 см
Количество точек по ширине экрана равно:
305 мм : 0,28 мм = 1089
Максимально возможным разрешением экрана монитора является 1024х768.
6. Сканируется цветное изображение размером 10х10 см. Разрешающая способность сканера 600 dpi и глубина цвета 32 бита. Какой информационный объем будет иметь полученный графический файл?
Решение: Разрешающая способность сканера 600 dpi (dot per inch – точек на дюйм) означает, что на отрезке длиной 1 дюйм сканер способен различить 600 точек.
Переведем разрешающую способность сканера из точек на дюйм (1 дюйм = 2,54 см) в точки на сантиметр:
600dpi : 2,54 ≈ 236 точек/см.
Следовательно, размер изображения в точках составит
2360х2360 точек.
Общее количество точек изображения равно:
2360 · 2360 = 5 569 600.
Информационный объем файла равен:
32 бита · 5569600 = 178 227 200 бит = 22278400 б = 21756 Кб ≈ 21 Мб
7. Какую часть экрана займет изображение файла типа ВМР объемом 3 Мбайт, созданного при глубине цвета, равной 32 бита, при разрешении экрана 1024х768 точек и качестве цветопередачи 32 бита?
1) Весь экран. 2) ½ экрана. 3) 1/3 экрана. 4) ¼ экрана.
Решение:
1) (1024 х 768 х 32)/8 – информационный объем изображения рабочего стола, выраженный в байтах.
2)3х210х210/(210х768х25)/23 = 210/(256х22) = 210/210 = 1.
8. Фотография размером 10х10 была отсканирована с разрешением 400 dpi при глубине цвета, равной 24 бита. Определите информационную емкость полученного растрового файла.
1) 7,3 Мб. 2) 940 Кб. 3) 150 Кб. 4) 7,3 Кб.
Решение:
1) 10/0,25 = 4 (дюйм)
2) 4 х 400 = 1600 (пиксел).
(1600 х 1600 х24)/8 = (24 х 100 х 24 х 100 х 3) = 28 х 3 х 104 = 7 680 000 (байт) = 7,3 Мб.
Задачи для самостоятельной работы
1. Чему равен информационный объем одной точки черно-белого растрового изображения?
2. Чему равен информационный объем одной точки 16-цветного растрового изображения?
3. Чему равен информационный объем одной точки 256-цветного растрового изображения?
4. 256-цветное изображение файла типа ВМР имеет размер 1024 х 768 пикселей. Определите информационную емкость файла.
5. Какой объем памяти видеокарты займет изображение 32-разрядного файла типа ВМР, экранный размер которого 1024 х 768 пикселей?
6. После изменения свойств рабочего стола монитор приобрел разрешение 1024 х 768 точек и получил возможность отображать 65 536 цветов. Какой объем видеопамяти занимает текущее изображение рабочего стола?
7. Для хранения растрового изображения размером 128 x 128 пикселей отвели 4 КБ памяти. Каково максимально возможное число цветов в палитре изображения.
8. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея – 800 х 600 пикселей?
9. В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Во сколько раз уменьшится объем занимаемой им памяти?
10. Укажите минимальный объем памяти (в килобайтах), достаточный для хранения любого растрового изображения размером 256 х 256 пикселей, если известно, что в изображении используется палитра из 216 цветов. Саму палитру хранить не нужно.
Источник
Теория
Расчёт информационного объёма растрового графического изображения (количества информации, содержащейся в графическом изображении) основан на подсчёте количества пикселей в этом изображении и на определении глубины цвета (информационного веса одного пикселя).
При расчетах используется формула V = i * k,
где V – это информационный объём растрового графического изображения, измеряющийся в байтах, килобайтах, мегабайтах;
k – количество пикселей (точек) в изображении, определяющееся разрешающей способностью носителя информации (экрана монитора, сканера, принтера);
i – глубина цвета, которая измеряется в битах на один пиксель.
Глубина цвета задаётся количеством битов, используемым для кодирования цвета точки.
Глубина цвета связана с количеством отображаемых цветов формулой
N = 2i, где N – это количество цветов в палитре, i – глубина цвета в битах на один пиксель.
Примеры
1. Видеопамять компьютера имеет объем 512Кб, размер графической сетки 640×200, в палитре 8 цветов. Какое количество страниц экрана может одновременно разместиться в видеопамяти компьютера?
Решение:
Найдем количество пикселей в изображении одной страницы экрана:
k = 640*200=128000 пикселей.
Найдем i (глубину цвета, т.е. сколько бит потребуется для кодировки одного цвета) N = 2i, следовательно, 8 = 2i, i = 3.
Находим объем видеопамяти, необходимый для размещения одной станицы экрана. V = i * k (бит), V = 3*128000 = 384000(бит) = 48000 (байт) = 46,875Кб.
Т.к. объем видеопамяти компьютера 512Кб, то можно одновременно хранить в видеопамяти компьютера 512 / 46,875 = 10,923 ≈ 10 целых страниц экрана.
Ответ: 10 полных страниц экрана можно одновременно хранить в видеопамяти компьютера
2. В результате преобразования растрового графического изображения количество цветов уменьшилось с 256 до 16. Как при этом изменился объем видеопамяти, занимаемой изображением?
Решение:
Используем формулы V = i * k и N = 2i.
N1 = 2i1, N2 = 2i2, затем V1 = i1 * k, V2 = i2 * k, следовательно,
256 = 2i1, 16 = 2i2,
i1 = 8, i2 = 4,
V1 = 8 * k, V2 = 4 * k.
V2 / V1 = 1/2
Ответ: объём графического изображения уменьшится в два раза.
3. Сканируется цветное изображение стандартного размера А4 (21×29,7 см2). Разрешающая способность сканера 1200dpi (точек на один дюйм) и глубина цвета 24 бита. Какой информационный объём будет иметь полученный графический файл?
Решение:
1дюйм=2,54 см
i=24 бита на пиксель;
Переведем размеры изображения в дюймы и найдем количество пикселей k: k = (21/2,54)*(29,7/2,54)*12002(dpi) ≈ 139210118 (пикселей)
Используем формулу V = i * k
V=139210118*24 = 3341042842 (бита) = 417630355байт = 407842Кб = 398Мб
Ответ: объём сканированного графического изображения равен 398 Мб
Задачи для самостоятельного решения
1. Определите количество цветов в палитре при глубине цвета 4, 8, 16, 24, 32 бита.
2. В процессе преобразования растрового графического изображения количество цветов уменьшилось с 65536 до 16. Во сколько раз уменьшится информационный объем файла?
3. 256-цветный рисунок содержит 120 байт информации. Из скольких точек он состоит?
4. Достаточно ли видеопамяти объёмом 256 Кбайт для работы монитора в режиме 640×480 и палитрой из 16 цветов?
5. Какой объем видеопамяти необходим для хранения двух страниц изображения при условии, что разрешающая способность дисплея равна 640×350 пикселей, а количество используемых цветов – 16?
6. Какой объем видеопамяти необходим для хранения четырех страниц изображения, если битовая глубина равна 24, а разрешающая способность дисплея 800×600 пикселей?
7. Объем видеопамяти равен 2 Мб, битовая глубина 24, разрешающая способность дисплея 640×480. Какое максимальное количество страниц можно использовать при этих условиях?
8. Видеопамять имеет объем, в котором может храниться 4-х цветное изображение размером 640×480. Какого размера изображение можно хранить в том же объеме видеопамяти, если использовать 256 – цветную палитру?
9. Для хранения растрового изображения размером 1024×512 отвели 256 Кб памяти. Каково максимальное возможное количество цветов в палитре изображения?
Задачи на расчет объёма звуковой информации
Теория
Звук может иметь различные уровни громкости. Количество различных уровней рассчитывается по формуле N = 2i, где i – глубина звука.
Частота дискретизации – количество измерений уровня входного сигнала в единицу времени (за 1 секунду).
Размер цифрового моноаудиофайла вычисляется по формуле А=Д*Т*i,
где Д- частота дискретизации;
Т- время звучания или записи звука;
i – разрядность регистра (глубина звука).
Для стереоаудиофайла размер вычисляется по формуле А=2*Д*Т*i
Примеры
1. Подсчитать, сколько места будет занимать одна минута цифрового звука на жестком диске или любом другом цифровом носителе, записанного с частотой 44.1 кГц и разрядностью 16 бит.
Решение:
Если записывают стереосигнал
А = 2*Д*Т*i = 44100*120*16 = 84672000бит = = 10584000байт = 10335,9375Кб = 10,094Мб.
Если записывают моносигнал А = 5Мб.
Ответ: 10 Мб, 5Мб
2. Объем свободной памяти на диске – 0,01 Гб, разрядность звуковой платы – 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц.
Решение:
А = Д * Т * i
Т =А / Д / i
Т = 10737418,24/44100/2 = 121,74(сек) = 2,03(мин)
Ответ: 2,03 мин.
Задачи для самостоятельного решения
1. Определить размер (в байтах) цифрового аудиофайла, время звучания которого составляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен.
2. В распоряжении пользователя имеется память объемом 2,6 Мб. Необходимо записать цифровой аудиофайл с длительностью звучания 1 минута. Какой должна быть частота дискретизации и разрядность?
3. Объем свободной памяти на диске – 0,01 Гб, разрядность звуковой платы – 16. Какова длительность звучания цифрового аудиофайла, записанного с частотой дискретизации 44100 Гц?
4. Одна минута записи цифрового аудиофайла занимает на диске 1,3 Мб, разрядность звуковой платы – 8. С какой частотой записан звук?
Источник
