Какая функция называется обратной пропорциональностью свойства
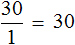
Представим, что у нас есть тело, движущееся равномерно от города А к городу В. Время, которое наше тело затрачивает на прохождение указанного пути зависит от скорости движения. Предположим, что расстояние между А и В равно 120 м, v – это скорость движения (м/с), а t – это время движения (с). Тогда получим, что
t = 120/v.
Подставим вместо v несколько значений и получим t:
если v = 5, то t = 120/5 = 24; если v = 10, то t = 120/10 = 12;
если v = 20, то t = 120/20 = 6.
Получается, что каждому значению переменной v (v > 0) соответствует единственное значение t. Формулой t = 120/v, где v > 0, задается функция.
Обратной пропорциональностью называется функция, которую можно задать формулой вида у = k/х, где k – не равное нулю число.
Относительно переменной у говорится, что она обратно пропорциональна переменной х.
Т.к. выражение k/х при любом значении х, кроме 0, имеет смысл, то областью определения функции, задаваемой формулой у = k/х, может служить множество всех чисел, отличных от нуля, или какое-нибудь его подмножество.
Из формулы у = k/х следует, что ху = k. Верно и обратное: если ху = k (k ≠ 0), то у = k/х. Логично, что, чтобы выяснить, является ли обратной пропорциональностью функция х – у, необходимо сравнить произведения ху для всех соответственных значений х и у. Если эти произведения равны одному и тому же числу k, где k ≠ 0, то функция f является обратной пропорциональностью.
Определим, является ли обратной пропорциональностью функция m – n, заданная значениями:
если m = 1, то n = 15;
если m = 2, то n = 7,5;
если m = 3, то n = 5;
если m = 5, то n = 3;
если m = 6, то n = 2,5;
если m = 10, то n = 1,5;
если m = 15, то n = 1.
Для каждой пары (m; n) соответственных значений m и n найдем произведение mn:
если m = 1, n = 15, то mn = 15;
если m = 2, n = 7,5, то mn = 15;
если m = 3, n = 5, то mn = 15;
если m = 5, n = 3, то mn = 15;
если m = 6, n = 2,5, то mn = 15;
если m = 10, n = 1,5, то mn = 15;
если m = 15, n = 1, то mn = 15.
В результате получаем, что найденные произведения равны одному и тому же числу 15. Следовательно, функция f – обратная пропорциональность.
Решим задачу.
Пусть а – основание прямоугольника (см), b – его высота (см). Если площадь прямоугольника остается постоянной, то с изменением длины его основания должна изменяться и его высота. Является ли зависимость переменной b от переменной а обратной пропорциональностью?
Для любой пары соответственных значений переменных а и b произведение аb равно одному и тому же числу, выражающему площадь прямоугольника в см2. Следовательно, зависимость b от а – обратная пропорциональность.
Вернемся к примеру с равномерным движением тела из города А в город В. Возьмем два произвольных значения переменной v: v1 = 5 и v2 = 6. Тогда соответствующие им значения переменной t: t1 = 24 и t2 = 20.
Найдем частное v1/v2и частное t1/t2:
v1/v2 = 5/6; t1/t2 = 6/5.
Отметим, что частное v1/v2 равно числу, обратному частному t1/t2. К такому же выводу мы придем, если выберем иные значения переменных.
Т.о., если функция х → у – обратная пропорциональность и (х1; у1), (х2; у2) – пары соответственных значений переменных х и у, то х1/х2 = у2/у1.
Докажем это. Из формулы у = k/х имеем, что у1 = k/х1, у2 = k/х2, причем у1 ≠ 0, у2 ≠ 0. Отсюда
у2/у1 = (k/х2) / (k/х1) = (k/х2) ∙ ( х1/ k) = х1/х2.
Если значения переменных х и у – это положительные числа, то рассмотренное свойство обратной пропорциональности можно определить так:
с увеличением значения х в несколько раз соответствующее значение у уменьшается во столько же раз; аналогично: с уменьшением значения х в несколько раз соответствующее значение у увеличивается во столько же раз.
Применим установленное свойство к решению задач.
Задача.
Велосипедист, двигаясь со скоростью 10 км/ч, проехал расстояние от города А до города В за 6 ч. Сколько времени затратит велосипедист на обратный путь, если будет двигаться со скоростью 12 км/ч?
за 6 ч. Сколько времени затратит велосипедист на обратный путь, если будет двигаться со скоростью 12 км/ч?
Решение.
Пусть на обратный путь велосипедист затратит х ч. Т.к. время, необходимое для прохождения одного и того же расстояния, обратно пропорционально скорости движения, то х/6 = 10/12. Отсюда 12х = 60, х = 5.
Ответ: велосипедисту понадобится 5 ч.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Источник
Графиком обратной пропорциональности является гипербола, расположенная в I и III четверти, если k>0; во II и IV четверти, если k<0.
Свойства обратной пропорциональности:
1) Область определения функции – множество всех действительных чисел, кроме нуля:
D(y)=(−; 0)(0; +).
Е(y)=(−; 0)(0; +).
3) , Функция является нечётной, её график симметричен относительно начала координат, т.е. точки (0;0).
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.
Для точного построения графика, например, функции , возьмём несколько значений х и для каждого вычислим значение у.
Так как график функции симметричен относительно начала координат, то точки в III четверти будут иметь противоположные координаты.
II. Обратная пропорциональность где k ≠ 0.
Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Ох на т единиц вправо, если т > 0, и влево, если т < 0. Чтобы построить график этой функции, проводим дополнительную прямую х = т, параллельную оси Оу, затем строим график функции относительно получившихся осей.
Свойства:
1) Область определения функции – множество всех действительных чисел, кроме х = т:
D(y)=(−; т)(т; +).
2) Область значений функции – множество всех действительных чисел, кроме нуля:
Е(y)=(−; 0)(0; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.
III. Обратная пропорциональность где k ≠ 0.
Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Оу на п единиц вверх, если п > 0, и вниз, если п < 0. Чтобы построить график этой функции, проводим дополнительную прямую у = п, параллельную оси Ох, затем строим график функции относительно получившихся осей.
Свойства:
1) Область определения функции – множество всех действительных чисел, кроме нуля:
D(y)=(−; 0)(0; +).
2) Область значений функции – множество всех действительных чисел, кроме у = п:
Е(y)=(−; п)(п; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.
IV. Обратная пропорциональность где k ≠ 0.
Графиком данной функции является гипербола, которая получается из графика функции смещением вдоль оси Ох на т единиц вправо, если т > 0, и влево, если т < 0, и вдоль оси Оу на п единиц вверх, если п > 0, и вниз, если п < 0. Чтобы построить график этой функции, проводим дополнительные прямые х = т, параллельную оси Оу , и у = п, параллельную оси Ох, затем строим график функции относительно получившихся осей.
Свойства:
1) Область определения функции – множество всех действительных чисел, кроме х = т:
D(y)=(−; т)(т; +).
2) Область значений функции – множество всех действительных чисел, кроме у = п:
Е(y)=(−; п)(п; +).
3) , значит, функция не является ни чётной, ни нечётной, её график не симметричен относительно оси Оу. и не симметричен относительно начала координат.
4) При k > 0 функция убывает, а при k < 0 возрастает на всей области определения.
Источник
Сегодня мы рассмотрим, какие величины называются обратно пропорциональными, как выглядит график обратной пропорциональности и как все это может вам пригодится не только на уроках математики, но и вне школьных стен.
Такие разные пропорциональности
Пропорциональностью называют две величины, которые взаимно зависимы друг от друга.
Зависимость может быть прямой и обратной. Следовательно, отношения между величинами описывают прямая и обратная пропорциональность.
Прямая пропорциональность – это такая зависимость двух величин, при которой увеличение либо уменьшение одной из них ведет к увеличению либо уменьшению другой. Т.е. их отношение не изменяется.
Например, чем больше усилий вы прилагаете для подготовки к экзаменам, тем выше ваши оценки. Или чем больше вещей вы берете с собой в поход, тем тяжелее нести ваш рюкзак. Т.е. количество затраченных на подготовку к экзаменам усилий прямо пропорционально полученным оценкам. И количество запакованных в рюкзак вещей прямо пропорционально его весу.
Обратная пропорциональность – это функциональная зависимость, при которой уменьшение либо увеличение в несколько раз независимой величины (ее называют аргументом) вызывает пропорциональное (т.е. во столько же раз) увеличение либо уменьшение зависимой величины (ее называют функцией).
Проиллюстрируем простым примером. Вы хотите купить на рынке яблок. Яблоки на прилавке и количество денег в вашем кошельке находятся в обратной пропорциональности. Т.е. чем больше вы купите яблок, тем меньше денег у вас останется.
Функция и ее график
Функцию обратной пропорциональности можно описать как y = k/x. В котором x ≠ 0 и k ≠ 0.
Эта функция обладает следующими свойствами:
- Областью ее определения является множество всех действительных чисел, кроме x = 0. D(y): (-∞; 0) U (0; +∞).
- Областью значений являются все действительные числа, кроме y = 0. Е(у): (-∞; 0) U (0; +∞).
- Не имеет наибольших и наименьших значений.
- Является нечетной и ее график симметричен относительно начала координат.
- Непериодическая.
- Ее график не пересекает оси координат.
- Не имеет нулей.
- Если k > 0 (т.е. аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (т.е. аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
- При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные – (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные – (-∞; 0).
График функции обратной пропорциональности называется гиперболой. Изображается следующим образом:
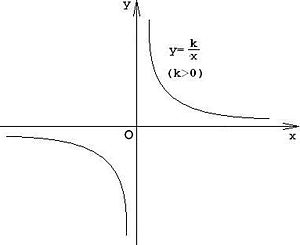
Задачи на обратную пропорциональность
Чтобы стало понятнее, давайте разберем несколько задач. Они не слишком сложные, а их решение поможет вам наглядно представить, что такое обратная пропорциональность и как эти знания могут пригодиться в вашей обычной жизни.
Задача №1. Автомобиль движется со скоростью 60 км/ч. Чтобы доехать до места назначения, ему потребовалось 6 часов. Сколько времени ему потребуется, чтобы преодолеть такое же расстояние, если он будет двигаться со скоростью в 2 раза выше?
Можем начать с того, что запишем формулу, которая описывает отношения времени, расстояния и скорости: t = S/V. Согласитесь, она очень напоминает нам функцию обратной пропорциональности. И свидетельствует о том, что время, которое автомобиль проводит в пути, и скорость, с которой он движется, находятся в обратной пропорциональности.
Чтобы убедиться в этом, давайте найдем V2, которая по условию выше в 2 раза: V2 = 60 * 2 = 120 км/ч. Затем рассчитаем расстояние по формуле S = V * t = 60 * 6 = 360 км. Теперь совсем несложно узнать время t2, которое требуется от нас по условию задачи: t2 = 360/120 = 3 ч.
Как видите время в пути и скорость движения действительно обратно пропорциональны: со скоростью в 2 раза выше изначальной автомобиль потратит в 2 раза меньше времени на дорогу.
Решение этой задачи можно записать и в виде пропорции. Для чего сначала составим такую схему:
↓ 60 км/ч – 6 ч ↑
↓120 км/ч – х ч ↑
Стрелки обозначают обратно пропорциональную зависимость. А также подсказывают, что при составлении пропорции правую часть записи надо перевернуть: 60/120 = х/6. Откуда получаем х = 60 * 6/120 = 3 ч.
Задача №2. В мастерской трудятся 6 рабочих, которые с заданным объемом работы справляются за 4 часа. Если количество рабочих сократить в 2 раза, сколько времени потребуется оставшимся, чтобы выполнить тот же объем работы?
Запишем условия задачи в виде наглядной схемы:
↓ 6 рабочих – 4 ч ↑
↓ 3 рабочих – х ч ↑
Запишем это в виде пропорции: 6/3 = х/4. И получим х = 6 * 4/3 = 8 ч. Если рабочих станет в 2 раза меньше, оставшиеся затратят на выполнение всей работы в 2 раза больше времени.
Задача №3. В бассейн ведут две трубы. Через одну трубу вода поступает со скоростью 2 л/с и наполняет бассейн за 45 минут. Через другую трубу бассейн наполнится за 75 минут. С какой скоростью вода поступает в бассейн через эту трубу?
Для начала приведем все данные нам по условию задачи величины к одинаковым единицам измерения. Для этого выразим скорость наполнения бассейна в литрах в минуту: 2 л/с = 2 * 60 = 120 л/мин.
Поскольку из условия следует, что через вторую трубу бассейн заполняется медленнее, значит, и скорость поступления воды ниже. На лицо обратная пропорциональность. Неизвестную нам скорость выразим через х и составим такую схему:
↓ 120 л/мин – 45 мин ↑
↓ х л/мин – 75 мин ↑
А затем составим пропорцию: 120/х = 75/45, откуда х = 120 * 45/75 = 72 л/мин.
В задаче скорость наполнения бассейна выражена в литрах в секунду, приведем полученный нами ответ к такому же виду: 72/60 = 1,2 л/с.
Задача №4. В небольшой частной типографии печатают визитки. Сотрудник типографии работает со скоростью 42 визитки в час и трудится полный рабочий день – 8 часов. Если бы он работал быстрее и печатал 48 визиток за час, насколько раньше он смог бы уйти домой?
Идем проверенным путем и составляем по условию задачи схему, обозначив искомую величину как х:
↓ 42 визитки/ч – 8 ч ↑
↓ 48 визитки/ч – х ч ↑
Перед нами обратно пропорциональная зависимость: во сколько раз больше визиток в час напечатает сотрудник типографии, во столько же раз меньше времени ему потребуется на выполнение одной и той же работы. Зная это, составим пропорцию:
42/48 = х/8, х = 42 * 8/48 = 7ч.
Таким образом, справившись с работой за 7 часов, сотрудник типографии смогу бы уйти домой на час раньше.
Заключение
Нам кажется, что эти задачи на обратную пропорциональность действительно несложные. Надеемся, что теперь вы тоже считаете их такими. А главное, что знание об обратно пропорциональной зависимости величин действительно может оказаться для вас полезным еще не раз.
Не только на уроках математики и экзаменах. Но и тогда, когда вы соберетесь отправиться в путешествие, пойдете за покупками, решите немного подработать в каникулы и т.п.
Расскажите нам в комментариях, какие примеры обратной и прямой пропорциональной зависимости вы замечаете вокруг себя. Пускай это будет такая игра. Вот увидите, как это увлекательно. Не забудьте «расшарить» эту статью в социальных сетях, чтобы ваши друзья и одноклассники тоже смогли поиграть.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Источник
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.
Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.
Прямая пропорциональность
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.
Изобразим на рисунке расстояние, пройденное автомобилем за 1 час
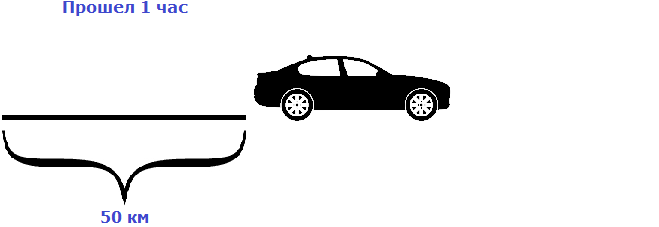
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км
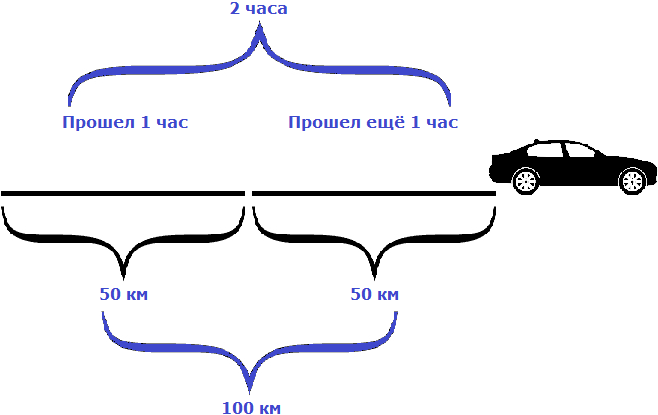
Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.
Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.
Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.
Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.
Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.
В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.
Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50
Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:
Это отношение можно прочитать следующим образом:
Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.
Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.
Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.
Запишем чему равно отношение тридцати рублей к одному килограмму
Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:
Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.
Обратная пропорциональность
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.
Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:
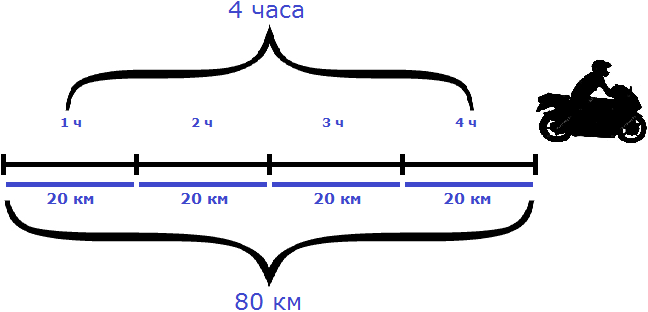
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.
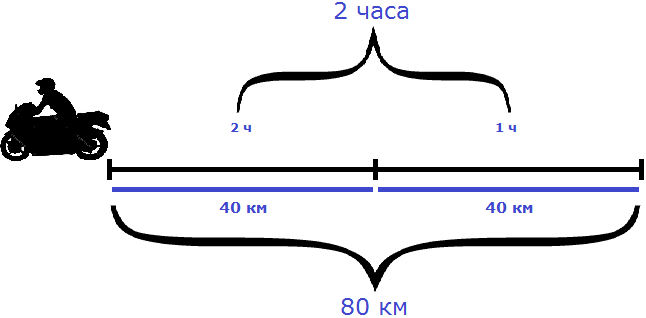
Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.
Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.
Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.
и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:
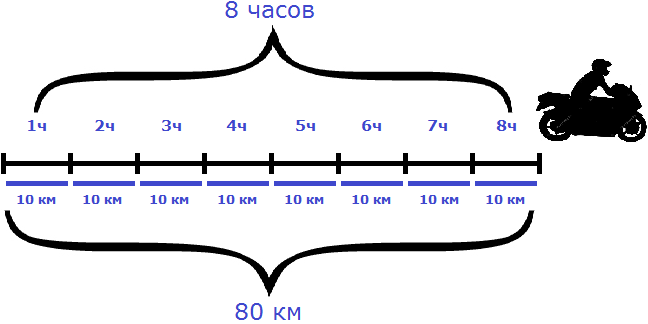
Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.
Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным
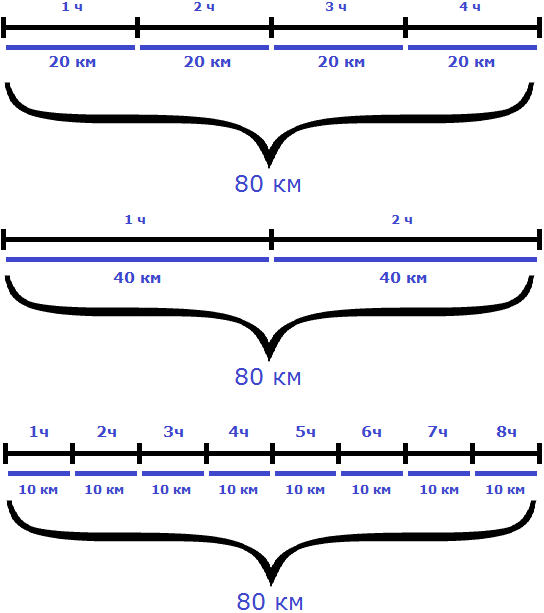
Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Источник
