Граф с какими свойствами называют деревом что такое ветви дерева

- 1
- 2
- 3
- 4
- 5
5.0/5, Голосов: 1
Задание 1. Что такое система; структура?
Система – объект, который состоит из взаимосвязанных элементов и существующий как единое целое.
Структура – определенный порядок объединения элементов, составляющих систему.
Задание 2. Назовите элементы, составляющие следующие системы: автомобиль, молекула воды, компьютер, магазин, Солнечная система, семья, футбольная команда, армия. Обоснуйте взаимозависимость элементов этих систем.
Автомобиль – двигатель, трансмиссия, рулевое управление, тормозная система, несущая система, подвеска и колёса.
Молекула воды – два атома водорода и один атом кислорода.
Компьютер – монитор, клавиатура, мышь, колонки и системный блок(материнская плата, жесткая и оперативная памяти, дисковод, блок питания, видеокарта и др.).
Магазин – касса, товар, полки, склад.
Солнечная система – планеты, карликовые планеты, спутники, малые тела и кометы.
Семья – родители и дети.
Футбольная команда – тренер, вратарь, защитник, полузащитник, нападающий, капитан, стартовый состав и запасные игроки.
Армия – солдаты, командир, оружие.
Задание 3. Что такое граф? Какую информацию он может нести в себе?
Граф – это совокупность объектов, связанные между собой линиями (связями), соединяющие вершины.
Задание 4. Как на графе изображаются элементы системы и отношения между ними?
Элементы системы – это вершины графа, которые изображаются овалами.
Отношения между элементами изображаются линиями, где направленная линия (со стрелкой) называется дугой, а если стрелки нет, то это ребро.
Задание 5. Что значит «симметричное отношение», «несимметричное отношение»? Как они изображаются на графе? Приведите примеры.
Симметричное отношение обозначает двустороннюю связь между элементами системы, которое изображается ненаправленной линией (ребром).
Примеры: муж и жена
Нессиметричное отношение обозначает одностороннюю связь между элементами системы, которое изображается направленной линией (дугой).
Примеры: Отец и сын, Неразделённая любовь
Задание 6. Дайте имена возможным связям между следующими объектами и изобразите связи между ними в форме графа: брат и сестра; ученик и школа; Саша и Маша; Москва и Париж; министр, директор, рабочий; Пушкин и Дантес; компьютер и процессор.
Симметричное отношение: брат – сестра; Саша – Маша; Москва – Париж.
Нессиметричное отношение: ученик директор –> рабочий; Пушкин процессор.
Задание 7. Граф с какими свойствами называют деревом? Что такое корень дерева, ветви, листья?
Дерево – это граф в котором нет петель, то есть связанных по замкнутой линии вершин. В направлении сверху вниз выполняется принцип «один ко многим».
Корень дерева – вершина нашего графа, в которую не ведут другие ребра.
Ветви – ребра дерева.
Листья – вершины, от которых не выходят ребра, то есть не имеют своих ветвей.
Задание 8. Какие системы называют иерархическими?
Иерархическая система называется системой, информационная модель которой представляется в виде дерева.
Задание 9. Можно ли систему файлов в Microsoft Windows (и подобных ей ОС) назвать иерархической? Какой смысл имеют связи между элементами этой системы? Что в ней является листьями, ветвями, корнем?
Да, можно. В этой системе файлов создаётся корневой каталог, в котором хранятся не только файлы, но и другие каталоги более низкого уровня (подкаталоги).
Листьями этого дерева являются файлы или подкаталоги, у которых нет своих ветвей. Корнем дерева является корневой каталог операционной системы. Ветвями являются стрелочки, по которым можно добраться до любого листа.
Задание 10. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения) — дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша.
Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?
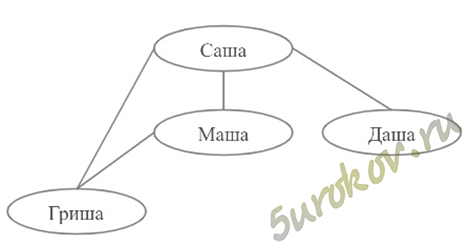
По графу можно понять, что Саша может поделиться секретом, не рискуя, только с Дашей, так как у нее нет никаких взаимоотношений между его друзьями Машей или Гришей. Маша и Гриша дружат и есть риск, что секрет кто-то из них расскажет.
Источник
Дерево – это частный случай графа, наиболее широко применяемый в программировании.
Основные определения
Существует довольно много равносильных определений деревьев, вот лишь некоторые из них.
Дерево – это связный граф без циклов.
Дерево – это связный граф, в котором при N вершинах всегда ровно N-1 ребро.
Дерево – это граф, между любыми двумя вершинами которого существует ровно один путь.
Аналогичным образом определяется и ориентированное дерево – как орграф, в котором между любыми двумя вершинами существует не более одного пути.
Деревом называют конечный связный граф с выделенной вершиной (корнем), не имеющей циклов.
Для каждой пары вершин дерева – узлов – существует единственный маршрут, поэтому вершины удобно классифицировать по степени удаленности от корневой вершины.
Расстояние до корневой вершины V0 называется ярусом s вершины.
Поскольку маршрут между двумя вершинами единственный, то , применяя это свойство к смежным вершинам, можно заключить, что любая ветвь является мостом.
При удалении ребра единственный маршрут прерывается и граф распадается на два подграфа.
Корневое дерево – это ориентированное дерево, в котором можно выделить вершины трех видов: корень, листья (другое их название: терминальные вершины) и остальные вершины (нетерминальные); причем должны выполняться два обязательных условия:
из листьев не выходит ни одна дуга; из других вершин может выходить сколько угодно дуг;
в корень не заходит ни одна дуга; во все остальные вершины заходит ровно по одной дуге.
Традиционно в математике и в родственных ей науках (в том числе и в теоретическом программировании) деревья “растут” вниз головой: это делается просто для удобства наращивания листьев в случае необходимости. Таким образом, на рисунках корень дерева оказывается самой верхней вершиной, а листья – самыми нижними.
Предок вершины v – это вершина, из которой исходит дуга, заходящая в вершину v. Потомок вершины v – это вершина, в которую заходит дуга, исходящая из вершины v. В этих терминах можно дать другие определения понятиям корень и лист: у корня нет предков, у листа нет потомков.
Бинарное дерево – это корневое дерево, каждая вершина которого имеет не более двух потомков. В таком случае иногда говорят о левом потомке и правом потомке для текущей вершины.
Высота корневого дерева – это максимальное количество дуг, отделяющих листья от корня. Если дерево не взвешенное, то его высота – это просто расстояние от корня до самого удаленного листа.
Свойства деревьев.
Граф G(V,X) является деревом тогда и только тогда, когда выполняется хотя бы одно из условий:
1. Чтобы простой связный граф был деревом, необходимо и достаточно, чтобы число вершин было больше числа ребер на один.
2. Чтобы граф был деревом, необходимо и достаточно, чтобы любые две вершины его соединялись единственным маршрутом.
3. Граф будет деревом тогда и только тогда, когда добавление любого нового ребра приводит к появлению ровно одного цикла.
4. Граф G(V,X) связен и не содержит циклов.
5. Граф G(V,X) связный , но утрачивает это свойство после удаления любого ребра.
Итак, дерево с n вершинами имеет n-1 ребро, поэтому оно будет минимальным связным графом.
Висячие вершины, за исключением корневой, называют листьями.
Остовом связного графа называется любой его подграф , содержащий все вершины графа и являющийся деревом.
Подграф G1 = (V1, E1) графа G = (V, E), называется остовным деревом в
графе G = (V, E), если G1 = (V1, E1) — дерево и V1 = V.
Источник
Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
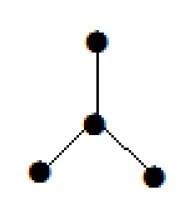
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
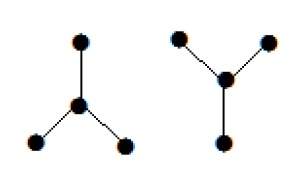
Охватывающие деревья
Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —
- H это дерево
- H содержит все вершины G.
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
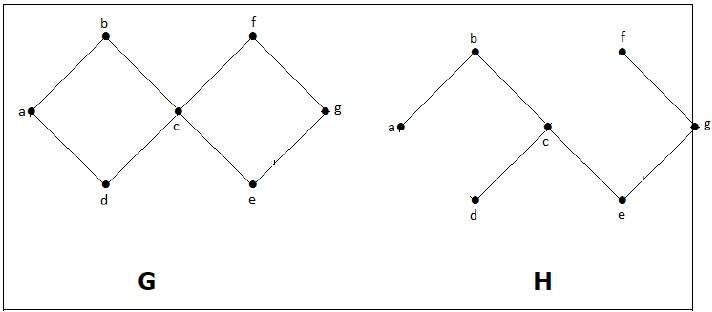
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H — остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
Посмотрите на следующий график —
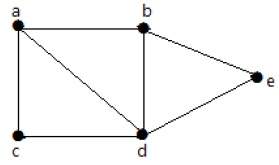
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
Тогда ранг цепи
G = m – (n – 1)
= 7 – (5 – 1)
= 3
пример
Пусть ‘G’ — связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
n ∑ i = 1 градус (V i ) = 2 | E |
6 × 3 = 2 | E |
| E | = 9
Схема ранг = | E | — (| V | — 1)
= 9 — (6 — 1) = 4
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
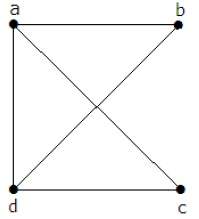
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
Сформулируем основные свойства деревьев.
Свойство 1.
Для каждой пары вершин дерева существует единственный путь, их соединяющий.
Этим свойством пользуются при нахождении всех предков, например, по мужской линии, любого человека, чья родословная представлена в виде генеалогического дерева, которое является «деревом» и в смысле теории графов. Например, на рисунке (являющегося деревом, вершины которого изображены прямоугольниками с помещенной в них информацией) представлено генеалогическое дерево некоего Максима.
Рис. 17
По этому дереву однозначно находится предок Максима в любом поколении по любой линии.
Свойство 2.
Всякое ребро в дереве является мостом. Действительно, после удаления любого ребра дерева, оно «распадается» на два дерева.
Рис. 18
Это легко видеть на рисунке, если удалить, например, ребро А5А6 или ребро А1А3, или ребро А4А10 (оставив «вторым деревом» вершину A10).
Теорема.
Дерево с n вершинами имеет n-1 ребро.
Доказательство.
Для дерева — изолированной вершины n=1 и ребер 0, что соответствует теореме (n–1 = 1–1 = 0). Если из графа «дерева», не являющегося изолированной вершиной, удалить одно ребро, то получается два дерева с теми же вершинами. Для получения трех деревьев нужно удалить два ребра; для получения четырех деревьев — три ребра и т. д. Наибольшее количество деревьев из графа с n вершинами можно получить n (n изолированных вершин), чего можно достичь, удалив n–1 ребро. ч. т. д.
Задача. В стране Древляндия 101 город, и некоторые из них соединены дорогами. При этом любые два города соединяет ровно один путь. Сколько в этой стране дорог?
Решение.
Из условия задачи следует, что граф дорог Древляндии – дерево. У этого дерева есть висячая вершина. Удалим ее вместе с ребром, которое из нее выходит. Оставшийся граф также является деревом. Поэтому у него есть висячая вершина, которую мы также удалим вместе с выходящим из нее ребром. Проделав эту операцию 100 раз, мы получим граф, состоящий из одной вершины (в котором, конечно, нет ребер). Поскольку каждый раз удалялось ровно одно ребро, то сначала их было 100.
Теперь рассмотрим остальные свойства деревьев. Сделаем это в виде совокупности утверждений, которые эквивалентны между собой (т.е. из любого утверждения следует любое другое).
Теорема 1. Пусть G(X, E) – неориентированный граф с p вершинами и q ребрами. Тогда следующие утверждения эквивалентны.
- 1. G есть дерево.
- 2. Любые две различные вершины x и y графа G соединены единственной простой цепью.
- 3. G – связный граф, утрачивающий это свойство при удалении любого из его ребер.
- 4. G – связный граф и:
p = q + 1.
5. G – ациклический граф и:
p = q + 1.
6. G – ациклический граф, причем если любые две его вершины x и y соединить ребром e, то в полученном графе будет ровно один простой цикл.
Для доказательства теоремы достаточно доказать следующую цепочку следствий: 1 > 2 > 3 > 4 > 5 > 6 > 1 , так как это означает, что из любого утверждения 1 – 6 выводится любое другое.
- 1 > 2 . Так как граф связен, то любые две его вершины можно соединить простой цепью. Пусть 1 и 2 – две различные простые цепи, соединяющие вершины x и y. Если цепи 1 и 2 не имеют общих вершин, за исключением вершин x и y, то есть простой цикл. Предположим, что цепи 1 и 2 имеют общие вершины, отличные от x и y. Пусть z – первая из таких вершин при движении от вершины x к вершине y и пусть 1 (x, z) и 2 (x, z) – части цепей 1 и 2, взятые от вершины x до вершины z. Тогда – простой цикл. Это противоречит тому, что граф ацикличен, и поэтому 1=2, т. е. утверждение 2 доказано.
- 2 > 3 . Граф G – связен, поскольку любые две его различные вершины x и y соединены простой цепью. Возьмем некоторое ребро графа e = (x, y). Согласно 2 простая цепь ={e} между вершинами x и y единственна. Если ребро e удалить, то вершины x и y будет невозможно соединить простой цепью, и полученный граф будет несвязным. Утверждение 3 доказано.
- 3 > 4 . По условию 3 граф связен. Соотношение:
p = q + 1
докажем по индукции. Если граф имеет две вершины и удовлетворяет 3 , то он выглядит так:
Рис. 19
В этом случае p = 2, q = 1 и соотношение:
p = q + 1
выполняется. Предположим теперь, что соотношение верно для всех графов, удовлетворяющих 3 и имеющих меньше, чем p вершин, и докажем его для графа G с p вершинами. Удалим из графа G произвольное ребро e. Тогда новый граф G? будет несвязным и будет состоять из двух связных компонент G1 и G2. По предположению индукции имеем:
p1 = q1 + 1,
p2 = q2 + 1,
где pi – число вершин компоненты Gi, qi – число ее ребер. Следовательно,
p = p1 + p2,
q = q1 + q2 + 1,
поэтому:
p = q1 + q2 + 2 = q + 1,
и свойство 4 доказано.
4 > 5 . Предположим, что граф G, удовлетворяющий 4 , имеет простой цикл длиной 1. Этот цикл содержит l вершин и l ребер. Для любой из p – l вершин, не принадлежащих циклу, существует инцидентное ей ребро, лежащее на кратчайшей цепи (т. е. цепи минимальной длины), идущей от данной вершины к некоторой вершине цикла. Все такие ребра попарно различны. Если вершины x1 и x2 инцидентны одному такому ребру e, то e = (x1, x2), и кратчайшая цепь 1 для вершины x1 проходит через вершину x2, а кратчайшая цепь 2 для вершины x2 проходит через вершину x1 (рис. 20). Это противоречит тому, что цепи 1 и 2 – кратчайшие. Общее число ребер q в графе G в этом случае не меньше, чем:
l + p – l = p,
т. е. q = p, что противоречит соотношению:
p = q + 1.
Отсюда следует, что G – ациклический граф, и утверждение 5 доказано.
Рис. 20
5 > 6 . Так как G – ациклический граф, то каждая его компонента связности Gi (i = 1, 2, …, k) является деревом. Для каждой компоненты Gi имеем в соответствии с 5:
pi = qi + 1,
откуда:
,
т. е.:
p = q + k.
С другой стороны,:
p = q + 1,
поэтому k = 1, т. е. граф G связен. Таким образом, G – дерево. Тогда (см. 2 ) любые две различные вершины x и y графа G соединены единственной простой цепью. Если добавить ребро между несмежными вершинами x и y, то оно образует с указанной цепью единственный простой цикл. Утверждение 6 доказано.
6 > 1 . По условию 6 G – ациклический граф. Если граф G не является связным, то возьмем вершины x и y из различных компонент связности графа G и соединим их ребром e. Построенный граф является, как и граф G, ациклическим. Это противоречит свойству G, поэтому G – связный граф, и свойство 1 доказано. Таким образом, доказана и теорема 1.
Определение, аналогичное дереву, можно ввести и для орграфа.
Определение 2. Орграф G(X, E) называется прадеревом или ориентированным деревом, растущим из корня x0, при следующих условиях:
- 1. Неориентированный граф G’, соответствующий графу G, является деревом.
- 2. Единственная простая цепь между x0 и любой другой вершиной x графа G’ является путем в орграфе G, идущим из вершины x0 в вершину x.
На рис. 21 изображено ориентированное дерево.
Рис. 21
В неориентированном графе G(X, E) вершина x называется концевой или висячей, если d(x) = 1, т. е. если этой вершине инцидентно единственное ребро e. Это ребро также называется концевым или висячим. С висячими вершинами связана следующая теорема.
Теорема 2. В любом дереве G(X, E) с p * 2 вершинами имеется не менее двух концевых вершин.
Доказательство. Пусть q – число ребер дерева G. В силу теоремы 1:
p = q + 1.
Кроме того, из теоремы 1.1 имеем:
Таким образом, получаем:
.(1)
Предположим, что x0 – единственная концевая вершина в дереве G. Тогда (x0) = 1, (x) 2, если x0. Отсюда:
.(2)
Неравенство (2) противоречит (1), поэтому либо концевых вершин нет, либо их по крайней мере две. Если концевых вершин в G нет, то (x) 2 для всех X. Тогда:
.(3)
Неравенство (3) тоже противоречит (1). Отсюда следует, что концевых вершин в G две или больше. Теорема доказана.
Важным является вопрос о том, сколько существует деревьев с заданным числом вершин. Для деревьев с помеченными вершинами (например пронумерованными) или для помеченных деревьев ответ на этот вопрос дает следующая теорема.
Источник
