Граф с какими свойствами называют деревом что такое корень дерева ветви листья
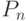
- 1
- 2
- 3
- 4
- 5
0.0/5, Голосов: 0
Задание 1. Что такое система; структура?
Система – объект, который состоит из взаимосвязанных элементов и существующий как единое целое.
Структура – определенный порядок объединения элементов, составляющих систему.
Задание 2. Назовите элементы, составляющие следующие системы: автомобиль, молекула воды, компьютер, магазин, Солнечная система, семья, футбольная команда, армия. Обоснуйте взаимозависимость элементов этих систем.
Автомобиль – двигатель, трансмиссия, рулевое управление, тормозная система, несущая система, подвеска и колёса.
Молекула воды – два атома водорода и один атом кислорода.
Компьютер – монитор, клавиатура, мышь, колонки и системный блок(материнская плата, жесткая и оперативная памяти, дисковод, блок питания, видеокарта и др.).
Магазин – касса, товар, полки, склад.
Солнечная система – планеты, карликовые планеты, спутники, малые тела и кометы.
Семья – родители и дети.
Футбольная команда – тренер, вратарь, защитник, полузащитник, нападающий, капитан, стартовый состав и запасные игроки.
Армия – солдаты, командир, оружие.
Задание 3. Что такое граф? Какую информацию он может нести в себе?
Граф – это совокупность объектов, связанные между собой линиями (связями), соединяющие вершины.
Задание 4. Как на графе изображаются элементы системы и отношения между ними?
Элементы системы – это вершины графа, которые изображаются овалами.
Отношения между элементами изображаются линиями, где направленная линия (со стрелкой) называется дугой, а если стрелки нет, то это ребро.
Задание 5. Что значит «симметричное отношение», «несимметричное отношение»? Как они изображаются на графе? Приведите примеры.
Симметричное отношение обозначает двустороннюю связь между элементами системы, которое изображается ненаправленной линией (ребром).
Примеры: муж и жена
Нессиметричное отношение обозначает одностороннюю связь между элементами системы, которое изображается направленной линией (дугой).
Примеры: Отец и сын, Неразделённая любовь
Задание 6. Дайте имена возможным связям между следующими объектами и изобразите связи между ними в форме графа: брат и сестра; ученик и школа; Саша и Маша; Москва и Париж; министр, директор, рабочий; Пушкин и Дантес; компьютер и процессор.
Симметричное отношение: брат – сестра; Саша – Маша; Москва – Париж.
Нессиметричное отношение: ученик директор –> рабочий; Пушкин процессор.
Задание 7. Граф с какими свойствами называют деревом? Что такое корень дерева, ветви, листья?
Дерево – это граф в котором нет петель, то есть связанных по замкнутой линии вершин. В направлении сверху вниз выполняется принцип «один ко многим».
Корень дерева – вершина нашего графа, в которую не ведут другие ребра.
Ветви – ребра дерева.
Листья – вершины, от которых не выходят ребра, то есть не имеют своих ветвей.
Задание 8. Какие системы называют иерархическими?
Иерархическая система называется системой, информационная модель которой представляется в виде дерева.
Задание 9. Можно ли систему файлов в Microsoft Windows (и подобных ей ОС) назвать иерархической? Какой смысл имеют связи между элементами этой системы? Что в ней является листьями, ветвями, корнем?
Да, можно. В этой системе файлов создаётся корневой каталог, в котором хранятся не только файлы, но и другие каталоги более низкого уровня (подкаталоги).
Листьями этого дерева являются файлы или подкаталоги, у которых нет своих ветвей. Корнем дерева является корневой каталог операционной системы. Ветвями являются стрелочки, по которым можно добраться до любого листа.
Задание 10. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения) — дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша.
Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?
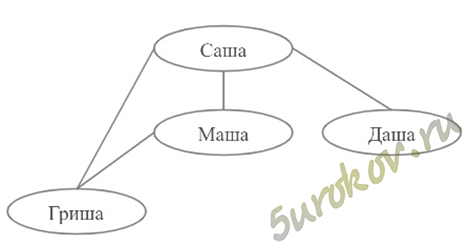
По графу можно понять, что Саша может поделиться секретом, не рискуя, только с Дашей, так как у нее нет никаких взаимоотношений между его друзьями Машей или Гришей. Маша и Гриша дружат и есть риск, что секрет кто-то из них расскажет.
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июня 2020; проверки требует 1 правка.
Дерево — это связный ациклический граф.[1] Связность означает наличие маршрута между любой парой вершин, ацикличность — отсутствие циклов. Отсюда, в частности, следует, что число рёбер в дереве на единицу меньше числа вершин, а между любыми парами вершин имеется один и только один путь.
Лес — множество деревьев.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.[2]
Связанные определения[править | править код]
- Степень вершины — количество инцидентных ей ребер.
- Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).
- Узел ветвления — неконцевой узел.
- Дерево с отмеченной вершиной называется корневым деревом.
- Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:
- уровень корня дерева равен 0;
- уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева , содержащего данный узел.
- Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
- Несводимым называется дерево, в котором нет вершин степени 2.
- Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
- Центроид — вершина, при удалении которой размеры получившихся компонент связности не превышают (половины размера исходного дерева)
Двоичное дерево[править | править код]
Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.
Термин двоичное дерево (применяется так же термин бинарное дерево) имеет несколько значений:
- Неориентированное дерево, в котором степени вершин не превосходят 3.
- Ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
- Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, как двоичное дерево поиска, двоичная куча, красно-чёрное дерево, АВЛ-дерево, фибоначчиева куча и др.
N-арные деревья[править | править код]
N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.
- N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
- N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.
Свойства[править | править код]
Подсчёт деревьев[править | править код]
для числа неизоморфных корневых деревьев с вершинами удовлетворяет функциональному уравнению
.
- Производящая функция
для числа неизоморфных деревьев с вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:
- При верна следующая асимптотика
где и определённые константы, , .
Кодирование деревьев[править | править код]
- Дерево можно задать в виде стpоки, содержащей символы, помечающие вершины деpева, а также открывающие и закрывающие кpуглые скобки. Между деpевьями и их линейными скобочными записями существует взаимно однозначное соответствие.
См. также[править | править код]
- Глоссарий теории графов
- Лес непересекающихся множеств
- Список структур данных (деревья)
Примечания[править | править код]
- ↑ § 13. Определение дерева // Лекции по теории графов / Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И.. — М.: Наука, Физматлит, 1990. — С. 53. — 384 с. — 22 000 экз. — ISBN 5-02-013992-0.
- ↑ Альфс Берзтисс. Глава 3. Теория графов. 3.6. Деревья // Структуры данных = A. T. Berztiss. Data structures. Theory and practice. — М.: Статистика, 1974. — С. 131. — 10 500 экз.
- ↑ Дискретная математика: алгоритмы. Формула Кэли (недоступная ссылка). Дата обращения: 29 октября 2009. Архивировано 14 июня 2009 года.
Литература[править | править код]
- Дональд Кнут. Искусство программирования, том = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 0-201-89683-4.
- Оре О. Теория графов. — 2-е изд. — М.: Наука, 1980. — 336 с.
- Харари Ф. Теория графов. — М.: Мир, 1973. — 302 с.
Источник
Аннотация: Деревья. Центр дерева. Корневые деревья. Каркасы. Двудольные графы.
Планарные графы.
Деревья
Деревом называется связный граф,
не имеющий циклов. В графе без
циклов, таким образом, каждая компонента связности является деревом.
Такой граф называют лесом.
Из теоремы 2
“Маршруты, связность, расстояния”
следует, что во всяком дереве, в котором не
меньше двух вершин, имеется вершина степени 1. Такие вершины называют висячими вершинами, или листьями. В действительности
легко
доказать, что в каждом дереве не меньше двух листьев, а цепь 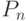 –
–
пример дерева, в котором точно два листа.
В следующих двух теоремах устанавливаются некоторые свойства деревьев.
Теорема 1. Граф с  вершинами и
вершинами и  ребрами является деревом
ребрами является деревом
тогда
и только тогда, когда он
удовлетворяет любым двум из следующих трех условий:
- (1) связен;
- (2) не имеет циклов;
- (3)
 .
.
Доказательство.
Первые два условия вместе составляют определение
дерева. Покажем, что выполнение любых двух из условий (1)-(3) влечет
за собой выполнение третьего.
(1) и (2)  (3). Индукция по числу вершин. При
(3). Индукция по числу вершин. При 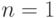
утверждение очевидно. При  в дереве имеется хотя бы один
в дереве имеется хотя бы один
лист.
Если из дерева удалить лист, то снова получится дерево, так как циклов не
появится, а связность, очевидно, сохранится. В этом новом дереве 
вершин и, по предположению индукции,  ребра. Следовательно,
ребра. Следовательно,
в исходном дереве было  ребро.
ребро.
(2) и (3)  (1). Пусть в графе, не имеющем циклов,
(1). Пусть в графе, не имеющем циклов, 
ребро, а его компонентами связности являются 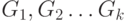 ,
,
причем 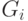 состоит из
состоит из 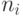 вершин,
вершин, 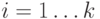 .
.
Каждая компонента является деревом, поэтому, как доказано выше, число
ребер в 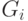 равно
равно 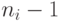 , а всего ребер в
, а всего ребер в
графе 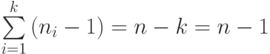 .
.
Значит, 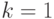 и граф связен.
и граф связен.
(1) и (3)  (2). Рассмотрим связный граф
(2). Рассмотрим связный граф
с  ребром.
ребром.
Если бы в нем был цикл, то, удалив любое цикловое ребро, мы получили бы
связный граф с меньшим числом ребер. Можно продолжать такое удаление ребер
до тех пор, пока не останется связный граф без циклов, то есть дерево.
Но ребер в этом дереве было бы меньше, чем  , а это противоречит
, а это противоречит
доказанному выше.
Теорема 2. Если  – дерево, то
– дерево, то
- в
 любая пара вершин соединена единственным
любая пара вершин соединена единственным
путем; - при добавлении к
 любого нового ребра образуется
любого нового ребра образуется
цикл; - при удалении из
 любого ребра он превращается
любого ребра он превращается
в несвязный граф.
Доказательство.
Существование пути между любыми двумя вершинами
следует из связности дерева. Допустим, что в некотором дереве существуют
два различных пути, соединяющих вершины  и
и  .
.
Начальные отрезки этих путей совпадают (оба пути начинаются в одной и той
же вершине  ). Пусть
). Пусть  – последняя вершина
– последняя вершина
этого совпадающего
начала, а после  в одном пути следует
в одном пути следует
вершина 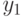 ,
,
а в другом – вершина 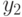 . Рассмотрим ребро
. Рассмотрим ребро 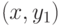 .
.
Если его удалить из графа, то в оставшемся подграфе вершины 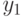
и  будут соединимыми – соединяющий их маршрут можно
будут соединимыми – соединяющий их маршрут можно
построить так:
взять отрезок первого пути от 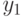 до
до  и к нему
и к нему
присоединить
отрезок второго от  до
до  , взятый в обратном
, взятый в обратном
порядке. Но это
означает, что ребро 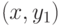 не является перешейком.
не является перешейком.
Однако из теоремы 4
“Маршруты, связность, расстояния”
следует, что в дереве каждое ребро
является перешейком. Этим доказано утверждение 1). Утверждения 2) и 3)
следуют из 1).
Отметим, что единственный путь, соединяющий две вершины дерева, всегда
простой (если путь не является простым, в нем обязательно содержится
цикл).
Источник
2. Назовите элементы, составляющие следующие системы: автомобиль, молекула воды, компьютер, магазин. Солнечная система, семья, футбольная команда, армия. Обоснуйте взаимозависимость элементов этих систем.
Автомобиль: кузов, двигатель, шасси (без чего-либо из этого автомобиль не поедет)
Молекула воды: два атома водорода, атом кислорода (атомы соединены химическими связями)
Компьютер: корпус, системная плата, периферийные устройства (корпус содержит системную плату, к системной плате прикрепляются периферийные устройства)
Магазин: продавцы, товар (продавцы продают товар)
Солнечная система: планеты, спутники планет, Солнце, кометы, астероиды, … (объекты действуют друг на друга гравитацией)
Семья: родители, дети, родственники мужа, родственники жены (все связаны родственными связями)
Футбольная команда: игроки, тренеры, обслуживающий персонал (тренер тренирует игроков, персонал поддерживает игроков, технику, поля в форме)
Армия: военные, оружие, техника (военные управляют оружием и техникой)
3. Что такое граф? Какую информацию он может нести в себе?
Граф – объект, содержащий набор вершин и рёбер, соединяющих вершины. Граф может содержать различную информацию о взаимоотношениях между объектами, например, маршруты между городами, родственные связи, результаты матчей и т.д.
4. Как на графе изображаются элементы системы и отношения между ними?
Элементы системы изображаются вершинами графа, взаимоотношения – рёбрами.
5. Что значит «симметричное отношение», «несимметричное отношение»? Как они изображаются на графе? Приведите примеры.
Симметричное отношение – такое, в котором оба объекта равноценны, т.е. если А находится в отношении с Б, то и Б находится в отношении с А. На графе симметричные отношения неориентированные рёбра и или пары противоположно направленных рёбер. Пример симметричного отношения: быть супругом, быть сестрой, давать в сумме с числом 1000.
Несимметричное отношение – отношение, не являющееся симметричным, на графе обозначается направленными рёбрами. Примеры: влюблённость, отношения порядка (например, «больше»).
6. Дайте имена возможным связям между следующими объектами и изобразите связи между ними в форме графа: брат и сестра; ученик и школа; Саша и Маша; Москва и Париж; министр, директор, рабочий; Пушкин и Дантес; компьютер и процессор.
Брат – сестра (родственники), школа -> ученик (местоположение), Саша – Маша (имена, оканчивающиеся на одинаковые буквы), Москва – Париж (города разных стран), министр -> директор -> рабочий (подчинение), Пушкин <- Дантес (кто умер позже), компьютер -> процессор (входит в состав)
7. Граф с какими свойствами называют деревом? Что такое корень дерева, ветви, листья?
Деревом называют связный граф без циклов. Корень дерева – вершина, не имеющая родителей, ветви – имеющая родителей и потомков, листья – не имеющие потомков.
8. Какие системы называют иерархическими?
Отношения между элементами которых можно представить в виде дерева.
9. Можно ли систему файлов в MS Windows (и ей подобных) назвать иерархической? Какой смысл имеют связи между ее элементами? Что в ней является листьями, ветвями, корнем?
Можно, отношение – «находится в», листья – файлы, ветви – папки, корень – диск или «Мой компьютер»
10. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения):
дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша.
Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?
С Дашей, Маша и Гриша дружат друг с другом и могут проболтаться.
Источник
Корневые деревья
Произвольно зафиксируем
некоторую вершину дерева
и назовем
ее корнем дерева. Само дерево в этом случае будем называть деревом
с корнем или корневым деревом.
Иногда полезно, руководствуясь
какими–либо соображениями, выделять в дереве некоторую определенную цепь , которую обычно называют
стволом дерева. Корень дерева обычно является одной из концевых
вершин ствола. Каждая концевая вершина дерева связана с ближайшей вершиной ствола единственной цепью.
Эту цепь называют ветвью дерева, выходящей из вершины в вершину . При отсутствии у дерева
ствола, ветвями дерева называют цепи, связывающие концевые вершины дерева
с его корнем.
Корневые деревья естественно
ориентировать, если в этом есть необходимость, от корня. Все
ребра, инцидентные корню дерева, считаются исходящими из корня и заходящими
в вершины, смежные корню. Все ребра дерева, инцидентные вершинам, удаленным
на расстояние 1 от корня, считаются исходящими из этих вершин и заходящими
в вершины, им смежные. Процесс ориентации ребер продолжается подобным
образом до тех пор, пока не будут ориентированы все ребра дерева. Поученное
в результате такой ориентации дерево с корнем называется ориентированным
деревом. В нем все ребра имеют направление от корня. Если поменять
направления всех дуг ориентированного дерева на противоположные (к
корню), то получившийся в итоге ориентированный граф называют
сетью сборки.
На рис. 4. 38 приведены примеры дерева
с корнем ,
его ориентированного дерева и сети сборки .
Деревья графов
Пусть дерево является подграфом графа
.
Ребра графа , которые принадлежат дереву
,
называются ветвями дерева ,
а ребра, не принадлежащие дереву , –
хордами относительно дерева . Если есть суграф , то есть вершины дерева совпадают с вершинами графа , то говорят, что дерево
покрывает граф . В этом случае дерево называют остовом
или каркасом графа .
Существует простой способ определить количество
различных остовов мультиграфа с вершинами. Для этого нужно записать матрицу
размера
, по главной диагонали которой
выписаны степени вершин, а элементы равны взятому со знаком минус числу ребер,
связывающих вершины и
,
.
Вычислив минор любого элемента главной диагонали матрицы , получим искомое число возможных
остовов графа.
Например, для графа на рис. 4.39 имеем:
; .
Следовательно, существует
50 различных деревьев, покрывающих этот граф. Один из 50 остовов мультиграфа
изображен на рис. 4.39 жирными линиями.
Экстремальные графы
Класс практических задач, достаточно успешно решаемых
методами теории графов, требует связать пунктов наиболее экономичным образом. Например,
необходимо построить автомобильные дороги, связывающие дачных поселков, так, чтобы
их суммарная длина была наименьшей. Любые два поселка должны быть
связаны дорогой либо непосредственно, либо дорогами, проходящими через
другие поселки. Похожие задачи возникают при прокладке водопроводов,
газопроводов, линий связи и т. п.
На языке теории графов задачи такого рода формулируются
следующим образом. Каждому ребру полного графа с вершинами приписывается вес , выражающий численно расстояние,
стоимость или иную величину, характеризующую взаимосвязь между каждой
парой вершин графа. Требуется выявить такой остов этого графа, чтобы
суммарный вес ветвей остова был минимальным (или
максимальным). Такой остов графа называют его экстремальным
деревом.
Поскольку полный граф покрывает различных основных деревьев, то
решение этой задачи полным перебором вариантов потребовало бы чрезвычайно
больших вычислений даже при относительно малых . Уже при таких вариантов больше миллиона.
Для решения задач такого рода разработаны достаточно
эффективные алгоритмы. Далее мы воспользуемся одним из них – алгоритмом Дж. Краскала. Его суть состоит в следующем. На первом шаге выбирается
первая ветвь искомого остова – это ребро графа с
наименьшим (наибольшим) весом. Затем на каждом следующем шаге рассматривается
минимальное (максимальное) по весу ребро и, если оно не образует цикла
с ранее выбранными ветвями, вводится в остов. Построение заканчивается
после отбора для остова ребер.
Теорема 4.13. Алгоритм Краскала позволяет построить экстремальный
граф любого связного графа.
Пример 4.3. Необходимо построить автомобильные дороги, связывающие
девять поселков так, чтобы их суммарная длина была наименьшей. Любые
два поселка должны быть связаны дорогой либо непосредственно, либо
дорогами, проходящими через другие поселки. Известно расстояние между
поселками (в км):
На первом шаге выбираем самый короткий участок искомой сети дорог, связывающей
поселки. Это дорога длиною 12 км между поселками П1 и П2. Затем добавляем
к ней дороги между П1 и П3 (13 км), П1 и П9 (14 км), П5 и П7 (15 км),
П3 и П4 (18 км). Следующее минимальное расстояние между поселками
равно 19 км. Таково расстояние между П1 и П8 и между П6 и П7. Так
как обе эти дороги не образуют цикла с уже отобранными дорогами, то
обе они добавляются в список. Следующие по длине (25 км и 26 км) дороги
между П1, П2 и П5, П6 нельзя добавлять в наш список – иначе появятся циклы: П1, П2, П3, П2 или П5, П6, П7,
П5. Восьмая и последняя дорога искомого минимального остова имеет
длину 28 км, она проходит между П5 и П8. Минимальный остов, связывающий
девять поселков, изображен на рис. 4.40. Минимальная длина дорог, связывающих поселки, равна
138 км.
Рис.4.40
Экстремальное дерево может быть построено для произвольного графа, а не
только для полного графа. Например, связи между некоторыми вершинами
могут быть нежелательными или недопустимыми.
Источник
