Граф с какими свойствами называют деревом
- 1
- 2
- 3
- 4
- 5
0.0/5, Голосов: 0
Задание 1. Что такое система; структура?
Система – объект, который состоит из взаимосвязанных элементов и существующий как единое целое.
Структура – определенный порядок объединения элементов, составляющих систему.
Задание 2. Назовите элементы, составляющие следующие системы: автомобиль, молекула воды, компьютер, магазин, Солнечная система, семья, футбольная команда, армия. Обоснуйте взаимозависимость элементов этих систем.
Автомобиль – двигатель, трансмиссия, рулевое управление, тормозная система, несущая система, подвеска и колёса.
Молекула воды – два атома водорода и один атом кислорода.
Компьютер – монитор, клавиатура, мышь, колонки и системный блок(материнская плата, жесткая и оперативная памяти, дисковод, блок питания, видеокарта и др.).
Магазин – касса, товар, полки, склад.
Солнечная система – планеты, карликовые планеты, спутники, малые тела и кометы.
Семья – родители и дети.
Футбольная команда – тренер, вратарь, защитник, полузащитник, нападающий, капитан, стартовый состав и запасные игроки.
Армия – солдаты, командир, оружие.
Задание 3. Что такое граф? Какую информацию он может нести в себе?
Граф – это совокупность объектов, связанные между собой линиями (связями), соединяющие вершины.
Задание 4. Как на графе изображаются элементы системы и отношения между ними?
Элементы системы – это вершины графа, которые изображаются овалами.
Отношения между элементами изображаются линиями, где направленная линия (со стрелкой) называется дугой, а если стрелки нет, то это ребро.
Задание 5. Что значит «симметричное отношение», «несимметричное отношение»? Как они изображаются на графе? Приведите примеры.
Симметричное отношение обозначает двустороннюю связь между элементами системы, которое изображается ненаправленной линией (ребром).
Примеры: муж и жена
Нессиметричное отношение обозначает одностороннюю связь между элементами системы, которое изображается направленной линией (дугой).
Примеры: Отец и сын, Неразделённая любовь
Задание 6. Дайте имена возможным связям между следующими объектами и изобразите связи между ними в форме графа: брат и сестра; ученик и школа; Саша и Маша; Москва и Париж; министр, директор, рабочий; Пушкин и Дантес; компьютер и процессор.
Симметричное отношение: брат – сестра; Саша – Маша; Москва – Париж.
Нессиметричное отношение: ученик директор –> рабочий; Пушкин процессор.
Задание 7. Граф с какими свойствами называют деревом? Что такое корень дерева, ветви, листья?
Дерево – это граф в котором нет петель, то есть связанных по замкнутой линии вершин. В направлении сверху вниз выполняется принцип «один ко многим».
Корень дерева – вершина нашего графа, в которую не ведут другие ребра.
Ветви – ребра дерева.
Листья – вершины, от которых не выходят ребра, то есть не имеют своих ветвей.
Задание 8. Какие системы называют иерархическими?
Иерархическая система называется системой, информационная модель которой представляется в виде дерева.
Задание 9. Можно ли систему файлов в Microsoft Windows (и подобных ей ОС) назвать иерархической? Какой смысл имеют связи между элементами этой системы? Что в ней является листьями, ветвями, корнем?
Да, можно. В этой системе файлов создаётся корневой каталог, в котором хранятся не только файлы, но и другие каталоги более низкого уровня (подкаталоги).
Листьями этого дерева являются файлы или подкаталоги, у которых нет своих ветвей. Корнем дерева является корневой каталог операционной системы. Ветвями являются стрелочки, по которым можно добраться до любого листа.
Задание 10. Нарисуйте в виде графа систему, состоящую из четырех одноклассников, между которыми существуют следующие связи (взаимоотношения) — дружат: Саша и Маша, Саша и Даша, Маша и Гриша, Гриша и Саша.
Глядя на полученный граф, ответьте на вопрос: с кем Саша может поделиться секретом, не рискуя, что он станет известен кому-то другому?
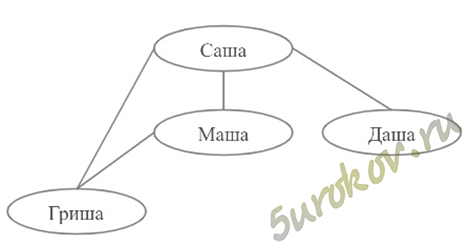
По графу можно понять, что Саша может поделиться секретом, не рискуя, только с Дашей, так как у нее нет никаких взаимоотношений между его друзьями Машей или Гришей. Маша и Гриша дружат и есть риск, что секрет кто-то из них расскажет.
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 июня 2020; проверки требует 1 правка.
Дерево — это связный ациклический граф.[1] Связность означает наличие маршрута между любой парой вершин, ацикличность — отсутствие циклов. Отсюда, в частности, следует, что число рёбер в дереве на единицу меньше числа вершин, а между любыми парами вершин имеется один и только один путь.
Лес — множество деревьев.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.[2]
Связанные определения[править | править код]
- Степень вершины — количество инцидентных ей ребер.
- Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).
- Узел ветвления — неконцевой узел.
- Дерево с отмеченной вершиной называется корневым деревом.
- Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:
- уровень корня дерева равен 0;
- уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева , содержащего данный узел.
- Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
- Несводимым называется дерево, в котором нет вершин степени 2.
- Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
- Центроид — вершина, при удалении которой размеры получившихся компонент связности не превышают (половины размера исходного дерева)
Двоичное дерево[править | править код]
Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.
Термин двоичное дерево (применяется так же термин бинарное дерево) имеет несколько значений:
- Неориентированное дерево, в котором степени вершин не превосходят 3.
- Ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
- Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, как двоичное дерево поиска, двоичная куча, красно-чёрное дерево, АВЛ-дерево, фибоначчиева куча и др.
N-арные деревья[править | править код]
N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.
- N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
- N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.
Свойства[править | править код]
Подсчёт деревьев[править | править код]
для числа неизоморфных корневых деревьев с вершинами удовлетворяет функциональному уравнению
.
- Производящая функция
для числа неизоморфных деревьев с вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:
- При верна следующая асимптотика
где и определённые константы, , .
Кодирование деревьев[править | править код]
- Дерево можно задать в виде стpоки, содержащей символы, помечающие вершины деpева, а также открывающие и закрывающие кpуглые скобки. Между деpевьями и их линейными скобочными записями существует взаимно однозначное соответствие.
См. также[править | править код]
- Глоссарий теории графов
- Лес непересекающихся множеств
- Список структур данных (деревья)
Примечания[править | править код]
- ↑ § 13. Определение дерева // Лекции по теории графов / Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И.. — М.: Наука, Физматлит, 1990. — С. 53. — 384 с. — 22 000 экз. — ISBN 5-02-013992-0.
- ↑ Альфс Берзтисс. Глава 3. Теория графов. 3.6. Деревья // Структуры данных = A. T. Berztiss. Data structures. Theory and practice. — М.: Статистика, 1974. — С. 131. — 10 500 экз.
- ↑ Дискретная математика: алгоритмы. Формула Кэли (недоступная ссылка). Дата обращения: 29 октября 2009. Архивировано 14 июня 2009 года.
Литература[править | править код]
- Дональд Кнут. Искусство программирования, том = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 0-201-89683-4.
- Оре О. Теория графов. — 2-е изд. — М.: Наука, 1980. — 336 с.
- Харари Ф. Теория графов. — М.: Мир, 1973. — 302 с.
Источник
Деревья — это графики, которые не содержат ни одного цикла. Они представляют иерархическую структуру в графической форме. Деревья относятся к простейшему классу графов. Несмотря на их простоту, они имеют богатую структуру.
Деревья предоставляют целый ряд полезных приложений, от простого семейного дерева до сложных в структурах данных компьютерной науки.
дерево
Связный ациклический граф называется деревом. Другими словами, связный граф без циклов называется деревом.
Края дерева известны как ветви . Элементы деревьев называются их узлами . Узлы без дочерних узлов называются листовыми узлами .
Дерево с ‘n’ вершинами имеет ‘n-1’ ребер. Если у него есть еще одно ребро, превышающее ‘n-1’, то это дополнительное ребро, очевидно, должно соединиться с двумя вершинами, что приводит к образованию цикла. Затем он становится циклическим графом, что является нарушением для графа дерева.
Пример 1
График, показанный здесь, является деревом, потому что у него нет циклов, и он связан. Он имеет четыре вершины и три ребра, т. Е. Для ‘n’ вершин ‘n-1’ ребер, как указано в определении.
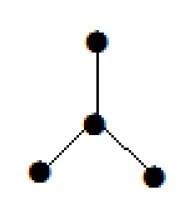
Примечание. Каждое дерево имеет как минимум две вершины первой степени.
Пример 2
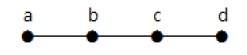
В приведенном выше примере вершины «a» и «d» имеют степень один. А две другие вершины ‘b’ и ‘c’ имеют второй уровень. Это возможно, потому что для того, чтобы не формировать цикл, в диаграмме должно быть как минимум два отдельных ребра. Это не что иное, как два ребра со степенью один.
лес
Несвязный ациклический граф называется лесом. Другими словами, непересекающаяся коллекция деревьев называется лесом.
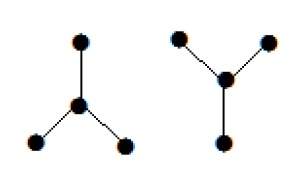
пример
Следующий график выглядит как два подграфа; но это один несвязный граф. На этом графике нет циклов. Отсюда ясно, что это лес.
Охватывающие деревья
Пусть G — связный граф, тогда подграф H в G называется остовным деревом в G, если —
- H это дерево
- H содержит все вершины G.
Остовное дерево T неориентированного графа G является подграфом, который включает в себя все вершины G.
пример
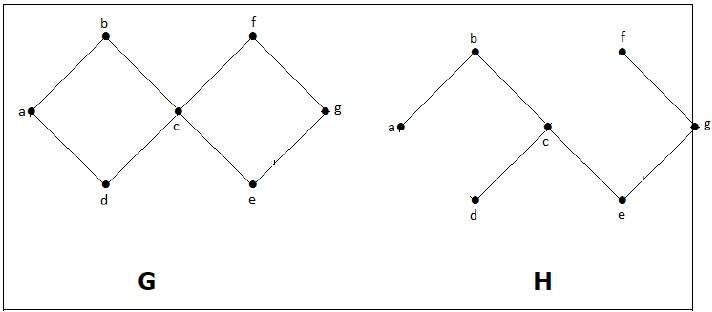
В приведенном выше примере G является связным графом, а H является подграфом G.
Ясно, что граф H не имеет циклов, это дерево с шестью ребрами, которое на единицу меньше общего числа вершин. Следовательно, H — остовное дерево группы G.
Circuit Rank
Пусть «G» связный граф с «n» вершинами и «m» ребрами. Остовное дерево ‘T’ группы G содержит (n-1) ребер.
Следовательно, количество ребер, которые нужно удалить из ‘G’, чтобы получить остовное дерево = m- (n-1), которое называется рангом схемы G.
Эта формула верна, потому что в остовном дереве вам нужно иметь ребра n-1. Из «m» ребер вам нужно сохранить «n – 1» ребер в графе.
Следовательно, удаление ребер n – 1 из m дает ребра, которые нужно удалить из графа, чтобы получить остовное дерево, которое не должно образовывать цикл.
пример
Посмотрите на следующий график —
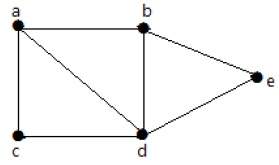
Для графика, приведенного в примере выше, у вас есть m = 7 ребер и n = 5 вершин.
Тогда ранг цепи
G = m – (n – 1)
= 7 – (5 – 1)
= 3
пример
Пусть ‘G’ — связный граф с шестью вершинами, а степень каждой вершины равна трем. Найдите звание цепи «G».
По сумме теоремы о степени вершин
n ∑ i = 1 градус (V i ) = 2 | E |
6 × 3 = 2 | E |
| E | = 9
Схема ранг = | E | — (| V | — 1)
= 9 — (6 — 1) = 4
Теорема Кирхгофа
Теорема Кирхгофа полезна для нахождения числа связующих деревьев, которые могут быть сформированы из связного графа.
пример
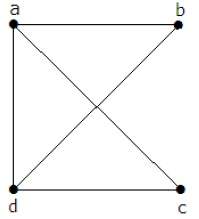
Матрица «А» заполняется так, как если между двумя вершинами есть ребро, то она должна быть задана как «1», иначе «0».
Источник
Дерево — это связный ациклический граф.[1] Связность означает наличие путей между любой парой вершин, ацикличность — отсутствие циклов и то, что между парами вершин имеется только по одному пути.
Лес — упорядоченное множество упорядоченных деревьев.
Ориентированное (направленное) дерево — ацикличный орграф (ориентированный граф, не содержащий циклов), в котором только одна вершина имеет нулевую степень захода (в неё не ведут дуги), а все остальные вершины имеют степень захода 1 (в них ведёт ровно по одной дуге). Вершина с нулевой степенью захода называется корнем дерева, вершины с нулевой степенью исхода (из которых не исходит ни одна дуга) называются концевыми вершинами или листьями.[2]
Связанные определения
- Степень вершины — количество инцидентных ей ребер.
- Концевой узел (лист, терминальная вершина) — узел со степенью 1 (то есть узел, в который ведёт только одно ребро; в случае ориентированного дерева — узел, в который ведёт только одна дуга и не исходит ни одной дуги).
- Узел ветвления — неконцевой узел.
- Дерево с отмеченной вершиной называется корневым деревом.
- Уровень узла — длина пути от корня до узла. Можно определить рекурсивно:
- уровень корня дерева равен 0;
- уровень любого другого узла на единицу больше, чем уровень корня ближайшего поддерева дерева , содержащего данный узел.
- Остовное дерево (остов) — это подграф данного графа, содержащий все его вершины и являющийся деревом. Рёбра графа, не входящие в остов, называются хордами графа относительно остова.
- Несводимым называется дерево, в котором нет вершин степени 2.
- Лес — множество (обычно упорядоченное), не содержащее ни одного непересекающегося дерева или содержащее несколько непересекающихся деревьев.
Двоичное дерево
Простое бинарное дерево размера 9 и высоты 3, с корнем значения 2. Это дерево не сбалансировано и не отсортировано.
Термин двоичное дерево (применяется так же термин бинарное дерево) имеет несколько значений:
- Неориентированное дерево, в котором степени вершин не превосходят 3.
- Ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят 2.
- Абстрактная структура данных, используемая в программировании. На двоичном дереве основаны такие структуры данных, как двоичное дерево поиска, двоичная куча, красно-чёрное дерево, АВЛ-дерево, фибоначчиева куча и др.
N-арные деревья
N-арные деревья определяются по аналогии с двоичным деревом. Для них также есть ориентированные и неориентированные случаи, а также соответствующие абстрактные структуры данных.
- N-арное дерево (неориентированное) — это дерево (обычное, неориентированное), в котором степени вершин не превосходят N+1.
- N-арное дерево (ориентированное) — это ориентированное дерево, в котором исходящие степени вершин (число исходящих рёбер) не превосходят N.
Свойства
Подсчёт деревьев
для числа неизоморфных корневых деревьев с вершинами удовлетворяет функциональному уравнению
.
- Производящая функция
для числа неизоморфных деревьев с вершинами можно представить с помощью перечисляющего ряда для корневых деревьев:
- При верна следующая асимптотика
где и определённые константы, , .
Кодирование деревьев
- Дерево можно задать набором скобок где пара скобок соответствует одной вершине, которые соединены ребром если соответствующие скобки непосредственно одна в другой. Например дерево на рисунке можно записать как ((()()(()))), взяв корень вершину 1, или (()()()(())), взяв за корень вершину 4.
См. также
- Глоссарий теории графов
- Лес непересекающихся множеств
- Список структур данных (деревья)
Примечания
- ↑ § 13. Определение дерева // Лекции по теории графов / Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И.. — М.: Наука, Физматлит, 1990. — С. 53. — 384 с. — 22 000 экз. — ISBN 5-02-013992-0.
- ↑ Альфс Берзтисс. Глава 3. Теория графов. 3.6. Деревья // Структуры данных = A. T. Berztiss. Data structures. Theory and practice. — М.: Статистика, 1974. — С. 131. — 10 500 экз.
- ↑ Дискретная математика: алгоритмы. Формула Кэли
Литература
- Дональд Кнут. Искусство программирования, том = The Art of Computer Programming, vol. 1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — Т. 1. Основные алгоритмы. — 720 с. — ISBN 0-201-89683-4.
- Оре О. Теория графов. — 2-е изд. — М.: Наука, 1980. — 336 с.
- Харари Ф. Теория графов. — М.: Мир, 1973. — 302 с.
Источник
4.3. Деревья и лес
Свойства деревьев
Определение 4.12. Граф
называется
деревом, если он связный и не имеет циклов.
Лесом называют граф, связные компоненты которого являются деревьями.
В частности, дерево не может иметь петель и кратных ребер.
Вершину графа, инцидентную только одному его ребру,
называют концевой (или висячей) вершиной,
а ребро, инцидентное концевой вершине, будем называть концевым ребром
графа.
Среди различных деревьев выделяют два важных частных
случая: последовательное дерево, представляющее собой простую
цепь, и звездное дерево (или куст), в котором одна из вершин
(центр) смежна со всеми остальными вершинами.
Пусть множество содержит вершин. Связав эти вершины
ребрами так, чтобы отсутствовали циклы, получим некоторое дерево, покрывающее
данное множество вершин. Для двух вершин существует одно покрывающее дерево
– сами вершины и ребро, их связывающее. С увеличением
число различных
деревьев быстро
увеличивается:
.
Деревья считаются существенно
различными, если они не изоморфны. Всего деревьев с четырьмя вершинами
16, из них существенно различных только 2; деревьев с шестью вершинами 1296,
а существенно различных всего 6, но уже при насчитывается около миллиона существенно различных
деревьев.. На рис. 4.34 приведены существенно различные деревья с четырьмя и
с шестью вершинами:
Среди графов n-го порядка (с n вершинами) без кратных
ребер полный граф имеет наибольшее количество ребер, а дерево
(n-го порядка) – наименьшее. Дерево содержит минимальное количество
ребер, необходимое для того, чтобы граф был связным.
Теорема 4.9. Каждое
дерево с вершинами
имеет в точности ребро.
► Действительно, две
вершины связываются одним ребром, и для связи каждой добавляемой вершины с
одной из уже имеющихся вершин необходимо еще одно ребро. Если же добавить
два ребра, то есть соединить новую вершину с двумя вершинами, из уже рассмотренных
вершин, то обязательно образуется цикл. Следовательно, для минимальной связи
вершин необходимо
и достаточно ребер. ◄
Нетрудно убедиться в справедливости
следующих теорем.
Теорема 4.10. Граф
является деревом тогда и только тогда, когда каждая пара различных вершин
графа соединяется одной и только одной простой цепью.
Теорема 4.11. У
каждого дерева найдется висячая вершина.
Теорема 4.12. При
удалении любого ребра дерева
оно распадается на связные компоненты, являющиеся либо изолированными вершинами,
либо деревьями. При добавлении в дерево любого нового ребра в нем образуется
простой цикл, и оно перестает быть деревом.
Дерево на рис. 4. 35 при
удалении ребра распадается
на лес из двух деревьев и , а после добавления ребра превращается в циклический
граф .
Рассматриваются также
деревья с ориентированными ребрами (дугами). Ориентированное дерево называется
прадеревом с корнем ,
если существует простой путь между вершиной и любой
другой его вершиной (рис. 4.36). Прадерево может иметь только один корень.
Типы вершин
дерева и его центры
Рассмотрим
дерево с
вершинами. Назовем его
концевые вершины вершинами типа 1. Теперь удалим все вершины типа
1 и концевые ребра. В результате получим связный граф без циклов , то есть опять дерево,
но с уже меньшим количеством вершин. Концевые вершины дерева назовем вершинами типа
2 в дереве .
Аналогично определяются вершины типов 3, 4 и т. д. Легко видеть, что дерево
может иметь либо одну вершину максимального типа, либо две таких вершины.
Типы вершин дерева ,
изображенного на рис. 4. 37, записаны рядом
с соответствующими вершинами. Здесь же показаны последовательные этапы процедуры,
позволяющей их определить. Это дерево имеет две вершины максимального типа.
Если у дерева удалить
одну из вершин типа 2 и ребра, ей инцидентные, то получившееся при этом
дерево будет иметь уже только одну вершину максимального типа.
Пусть вершина типа k
есть вершина максимального
типа. Из определения типа вершин дерева следует, что эксцентриситет
единственной вершины максимального типа равен ее типу, то есть равен
k, а
эксцентриситет каждой из двух вершин максимального типа равен k-1. При этом эксцентриситет
любой вершины не максимального типа будет обязательно больше. Поэтому
центрами любого дерева являются его вершины максимального типа, следовательно,
дерево имеет либо один, либо два центра. Нетрудно убедиться, что диаметральные
цепи в деревьях проходят через его центр или через оба центра, если
их два. В первом случае длина диаметральной цепи равна
2k-2, а во втором 2k-1.
Источник
