Функции у корень из х ее свойства и график какой график
Основные цели:
1) сформировать представление о
целесообразности обобщённого исследования
зависимостей реальных величин на примере
величин, связанных отношением у=
2) формировать способность к построению графика
у= и его
свойства;
3) повторить и закрепить приёмы устных и
письменных вычислений, возведение в квадрат,
извлечение квадратного корня.
Оборудование, демонстрационный материал: раздаточный
материал.
1. Алгоритм:

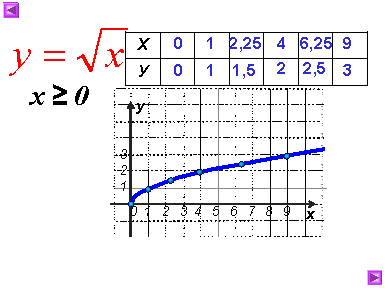
2. Образец для выполнения задания в группах:
3. Образец для самопроверки самостоятельной
работы:
4. Карточка для этапа рефлексии:
1) Я понял, как построить график функции у=.
2) Я могу по графику перечислить его свойства.
3) Я не допустил ошибок в самостоятельной
работе.
4) Я допустил ошибки в самостоятельной работе
(перечислить эти ошибки и указать их причину).
Ход урока
1. Самоопределение к учебной деятельности
Цель этапа:
1) включить учащихся в учебную деятельность;
2) определить содержательные рамки урока:
продолжаем работать с действительными числами.
Организация учебного процесса на этапе 1:
– Что мы изучали на прошлом уроке? (Мы изучали
множество действительных чисел, действия с ними,
построили алгоритм для описания свойств функции,
повторяли функции изученные в 7 классе).
– Сегодня мы продолжим работать с множеством
действительных чисел, функцией.
2. Актуализация знаний и фиксация затруднений в
деятельности
Цель этапа:
1) актуализировать учебное содержание,
необходимое и достаточное для восприятия нового
материала: функция, независимая переменная,
зависимая переменна, графики
y = kx + m, y = kx, y =c, y =x2, y = – x2 ,
2) актуализировать мыслительные операции,
необходимые и достаточные для восприятия нового
материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и
алгоритмы в виде схем и символов;
4) зафиксировать индивидуальное затруднение в
деятельности, демонстрирующее на личностно
значимом уровне недостаточность имеющихся
знаний.
Организация учебного процесса на этапе 2:
1. Давайте вспомним как можно задать
зависимости между величинами? (С помощью текста,
формулы, таблицы, графика)
2. Что называется функцией? (Зависимость между
двумя величинами, где каждому значению одной
переменной соответствует единственное значение
другой переменной y = f(x)).
Как называется х? (Независимая переменная –
аргумент)
Как называется у? (Зависимая переменная).
3. В 7- м классе мы изучили функции? (y = kx + m, y = kx, y =c,
y =x2, y = – x2 , ).
Индивидуальное задание:
Что является графиком функций y = kx + m, y =x2, y
= ?
3. Выявление причин затруднений и постановка
цели деятельности
Цель этапа:
1) организовать коммуникативное
взаимодействие, в ходе которого выявляется и
фиксируется отличительное свойство задания,
вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
Организация учебного процесса на этапе 3:
– Что особенного в этом задании? (Зависимость
задана формулой y = с которой мы еще не встречались).
– Какая цель урока? (Познакомиться с функцией y =
, ее
свойствами и графиком. Функцией в таблице
определять вид зависимости, строить формулу и
график.)
– Можно сформулировать тему урока? (Функция у=, ее свойства и
график).
– Запишите тему в тетради.
4. Построение проекта выхода из затруднения
Цель этапа:
1) организовать коммуникативное взаимодействие
для построения нового способа действия,
устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в
знаковой, вербальной форме и с помощью эталона.
Организация учебного процесса на этапе 4:
Работу на этапе можно организовать по группам,
предложив группам построить график y = , затем
проанализировать получившиеся результаты. Также
группам можно предложить по алгоритму описать
свойства данной функции.
5. Первичное закрепление во внешней речи
Цель этапа: зафиксировать изученное
учебное содержание во внешней речи.
Организация учебного процесса на этапе 5:
Постройте график у= – и опишите его свойства.
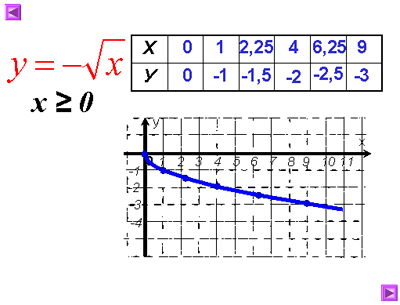
Свойства у= – .
1.Область определения функции.
D(y) =
2.Область значений функции.
E(y) =
3. y = 0, y> 0, y<0.
y =0, если x = 0.
y<0, если х(0;+)
4.Возрастания, убывания функции.
Функция убывает при х [0;+ )
5. Ограниченность функции.
Функция ограничена сверху, и не ограничена
снизу.
6.Наибольшее, наименьшее значения функции.
у наиб. = нет у наим. = 0.
7.Непрерывность функции.
Функция непрерывна на все области определения.
№13.2(в)
Используя график функции у=, найдите наименьшее и
наибольшее значения функции на отрезке [1; 9].
Построим график у=.
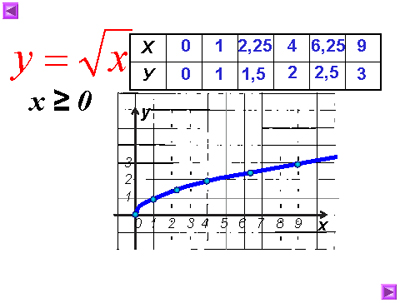
Выделим его часть на отрезке [1;9]. Заметим, что у наим.
= 1 при х = 1, а у наиб. =3 при х = 9.
Ответ: у наим. = 1, у наиб. =3
6. Самостоятельная работа с самопроверкой по
эталону
Цель этапа: проверить своё умение
применять новое учебное содержание в типовых
условиях на основе сопоставления своего решения
с эталоном для самопроверки.
Организация учебного процесса на этапе 6:
№ 13.1(в)
Учащиеся выполняют задание самостоятельно,
проводят самопроверку по эталону, анализируют,
исправляют ошибки.
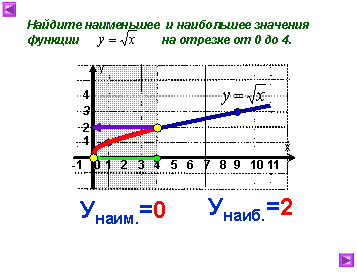
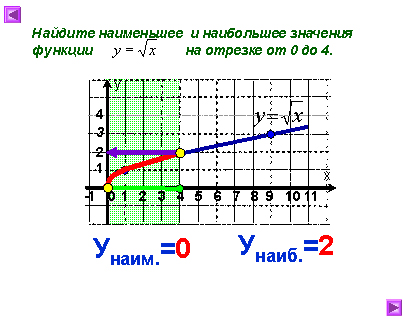
Построим график у=.
С помощью графика найдите наименьшее и
наибольшее значения функции на отрезке [0; 4].
7. Включение в систему знаний и повторение
Цель этапа: тренировать навыки
использования нового содержания совместно с
ранее изученным: 2) повторить учебное содержание,
которое потребуется на следующих уроках.
Организация учебного процесса на этапе 7:
Решите графически уравнение: = х – 6.
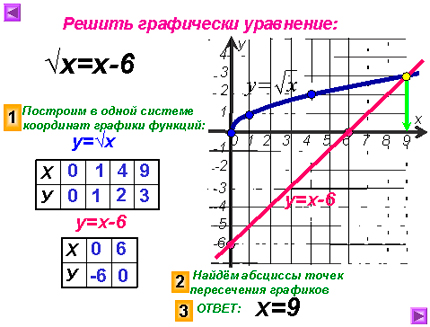
Ответ: 9.
Один ученик у доски остальные в тетрадях.
8. Рефлексия деятельности
Цель этапа:
1) зафиксировать новое содержание, изученное на
уроке;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые
помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как
направления будущей учебной деятельности;
5) обсудить и записать домашнее задание.
Организация учебного процесса на этапе 8:
– Ребята, какая цель стояла сегодня перед нами?
(Изучить функцию у=, ее свойства и график).
– Какие знания нам помогли в достижении цели?
(Умение искать закономерности, умение читать
графики.)
– Проанализируйте свою деятельность на уроке.
(Карточки с рефлексией)
Домашнее задание
п. 13 (до примера 2) № 13.3, 13.4
Решите графически уравнение:
Постройте график функции и опишите его
свойства:
Источник
Поурочное планирование по алгебре для 8 класса. Ориентировано на работу с УМК Макарычев. Алгебра 8 класс. Просвещение. Глава 2. КВАДРАТНЫЕ КОРНИ (19 ч). § 5. Арифметический квадратный корень (5 ч). Уроки 29, 30. Функция у = √x и ее график. Вернуться к Списку уроков Тематического планирования.
Цель: рассмотреть функцию у = √х, ее свойства и график.
Планируемые результаты: знать основные свойства и график функции у = √х.
Тип уроков: уроки–практикумы.
Ход уроков
I. Сообщение темы и цели уроков
II. Работа по теме уроков
Пример 1
Пусть длина стороны квадрата равна а (см), а его площадь — S (см2). Величины S и а связаны соотношением S = а2 (где а ≠ 0). Это равенство означает, что каждому значению стороны квадрата а соответствует единственное значение его площади S. Из равенства S = а2 найдем а = √S. Такое соотношение означает, что для каждого значения площади квадрата S можно указать единственное значение его стороны а. Формулами S = а2 (где а ≥ 0) и а = √S задаются функциональные зависимости между одними и теми же переменными а и S. Однако в первом случае независимой переменной (аргументом) является сторона квадрата а, зависимой переменной (значением функции) — его площадь S. Во втором случае, наоборот, независимой переменной (аргументом) является площадь квадрата S, зависимой переменной (значением функции) — его сторона а. Заметим, что функции S = а2 (где а ≥ 0) и а = √S являются взаимообратными.
Пример 2
Если в предыдущем примере в каждом случае обозначить, как принято, независимую переменную буквой л:, а зависимую переменную — буквой у, то получим взаимообратные функции у = x2 (где х ≥ 0) и у = √х. Сравним свойства и графики этих функций.
Сначала составим таблицу значений функции у = √х и построим ее график.

Приведем основные свойства функции у = √х.
- Область определения функции — значения х ≥ 0.
- Область изменения (значений) функции — значения у ≥ 0.
- График функции пересекает оси координат в начале системы координат.
- Значения функции у ≥ 0 при х ≥ 0, и график расположен в первой координатной четверти.
- Функция монотонно возрастает.
Дадим определение монотонной функции. Пусть числа х1 и x2 принадлежат области определения функции и значения функции в этих точках у1 и у2 соответственно. Пусть (для определенности) x2 > х1. Если при этом для всех таких значений х1 и x2:
- у2 > у1 (т. е. большему значению аргумента соответствует большее значение функции), то функция возрастает (график идет вверх);
- у2 < у1 (т. е. большему значению аргумента соответствует меньшее значение функции), то функция убывает (график идет вниз).

Функция у = x2, ее свойства и график были изучены в 7 классе. Напомним основные свойства этой функции при х ≥ 0.
- Область определения функции — значения х ≥ 0.
- Область изменения (значений) функции — значения у ≥ 0.
- График функции пересекает оси координат в начале системы координат.
- Значения функции у ≥ 0 при х ≥ 0, и график расположен в первой координатной четверти.
- Функция монотонно возрастает.

Заметим, что графики функций у = √х и у = x2 (где х ≥ 0) симметричны относительно прямой у = х (биссектрисы первого и третьего координатных углов). Доказательства этого факта, а также свойства взаимообратных функций мы в 8 классе приводить не будем.

Пример 3
Для линейной функции у = 3х – 2 найдем обратную, построим графики этих функций и убедимся, что они симметричны относительной прямой у = х.
Переменные у и х связаны соотношением у = 3х – 2, что позволяет для любого значения х вычислить соответствующее значение у. Теперь из того же соотношения у = 3х – 2 выразим х: 3х = у + 2 и х = у/3 + 2/3. Теперь можно по любому значению у найти соответствующее ему значение у, т. е. х является функцией у. Так как принято независимую переменную обозначать буквой х, а зависимую — буквой у, то в выражении х = у/3 + 2/3 поменяем х на у, а у на х. Получаем функцию у = х/3 + 2/3. Эта функция является обратной для данной функции у = 3х – 2.

Видно, что эти графики симметричны относительной прямой у = х. На основании рисунка приведем еще некоторые свойства взаимообратных функций.
- Монотонность таких функций одинакова. Из рисунка видно, что обе функции возрастают.
- Если график данной функции пересекает ось абсцисс в точке х = а и ось ординат — в точке у = b, то график обратной функции, наоборот, пересекает ось абсцисс в точке х = b и ось ординат — в точке у = а. Из рисунка видно, что точки пересечения графика функции у = 3х – 2 с осями координат х = 2/3 и у = –2. Точки пересечения графика обратной функции у = х/3 + 2/3 с осями координат, наоборот, х = –2 и у = 2/3.
III. Задания на уроках
№ 352 (а); 355; 358 (а, б); 360; 362 (в); 363 (а, в, г); 365 (а, в).
IV. Контрольные вопросы
- Перечислите основные свойства функции у = √х и нарисуйте ее график.
- Перечислите основные свойства функции у = x2 (где х ≥ 0) и нарисуйте ее график.
- Приведите основные свойства взаимообратных функций. Что можно сказать о графиках таких функций?
V. Творческие задания

VI. Подведение итогов уроков
Домашнее задание: № 352 (б); 356; 358 (в, г); 361; 362 (б); 363 (б, д, е); 365 (б, г).
Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). Глава 2. КВАДРАТНЫЕ КОРНИ (19 ч). § 5. Арифметический квадратный корень (5 ч). Уроки 29, 30. Функция у = √x и ее график.
Вернуться к Списку уроков Тематического планирования.
Источник
Республика Татарстан, Черемшанский район, с. Черемшан
МБОУ «Черемшанский лицей»
Тема урока: «Функция у = √х, ее свойства и график»
Сахабиева Эльвира Маратовна
Учитель математики
МБОУ «Черемшанский лицей»,
с. Черемшан
2015-2016 г.
Функция у = √х, ее свойства и график
Тип урока: Урок по ознакомлению с новым материалом.
Вид урока: комбинированный.
Класс: 8
Цель урока:
- Изучить график и свойства функции у =
Задачи:
Образовательные
- Закрепить умения находить значения выражений, содержащих корень квадратный.
- Учить анализировать и находить правильное решение проблемной ситуации.
Воспитательные
- Воспитывать познавательную активность, чувство ответственности, культуру математической речи, графической культуры, сознательное отношение к учению.
Развивающие
- Развивать логическое мышление, наблюдательность, графические навыки.
Оборудование к уроку: Презентация Power Point
УМК: Алгебра 8 класс, Ю.Н.Макарычев, Н.Г. Миндюк,К. И. Нешков, С.Б. Суворова,2-е изд.-М.: Просвещение,2014.-287с.
Ход урока
- Организационный момент
Слайд 1.Приветствие учащихся, Девиз урока…Математику уже затем учить надо, что она ум в порядок приводит…М.В.Ломоносов
- Актуализация опорных знаний.
Фронтальная работа с классом:
Слайд 2.1). Ребята, а давайте вспомним определение арифметического квадратного корня (Ариф.квадратным корнем из числа а наз-ся неотрицательное число, квадрат которого равен а)
Значит важное условие здесь а>0
2) Устная работа
Слайд 3. а) Верно ли, что: = 0,3; (Ответ учащихся: да) = 0,5; (Ответ учащихся: нет) = 4?
(Ответ учащихся: нет), (Ответ учащихся: да)
Слайд 4. б) Выберите иррациональное число среди чисел ; (=0,8 рациональное число и т.д.)
(Это нужно прорешать у доски)
Слайд 5.в) Вычислите:
=7 ; нет решения. =
3. Обобщение и систематизация знаний. (С места по желанию)
Слайд 6. А теперь вычислим площадь квадрата со стороной, равной
Вспомним чему равна площадь квадрата?( , S= . =18)
Здесь вычислите площадь прямоугольника со сторонами и
Вспомним площадь прямоугольника (S=a*b, S= . =14*5=70)
Вычислим площадь прямоугольного треугольника, катеты которого
4. Проверка знаний и умений учащихся для подготовки к новой теме.
Слайд 7. Ребята посмотрите пожалуйста на формулы.
Кто помнит название этой функции. (линейная, квадратичная).
Вспомним что является графиком этой функции? (прямая и парабола)
Назовите независимые переменные (они находятся внутри формулы), а зависимые переменные (они находятсяся отдельно)?
Слайд 8. – Сегодня мы с вами рассмотрим новую функцию у =
(Давайте определим независимую переменную и зависимую переменную и какие значения они принимают?)
Слайд 9.- Тема урока: Функция у = , её свойства и график.
Слайд 10. Цель урока:- Мы должны изучить свойства и график функции у = .
Слайд.11. Для этого определим несколько значений этой функции и построим таблицу.
Соединим точки плавной линией (рука идет слева направо)
Слайд 12. Посмотрите через какие точки проходит график?
В каких четвертях будет расположен график функции у = ?
График нужно рассматривать слева направо, график идет вверх, значит функция возрастает.
5.Закрепление знаний
Слайд 13.
Устно найти значение функций на слайде
№355 (Пользуясь графиком в учебнике на стр.85 рис.17 найти значение и составить таблицу)
а)
б)
6. Физминутка.
Слайд 14. Потрудились – отдохнем,
Встанем – глубоко вздохнем.
Руки в стороны. вперед.
влево, вправо. поворот.
Три наклона, прямо встать,
Руки вниз, затем поднять,
Руки плавно опустили, всем улыбку подарили.
7.Работа с учебником, выполнение № 357,№363
8. Домашнее задание
Слайд 15. п. 15, №356, №364
9. Рефлексия.
Слайд 16.
- Сегодня на уроке я узнал…
- Сегодня на уроке я понял…
- Находить ответы на возникающие вопросы мне было…
10. Выставление оценок.
Слайд 17. Оцени себя , ,,,,
Источник
Êîðíåì n-ñòåïåíè èç íåîòðèöàòåëüíîãî ÷èñëà a ÿâëÿåòñÿ òàêîå íåîòðèöàòåëüíîå ÷èñëî, ïðè âîçâåäåíèè â n-ñòåïåíü êîòîðîãî ïîëó÷àåòñÿ ÷èñëî a.
Êîðíåì íå÷åòíîé n-ñòåïåíè èç îòðèöàòåëüíîãî ÷èñëà a íàçûâàåòñÿ òàêîå îòðèöàòåëüíîå ÷èñëî, ïðè âîçâåäåíèè â n-ñòåïåíü êîòîðîãî ïîëó÷àåòñÿ ÷èñëî a.
Ãäå n – ýòî ïîêàçàòåëü êîðíÿ è a – ïîäêîðåííîå ÷èñëî.
Òàêèì îáðàçîì, èçâëå÷ü êîðåíü ëþáîé ñòåïåíè (îò âòîðîé è äàëåå) ìîæíî èç ëþáîãî íåîòðèöàòåëüíîãî ÷èñëà, à èç îòðèöàòåëüíîãî ÷èñëà èçâëåêàåòñÿ òîëüêî êîðåíü íå÷åòíîé ñòåïåíè.
Íà [0; +∞) ìîæíî ïîñòàâèòü êàæäîìó ÷èñëó õ â ñîîòâåòñòâèå åäèíñòâåííîå ÷èñëî êîðåíü n-ñòåïåíè èç x ïðè ëþáîì çíà÷åíèè n.
Òî åñòü ýòî îçíà÷àåò, ÷òî íà ìíîæåñòâå [0; +∞) ìîæíî ãîâîðèòü î ôóíêöèè êîðíÿ:
Òåïåðü îïðåäåëèì ñâîéñòâà äàííîé ôóíêöèè è ïîñòðîèì åå ãðàôèê.
Îñíîâíûå ñâîéñòâà ôóíêöèè:
Ïðîìåæóòîê [0; +∞) – ÿâëÿåòñÿ îáëàñòüþ îïðåäåëåíèÿ.
Òàê êàê íåîòðèöàòåëüíîå ÷èñëî ÿâëÿåòñÿ êîðíåì n-ñòåïåíè èç íåîòðèöàòåëüíîãî ÷èñëà, çíà÷èò ïðîìåæóòîê [0; +∞) áóäåò îáëàñòüþ çíà÷åíèÿ ôóíêöèè.
Ïîñêîëüêó ñèììåòðè÷íûì ìíîæåñòâîì íå ÿâëÿåòñÿ îáëàñòü îïðåäåëåíèÿ ôóíêöèè, ïîýòîìó äàííàÿ ôóíêöèÿ íå ÿâëÿåòñÿ íè íå÷åòíîé, íè ÷åòíîé.
Îïåðàöèÿ ïî èçâëå÷åíèþ êîðíÿ ââîäèëàñü êàê îáðàòíàÿ îïåðàöèÿ âîçâåäåíèÿ â ñîîòâåòñòâóþùóþ ñòåïåíü.
Çíà÷èò ìîæíî óòâåðæäàòü, ÷òî:
Òåïåðü ìîæíî ïîñòðîèòü ãðàôèê ôóíêöèè êîðíÿ.

Ïîëüçóÿñü ãðàôèêîì, ìîæíî çàïèñàòü îñòàâøèåñÿ ñâîéñòâà ôóíêöèè.
Íà ïðîìåæóòêå [0; +∞) ôóíêöèÿ âîçðàñòàåò.
Ñâåðõó ôóíêöèÿ íå îãðàíè÷åíà, íî îíà îãðàíè÷åíà ñíèçó, íàïðèìåð, ïðÿìîé ó, êîòîðàÿ = -0,5.
Íà âñåé îáëàñòè îïðåäåëåíèÿ ôóíêöèÿ âûïóêëà ââåðõ.
Ó ôóíêöèè íàèìåíüøèì çíà÷åíèåì áóäåò ÿâëÿòüñÿ 0, à íàèáîëüøåãî çíà÷åíèÿ îíà íå èìååò.
Åñëè â êàæäîé èç òî÷åê íåêîòîðîãî ïðîìåæóòêà ôóíêöèÿ äèôôåðåíöèðóåìà, òî ýòî çíà÷èò, ÷òî íà äàííîì ïðîìåæóòêå îíà íåïðåðûâíà.
Òîãäà:
 ëþáîé òî÷êå ïðîìåæóòêà [0; +∞) ñóùåñòâóåò ýòà ïðîèçâîäíàÿ, èñêëþ÷åíèåì ÿâëÿåòñÿ òîëüêî òî÷êà 0. Ïîñêîëüêó â ëþáîé òî÷êå ïðîìåæóòêà (0; +∞) ôóíêöèÿ èìååò ïðîèçâîäíóþ, çíà÷èò íà ïðîìåæóòêå (0; +∞) ôóíêöèÿ äèôôåðåíöèðóåìà.
Ðàññìîòðèì íåñêîëüêî ïðèìåðîâ ãðàôèêîâ ôóíêöèè êîðíÿ.


Ýòè ïðèìåðû êàñàþòñÿ ôóíêöèè, ó êîòîðîé ó ðàâíî êîðåíü n-ñòåïåíè èç x, òîëüêî ïðè íåîòðèöàòåëüíûõ çíà÷åíèÿõ àðãóìåíòà.
Íî åñëè n ÿâëÿåòñÿ íå÷åòíûì ÷èñëîì, òî äëÿ îòðèöàòåëüíûõ õ òàêæå èìååò ñìûñë âûðàæåíèå êîðåíü n-ñòåïåíè èç x. À çíà÷èò, ãîâîðèòü ìîæíî î ôóíêöèè:
Çàïèøåì ñâîéñòâà äàííîé ôóíêöèè.
Ïðîìåæóòîê (– ∞; + ∞) ÿâëÿåòñÿ îáëàñòüþ îïðåäåëåíèÿ ôóíêöèè.
Ïðîìåæóòîê (– ∞; + ∞) áóäåò îáëàñòüþ çíà÷åíèé.
Îáëàñòü îïðåäåëåíèÿ ôóíêöèè ÿâëÿåòñÿ ñèììåòðè÷íûì ìíîæåñòâîì, çíà÷èò äàííóþ ôóíêöèþ ìîæíî èññëåäîâàòü íà ÷åòíîñòü:
Òàêèì îáðàçîì ïîëó÷àåì, ÷òî ôóíêöèÿ áóäåò íå÷åòíîé ïðè íå÷åòíîì n.
Ïîñòðîèì ãðàôèê ôóíêöèè.

Äîáàâèì ê ýòîé âåòâè åùå âåòâü, êîòîðàÿ ñèììåòðè÷íà åé îòíîñèòåëüíî íà÷àëà êîîðäèíàò, äëÿ ýòîãî âîñïîëüçóåìñÿ ñâîéñòâîì íå÷åòíîñòè ôóíêöèè êîðíÿ.

- Ïîëó÷èâøèéñÿ ãðàôèê ïîçâîëÿåò ëåãêî çàïèñàòü îñòàâøèåñÿ ñâîéñòâà ôóíêöèè.
- Íà âñåé îáëàñòè îïðåäåëåíèÿ ôóíêöèÿ âîçðàñòàåò.
- Íè ñâåðõó, íè ñíèçó ôóíêöèÿ íå îãðàíè÷åíà.
- Ó ôóíêöèè íåò íàèáîëüøåãî è íàèìåíüøåãî çíà÷åíèÿ.
- Íà âñåé îáëàñòè îïðåäåëåíèÿ ôóíêöèÿ íåïðåðûâíà.
- Íà ïðîìåæóòêå (– ∞; 0) ôóíêöèÿ âûïóêëà âíèç, à íà ïðîìåæóòêå (0; + ∞) îíà âûïóêëà ââåðõ.
- Íà âñåé îáëàñòè îïðåäåëåíèÿ ôóíêöèÿ äèôôåðåíöèðóåìà, çà èñêëþ÷åíèåì òî÷êè 0.
Åùå íåñêîëüêî ïðèìåðîâ ãðàôèêîâ ôóíêöèè êîðíÿ.



Источник
