Длина это какое свойство
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 декабря 2019;
проверки требует 1 правка.
Измерения:
L — длина,
B — ширина,
H — высота, толщина, глубина
Длина — физическая величина, числовая характеристика протяжённости линий.
В большинстве систем измерений единица длины — одна из основных единиц измерения, через которые определяются другие (производные) единицы. В международной системе единиц (СИ) за единицу длины принят метр.
В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).
В физике термин «длина» обычно используется как синоним «расстояния» и обозначается или от нем. länge (длина). Символ размерности длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная.
Единицы измерения длины[править | править код]
Метрическая система[править | править код]
Метрическая система считается[кем?] самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Международном бюро мер и весов, расположенном в городе Севр (предместье Парижа, Франция). Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.
Британская/американская система[править | править код]
Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.
- Лига (лье)
- Фурлонг
- Чейн
- Род
- Линк
- Ладонь
- Линия
Старорусская система[править | править код]
В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие[1].
В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.[2]
Относительные размеры
объектов, м
-20 —
–
-18 —
–
-16 —
–
-14 —
–
-12 —
–
-10 —
–
-8 —
–
-6 —
–
-4 —
–
-2 —
–
0 —
–
2 —
–
4 —
–
6 —
–
8 —
–
10 —
–
12 —
–
14 —
–
16 —
–
18 —
–
20 —
–
22 —
–
24 —
–
26 —
–
28 —
–
30 —
См. также[править | править код]
- Миля
- Межевая верста
- Верста
- Косая сажень
- Маховая сажень
- Пядь
Древнегреческая система[править | править код]
- Дактиль (единица измерения)
- Кондилос
- Оргия
- Палайста
- Пекис
- Плетр
- Подес
- Стадий, или «стадия»
- Эпидама
Мусульманская система[править | править код]
- Ангушт или Асба (аналог дюйма)
- Пай (аналог фута)
- Ба или кама, равная приблизительно 2 м
- Касаба или наб
- Фарсах или парасанг, равный трём милям по 1000 Ба, или 6 км
- Барид, равный четырём фарсахам[3]
Типографическая система[править | править код]
- Цицеро
- Пункт
Морская система[править | править код]
Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Её численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.
Международная морская миля составляет 1852 м, в отличие от морской мили британской системы (1853,184 м).
Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м)[4].
Единицы, применяемые в астрономии[править | править код]
- Астрономическая единица
- Световой год
- Парсек
Средства измерений длины, расстояния[править | править код]
Измерительные инструменты и меры[править | править код]
- Линейка
- Курвиметр
- Концевая мера
- Штангенинструмент
- Рулетка (инструмент)
- Микрометр (инструмент)
- Индикатор часового типа
- Калибр (инструмент)
- Толщиномер
Измерительные приборы[править | править код]
- Высотомер
- Радиовысотомер
- Дальномер
- Радиодальномер
- Интерференционные толщиномеры (ультразвуковые, лазерные, радиационные)
Другие средства[править | править код]
- Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
- Очень маленькие расстояния измеряются с помощью измерительных микроскопов
Расстояния и размеры объектов, доступных наблюдению[править | править код]
Основной источник: [5]
См. также[править | править код]
- Длина кривой
- Ширина
- Высота
- Глубина
- Мера
- Объём
- Площадь
Примечания[править | править код]
Источник
В геометрии длина – это величина, характеризующая протяженность отрезка.
Определение. Длиной отрезка называется неотрицательная величина, обладающая следующими свойствами:
1) равные отрезки имеют равные длины;
2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины, такой единицей является длина произвольного отрезка. Результатом измерения длины отрезка х является неотрицательное действительное число, обозначим его т(х). Это число называют численным значением длины отрезка х при выбранной единице длины или просто длиной.
Такое число всегда существует и единственно. Для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Из определения длины отрезка следуют известные свойства численных значений длин. Сформулируем некоторые из них, считая, что единица длины выбрана.
1. Если два отрезка равны, то численные значения их длин также равны, и обратно: если численные значения длин двух отрезков равны, то равны и сами отрезки.
х = y <=> т(х) = т(у)
2. Если отрезок х состоит из отрезков х, и х2, то численное значение его длины равно сумме численных значений длин отрезков х, и х2. Справедливо и обратное утверждение.
х = х1 х2 <=> т(х) = т(х1) + т(х2)
3. При замене единицы длины численное значение длины увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единицы.
Рассмотрим процесс измерение длин отрезков. Из множество отрезков выбирают какой – нибудь отрезок е и принимают его за единицу длины. На отрезке а от одного из его концов откладывают последовательно отрезки, равные е, до тех пор, пока это возможно. Если отрезки, равные е отложились п раз и конец последнего совпал с концом отрезка а, то говорят, что значение длины отрезка а есть натуральное число п, и пишут а = пе. Если же отрезки, равные е, отложились п раз и остался еще остаток, меньшее, то на нем откладывают отрезки равные е1= 1/10 ∙е. Если они отложились точно п1 раз, то тогда а = п1е и значение длины отрезка а есть конечная десятичная дробь. Если же отрезок е1отложился п1 раз и остался еще остаток, меньшей е1, то на нем откладывают отрезки равные е2 = 1/100 ∙ е. Если представить этот процесс бесконечно продолжительным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь.
Итак, при выбранной единицы длина любого отрезка выражается положительными числами.
На практике для измерения длин отрезков используются различные инструменты, в частности линейка с нанесенными на ней единицами длины.
При решении практических задач используются стандартные единицы длины: миллиметр (мм), сантиметр (см), метр (м), километр (км) и др.
Соотношение между ними:
1 километр (км) = 1000 метрам (м)
1 метр (м) = 10 дециметрам (дм) = 100 сантиметрам (см)
1 дециметр (дм) = 10 сантиметрам (см)
1 сантиметр (см) = 10 миллиметрам (мм)
Дата добавления: 2015-04-18; просмотров: 385; Нарушение авторских прав
Источник
Лекция 10. Длина отрезка и её измерение.
Понятие длины отрезка и ее измерения используется во многих областях деятельности человека и научных исследованиях. Поэтому рассмотрим эту величину более детально.
Определение. Длиной отрезка называется положительная величина, определенная для каждого отрезка, так, что: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков.
Процесс измерения длины отрезков выглядит так. Из множества отрезков выбирают какой-нибудь отрезок е и принимают его за единицу длины. На отрезке а, длину которого измеряют, от одного из его концов откладывают последовательно отрезки, равные е, до тек пор, пока это возможно. Если отрезки, равные е, отложились n раз и конец последнего отрезка совпал с концом отрезка а, то говорят, что значение длины отрезка а есть натуральное число n и пишут а = n е. Если же отрезки, равные е, отложились n раз, и еще остался остаток, меньший е, то на нем откладывают отрезки, равные е1 = 110 е. Если они отложились ровно n1раз, то тогда а = n, n1 е, и значение длины отрезка есть конечная десятичная дробь. Если же отрезок е1 отложился n1 раз и остался еще остаток, меньший е1, то на нем откладывают отрезки, равные е2= 1100е1. Если представить этот процесс бесконечно продолженным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь. Таким образом, при выбранной единице длины длина любого отрезка выражается положительным действующим числом. Вполне очевидно, что верно и обратное: если дано положительное действительное число, то всегда можно построить отрезок, численное значение которого выражается этим действительным числом.
Нетрудно доказать следующие свойства длин отрезков.
1. При выбранной единице длины длина любого отрезка выражается положительным действительным числом и для каждого положительного действительного числа есть отрезок, длина которого выражается этим числом.
2. Если два отрезка равны, то и численные значения их длин также равны, и обратно: если численные значения длин отрезков равны, то и равны сами отрезки, т.е. а = в mе (а) = mе (в).
3. Если данный отрезок равен сумме нескольких отрезков, то численное значение его длины равно сумме численных значений длин отрезков слагаемых и, обратно, если численное значение длины отрезка равно сумме численных значений отрезков слагаемых, то и сам отрезок равен сумме этих отрезков, т.е. с = а + в mе (с) = mе (а) + mе (в).
4. Если длины отрезков а и в таковы, что в = х ∙ а, где х – положительное действительное число и длина отрезка а измерена при помощи единицы измерения е, то, чтобы найти численное значение отрезка в при единице измерения е, достаточно число х умножить на численное значение длины отрезка а при единице измерения е, т.е. в = х а mе (в) = х mе (а).
5. При замене единицы измерения длины численное значение длины отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица измерения длины отрезка меньше (больше) старой. Из других свойств длины отрезков отметим следующие.
6.а > в mе (а) >mе (в);
7.с = а – в mе (с) = mе (а) – mе (в);
8.х = а : в х = mе (а) : mе (в).
Все эти свойства позволяют сравнение длин отрезков и действия над ними сводить к сравнению и действием над соответствующими числовыми значениями длин этих отрезков. На практике, сравнивая длины отрезков и выполняя действия над длинами отрезков, теоретические положения, сформулированные выше, используются неявно.
Примеры.
1. 12 м < 12,3 м, так как 12 < 12,3.
2. 8,8 см + 3,4 см = (8,8 + 3,4) см = 12,2 см.
3. 18 ∙ 3 дм = (18 ∙ 3) дм = 54 дм.
Приводим несколько типичных задач.
Задача 1. Постройте отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза?
Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е. Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 20 равных частей, либо на 5, поскольку 0,2 = 15. Если от точки В отложить отрезок, равный 15 единичного, то длина отрезка АС будет равна 3,2Е.
Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим: 3,2 : 3 = 3 15 : 3 = 1615 = 1115.
Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1115.
Задача 2. Начертите два отрезка: длина первого – 8 см, а другой – в 2 раза длиннее. Чему равна длина второго отрезка?
Решение. 1 способ. Строят отрезок 6 см, а затем на луче ОА последовательно откладывают 2 равных отрезка длиной 6 см. Полученный отрезок ОА является искомым, его длина: 2 ∙ 6 (см) = 12 (см). 2 способ. Находят длину второго отрезка: 2 ∙ 6 (см) = 12 (см), а затем строят два отрезка: один – длиной 6 см, а другой – длиной 12 (см).
Задача 3. Отрезок длиной 18 см разделите на две равные части. Решение. Поскольку не выделена операция деления длины отрезка на натуральное число, то мы воспользуется тем, что деление на натуральное число равносильно умножению ее на дробь 1n. В связи с этим получаем: 18 (см) : 2 = 18 см ∙ 12 = 8 ∙12 см = 9 см. Ответ: 9 см.
В заключение приводим таблицу мер длины. 1 сантиметр (см) = 10 миллиметрам (мм); 1 дециметр (дм) = 10 сантиметрам (см); 1 метр (м) = 10 дециметрам (дм) = 100 сантиметрам (см); 1 километр (км) = 1000 метрам (м).
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Длина отрезка
Отрезок – это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.
Измерить отрезок – значит найти его длину(расстояние между его концами).
Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.
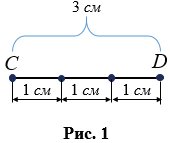
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.

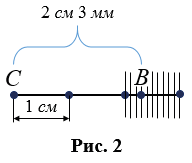
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:
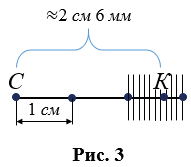
- Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.
За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.
Длина отрезка – это всегда какое-то положительное число.
Свойства длин отрезков:
- Равные отрезки имеют равные длины.
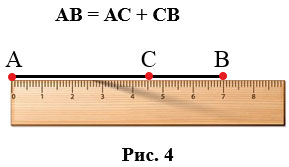
- Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.
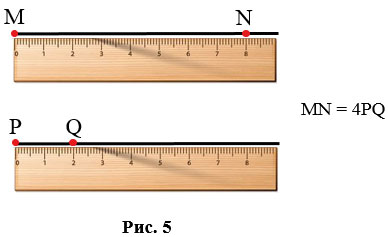
- Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записывают MN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 24,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 27,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 28,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 30,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 34,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 35,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 37,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 38,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 40,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
ДЛИНА́, -ы́, ж.
1. Протяжение линии, плоскости, тела в том направлении, в котором две крайние его точки наиболее удалены друг от друга. Меры длины. Измерить длину и ширину. || Расстояние между концами чего-л.; протяжение, протяженность. Длина отрезка прямой. Длина пути. Длина судоходного канала. □ Веревка была длиною почти во всю комнату. Пушкин, Дубровский. На окраине [города], по всей длине улицы, остановилась на ночь колонна грузовых машин. Первенцев, Огненная земля.
2. Продолжительность, длительность. Длина рабочего дня. Длина рассказа.
Источник (печатная версия): Словарь русского языка: В 4-х
т. / РАН,
Ин-т лингвистич.
исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.;
Полиграфресурсы,
1999;
(электронная версия): Фундаментальная
электронная
библиотека
- Длина — физическая величина, числовая характеристика протяжённости линий. В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).
В физике термин «длина» обычно используется как синоним «расстояния» и обозначается
L
{displaystyle L}
или
l
{displaystyle l}
от англ. length (длина).
Символ размерности длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная. В большинстве систем измерений единица длины — одна из основных единиц измерения, через которые определяются другие (производные) единицы. В международной системе единиц (СИ) за единицу длины принят метр.
Источник: Википедия
ДЛИНА’, ы́, мн. нет, ж. Протяжение линии, плоскости, тела в том направлении, в к-ром две крайние точки (линии, плоскости, тела) лежат на наибольшем расстоянии одна от другой. Предметы измеряются в длину, ширину и высоту. Д. стола. Меры длины (совокупность принятых единиц линейного измерения). || Протяжение пути вдоль чего-н. Д. окружности. Д. реки. Д. дороги. || перен. Длительность, величина. Д. романа.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940);
(электронная версия): Фундаментальная
электронная
библиотека
длина́
1. пространственное измерение, расстояние между максимально удаленными друг от друга концами протяжённого объекта ◆ Длина стола. Длина пути. ◆ Сперматозоид состоит из головки, шейки, тела и хвоста, общая длина ― около 50-60 мкм. Анна Варшавская, «Дар не случайный», 2002 г. // «Домовой» (цитата из НКРЯ) ◆ Представительницы сборной США заняли последние места сразу в трех дисциплинах (200 м, 1500 м и прыжки в длину), таким образом, вычеркнув свою команду из числа претенденток на Кубок мира. Сергей Подушкин, «Звезды континентов. Россиянки выиграли Кубок мира по легкой атлетике», 2002 г. // «Известия» (цитата из НКРЯ)
2. матем. протяжённость прямой, полученной из данной геометрической фигуры или линии путем ее вытягивания и распрямления ◆ Длина окружности. ◆ Если не хочется «возиться» с клеем, возьмите двусторонний скотч (около 50 рублей за штуку, длина 10 метров). Елена Волкова, «Тот самый линолеум», 2002 г. // «Биржа плюс свой дом (Н. Новгород)» (цитата из НКРЯ)
3. продолжительность, длительность (о времени). ◆ Может, Господь дал мне возможность восполнить пробел длиной в восемнадцать лет через Сашу, через моё с ней общение? Сати Спивакова, «Не всё», 2002 г. (цитата из НКРЯ) ◆ В цепочке чисел, выражающих длины царствований, не все числа одинаково информативны (в математическом смысле) А. А. Зализняк, «Лингвистика по А. Т. Фоменко», 2000 г. // «Вопросы языкознания» (цитата из НКРЯ) ◆ Наименее информативны числа, близкие к средней длине поколения ― около 25-30 лет. А. А. Зализняк, «Лингвистика по А. Т. Фоменко», 2000 г. // «Вопросы языкознания» (цитата из НКРЯ)
4. протяжение линии, плоскости, тела и т. п. в том направлении, в котором две крайние его точки наиболее удалены друг от друга ◆ Например, в модели River of Pink Sapphires у TAG Heuer розовые сапфиры «стекают» по всей длине стального браслета. Екатерина Блинова, «Время не имеет значения», 2002 г. // «Домовой» (цитата из НКРЯ) ◆ Несмотря на относительную сложность реализации, такой способ связи имеет свои преимущества: а) не требуется изменение микропрограммного обеспечения ЧПУ; б) скорость обмена информацией ограничена только скоростью её обработки в системе ЧПУ, поэтому управляющую ЭВМ можно рассматривать как быстродействующий накопитель большой ёмкости; в) в режиме работы с дозагрузкой управляющей программы снимается ограничение на длину последней; г) быстрая переналадка на другой тип протокола связи с ЧПУ посредством программной смены параметров передачи. В. Ф. Безъязычный, А. Ю. Татаринов, М. В. Тимофеев, «Проблемы внедрения CAD/CAM систем в промышленности // Автоматизация технологических процессов в машиностроении», 2002 г. // «Межвузовский сборник научных трудов» (цитата из НКРЯ) ◆ Если сверхдлинная строка (цепочка) знаков и является физическим объектом, то ― хотя бы начиная с некоторой длины ― объектом скорее мысленным, чем реальным. В. А. Успенский., «Витгенштейн и основания математики», 2002 г. (цитата из НКРЯ) ◆ В Америке объявили конкурс на лучший анекдот длиной в сто слов. «Коллекция анекдотов: анекдоты об анекдотах», 1970–2000 г. (цитата из НКРЯ)
Источник: Викисловарь
Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать
Карту слов. Я отлично
умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова ремиссия (существительное):
Понятия со словом «длина»
Прыжок в длину — дисциплина технических видов легкоатлетической программы, относящаяся к горизонтальным прыжкам. Прыжок в длину требует от спортсменов прыгучести, спринтерских качеств. Прыжок в длину входил в соревновательную программу античных Олимпийских игр. Является современной олимпийской дисциплиной лёгкой атлетики для мужчин с 1896 года и для женщин с 1948 года.
Концевая мера длины (КМД, меры концевые плоскопараллельные, плитки Иогансона) — образцовая мера длины (эталон) от 0,5 до 1000 мм, выполненная в форме прямоугольного параллелепипеда или круглого цилиндра, с нормируемым размером между измерительными плоскостями.
Длина кривой (или, что то же, длина дуги кривой) — числовая характеристика протяжённости этой кривой. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление).
Метод дисперсионной рентгеновской спектроскопии по длине волны (ДРСДВ) (англ. Wavelength dispersive X-ray spectroscopy, WDXRF или WDS) — аналитическая методика элементного анализа твёрдого вещества, базирующаяся на анализе максимумов по их расположению (длина волны эмиссии) и интенсивности её рентгеновского спектра, вариант рентгеноспектрального анализа. С помощью ДРСДВ-методики можно количественно и качественно определить элементы в исследуемом материале начиная с атомного номера 4 — (Бериллий…
- (все понятия)
Источник
